数据结构-----图(Graph)论必知必会知识
目录
前言
图的基本概念
1.什么是图?
2 .图的相关术语
3 .有向图和无向图
4.简单图和多重图
5.连通图、强连通图、非连通图
6.权与网
7.子图和(强)连通分量
8.生成树和生成森林
前言
今天我们学习一种新的数据结构-----图,大家在日常生活中经常都会跟“图”打交道,比如说地图,电路图等等……,那我们都会发现图都有一个共同特点,那就是图里面的路径是没有规律的,一个地点到另一个地点的路径是不唯一的,同样的在数据结构当中图也是这样子的,那下面就一起进入到图的学习当中吧~
图的基本概念
1.什么是图?
前面总结了“树”这种数据结构,而这篇博客总结的是更为复杂的一种数据结构:图(graph),它表明了物件与物件之间的“多对多”的一种复杂关系。图包含了两个基本元素:顶点(vertex, 简称V)和边(edge,简称E)。
定义:结点集合V={v1,v2,v3,v4……}和连接节点的边集合 E={e1,e2,e3,e4……}组成的二元组G=<V,E> 称作为图(graph)。图中节点集合的基数n称作为图的阶数(order)。图G<V,E>称作为n阶图或者(n,m)图。

2 .图的相关术语
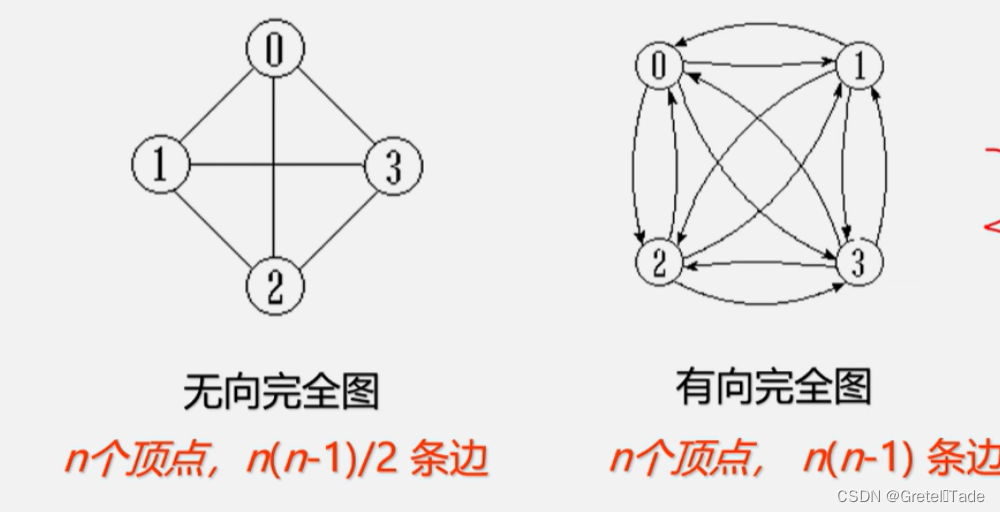
完全图: 任意两个点都有一条边相连
稀疏图: 有很少边或弧的图 (e<nlogn)
稠密图:有较多边或弧的图。
网:边/弧带权的图。
邻接:有边/弧相连的两个顶点之间的关系
存在(vi vj),则称vi和vj;互为邻接点;
存在<vi,vj>,则称vi邻接到vj, vi邻接于vj关联(依附): 边/弧与顶点之间的关系
存在(vi, vj)/ <vi, vj>, 则称该边/狐关联于vi和vj
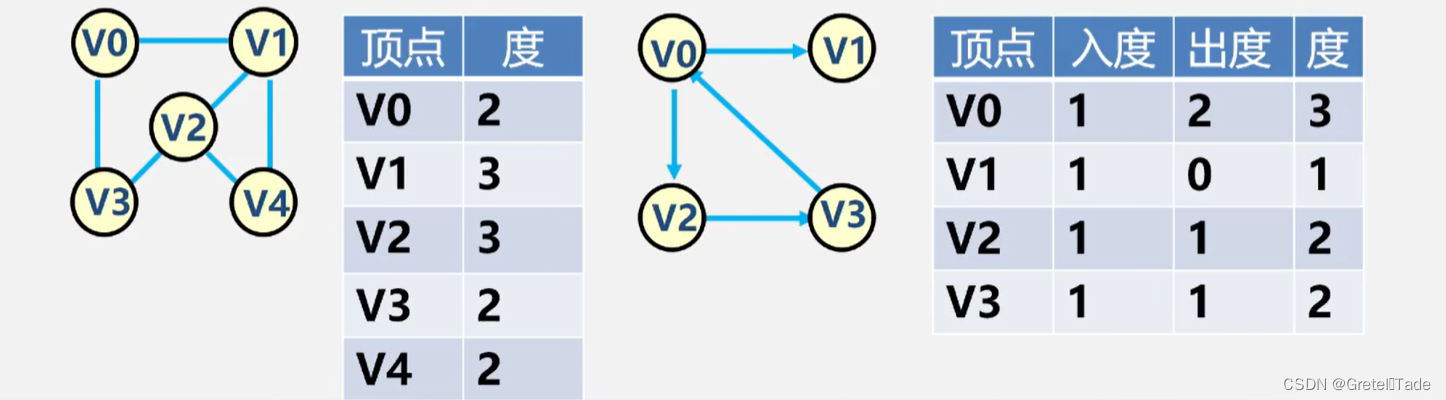
顶点的度: 与该顶点相关联的边的数目,记为TD(v)在有向图中,顶点的度等于该顶点的入度与出度之和。
顶点 v 的入度是以v 为终点的有向边的条数记作ID(v)
顶点 v 的出度是以 v 为始点的有向边的条数记作 OD(v)
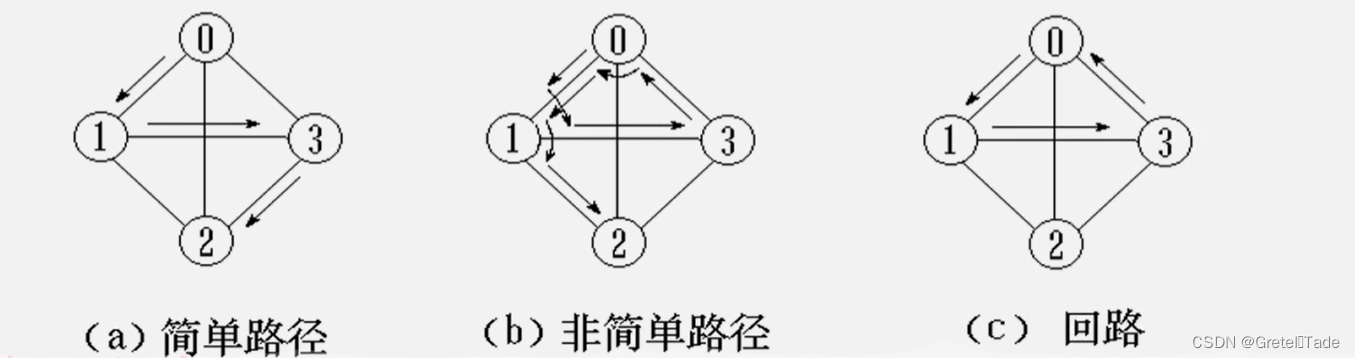
路径:接续的边构成的顶点序列。
路径长度: 路径上边或弧的数目/权值之和。回路(环): 第一个顶点和最后一个顶点相同的路径简单路径: 除路径起点和终点可以相同外,其余顶点均不相同的路径简单回路(简单环): 除路径起点和终点相同外,其余顶点均不相同的路径
3 .有向图和无向图
如果给图的每条边规定一个方向,那么得到的图称为有向图。在有向图中,从一个顶点出发的边数称为该点的出度,而指向一个顶点的边数称为该点的入度。相反,边没有方向的图称为无向图。
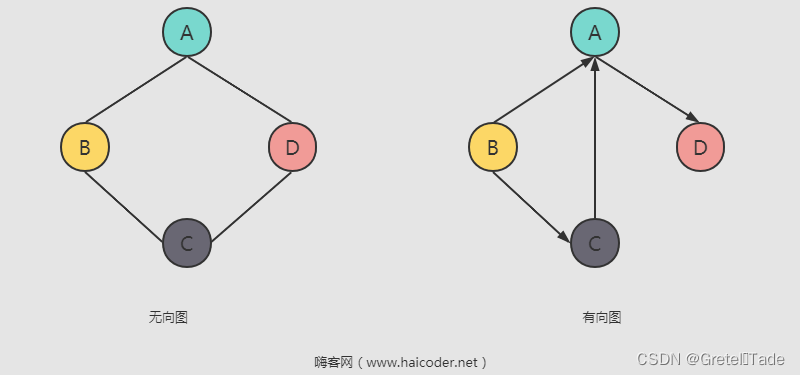
1.有向图的写法表示: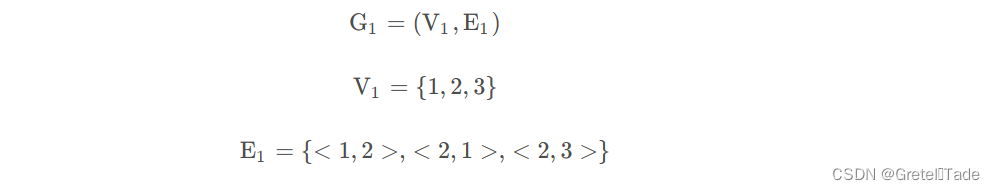
2.无向图的写法表示: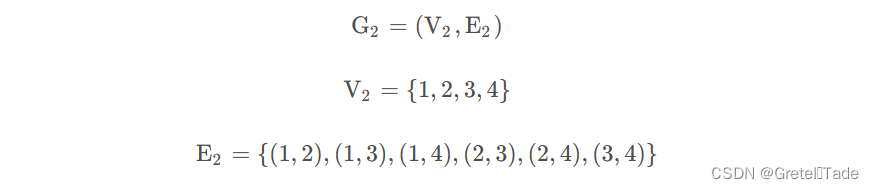
4.简单图和多重图
定义:含有平行边的图叫做多重图
既不含平行边,又不含有自换的图叫做简单图
多重图: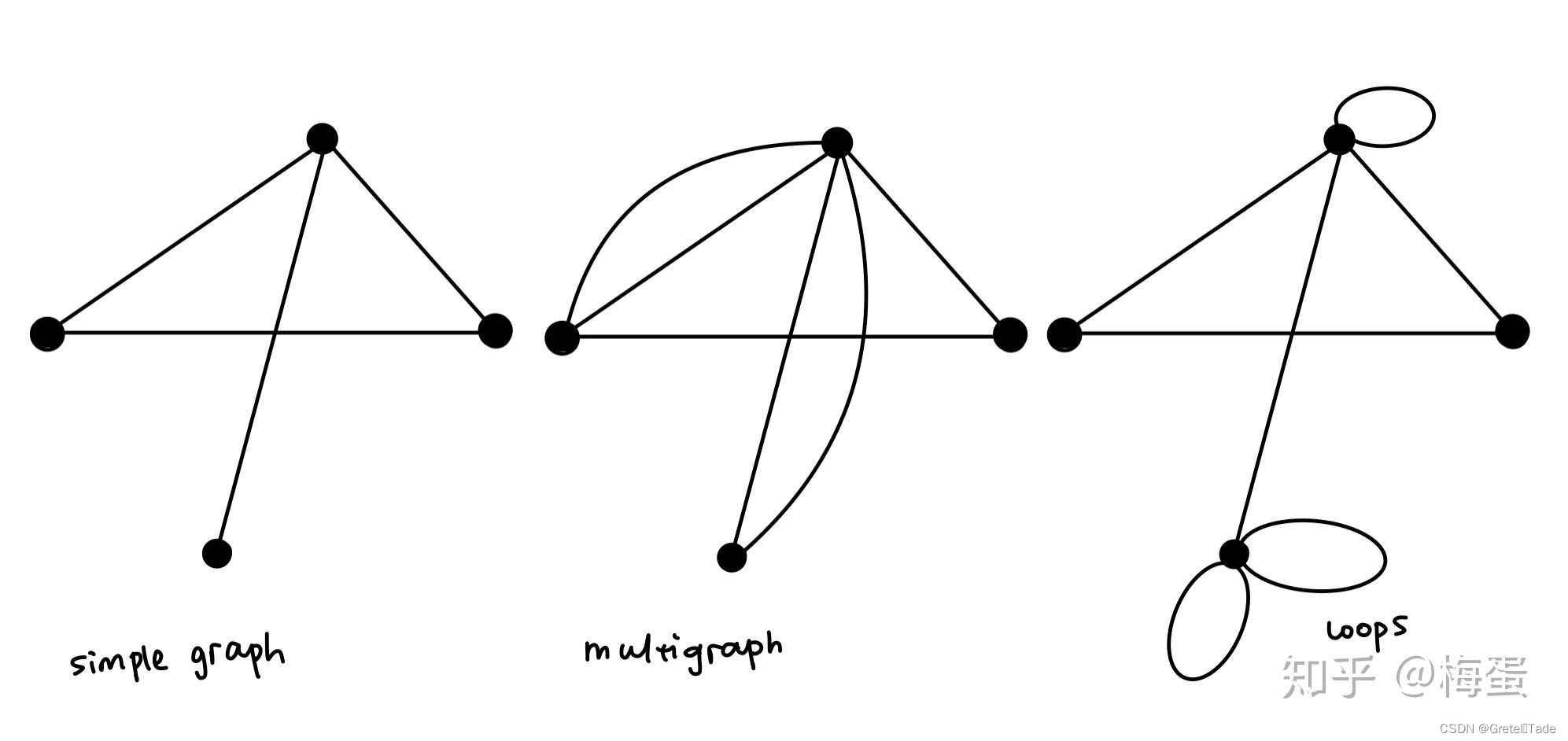 简单图:
简单图:
5.连通图、强连通图、非连通图
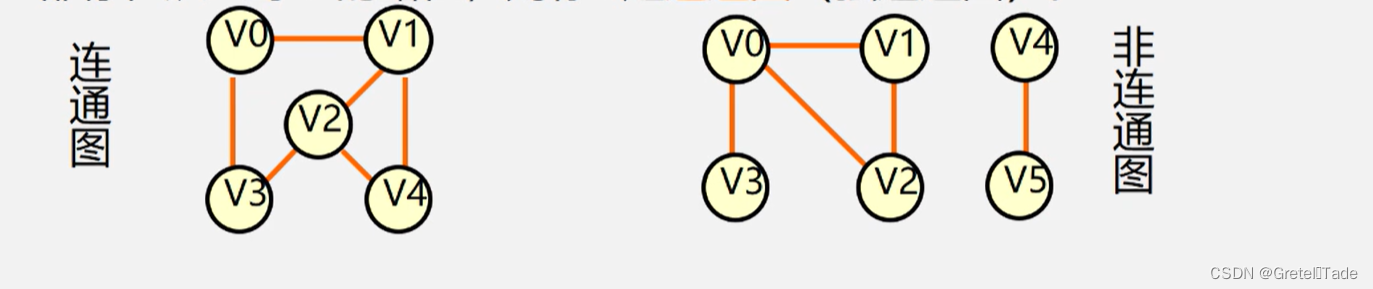
连通图:在无向图G=( V,E) )中,若对任何两个顶点 v、u都存在从v 到 u 的路径,则称G是连通图
强连通图:在有向图G=( V,E) )中,若对任何两个顶点 v、u都存在从v 到 u 的路径,则称G是强连通图
区分,无向图满足连通性,就叫做连通图,有向图叫做强连通图
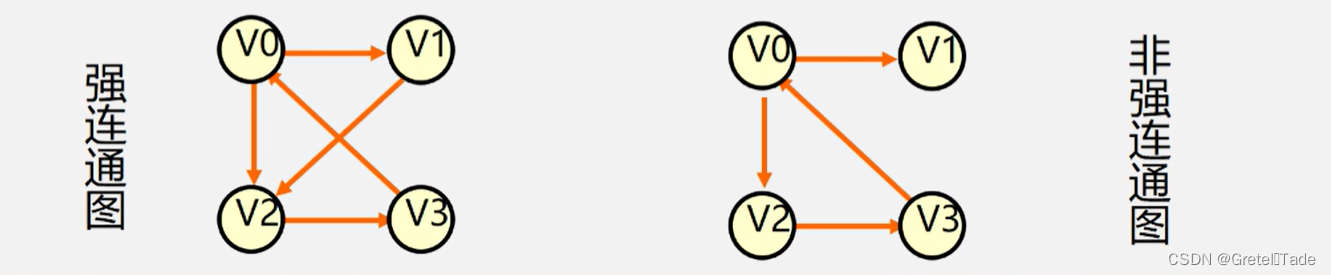
非连通图:跟连通图反过来,存在一个节点v无法到达另一个节点u的图,就称作为非连通图
6.权与网
权与网:
图中边或弧所具有的相关数称为权。表明从一个顶点到另一个顶点的距离或耗费
带权的图称为网
网,如图所示:
7.子图和(强)连通分量
子图:
下图中,b和c哪个是a的子图? 答案:c
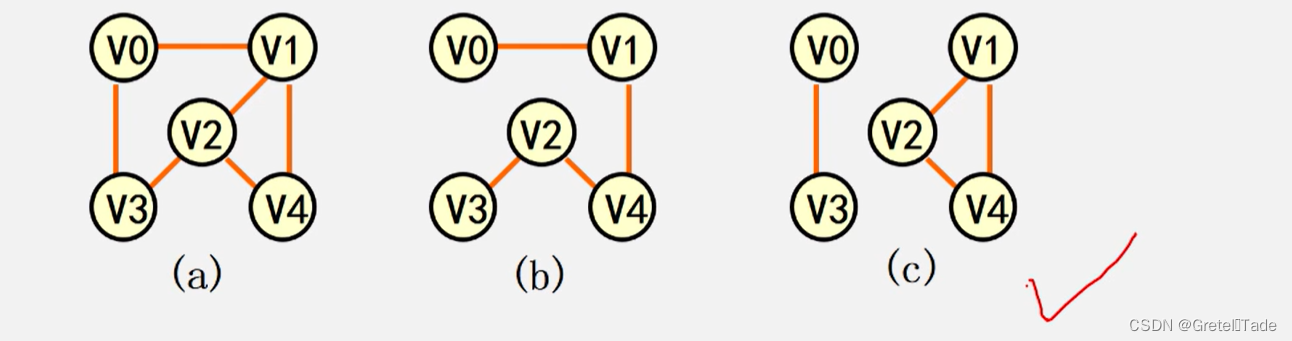
连通分量:无向图G 的极大连通子图称为G的连通分量
极大连通子图意思是: 该子图是 G 连通子图,将G 的任何不在该子图中的顶点加入,子图不再连通
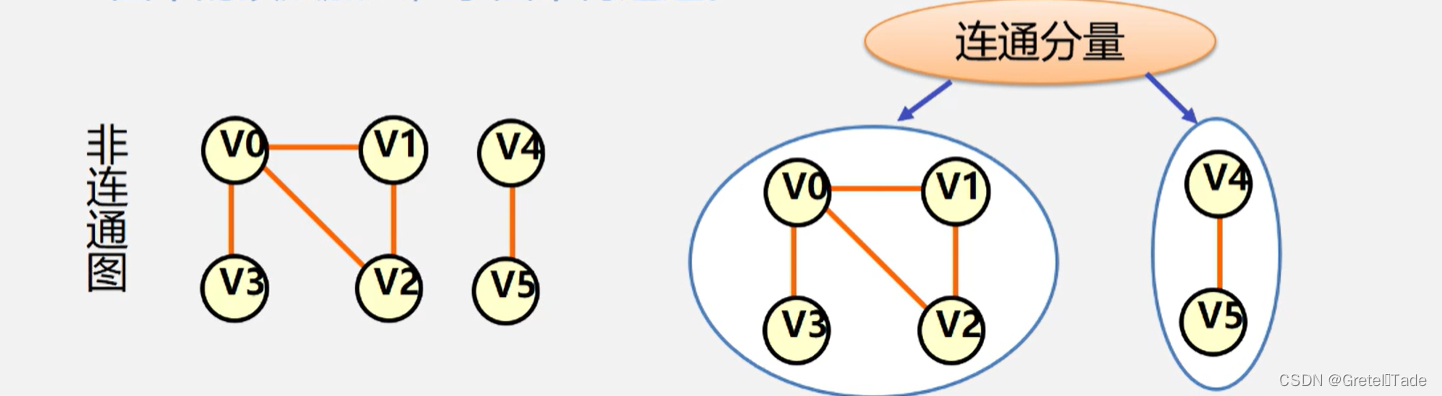
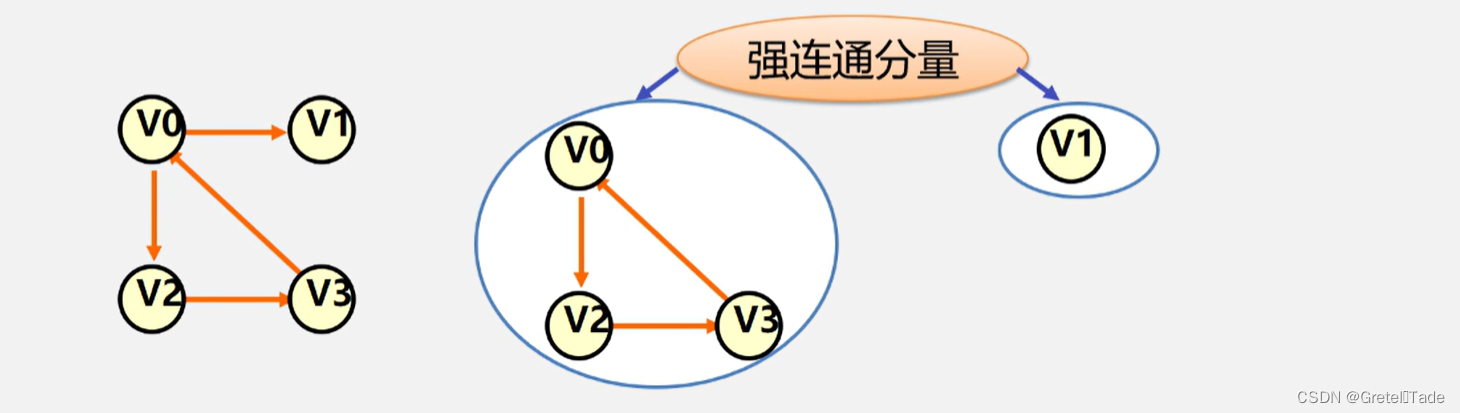
强连通分量:有向图G 的极大强连通子图称为G的强连通分量
极大强连通子图意思是: 该子图是G的强连通子图,将D的任何不在该子图中的顶点加入,子图不再是强连通的.
补充
极小连通子图:该子图是G 的连通子图,在该子图中删除任何一条边子图不再连通
8.生成树和生成森林
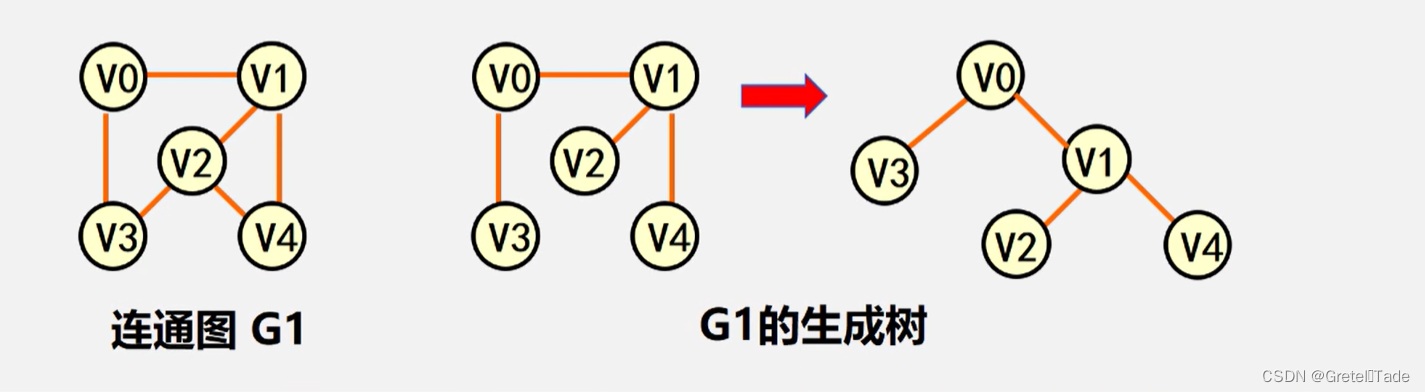
生成树:包含无向图G 所有顶点的极小连通子图
生成森林:对非连通图,由各个连通分量的生成树的集合
以上就是本期的全部内容了,如果你学过离散数学就都学过这些的,这些图论的知识点很重要的,一定要会哦!下一期我们就讲图的存储结构。
分享一张壁纸: 
相关文章:

数据结构-----图(Graph)论必知必会知识
目录 前言 图的基本概念 1.什么是图? 2 .图的相关术语 3 .有向图和无向图 4.简单图和多重图 5.连通图、强连通图、非连通图 6.权与网 7.子图和(强)连通分量 8.生成树和生成森林 前言 今天我们学习一种新的数据结构-----图,大家在日常生活中经常都…...

外汇天眼:法国金融市场管理局(AMF)致力于向零售投资者提供有关金融产品费用的信息
法国金融市场管理局(AMF)已经发布了一份专为专业人士准备的指南,以便他们使用更易于理解和比较的术语,以帮助客户更好地理解和比较费用。 AMF在其网站上推出了一个新的费用信息栏目,提供教育内容和工具,帮…...

【PythonGIS】基于Python批量合并矢量数据
老样子最近有项目需要将N个矢量文件合并成一个,总不能用ArcGIS一个个导入吧。所以我就想着用Python编个程序实现批量合并矢量。我之前也发了一些关于Python操作矢量数据的文章:【Python&GIS】Python处理矢量数据的基本操作(查询、修改、删…...

精益求精:使用Ansible集中式自动备份核心数据
1、引言 在当今数字化时代,数据是企业和组织的核心资产。为了确保数据的安全性和可恢复性,备份是至关重 要的。然而,手动备份数据可能会繁琐且容易出错,特别是在面对大规模和分布式的数据存储情况下。幸运的是,Ansibl…...

大数据高级面试题
大数据高级面试题 Kafka的producer如何实现幂等性? Producer 幂等性 Producer 的幂等性指的是当发送同一条消息时,数据在 Server 端只会被持久化一次,数据不丟不重,但是这里的幂等性是有条件的: 只能保证 Producer 在单个会话内…...

如何拦截响应内容并修改响应头
背景及需求描述 背景 记录分享下近期遇到并解决的困扰了比较久的问题:在不同系统微信生态发现同一个cos地址用window.open(url)打开在苹果和安卓设备的微信生态上表现不一致:对于文档类型,响应头Content-Type: application/pdf 在安卓微信上…...

分类预测 | Matlab实现WOA-GRU鲸鱼算法优化门控循环单元的数据多输入分类预测
分类预测 | Matlab实现WOA-GRU鲸鱼算法优化门控循环单元的数据多输入分类预测 目录 分类预测 | Matlab实现WOA-GRU鲸鱼算法优化门控循环单元的数据多输入分类预测分类效果基本描述程序设计参考资料 分类效果 基本描述 1.Matlab实现WOA-GRU鲸鱼算法优化门控循环单元的数据多输入…...

特定深度节点链表
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 经典BFS与简单链表结合的题目。 #define MAX_DEPTH (1000)struct ListNode** listOfDepth(struct TreeNode* tree, int* returnSize) {*returnSize 0;struct ListNode **ans (…...
【css】背景换颜色
更换前 longin.html <!DOCTYPE html> <html lang"en" > <head><meta charset"UTF-8"><title>login</title><link href"/css/style.css" type"text/css" rel"stylesheet"><s…...

什么是美颜sdk?直播实时美颜sdk的工作流程和架构分析
在现代社交媒体和娱乐行业中,直播已经成为了一种受欢迎的娱乐形式,同时实时美颜也变得越来越重要。直播实时美颜SDK的工作流程和架构在这一领域起到了关键作用。本文将深入探讨这些SDK的内部机制,从而理解它们如何为用户提供出色的美颜效果。…...

第二证券:跌破3000点,热搜第一!
今天上午,“沪指开盘跌破3000点关口”冲上百度热搜榜榜首。 上午收盘,上证指数下跌0.27%,报2997.22点;深证成指下跌0.36%,创业板指下跌0.44%。 赛道股发力,光伏、风电、新能源轿车等板块盘中冲高。房地产…...
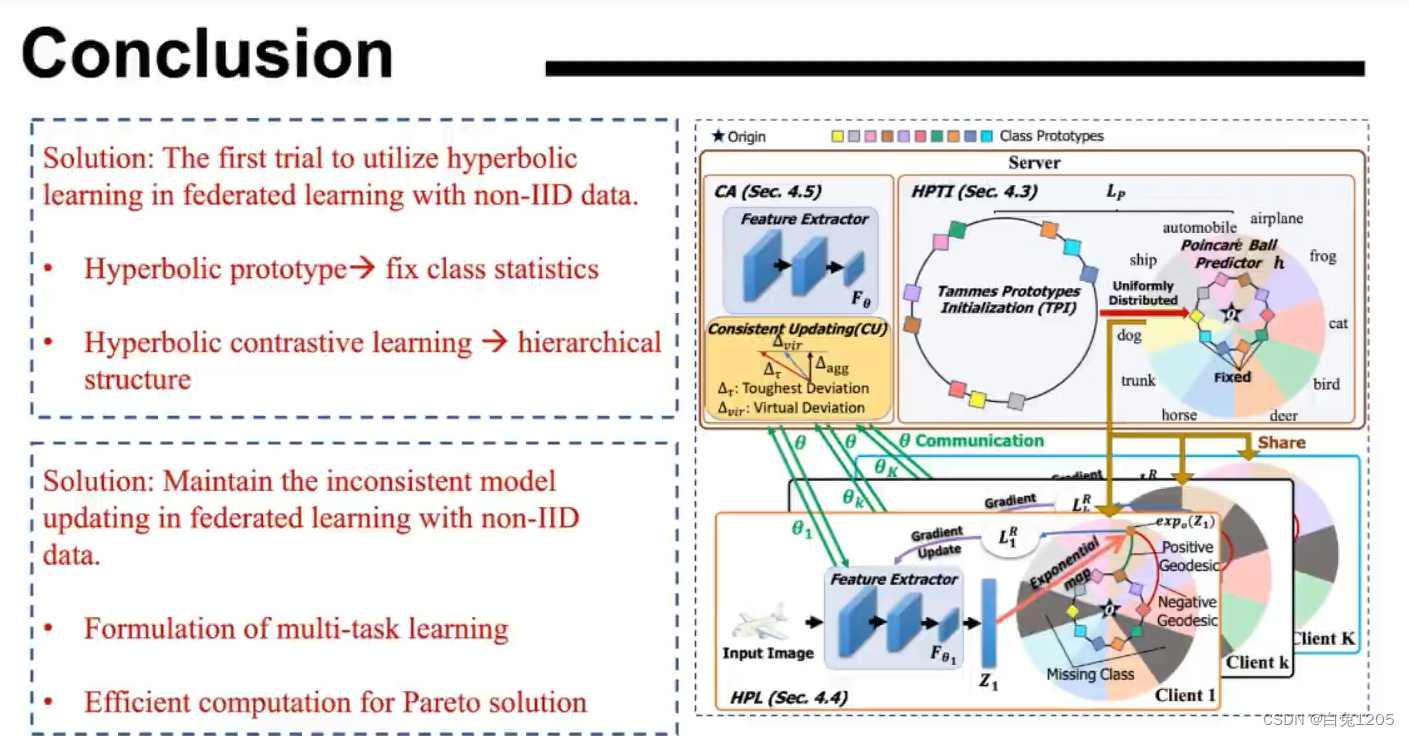
IJCAI2023【基于双曲空间探索的非独立同分布联邦学习】
1、介绍汇报的主题及汇报者 2、粗略介绍面临的挑战及出发点 3、介绍一下预备知识 4、解决方案 5、总览 6、实验设置 7、实验 8、结论...

实现Linux下Word转PDF、Java调用命令方式
使用 LibreOffice 实现 Word 转 PDF 和 Java 调用命令 1、 安装 LibreOffice 外网安装 # 一键安装 yum install -y libreoffice # 验证版本 libreoffice --version # Warning: -version is deprecated. Use --version instead. # LibreOffice 7.5.6.2 f654817fb68d6d4600d7…...
相关)
Java并发-06-AQS(AbstractQueuedSynchronizer)相关
1-概述 AQS全称是 AbstractQueuedSynchronizer,是阻塞式锁和相关的同步器工具的框架。同步器的设计是基于模板方法模式的,也就是说,使用者需要继承同步器并重写指定的方法,随后将同步器组合在自定义同步组件的实现中,并…...
【Python接口自动化】--深入了解HTTP接口基本组成和网页构建原理
引言 Python接口自动化有着广泛的应用场景,但是在实际使用过程中,可能会出现一些问题。比如,你不知道HTTP接口的基本构成,也不清楚网页是如何构建的。 这时,你就需要深入了解HTTP接口的基本组成和网页构建原理。通过本…...

window mysql5.7.27 启用SSL openssl mysql_ssl_rsa_setup
应客户监管部门要求 mysql必须要启用SSL。由于mysql安装在window上,启用过程中遇到了不少的坑,在此记录一下。 安装openssl 如果已经安装过可跳过此步 https://slproweb.com/download/Win64OpenSSL-1_1_1w.msi复制到浏览器下载后安装即可。如果需要其他…...
性能测试-JMeter分布式测试及其详细步骤
性能测试概要 性能测试是软件测试中的一种,它可以衡量系统的稳定性、扩展性、可靠性、速度和资源使用。它可以发现性能瓶颈,确保能满足业务需求。很多系统都需要做性能测试,如Web应用、数据库和操作系统等。 性能测试种类非常多,…...

学习gin-vue-admin之创建api和swagger
文章目录 go:generateViper 读写配置文件ZAP 保存日志定时任务创建apimodel步骤 1. 创建service步骤 2. 创建api步骤 3. 创建router 初始化总路由启动go-swagger路由配置swag init test将嵌套结构定义为指针或对象利弊结构体嵌套学习资源 go:generate //go:generate go env -w …...

2023-10-17 mysql-innodb-解析write_row的record的一行数据-分析
摘要: 2023-10-17 mysql-innodb-解析write_row的record的一行数据-分析. record是一行数据的序列化后的一整个字节流, 在innodb中需要解读出字段. 本文分析如何解析record, 以便学习这种技巧. row_mysql_store_col_in_innobase_format 调用堆栈: #0 row_mysql_store_col_in…...
认识web自动化测试!
1.什么是自动化测试? 自动化测试的概念: 软件自动化测试就是通过测试工具或者其他手段,按照测试人员的预定计划对软件产品进行自动化测试,他是软件测试的一个重要组成部分,能够完成许多手工测试无法完成或者难以实现的测试工作&a…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...