机器学习,神经网络中,自注意力跟卷积神经网络之间有什么样的差异或者关联?
如图 6.38a 所示,如果用自注意力来处理一张图像,假设红色框内的“1”是要考虑的像素,它会产生查询,其他像素产生

图 6.37 使用自注意力处理图像
键。在做内积的时候,考虑的不是一个小的范围,而是整张图像的信息。如图 6.38b 所示,在
做卷积神经网络的时候,卷积神经网络会“画”出一个感受野(receptive field),每一个滤波
器(filter),每一个神经元,只考虑感受野范围里面的信息。所以如果我们比较卷积神经网络
跟自注意力会发现,卷积神经网络可以看作是一种简化版的自注意力,因为在做卷积神经网
络的时候,只考虑感受野里面的信息。而在做自注意力的时候,会考虑整张图像的信息。在卷
积神经网络里面,我们要划定感受野。每一个神经元只考虑感受野里面的信息,而感受野的
大小是人决定的。而用自注意力去找出相关的像素,就好像是感受野是自动被学出来的,网
络自己决定感受野的形状。网络决定说以这个像素为中心,哪些像素是真正需要考虑的,哪
些像素是相关的,所以感受野的范围不再是人工划定,而是让机器自己学出来。关于自注意
力跟卷积神经网络的关系,读者可以读论文 “On the Relationship between Self-attention and
Convolutional Layers”,这篇论文里面会用数学的方式严谨地告诉我们,卷积神经网络就是自
注意力的特例。
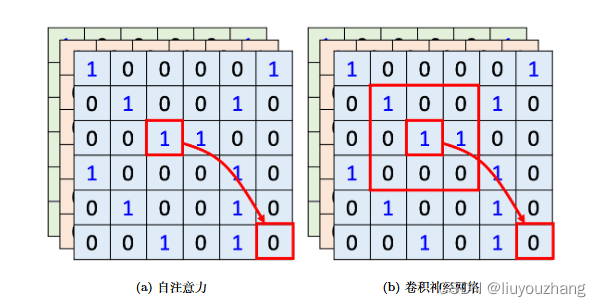
图 6.38 自注意力和卷积神经网络的区别
自注意力只要设定合适的参数,就可以做到跟卷积神经网络一模一样的事情。卷积神经网络的函数集(function set)与自注意力的函数集的关系如图 6.39 所示。所以自注意力是更
灵活的卷积神经网络,而卷积神经网络是受限制的自注意力。自注意力只要通过某些设计、某
些限制就会变成卷积神经网络。

图 6.39 卷积神经网络的函数集与自注意力的函数集的关系
既然卷积神经网络是自注意力的一个子集,说明自注意力更灵活。更灵活的模型需要更
多的数据。如果数据不够,就有可能过拟合。而比较有限制的模型,它适合在数据少的时候使
用,它可能比较不会过拟合。如果限制设的好,也会有不错的结果。谷歌的论文 “An Image
is Worth 16x16 Words: Transformers for Image Recognition at Scale” 把自注意力应用在图
像上面,把一张图像拆成 16 × 16 个图像块(patch),它把每一个图像块就想像成是一个字
(word)。因为一般自注意力比较常用在自然语言处理上面,所以我们可以想像每一个图像块
就是一个字。如图 6.40 所示,横轴是训练的图像的量,对谷歌来说用的所谓的数据量比较少,
也是我们没有办法用的数据量。这边有 1000 万张图,是数据量比较小的设置(setting),数
据量比较大的设置呢,有 3 亿张图像。在这个实验里面,自注意力是浅蓝色的这一条线,卷
积神经网络是深灰色的这条线。随着数据量越来越多,自注意力的结果越来越好。最终在数据
量最多的时候,自注意力可以超过卷积神经网络,但在数据量少的时候,卷积神经网络是可以
比自注意力得到更好的结果的。自注意力的弹性比较大,所以需要比较多的训练数据,训练
数据少的时候就会过拟合。而卷积神经网络的弹性比较小,在训练数据少的时候结果比较好。
但训练数据多的时候,它没有办法从更大量的训练数据得到好处。这就是自注意力跟卷积神
经网络的比较。
下一篇:自注意力与循环神经网络对比
来源:李宏毅深度学习教程笔记 LeeDL_Tutorial_v.1.1.1.pdf 132M Page131-133
https://github.com/datawhalechina/leedl-tutorial
相关文章:

机器学习,神经网络中,自注意力跟卷积神经网络之间有什么样的差异或者关联?
如图 6.38a 所示,如果用自注意力来处理一张图像,假设红色框内的“1”是要考虑的像素,它会产生查询,其他像素产生 图 6.37 使用自注意力处理图像 键。在做内积的时候,考虑的不是一个小的范围,而是整张图像的…...

这件事,准备考PMP的都必须知道
大家好,我是老原。 新的一月,新的困惑。最近接到的咨询很多,但的确出现了差异化的特质。 以前的粉丝朋友上来就问,我现在是项目经理,主要负责产品研发,我是考PMP还是NPDP好? 现在的粉丝朋友会…...
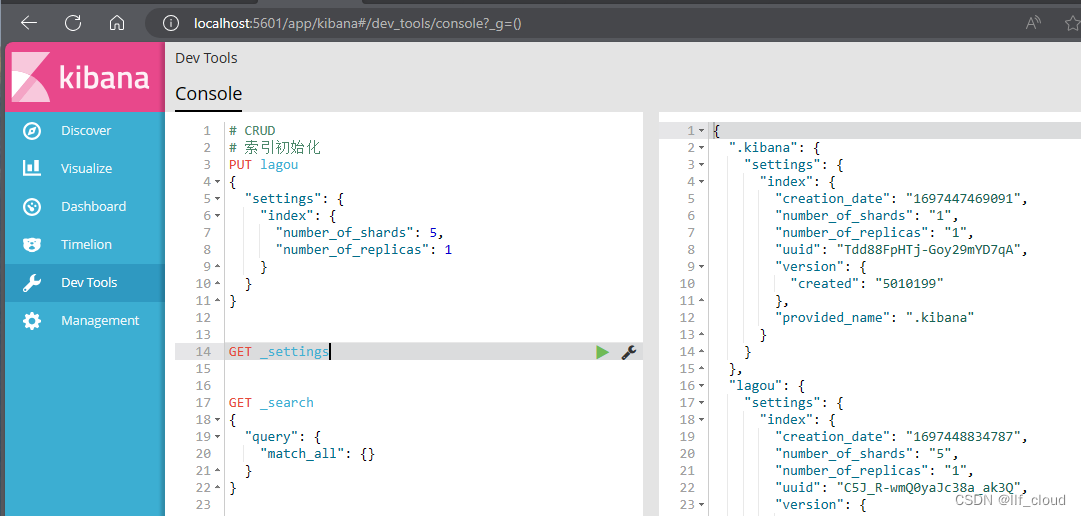
elasticsearch常用命令
Elasticsearch概念 ElasticsearchmysqlIndex(索引)数据库Type(类型)表Documents(文档)行Fields列 常用命令 索引 # 索引初始化,number_of_shards:分片数,不可修改;number_of_replicas:副本数,可修改 PUT lagou {"settings…...

2000-2021年上市公司MA并购溢价计算数据(含原始数据+Stata代码)
2000-2021年上市公司M&A并购溢价计算(原始数据Stata代码) 1、时间:2000-2021年 2、范围:沪深A股上市公司 3、指标: 原始数据指标:事件ID、公司ID、证券代码、业务编码、上市公司交易地位编码、首次公…...

移动端1px-从基本原理到开源解决方案介绍
1px 不够准确,应该说成 1 物理像素 为什么有 1px 这个问题?实现 1px 有哪些方法?这些方法分别有哪些优缺点?开源项目中使用的哪些解决方案?如何在项目中处理 1px 的相关问题? 基本概念 首先,我们…...

Linux——shell外壳程序
shell外壳程序 1. 什么是shell外壳程序 Linux严格意义上说的是一个操作系统,我们称之为“核心 “ ,但我们一般用户,不能直接使用核心。 而是通过核心的“外壳”程序,也就是所谓的shell。 shell是所有外壳程序的统称 平时程序员…...
攻防世界web篇-Training-WWW-Robots
直接点击给出的地址,然后会转到另一个网页界面,在这个界面,已经给出了提示,robots.txt 在浏览器中,直接在地址的后面加上robots.txt,会进到下面这个界面 因为对php语言一窍不通,所以这里纯粹就…...
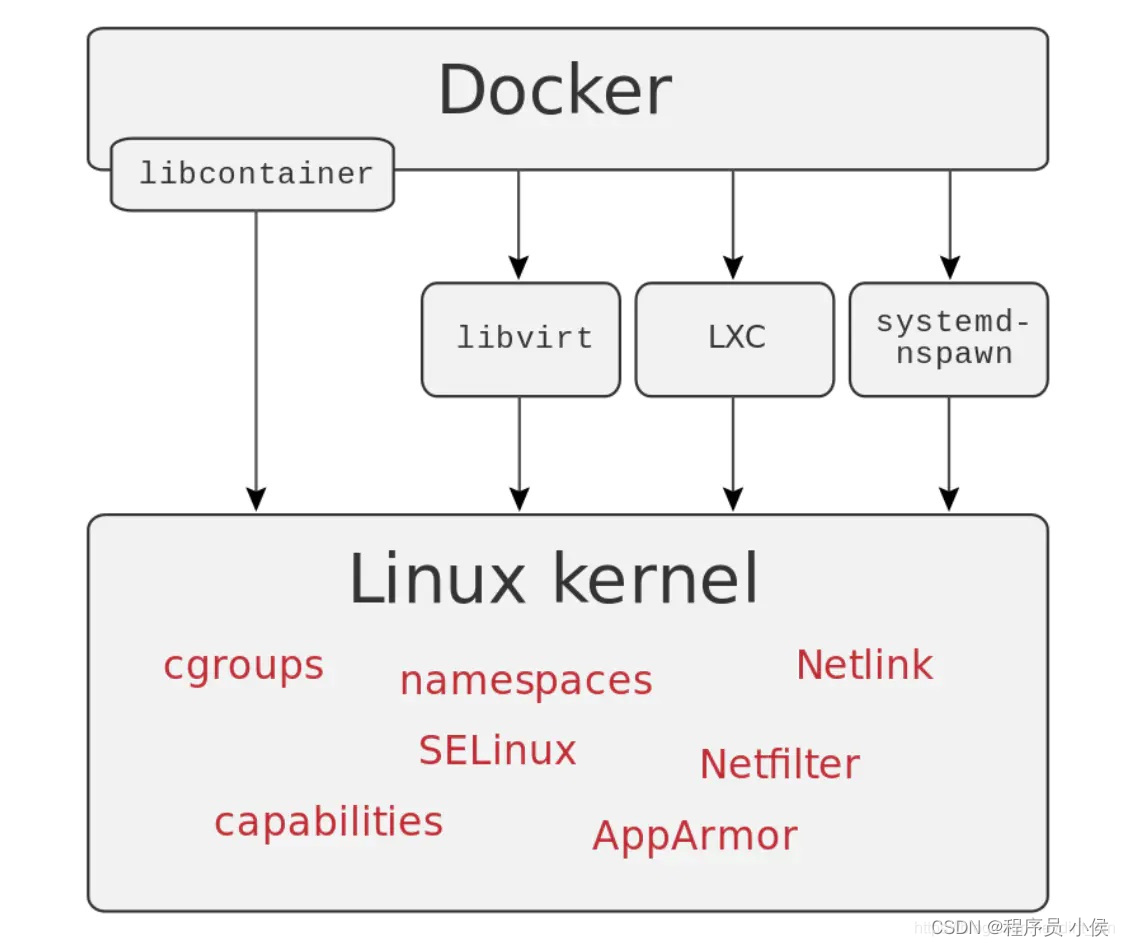
Docker是一个流行的容器化平台,用于构建、部署和运行应用程序。
文章目录 Web应用程序数据库服务器微服务应用开发环境持续集成和持续部署 (CI/CD)应用程序依赖项云原生应用程序研究和教育 🎈个人主页:程序员 小侯 🎐CSDN新晋作者 🎉欢迎 👍点赞✍评论⭐收藏 ✨收录专栏:…...
如何压缩ppt文件的大小?
如何压缩ppt文件的大小?要知道现在很多课件都是使用ppt文件,那么就导致ppt文件过大,我们很多时候电脑的存储空间就不够了。为了能够更好的存储这些ppt文件,我们通常会选择压缩ppt文件。怎么压缩ppt文件更快更好,没有损…...

8个视频剪辑素材网站,免费下载
找视频剪辑素材就上这8个网站,免费下载,可商用,赶紧收藏起来~ 免费视频素材 1、菜鸟图库 https://www.sucai999.com/video.html?vNTYxMjky 菜鸟图库网素材非常丰富,网站主要还是以设计类素材为主,高清视频素材也很多…...
-C++)
常用的二十种设计模式(上)-C++
C中常用的设计模式有很多,设计模式是解决常见问题的经过验证的最佳实践。以下是一些常用的设计模式: 单例模式(Singleton):确保一个类只有一个实例,并提供一个全局访问点。工厂模式(Factory&am…...

JS中var和let和const的区别
在我很早之前,我还在用着var,直到接触到了let与const,我才知道var造成的影响很多,我果断的抛弃了var,哈哈 让我为大家介绍一下它们的区别吧! 1.块级作用域 块作用域由 { }包括,let和const具有…...

如何利用IP定位技术进行反欺诈?
网络欺诈风险是指在互联网和数字领域中,存在各种类型的欺诈活动,旨在欺骗个人、组织或系统以获得非法获益。以下是一些常见的网络欺诈风险类型: 身份盗用:这是一种欺诈行为,涉及盗取他人的个人身份信息,如姓…...
wireshark抓包本地IDEA xml格式报文教程以及postman调用接口
1、选择 2、筛选...

MySQL学习(六)——视图和触发器
文章目录 1. 视图1.1 视图语法1.2 检查选项1.3 视图的更新1.4 视图的作用 2. 触发器2.1 介绍2.2 语法介绍2.3 触发器示例2.3.1 插入数据触发器2.3.2 修改数据触发器2.3.3 删除数据触发器 1. 视图 视图(View)是一种虚拟存在的表。视图中的数据并不在数据…...

那些你面试必须知道的ES6知识点
目录 1、var、let、const的区别2、作用域考题3、合并两个对象4、箭头函数和普通函数的区别5、Promise有几种状态6、find和filter的区别7、some和every的区别 1、var、let、const的区别 区别一: var有变量提升,而let和const没有 <script>console.l…...

AD9371 系列快速入口
参考资料: AD9371 JESD204 Interface Framework Generic JESD204B block designs AD9371 & AD9375 Prototyping Platform User Guide ADI™ Reference Designs HDL User Guide 相关设备 : ZCU106ADRV9371CPRO33-30.726 dB 衰减 AD9371ZCU102 移植到…...

Jenkins+vue发布项目
在Jenkins 中先创建一个任务名称 然后进行下一步,放一个项目 填写一些参数 参数1: 参数2: 参数3:参数4: 点击保存就行了 配置脚本 // git def git_url http://gitlab.xxxx.git def git_auth_id GITEE_RIVER…...

RSTP详解:对比STP,到底改进了什么?
一、RSTP概述 IEEE 802.1W中定义的RSTP可以视为STP的改进版本,RSTP在许多方面对STP进行了优化,它的收敛速度更快,而且能够兼容STP。 二、RSTP对STP的改进 改进点1:端口角色 、 改进点2:端口状态 RSTP的状态规范缩…...
从0到1,申请cos服务器并上传图片到cos文件服务器
目录 准备工作 Java代码编写 控制台打印 整理成工具类 编写接口 Postman测试 准备工作 1.进入网址腾讯云 产业智变云启未来 - 腾讯 (tencent.com) 2.搜索cos,点击立即使用,刚开始会免费赠送你 3.存储都是基于桶的,先创建桶,在桶里面创…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
