面试知识点--基础篇
文章目录
- 前言
- 一、排序
- 1. 冒泡排序
- 2. 选择排序
- 3. 插入排序
- 4. 快速单边循环排序
- 5. 快速双边循环排序
- 6. 二分查找
- 二、集合
- 1.List
- 2.Map
前言
提示:以下是本篇文章正文内容,下面案例可供参考
一、排序
1. 冒泡排序
冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。所以,如果两个元素相等,是不会再交换的;如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。
时间复杂度:O(n²)
public class BubbleSort {/*** 冒泡排序* 1. 比较相邻的元素。如果第一个比第二个大,就交换他们两个。* 2. 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。* 3. 针对所有的元素重复以上的步骤,除了最后一个。* 4. 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较*/@Testpublic void bubbleSortDemo() {Integer[] array = {1, 12, 6, 19, 18, 9, 66, 89};for (int i = 0; i < array.length - 1; i++) {boolean mark = false; //标记是否有交换数据,如果没有交换数据则表明数组已是有序数组,无需再进行排序for (int j = 0; j < array.length - 1 - i; j++) {if (array[j] > array[j + 1]) {int temp = array[j];array[j] = array[j+1];array[j+1] = temp;mark = true ;}}if(!mark){//没有交换数据则表明数组已是有序数组,无需再进行排序break;}System.out.println(Arrays.toString(array));}
// System.out.println(Arrays.toString(array));}/*** 冒泡排序加强版* 记录最后一次交换索引的位置**/@Testpublic void bubbleSortPlusDemo() {Integer[] array = {1, 12, 6, 19, 18, 9, 66, 89};int lastIndex = array.length - 1;while (true) {int index = 0;for (int j = 0; j <lastIndex; j++) {System.out.println("array : "+Arrays.toString(array)+" ::: "+j);if (array[j] > array[j + 1]) {int temp = array[j];array[j] = array[j+1];array[j+1] = temp;//记录最后一次交换索引的位置index = j;}}//记录最后一次交换索引的位置lastIndex = index;if(lastIndex==0){break;}System.out.println(Arrays.toString(array));}
// System.out.println(Arrays.toString(array));}
}
2. 选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法
最好复杂度:O(n^2)
最差复杂度:O(n^2)
public class SelectionSort {/*** 选择排序 是一种简单直观的排序算法。* 1. 第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,* 2. 再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。* 3. 以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法*/@Testpublic void selectionSortDemo() {Integer[] array = {1, 12, 6, 19, 18, 9, 66, 89};for (int i = 0; i < array.length; i++) {int tempIndex = i;//用于记录最小索引for (int j = i; j < array.length; j++) {//判断最小值if(array[tempIndex] > array[j]){tempIndex = j; // 获取最小索引}}//与最小索引进行替换int temp = array[i];array[i] = array[tempIndex];array[tempIndex] = temp;}System.out.println(Arrays.toString(array));}
}3. 插入排序
插入排序,一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法 。
插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动
空间复杂度:O(1)
时间复杂度:O(N^(1-2))
public class InsertionSort {/*** 插入排序* 将数组分为两个区域,排序区和未排序区,每一轮从未排序区选取第一个元素与排序区做对比,直到对比结束。默认第一个是排序好的* 例:[6, 5, 2]* 1. 默认6是排序好的,5是未排序的 ---> 6>5 交换位置 -->[5, 6, 2]* 2. 5,6是排序好的,2是未排序的 ---> 2<6 6往后移一位,然后2还要与5比较 2<5 --》[2, 5, 6] 直到2找到合适位置*/@Testpublic void insertionSortDemo() {Integer[] array = {1, 12, 6, 19, 18, 9, 66, 89};for (int i = 1; i < array.length; i++) {//默认第一个是排序好的,所以要从索引为1的位置开始int insertVal = array[i]; // 待插入的值int index = i - 1; //待比较的索引while (index >= 0) {if (insertVal < array[index]) {//如果待插入的值比前面的值小array[index + 1] = array[index]; //那么比较的值往后移一位index--;}else{break;}}//插入值array[index + 1] = insertVal;System.out.println(Arrays.toString(array));}
// System.out.println(Arrays.toString(array));}@Testpublic void insertionSortDemo02() {Integer[] array = {1, 12, 6, 19, 18, 9, 66, 89};for (int i = 1; i < array.length; i++) {for (int j = i - 1; j >= 0; j--) {if (array[j + 1] < array[j]) {int temp = array[j + 1];array[j + 1] = array[j];array[j] = temp;} else {break;}}System.out.println(Arrays.toString(array));}
// System.out.println(Arrays.toString(array));}
}4. 快速单边循环排序
快速排序采用的是分治思想,即在一个无序的序列中选取一个任意的基准元素pivot,利用pivot将待排序的序列分成两部分,前面部分元素均小于或等于基准元素,后面部分均大于或等于基准元素,然后采用递归的方法分别对前后两部分重复上述操作,直到将无序序列排列成有序序列
public class QuickSort {@Testpublic void quickSortDemo() {Integer[] array = {1, 12, 6, 19, 18, 9, 66, 89};recursionQuickSort(array, 0, array.length - 1);System.out.println(Arrays.toString(array));}/*** 递归调用** @param array* @param startIndex* @param endIndex*/public void recursionQuickSort(Integer[] array, Integer startIndex, Integer endIndex) {if (startIndex >= endIndex) {//如果起始边界大于等于结束边界 结束递归return;}//获取基准点的索引位置,此时比基准点小的全在左侧,比基准点大的全在右侧,可以分而治之Integer pvIndex = quickSort(array, startIndex, endIndex);//分而治之-->对基准点左侧元素递归调用recursionQuickSort(array, startIndex, pvIndex - 1);//分而治之-->对基准点右侧元素递归调用recursionQuickSort(array, pvIndex + 1, endIndex);}/*** 单边循环快速排序---->基准点选择最右侧得元素* 1. 选择右侧元素做为基准点* 2. I 指针维护小于基准点的边界,也就是每次交换的目标索引* 3. J 指针负责找到比基准点小的元素,一旦找到则与 I 索引交换* 4. 最后交换基准点与 I 交换, 因为基准点选择是的右侧的, I 一定是大于基准点的,所以大于基准点的放在右** @param array*/public int quickSort(Integer[] array, Integer startIndex, Integer endIndex) {int pv = array[endIndex];//设置基准点 基准点选择最右侧得元素int j = startIndex; //设置比基准点小的元素索引for (int i = startIndex; i < endIndex; i++) {if (array[i] < pv) { //如果当前元素比基准点小 那么将当前元素与基准点大的元素进行交换int temp = array[i];array[i] = array[j];array[j] = temp;j++; //默认比基准点小的元素索引为0,一旦发现比基准点小的元素就与J交换位置,此时就能保证比基准点小的元素全在基准点的左侧}}//调换基准点元素,因为基准点选择的是最右侧得元素,所以与 j(此时的j是++后的) 互换位置,换过去的一定是大于基准点的元素array[endIndex] = array[j];array[j] = pv;
// System.out.println(Arrays.toString(array));return j;}
}
5. 快速双边循环排序
快速排序采用的是分治思想,即在一个无序的序列中选取一个任意的基准元素pivot,利用pivot将待排序的序列分成两部分,前面部分元素均小于或等于基准元素,后面部分均大于或等于基准元素,然后采用递归的方法分别对前后两部分重复上述操作,直到将无序序列排列成有序序列
public class QuickSort {@Testpublic void quickSortDemo() {Integer[] array = {1, 12, 6, 19, 18, 9, 66, 89};recursionQuickSort(array, 0, array.length - 1);System.out.println(Arrays.toString(array));}/*** 递归调用** @param array* @param startIndex* @param endIndex*/public void recursionQuickSort(Integer[] array, Integer startIndex, Integer endIndex) {if (startIndex >= endIndex) {//如果起始边界大于等于结束边界 结束递归return;}//获取基准点的索引位置,此时比基准点小的全在左侧,比基准点大的全在右侧,可以分而治之Integer pvIndex = quickSort(array, startIndex, endIndex);//分而治之-->对基准点左侧元素递归调用recursionQuickSort(array, startIndex, pvIndex - 1);//分而治之-->对基准点右侧元素递归调用recursionQuickSort(array, pvIndex + 1, endIndex);}/*** 双边循环快速排序---->基准点选择最左侧的元素* 1. 选择左侧元素做为基准点* 2. rl指针负责从右向左找比基准点小的元素,lr指针负责从左向右找比基准点大的元素。* 3. 一旦找到,二者交换 直到 rl == lr 说明两个指针重合,结束循环* 4. 最后交换基准点位置** @param array*/public int quickSort(Integer[] array, Integer startIndex, Integer endIndex) {Integer pv = array[startIndex]; //确定基准点--以最左侧为基准点Integer lrIndex = startIndex;//确定比基准点大的索引--》左-右Integer rlIndex = endIndex;//确定比基准点小的索引--》右-左while (rlIndex > lrIndex) {//从右向左找比基准点小的索引while (rlIndex > lrIndex && pv <= array[rlIndex]) {rlIndex--;}//从左向右找比基准点大的索引while (rlIndex > lrIndex && pv >= array[lrIndex]) {lrIndex++;}//互换位置int temp = array[lrIndex];array[lrIndex] = array[rlIndex];array[rlIndex] = temp;}//基准点换位置array[startIndex] = array[rlIndex];array[rlIndex] = pv;return rlIndex;}
}6. 二分查找
折半查找法也称为二分查找法,它充分利用了元素间的次序关系,采用分治策略,可在最坏的情况下用O(log n)完成搜索任务。它的基本思想是:(这里假设数组元素呈升序排列)将n个元素分成个数大致相同的两半,取a[n/2]与欲查找的x作比较,如果x=a[n/2]则找到x,算法终止;如 果x<a[n/2],则我们只要在数组a的左半部继续搜索x;如果x>a[n/2],则我们只要在数组a的右 半部继续搜索x。
public class BinarySearch {@Testpublic void binarySearchDemo() {//二分查找默认有序数组Integer[] array = {1, 6, 9, 12, 18, 19, 66, 89};//调用二分查找方法int index = binarySearch(array, 0, array.length, 12);System.out.println(index);}/*** 二分查找* 折半查找法也称为二分查找法,它充分利用了元素间的次序关系,采用分治策略,可在最坏的情况下用O(log n)完成搜索任务。* 它的基本思想是:(这里假设数组元素呈升序排列)将n个元素分成个数大致相同的两半,取a[n/2]与欲查找的x作比较,如果x=a[n/2]则找到x,* 算法终止;如 果x<a[n/2],则我们只要在数组a的左半部继续搜索x;如果x>a[n/2],则我们只要在数组a的右 半部继续搜索x。** @param array* @param leftRange 左边界* @param rightRange 右边界* @param target 目标元素* @return*/public int binarySearch(Integer[] array, Integer leftRange, Integer rightRange, Integer target) {while (rightRange >= leftRange) {//获取中间索引位置 防止整数溢出int middleIndex = (leftRange + rightRange) >>> 1; // 第一种解决办法//推导:middleIndex = (leftRange + rightRange)/2 ==>leftRange - leftRange/2 + rightRange/2 ==>leftRange + (rightRange - leftRange) / 2;
// int middleIndex = leftRange + (rightRange - leftRange) / 2; // 第二解决办法if (array[middleIndex] == target) {//中间值与目标值正好相等return middleIndex;} else if (array[middleIndex] < target) {//中间值小于目标值leftRange = middleIndex + 1; // 设置左边界} else if (array[middleIndex] > target) {//中间值大于目标值rightRange = middleIndex - 1;// 设置右边界}}return -1;}
}二、集合
1.List
深入了解Collection的实现类
1. ArrayList扩容机制
- ArrayList是懒惰扩容机制,即没有添加元素前即使指定了容量,也不会真正创建数组
- add(E e)首次扩容为10,非首次扩容为上次数组长度的1.5倍
- addAll(Collection<? extends E> c) 首次扩容会将默认长度10与集合长度做对比那个大用哪个,非首次扩容会对比原容量的1.5倍与集合长度做对比,那个大用哪个。
2. ArrayList遍历时可以修改集合吗?
ArrayList是 fail-fast 的典型代表,遍历时不可以修改集合。在遍历时会拿到集合的长度,如果集合增加或减少那么长度就会改变,遍历时发现长度变化,则会直接报错。
CopyOnWriteArrayList是 fail-safe 的典型代表,遍历时可以修改集合。在遍历时会复制集合,当集合被修改时会创建新的集合,不会影响遍历的集合
3. ArrayList 和 LinkedList的区别?
- ArrayList的底层是数组,内存是连续的,可以利用cpu缓存。 LinkedList的底层是双向链表,内存无需连续。
- ArrayList基于索引的随机访问效率高,基于内容的随机访问效率和 LinkedList一样,都需要从头开始遍历。
- ArrayList的尾部插入,删除速度快,无需移动数组,越靠近头部的插入,删除越慢,因为需要移动数组。
- LinkedList头尾插入,删除性能高。中间插入删除效率低,主要因为从头遍历比较耗时。
2.Map
1. Map 1,7 和 1.8有何不同?
1.7:底层使用数组+链表
1.8:底层使用数组+链表或红黑树
2. 为何使用红黑树?为何不直接用红黑树?
- 防止链表长度超长时影响性能,所以使用红黑树。
- 树化是一种偶然情况,是用来防止攻击的。正常情况下在负载因子为0.75.链表长度为8出现的概率是极低的。
- 链表长度设置为8,就是为了降低树化的机率。
- 链表的查询效率为O(1),红黑树的查询效率为O(log2 N),而且红黑树的TreeNode比链表Node更占空间。
3. 链表何时会树化,红黑树何时会退化成链表?
- 链表长度超过阈值(8)且数组长度大于64,满足以上链表会进化成红黑树。
- 数组扩容时拆分红黑树的元素个数小于等于6,则会退化成链表。
- 删除树节点时,若root 、root.left、root.right、root.let.let有一个为null也会退化成链表。
4. 多线程下对Map进行put造成数据错乱?

5. Map1.7 扩容为什么会造成死链
因为JDK1.7 Map使用头插法,在多线程下扩容时容易造成死链。例:链表中有a,b两个元素,其中a的下一个元素是b,当线程T1,T2同时对数组进行扩容时,假设T2先执行,因为头插法扩容后的顺序为b,a,此时b的下一个元素时a。由于扩容不会对元素进行更改,此时b指向a,同时a又指向b,当T1线程对数组进行扩容时就会造成死链。



6. Map的key是否可以为null,对象作为key应如何处理?
- HashMap的key可以为null,其余Map的实现则不可以(tableMap)。
- 对象作为key应重写hashCode方法和equals方法,且key的内容不可以被修改。
相关文章:

面试知识点--基础篇
文章目录 前言一、排序1. 冒泡排序2. 选择排序3. 插入排序4. 快速单边循环排序5. 快速双边循环排序6. 二分查找 二、集合1.List2.Map 前言 提示:以下是本篇文章正文内容,下面案例可供参考 一、排序 1. 冒泡排序 冒泡排序就是把小的元素往前调或者把大…...
FIFO设计16*8,verilog,源码和视频
名称:FIFO设计16*8,数据显示在数码管 软件:Quartus 语言:Verilog 代码功能: 使用verilog语言设计一个16*8的FIFO,深度16,宽度为8。可对FIFO进行写和读,并将FIFO读出的数据显示到…...

#力扣:2769. 找出最大的可达成数字@FDDLC
2769. 找出最大的可达成数字 - 力扣(LeetCode) 一、Java class Solution {public int theMaximumAchievableX(int num, int t) {return num 2*t;} }...

Juniper防火墙SSG-140 session 过高问题
1.SSG-140性能参数 2.问题截图 3.解决方法 (1)通过telnet 或 consol的方法登录到防火墙; (2)使用get session 查看总的session会话数,如果大于300 一般属于不正常情况 (3)使用get…...

Spring Boot 3.2四个新特点提升运行性能
随着 Spring Framework 6.1 和 Spring Boot 3.2 普遍可用性的临近,我们想分享一下 Spring 团队为让开发人员优化其应用程序的运行时效率而做出的几项努力的概述。 我们将介绍以下技术和用例: Spring MVC 将使用 基于JDK 21 虚拟线程 Web 堆栈使用 Spri…...

一阶系统阶跃响应实现规划方波目标值
一阶系统单位阶跃响应 一阶系统传递函数,实质是一阶惯性环节,T为一阶系统时间常数。 输入信号为单位阶跃函数,数学表达式 单位阶跃函数拉氏变换 输出一阶系统单位阶跃响应 拉普拉斯反变换 使用前向差分法对一阶系统离散化 将z变换写成差分方…...

项目经理如何去拆分复杂项目?
代码的横向分层,维度是根据复杂度来的,可保证代码便于开发和维护 1、因为强类型的原因,把变动大的分到数据库来解决,这是一种后端分离。 2、因为发布难的原因,所以用稳定的引擎来解决问题,然后用数据库配置…...
python二次开发Solidworks:修改实体尺寸
立方体原始尺寸:100mm100mm100mm 修改后尺寸:10mm100mm100mm import win32com.client as win32 import pythoncomdef bin_width(width):myDimension Part.Parameter("D1草图1")myDimension.SystemValue width def bin_length(length):myDime…...
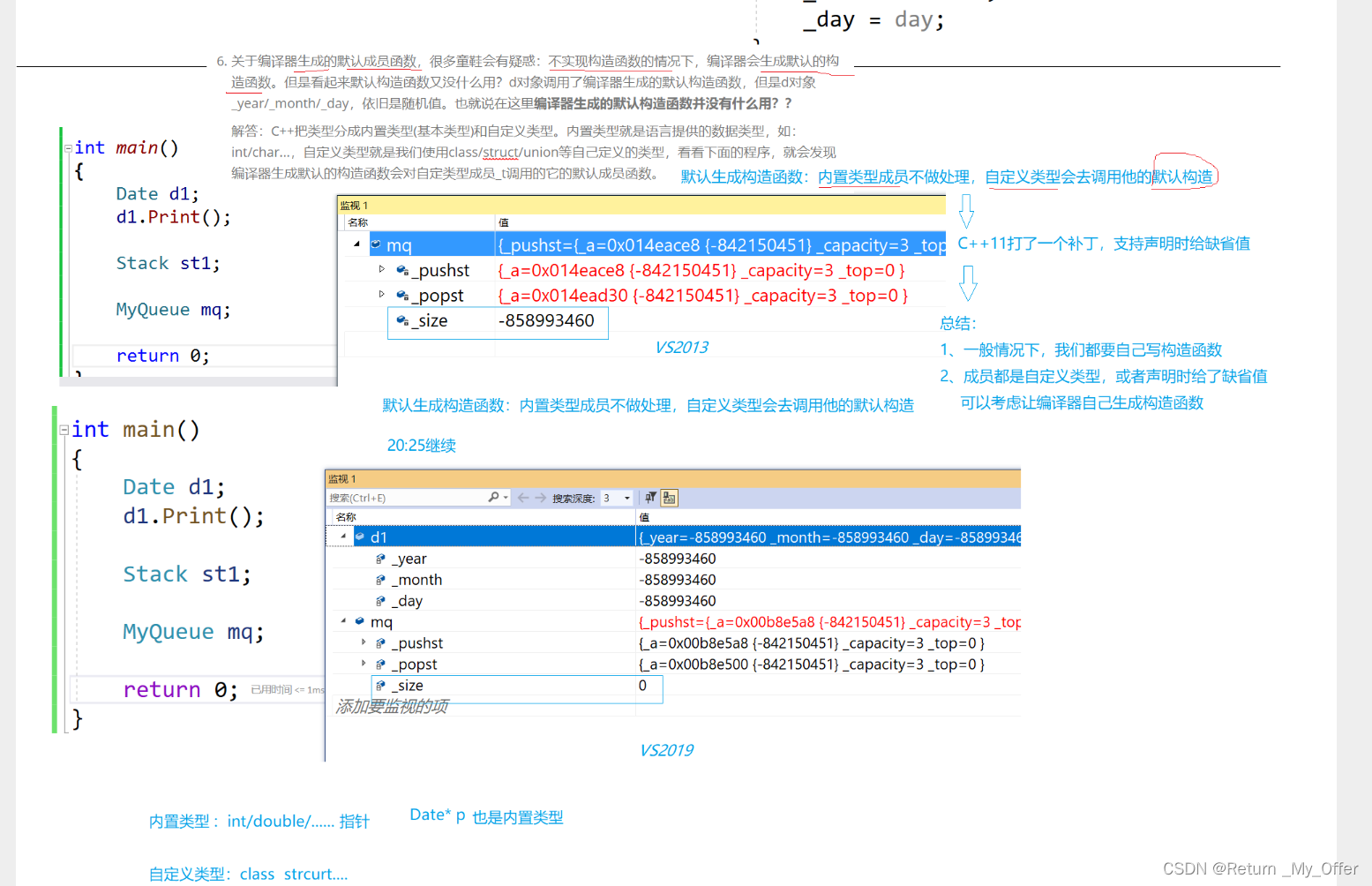
【C++】:类和对象(中)之类的默认成员函数——构造函数and析构函数
1.类的6个默认成员函数 如果一个类中什么成员都没有,简称为空类 空类中真的什么都没有吗?并不是,任何类在什么都不写时,编译器会自动生成以下6个默认成员函数 默认成员函数:用户没有显式实现,编译器会生成…...
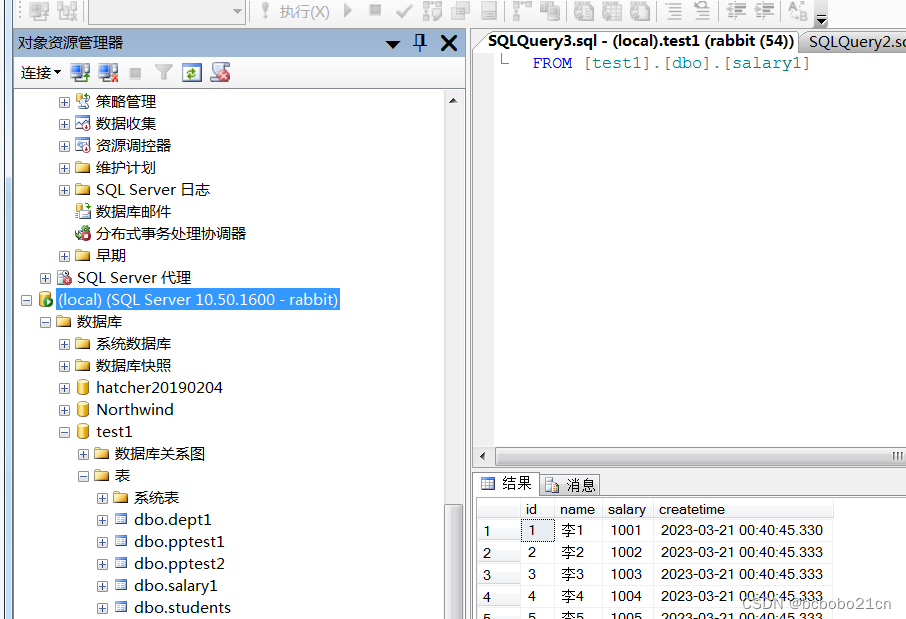
sqlserver系统存储过程添加用户学习
sqlserver有一个系统存储过程sp_adduser;从名字看是添加用户的;操作一下, 从错误提示看还需要先添加一个登录名,再执行一个系统过程sp_addlogin看一下, 执行完之后看一下,安全性-登录名下面有了rabbit&…...

Monocle 3 | 太牛了!单细胞必学R包!~(一)(预处理与降维聚类)
1写在前面 忙碌的一周结束了,终于迎来周末了。🫠 这周的手术真的是做到崩溃,2天的手术都过点了。🫠 真的希望有时间静下来思考一下。🫠 最近的教程可能会陆续写一下Monocle 3,炙手可热啊,欢迎大…...

基于VCO的OTA稳定性分析的零交叉时差模型研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
大数据Hadoop之——部署hadoop+hive+Mysql环境(window11)
一、安装JDK8 【温馨提示】对应后面安装的hadoop和hive版本,这里使用jdk8,这里不要用其他jdk了,可能会出现一些其他问题。 1)JDK下载地址 Java Downloads | Oracle 按正常下载是需要先登录的,这里提供一个不用登录下载…...

app爬虫中的Airtest元素存在或等待
app爬虫中的Airtest元素存在或等待 一. poco等待 等待无错误 等待元素10秒。如果它没有出现,则不会引发任何错误。 poco(xxx).wait(timeout10)您还可以在.wait()之后执行一些操作,如click或long_click poco(xxx).wait(timeout10).click() poco(xxx).…...

Flink学习之旅:(三)Flink源算子(数据源)
1.Flink数据源 Flink可以从各种数据源获取数据,然后构建DataStream 进行处理转换。source就是整个数据处理程序的输入端。 数据集合数据文件Socket数据kafka数据自定义Source 2.案例 2.1.从集合中获取数据 创建 FlinkSource_List 类,再创建个 Student 类…...

SQL INSERT INTO 语句(在表中插入)
SQL INSERT INTO 语句 INSERT INTO 语句用于向表中插入新的数据行。 SQL INSERT INTO 语法 INSERT INTO 语句可以用两种形式编写。 第一个表单没有指定要插入数据的列的名称,只提供要插入的值,即可添加一行新的数据: INSERT INTO table_n…...
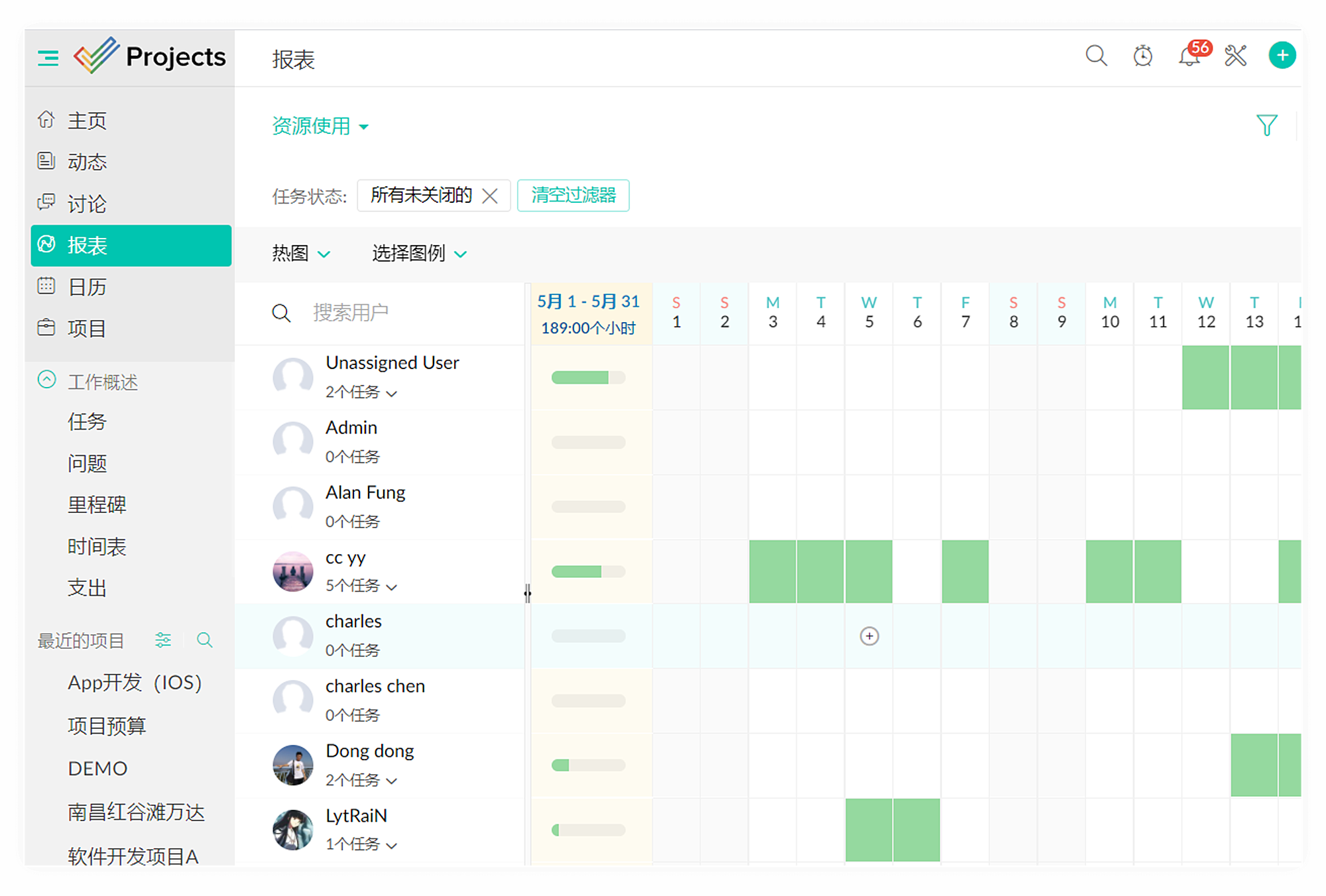
2023年最佳项目管理软件排行榜揭晓!
根据网络数据调查结果显示,今年有77%的组织将效率列为优先事项,而82%的领导人确认投资于新的项目管理和工作管理方案以提高效能。然而随着对价值的重新关注,选择适合的工程项目管理软件变得比以往任何时候都更加重要。好消息是通过对39个主要…...
【java】A卷+B卷)
华为OD DNA序列(100分)【java】A卷+B卷
华为OD统一考试A卷B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应20022部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入ÿ…...
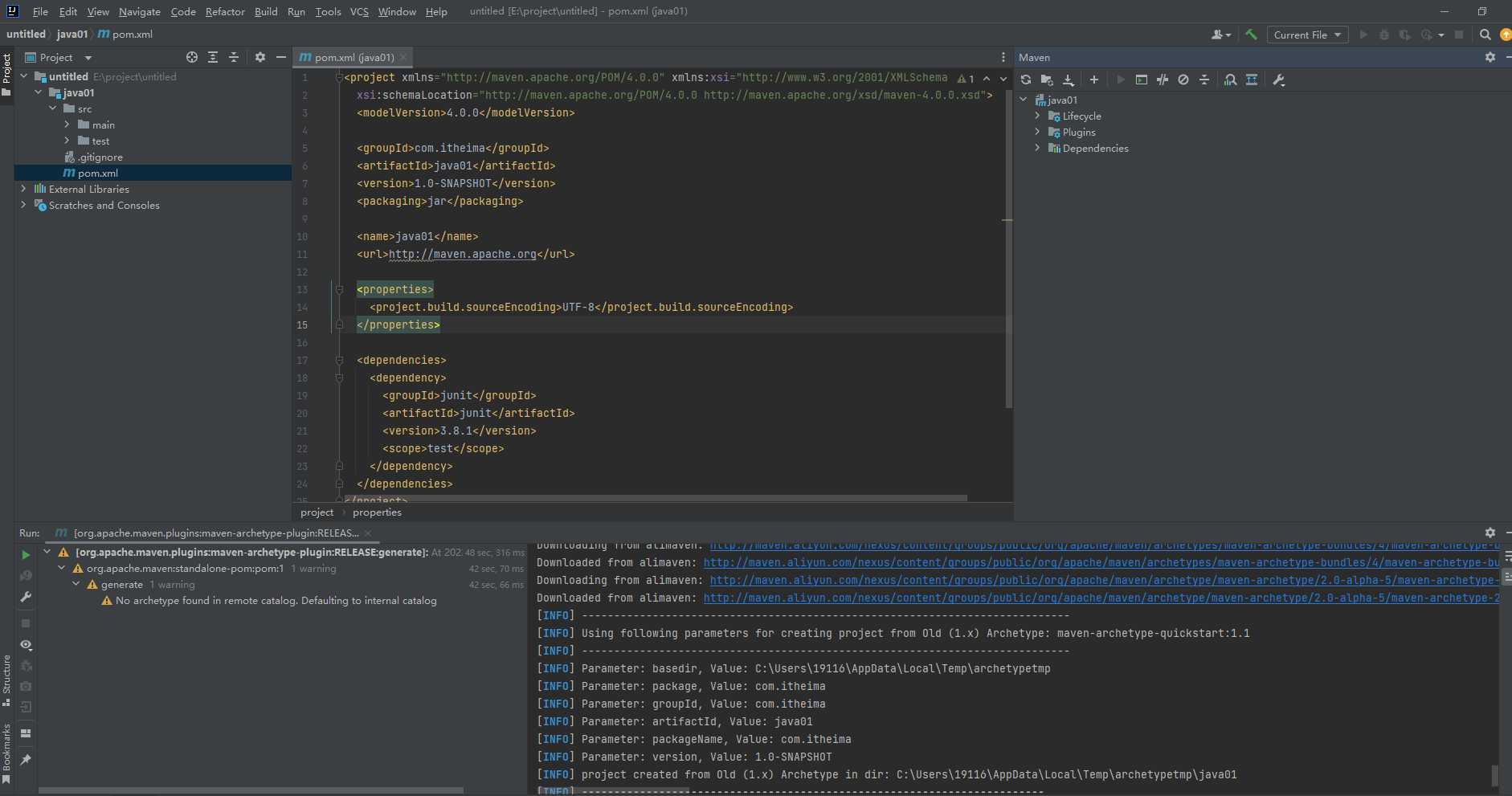
idea2023配置maven
看过【黑马程序员Maven全套教程,maven项目管理从基础到高级,Java项目开发必会管理工具maven】https://www.bilibili.com/video/BV1Ah411S7ZE?p9&vd_sourceedf9d91e5a0a27db51e3d6d4b9400637 配置的,前提要素配置也在这个课程里有啦&…...
Python 文件打包成可执行文件
打包 要将Python脚本打包成可执行文件,常见的做法是使用PyInstaller或cx_Freeze工具。下面是使用PyInstaller的基本步骤: 使用conda安装pyinstaller (建议) conda install -c conda-forge pyinstaller上面的命令从conda-forge通…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
