Peter算法小课堂—正整数拆分
大家可能会想:正整数拆分谁不会啊,2年级就会了,为啥要学啊
例题
正整数拆分有好几种,这里我们列举两种讲。
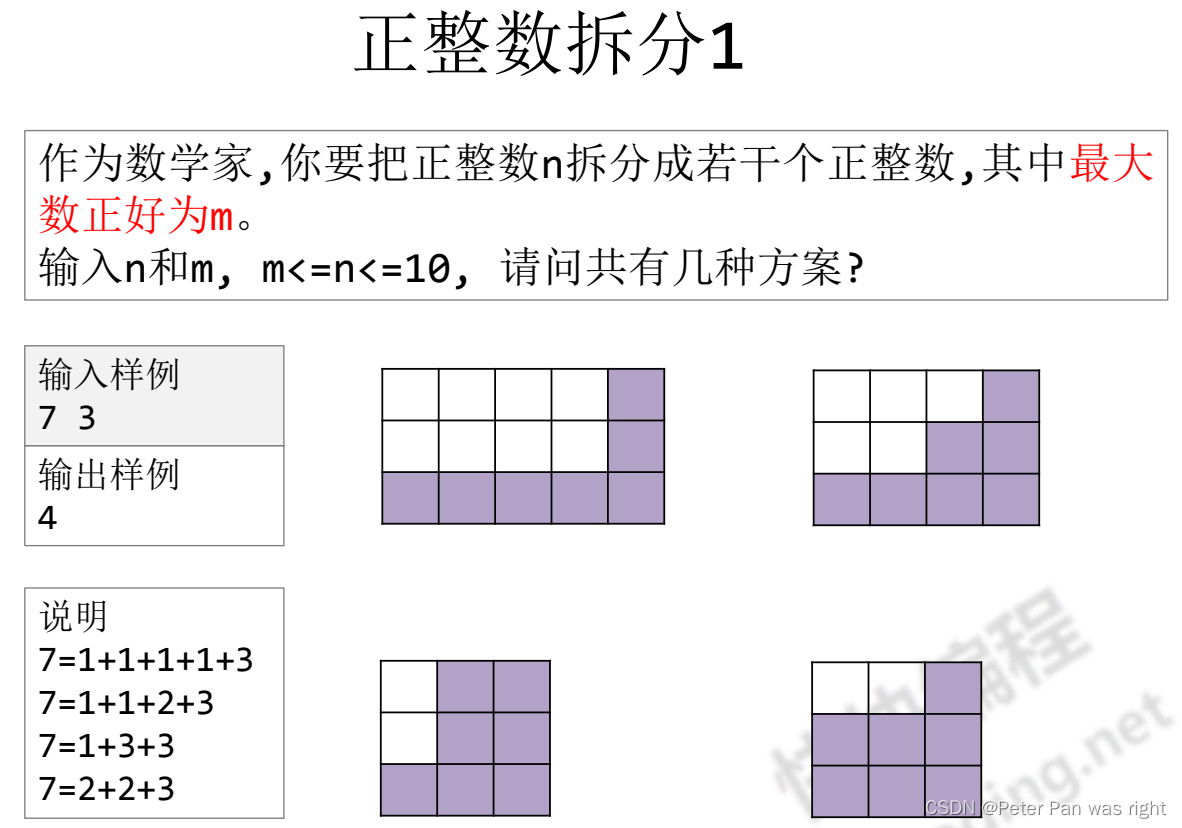
关系
我们看着第一幅图,头向左转90°,记住你看到的图,再来看第二幅图,你会惊奇的发现:第一幅图向左转90°就变成了第二幅图!因此,我们做出来一道题,就能推出另外一题。这种情况我们称之为Ferrers图
例2
我们先思考状态定义:f[i][j]表示把i恰好分成j个正整数的方案数
后面考虑状态转移方程,第一步先列表格。

我相信聪明的你们已经发现了规律:f[9][4]=1+2+2+1(i=5那行)f[8][3]=1+2+1(i=5那行的前4个)
后面,我们用数学方法推导一下规律:

因此得到状态转移方程:f[i][j]=f[i-j][1]+f[i-j][2]+……+f[i-j][j],但是时间复杂度为O(n^3)。于是我们进行优化。
我们看到f[i-j][1]+f[i-j][2]+……+f[i-j][j-1]=f[i-1][j-1],为什么因为根据前面的状态转移方程,f[i-1][j-1]等于f[i-j][1]+f[i-j][2]+……+f[i-j][j-1]。最后,我们的状态转移方程变为f[i][j]=f[i-1][j-1]+f[i-j][j]!
最后给个代码,
cin>>n>>m;
for(int i=1;i<=n;i++) f[i][1]=1;
for(int j=2;j<=m;j++)for(int i=j;i<=n;i++)f[i][j]=f[i-1][j-1]+f[i-j][j];
cout<<f[n][n]<<endl;变种
 太戈编程习题
太戈编程习题
456. 数的划分
题目描述
将整数n分成k份,且每份不能为空。任意两个方案不能相同(不考虑顺序)。 例如:n=7,k=3,下面三种分法被认为是相同的。 1,1,5;1,5,1;5,1,1; 问有多少种不同的分法。
#include <bits/stdc++.h>
using namespace std;
#define N 210
#define K 16
int n,k,f[N][K];
int main(){freopen("partition.in","r",stdin);freopen("partition.out","w",stdout);cin>>n>>k;for(int i=1;i<=n;i++) f[i][1]=1;for(int j=2;j<=k;j++)for(int i=j;i<=n;i++)f[i][j]=f[i-1][j-1]+f[i-j][j];cout<<f[n][k]<<endl;return 0;
}457. 训练计划
题目描述
要想成为编程高手,必须独立编程n个小时。作为编程教练,你希望为孩子们设计一套训练计划,将n个小时拆分成若干天完成。已知每天最多安排不能超过k小时,你的训练计划要求每天的训练量不能出现下降。请问一共有多少种训练方案?
#include <bits/stdc++.h>
using namespace std;
#define N 350
#define K 34
long long n,k,f[N][K];
int main(){freopen("training.in","r",stdin);freopen("training.out","w",stdout);cin>>n>>k;for(long long i=1;i<=n;i++) f[i][1]=1;for(long long j=2;j<=k;j++)for(long long i=j;i<=n;i++)f[i][j]=f[i-1][j-1]+f[i-j][j];long long ans=0;for(long long i=1;i<=k;i++)ans+=f[n][i];cout<<ans<<endl;return 0;
}希望大家可以点个赞、关个住,谢谢o(*^@^*)o
相关文章:

Peter算法小课堂—正整数拆分
大家可能会想:正整数拆分谁不会啊,2年级就会了,为啥要学啊 例题 正整数拆分有好几种,这里我们列举两种讲。 关系 我们看着第一幅图,头向左转90,记住你看到的图,再来看第二幅图,你…...

EDUSRC--简单打穿某985之旅
免责声明: 文章中涉及的漏洞均已修复,敏感信息均已做打码处理,文章仅做经验分享用途,切勿当真,未授权的攻击属于非法行为!文章中敏感信息均已做多层打马处理。传播、利用本文章所提供的信息而造成的任何直…...

vue2升级到vue2.7
vue2升级到vue2.7 小小的改进,大大的提升 只需要简单修改,开发体验得到大大提升. 为什么要升级Vue2.7 不能拒绝的理由: 组合式 API(解决mixins问题:命名冲突,隐式依赖)单文件组件内的 <script setup>语法模板表达式中支持 ESNext 语法(可选链:?.、空值合并:??)单文…...

【django2.0之Rest_Framework框架一】rest_framework序列器介绍
Django RestFramework(简称DRF) 提供了序列化器Serialzier的定义,可以帮助我们简化序列化与反序列化的过程,不仅如此,还提供丰富的类视图、扩展类、视图集来简化视图的编写工作。REST framework还提供了认证、权限、限流、过滤、分页、接口文…...
Mock 测试详解:什么是 Mock 测试
Mock测试 什么是 Mock ? Mock 的意思就是,当你很难拿到源数据时,你可以使用某些手段,去获取到跟源数据相似的假数据,拿着这些假数据,前端可以先行开发,而不需要等待后端给了数据后再开发。 Mo…...

Android端自定义铃声
随着移动应用竞争进入红海时代,如何在APP推送中别出心裁显得尤为重要。例如对自己的APP推送赋予独特的推送铃声,能够给用户更加理想的使用体验。 1、个性化提醒铃声有助于当收到特定类型的消息时,用户能够立刻识别出来。 2、不同的推送铃声…...

docker mysql 5.7
1.docker 安装mysql 5.7 docker pull mysql:5.72.配置容器MySQL数据、配置、日志挂载宿主机目录 # 宿主机创建数据存放目录映射到容器 mkdir -p /usr/local/docker_data/mysql/data# 宿主机创建配置文件目录映射到容器 mkdir -p /usr/local/docker_data/mysql/conf #(需要在…...

MySQL中如何进行分库分表的设计和实现?
分库分表是一种常用的数据库扩展方式,可以提高数据库的并发处理能力和扩展性,下面是分库分表的设计和实现的一般步骤: 数据库选择:选择合适的数据库管理系统(DBMS),如MySQL,支持分库…...

linux 安装谷歌浏览器和对应的驱动
创建文件install-google-chrome.sh #! /bin/bash# Copyright 2017-present: Intoli, LLC # Source: https://intoli.com/blog/installing-google-chrome-on-centos/ # # Redistribution and use in source and binary forms, with or without # modification, are permitted p…...

FPGA的通用FIFO设计verilog,1024*8bit仿真,源码和视频
名称:FIFO存储器设计1024*8bit 软件:Quartus 语言:Verilog 本代码为FIFO通用代码,其他深度和位宽可简单修改以下参数得到 reg [7:0] ram [1023:0];//RAM。深度1024,宽度8 代码功能: 设计一个基于FPGA…...
攻防世界web篇-backup
这是链接中的网页,只有一句话 试着使用.bak点缀看看是否有效 这里链接中加上index.php.bak让下在东西 是一个bak文件,将.bak文件改为.php文件试试 打开.php文件后就可以得到flag值...
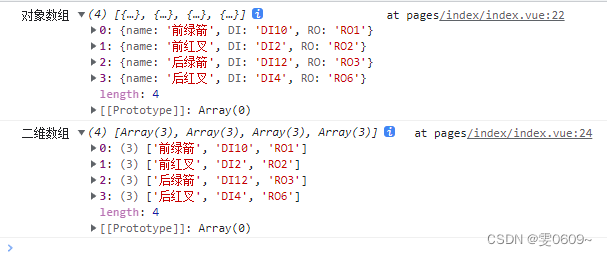
uni-app:js二维数组与对象数组之间的转换
一、二维数组整理成对象数组 效果 [ ["前绿箭","DI10","RO1"], ["前红叉","DI2","RO2"], ["后绿箭","DI12","RO3"], ["后红叉","DI4","RO6"] ] …...

15-bean生命周期,循环依赖
文章目录 1. bean生命周期 1. bean生命周期...

缩短cin时间
std::ios::sync_with_stdio(false);...

【试题030】C语言之关系表达式例题
1.关系表达式是用关系运算符将两个表达式连接起来 错误示例:a<bc (不是关系运算符,是赋值运算符) 2.题目:设int m160,m280,m3100;,表达式m3>m2>m1的值是 ? 3.代码分析: …...
ArGIS Engine专题(14)之GP模型根据导入范围与地图服务相交实现叠置分析
一、结果预览 二、需求简介 前端系统开发时,可能遇到如下场景,如客户给出一个图斑范围,导入到系统中后,需要判断图斑是否与耕地红线等地图服务存在叠加,叠加的面积有多少。虽然arcgis api中提供了相交inserect接口,但只是针对图形几何之间的相交,如何要使用该接口,则需…...
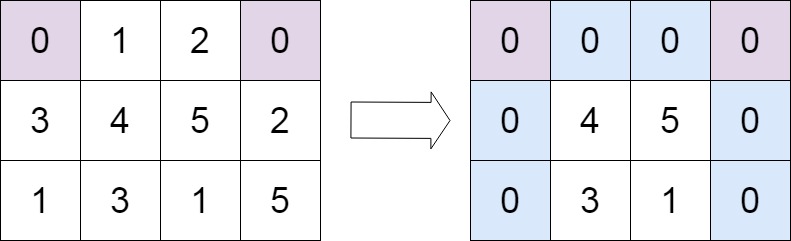
矩阵置零(C++解法)
题目 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例 1: 输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]示例 2: 输入…...

Ansible的debug模块介绍,fact变量采集和缓存相关操作演示
目录 一.debug模块的使用方法 1.帮助文档给出的示例 2.主要用到的参数 (1)msg:主要用这个参数来指定要输出的信息 (2)var:打印指定的变量,一般是通过register注册了的变量 (3&…...
零基础新手也能会的H5邀请函制作教程
随着科技的的发展,H5邀请函已经成为了各种活动、婚礼、会议等场合的常见邀约方式。它们不仅可以提供动态、互动的体验,还能让邀请内容更加丰富多彩。下面,我们将通过乔拓云平台,带领大家一步步完成H5邀请函的制作。 1. 选择可靠的…...

推荐《中华小当家》
《中华小当家!》 [1] 是日本漫画家小川悦司创作的漫画。该作品于1995年至1999年在日本周刊少年Magazine上连载。作品亦改编为同名电视动画,并于1997年发行播出。 时隔20年推出续作《中华小当家!极》,于2017年11月17日开始连载。…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

