数据结构中的七大排序(Java实现)
目录
一、直接插入排序
二、希尔排序
三、直接选择排序
四、堆排序
五、冒泡排序
六、快速排序
七、归并排序
一、直接插入排序
思想:
定义i下标之前的元素全部已经有序,遍历一遍要排序的数组,把i下标前的元素全部进行排序,当遍历玩这个数组后,就已经排好序了。
代码如下:
public static void insertSort(int[] array) {for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i - 1;for(; j >= 0;; j--) {if(array[j] > tmp) {array[j + 1] = array[j];} else {break;}}array[j + 1] = tmp;}}代码解析
要使i下标之前的元素都有序,定义一个j下标,为i - 1;再用tmp记录i下标的位置,只要j下标元素比tmp大,j下标的元素就要放到j+1下标,最后j走完后,再把最小的tmp放在j+1位置。
时间复杂度、空间复杂度、稳定性:
时间:O(n^2)
空间:O(1)
稳定性:稳定
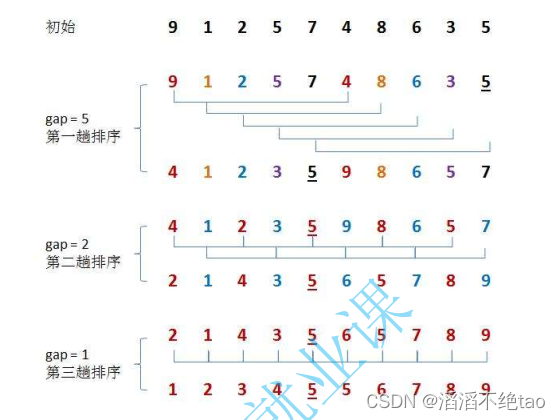
二、希尔排序
思想:
希尔排序也称缩小增量排序,就是分次去进行排序,越排到后面就会越有序,每次间隔是gap,然后逐渐缩小,到最后间隔为0,也就是用我们的直接插入排序,数组越有序,速度也会越快。那么就很简单了,我们只需改一下直接插入排序每次排序的间隔,把他们分成不同组进行排序,直到最后间隔为0,就只剩一组,然后也是用直接插入排序,做最后一次排序,排完就是有序的了。
图式例:
代码如下:
public static void shellSort(int[] array) {int gap = array.length / 2;while (gap >= 1) {gap /= 2;shell(array, gap);}}public static void shell(int[] array, int gap) {for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i - gap;for(; j >= 0; j -= gap) {if(array[j] > tmp) {array[j + gap] = array[j];} else {break;}}array[j + gap] = tmp;}}时间复杂度、空间复杂度、稳定性:
时间:n^1.3(严蔚敏) 因为gap取值方式不同,计算出来的时间复杂度也会不同
空间:O(1)
稳定性:不稳定
三、直接选择排序
思想:
直接选择排序也是和直接插入排序差不多,定义i下标前的元素全部都有序,不过排序的方式不同,它是拿i下标前的元素和i下标后的元素进行比较,找到下标最小的元素,把最小元素放进i下标中,同时这个i下标元素放到被这个最小下标位置。
代码实现:
public static void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIndex = i;//记录最小值的下标for (int j = i+1; j < array.length; j++) {if(array[j] < array[minIndex]) {minIndex = j;}}//走完这里,找到最小元素的下标minIndex//交换int tmp = array[i];array[i] = array[minIndex];array[minIndex] = tmp;}}时间复杂度、空间复杂度、稳定性:
时间:O(n^2)
空间:O(1)
稳定性:不稳定
四、堆排序
思想:
堆其实就是完全二叉树,下标是从上到下,从左到右依次递增,要把堆排序成升序,就要把他先变成大根堆,每次出大根堆的顶点,把顶点放在最后一个节点,然后再向下调整一次,第二次把大根堆的顶点放到倒数第二个位置,依次往后推。
代码实现:
//堆排序public static void heapSort(int[] array) {//先转换成大根堆createHeap(array);//开始换,然后向下转换for (int i = array.length - 1; i > 0 ; i--) {//i下标的节点和堆顶交换int tmp = array[0];array[0] = array[i];array[i] = tmp;//向下调整siftDown(array,0, i);}}
//创建大根堆public static void createHeap(int[] array) {//从最后一个父节点开始向下调整,下标依次往前减//parent = (child - 1) / 2; 左:child = parent * 2 + 1 右:child = parent * 2 + 2for (int i = (array.length - 1 - 1) / 2; i >= 0 ; i--) {siftDown(array, i, array.length);}}//向下调整public static void siftDown(int[] array, int parent, int length) {//定义一个child为该父节点的左孩子int child = parent * 2 + 1;while (child < length) {//比较改父节点的左右孩子,把值最大的孩子作为交换节点if(array[child] < array[child + 1]) {child += 1;}//比较父节点和孩子节点大小if(array[parent] < array[child]) {//交换int tmp = array[parent];array[parent] = array[child];array[child] = tmp;parent = child;child = child * 2 + 1;} else {break;}}}时间复杂度、空间复杂度、稳定性:
时间复杂度:O(NlogN)
空间复杂度:O(1)
稳定性:不稳定
五、冒泡排序
思想:
冒泡排序的思想很简单,就是第一次把最大的值放到数组最后一个下标中,再把第二大的元素放到数组倒数第二个下标中,依次类推
代码实现:
//冒泡排序public static void bubbleSort(int[] array) {for (int i = 0; i < array.length; i++) {boolean flag = false;//标记for (int j = 0; j < array.length - 1 - i; j++) {if(array[j] > array[j + 1]) {//交换int tmp =array[j];array[j] = array[j + 1];array[j + 1] = tmp;flag = true;}}if(!flag) {break;}}}时间复杂度、空间复杂度、稳定性:
时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:稳定
六、快速排序
思想:
使用递归思想(也可以采用非递归思想),把一组数据划分成两部分,左边都小于该下标元素,右边都大于该下标元素,再在左边去找元素划分,右边元素去划分,依次往后推,直到左右两边都没有元素可以划分了,就是只剩一个元素了,这时候往回倒,就有序了
代码实现:
public static void quickSort(int[] array) {int left = 0;int right = array.length - 1;quick(array, left, right);}public static void quick(int[] array, int start, int end) {//递归结束条件if(start >= end) {return;}int pivot = partition(array, start, end);quick(array, start, pivot - 1);quick(array, pivot + 1, end);}public static int partition(int[] array, int left, int right) {//找到一个下标元素,左边都比这个下标元素小,右边都比这个下标元素大,并且还要返回这个下标//记录下标为0的值,放在tmp中int tmp = array[0];while (left < right) {//先走右边if(left < right && array[right] >= tmp) {right--;}if(left < right && array[left] <= tmp) {left++;}//左下标的值大于tmp,右下标的值小于tmp,这两个下标值交换int newTmp = array[left];array[left] = array[right];array[right] = newTmp;}//走到这,left和right相遇了,left下标的值和tmp交换,并且返回这个位置的下标int newTmp = tmp;tmp = array[left];array[left] = newTmp;return left;}
时间复杂度、空间复杂度、稳定性:
时间复杂度:O(NlogN)
空间复杂度:O(logN~N)
稳定性:不稳定
七、归并排序
思想:
将一组数组分割成左右两部分,和快速排序找出的中件位置不同,归并的中间位置是最左和最右下标相加再除2(left+right)/ 2,运用的也是递归思想(也可以采用非递归思想),采用分治法,一直找到最左边进行排序,然后再找最右边进行排序,再往归回整体排序(合并),合并的时候是放在一个临时数组中,再把这个临时数组拷贝到原数组,下标要对应
代码实现:
public static void mergeSort(int[] array) {int start = 0;int end = array.length - 1;mergeSortFunc(array, start, end);}//套壳public static void mergeSortFunc(int[] array, int start, int end) {//递归结束标志if(start >= end) {return;}//求出中间节点位置int mid = (start + end) / 2;//左边mergeSortFunc(array, start, mid);//右边mergeSortFunc(array, mid + 1, end);//合并merge(array, start, mid, end);}//合并public static void merge(int[] array, int left, int mid, int right) {//定义mid两边的左右下标int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;//定义一个新的数组,存放array排序完后的数组int[] tmpArray = new int[right - left - 1];int k = 0;while (s1 <= e1 && s2 <= e2) {//比较左右两边s1和s2的值if(array[s1] < array[s2]) {tmpArray[k++] = array[s1++];} else {tmpArray[k++] = array[s2]++;}if(s1 <= e1) {tmpArray[k++] = array[s1++];}if(s2 <= e2) {tmpArray[k++] = array[s2++];}}//拷贝到原数组for (int i = 0; i < tmpArray.length; i++) {array[left + i] = tmpArray[i];}}时间复杂度、空间复杂度、稳定性:
时间复杂度:O(NlogN)
空间复杂度:O(N)
稳定性:不稳定
都看到这了,给个免费的赞呗,谢谢谢谢!!!
相关文章:
数据结构中的七大排序(Java实现)
目录 一、直接插入排序 二、希尔排序 三、直接选择排序 四、堆排序 五、冒泡排序 六、快速排序 七、归并排序 一、直接插入排序 思想: 定义i下标之前的元素全部已经有序,遍历一遍要排序的数组,把i下标前的元素全部进行排序࿰…...

深度学习基础算法
算法 1.K近邻算法 机器学习--K-近邻算法(KNN)_k近邻-CSDN博客 2. 数据库样本: CIFAR-10 CIFAR-10数据集(介绍、下载读取、可视化显示、另存为图片)_cifar10数据集-CSDN博客...
-- ir - 红外遥控)
LuatOS-SOC接口文档(air780E)-- ir - 红外遥控
ir.sendNEC(pin, addr, cmd, repeat, disablePWM)# 发送NEC数据 参数 传入值类型 解释 int 使用的GPIO引脚编号 int 用户码(大于0xff则采用Extended NEC模式) int 数据码 int 可选,引导码发送次数(110ms一次࿰…...
Java虚拟机常见面试题总结
梳理Java虚拟机相关的面试题,主要参考《深入理解Java虚拟机 JVM高级特性与最佳实践》(第2版, 周志明 著)一书,其余部分整合网络相关内容。注意,关于Java并发编程的面试题因为内容较多,单独整理。Java基础相关的面试题可以参考Java…...
NVIDIA NCCL 源码学习(十一)- ring allreduce
之前的章节里我们看到了nccl send/recv通信的过程,本节我们以ring allreduce为例看下集合通信的过程。整体执行流程和send/recv很像,所以对于相似的流程只做简单介绍,主要介绍ring allreduce自己特有内容。 单机 搜索ring 在nccl初始化的过…...

前端--性能优化【上篇】--网络优化与页面渲染优化
一、网络优化 1、DNS预解析 link标签的rel属性设置dns-prefetch,提前获取域名对应的IP地址 2、CDN(网络分发系统) 用户与服务器的物理距离对响应时间也有影响。 内容分发网络(CDN)是一组分散在不同地理位置的 web…...

git 删除分支
目录 1,查看分支2,删除本地分支3,删除远程分支 1,查看分支 # 查看本地分支 git branch# 查看远程分支 git branch -r# 查看所有分支 git branch -a2,删除本地分支 # -d 是 --delete 的简写,会在删除前检查…...

SQLite Write-ahead Logging
1. 概述2. WAL如何工作 2.1 检验指示(Checkpointing)2.2 并发性(Concurrency)2.3 性能考虑(Performance Considerations)3. 激活并配置WAL模式 3.1 自动checkpoint3.2 应用开始的checkpoint3.3 WAL模式的持久性4. 只读数据库5. 避免过大的WAL文件6. WAL索引的共享内存应用7. 不…...

手机有什么爬虫App工具?
随着智能手机的普及和应用的繁盛,越来越多的人开始对手机App进行数据爬取和分析。那么,在进行手机App爬虫的过程中,我们可以借助哪些工具呢?让我们一起来了解一下吧! 1、Fiddler Fiddler是一款功能强大的网络调试工具…...

290_C++_截取的一部分FTP视频上传代码,任务信息中读取视频帧数据并将其提供给 libcurl 用于上传。
1、这些结构体和枚举类型的设计是为了在上传过程中有效地存储和传递不同类型的任务信息,以便在上传操作中使用这些信息来管理和跟踪不同类型的上传任务。它们提供了不同类型上传任务所需的特定信息和状态变量 enum UploadTaskType {UTT_Common,UTT_Video };struct UploadInfo…...

读《Gaitset: Regarding gait as a set for cross-view gait recognition》
2019在AAAI(还有一版叫GaitSet: Regarding Gait as a Set for Cross-View Gait Recognition,大体上一样) 摘要 现有的步态识别方法要么利用步态模板,难以保存时间信息,要么利用保持不必要的顺序约束的步态序列&#x…...

驱动实现LED点灯
demo.c #include <linux/init.h> #include <linux/module.h> #include <linux/fs.h> #include <linux/uaccess.h> #include <linux/io.h> #include "head.h" //定义三个指针指向映射后的虚拟内存 unsigned int *vir_moder; unsigned …...
【Reinforcement Learning】Ubuntu中mujoco210 mujoco_py D4RL安装及错误解决
Ubuntu中mujoco210 mujoco_py D4RL安装及错误解决 本文根据一篇知乎文章链接在此进行配置,记录在配置过程中遇到的一些问题,原文作者的教程很详细,在此对原作者表示感谢~ 直接进行知乎原文的第2.2 有效安装过程(避坑) 2.注意上…...
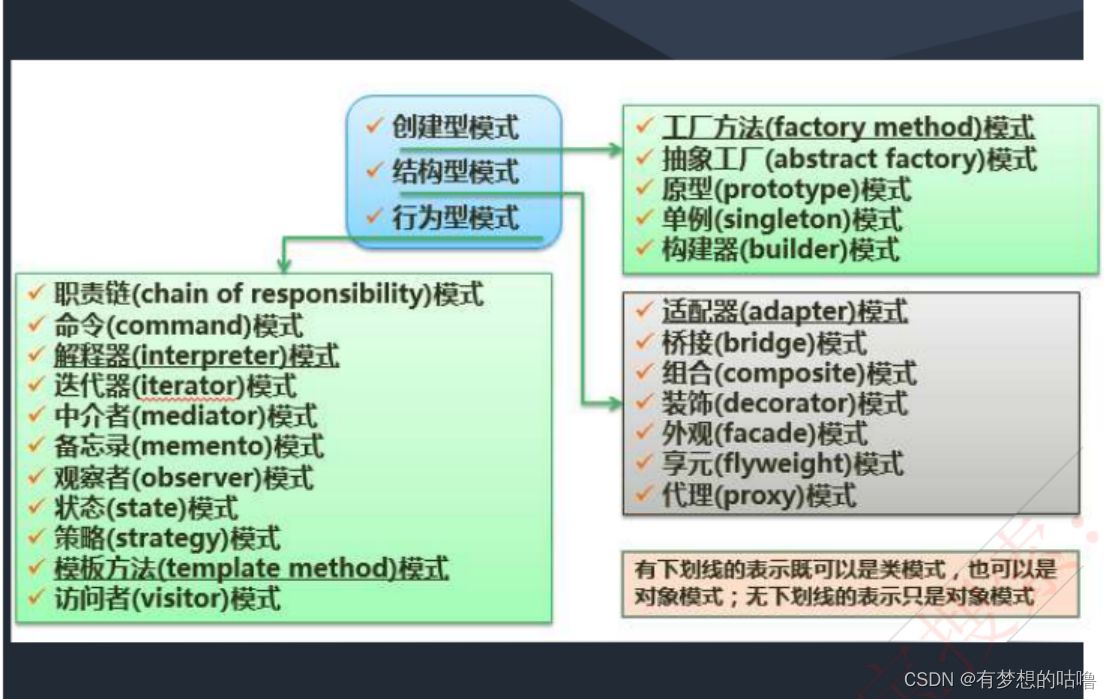
设计模式截图记录
设计模式截图记录...
)
代碼隨想錄算法訓練營|第三十九天|738.单调递增的数字、968.监控二叉树、第八章 贪心算法總結。刷题心得(c++)
目录 讀題 738.单调递增的数字 自己看到题目的第一想法 看完代码随想录之后的想法 968.监控二叉树 自己看到题目的第一想法 看完代码随想录之后的想法 738.单调递增的数字 - 實作 思路 Code 968.监控二叉树 - 實作 思路 Code 贪心算法 總結 贪心理论基础 貪心…...

前言:自动化框架的设计模式
1、UI自动化框架的设计模式 自动化测试框架有很多种,常见的自动化框架分类如下: 在使用上面的自动化框架时,通常会结合使用分层思想,也就是一些自动化框架设计模式,今天重点分享一下UI自动化框架设计使用比较多的一种…...

Web架构安全分析/http/URL/Cookie攻击
Web 架构安全分析 Web 工作机制及基本概念 传统 Web 架构 LAMP 网页 概念 网页就是我们可以通过浏览器上网看到的精美页面,一般都是经过浏览器渲染过的 .html 页面,html 语言在浏览器中渲染。其中包含了CSS、JavaScript 等前端技术。通过浏览器访问…...

.git 目录中有什么?
好吧,我想你们中的大多数人每天都或多或少地使用 git,但是您是否研究过 git 创建的 .git 文件夹中的内容?本文[1]我们将一起探索一下,了解里面到底发生了什么。 ❝ git 在基本层面上只是一堆通过文件名相互链接的文本文件。 ❞ in…...

Debian11系统简单配置
debian11系统简单配置 网卡配置 修改/etc/network/interfaces address 192.168.0.188 gateway 192.168.0.1 netmask 255.255.255.0重启网卡systemctl restart networking.service systemctl restart networking 执行apt 报错 rootdebian:~# apt update 忽略:1 cdrom://[D…...

家装、家居两不误,VR全景打造沉浸式家装体验
当下,用户对生活品质要求日益提升,越来越多的用户对多功能家装用品需求较大,由此造就了VR全景家装开始盛行。VR全景家装打破传统二维空间模式,通过视觉、交互等功能让用户更加真实、直观的体验和感受家居布置的效果。 一般来说&am…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
