【算法训练-回溯算法 零】回溯算法解题框架
抽象地说,解决一个回溯问题,实际上就是遍历一棵决策树的过程,树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍,把叶子节点上的答案都收集起来,就能得到所有的合法答案。站在回溯树的一个节点上,你只需要思考 3 个问题:
- 路径:也就是已经做出的选择。
- 选择列表:也就是你当前可以做的选择。
- 结束条件:也就是到达决策树底层,无法再做选择的条件。
回溯算法的框架:
回溯算法框架代码
以下就是回溯算法的框架代码
result = []
def backtrack(路径, 选择列表):if 满足结束条件:result.add(路径)returnfor 选择 in 选择列表:做选择backtrack(路径, 选择列表)撤销选择其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」
排列、组合、子集
无论是排列、组合还是子集问题,简单说无非就是让你从序列 nums 中以给定规则取若干元素,主要有以下几种变体:
- 元素无重不可复选【I】,即 nums 中的元素都是唯一的,每个元素最多只能被使用一次,这也是最基本的形式。以组合为例,如果输入 nums = [2,3,6,7],和为 7 的组合应该只有 [7]。
- 元素可重不可复选【II】,即 nums 中的元素可以存在重复,每个元素最多只能被使用一次。以组合为例,如果输入 nums = [2,5,2,1,2],和为 7 的组合应该有两种 [2,2,2,1] 和 [5,2]。
- 元素无重可复选,即 nums 中的元素都是唯一的,每个元素可以被使用若干次。以组合为例,如果输入 nums = [2,3,6,7],和为 7 的组合应该有两种 [2,2,3] 和 [7]。
当然,也可以说有第四种形式,即元素可重可复选。但既然元素可复选,那又何必存在重复元素呢?元素去重之后就等同于形式三,所以这种情况不用考虑。
排列
排列的概念和排列树
排列的概念
全排列是一个组合数学概念,它指的是一个给定集合中所有元素的不同排列方式【不同顺序是两个】。全排列是一个重要的排列组合问题,通常用于解决诸如排列、组合、密码学和计算机算法等领域的问题。
假设有一个集合,其中包含n个不同的元素,全排列就是这些元素的所有可能的排列方式。每个元素在每个排列中都只出现一次。全排列问题通常用于计算和枚举这些排列,以便解决各种问题,如密码破解、计算机编程中的排列操作等。
在数学符号中,全排列通常用符号P(n)来表示,其中n表示集合中元素的数量。因此,对于上述例子,P(3) = 3! = 3 × 2 × 1 = 6。全排列的数量等于元素个数的阶乘。
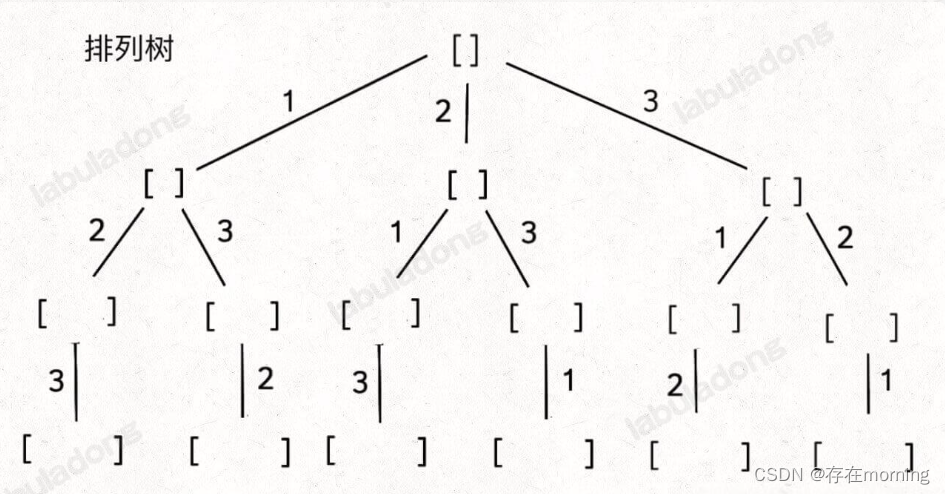
排列树
排列树如下
子集
子集的概念和子集树
子集的概念
组合问题和子集问题其实是等价的,什么是子集呢?子集是集合论中的一个重要概念,它指的是一个集合中的部分元素的集合。更具体地说,如果集合A中的所有元素都包含在集合B中,那么A是B的一个子集。这可以用符号表示为A ⊆ B。
以下是子集的一些关键特点和定义:
-
子集关系:如果集合A的任意一个元素都是集合B的元素,那么集合A称为集合B的子集
-
空集合是任何集合的子集:空集合(不包含任何元素的集合)是所有集合的子集。形式化地,∅(空集合)是任何集合A的子集,即∅ ⊆ A。
-
集合是其自身的子集:任何集合都是其自身的子集,即对于任何集合A,A ⊆ A。
-
真子集:如果A是B的子集,但A和B不相等,那么A被称为B的真子集。形式化地,如果A ⊆ B 且 A ≠ B,那么A是B的真子集,可以表示为A ⊂ B。
例如,假设有两个集合:
A = {1, 2}
B = {1, 2, 3, 4}
在这种情况下,集合A是集合B的子集,因为A中的所有元素都包含在B中。所以,A ⊆ B。同时,A也是B的真子集,因为它们不相等,即A ≠ B,可以表示为A ⊂ B。
子集树
子集树如下
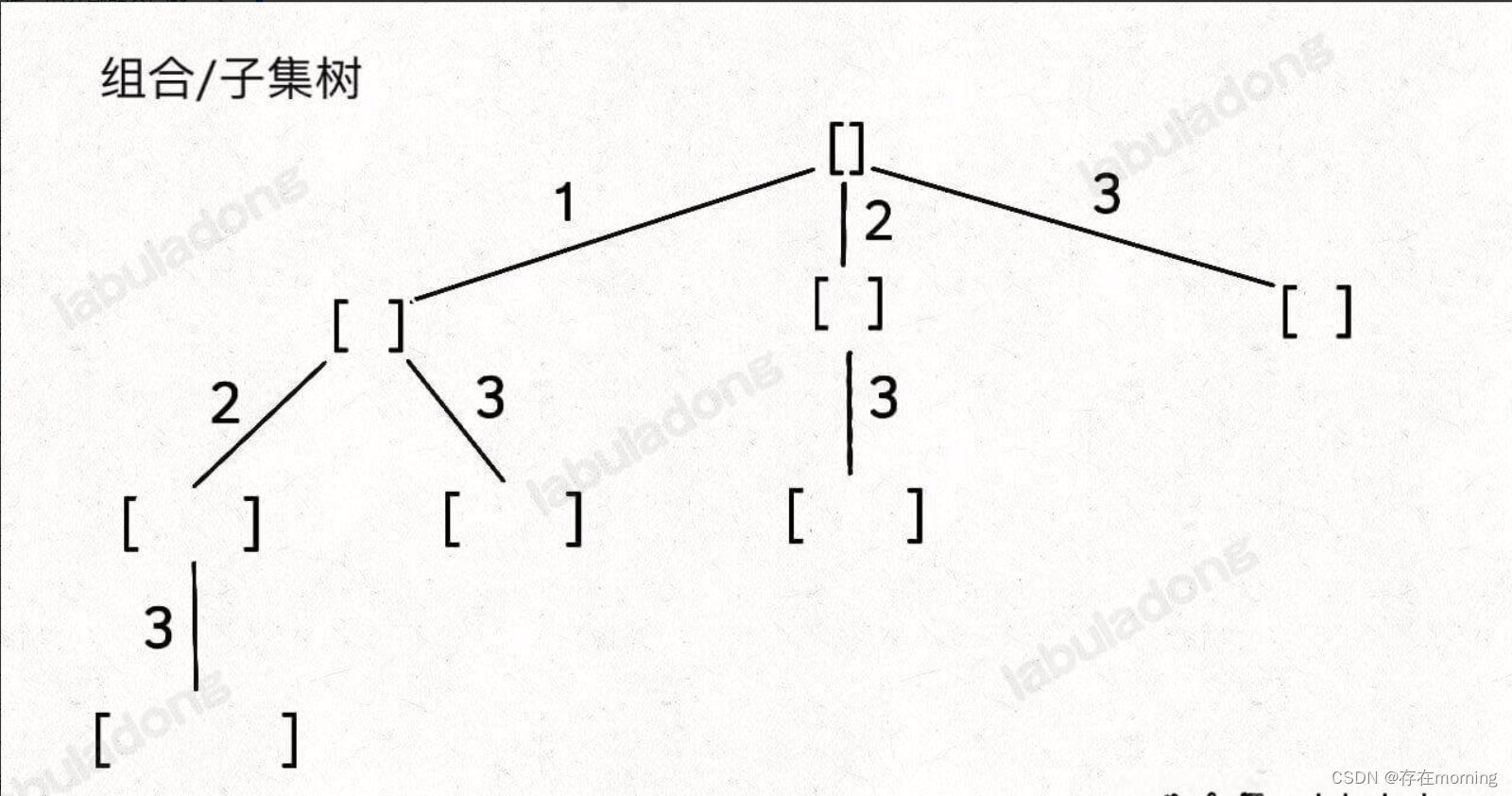
所有子集,就是把所有节点的值都收集起来
组合
组合的概念和组合树
组合的概念
组合是组合数学中的一个重要概念,它涉及从给定的集合中选择出一定数量的元素,而不考虑元素的顺序。组合用来计算在不同的选择中,选取一组元素的方式,而不考虑它们的排列顺序。组合通常表示为 “C(n, k)”,其中 “n” 表示集合中的元素数量,“k” 表示要选择的元素数量。
组合的定义如下:
在集合中,从n个不同的元素中选择k个元素,其中1 ≤ k ≤ n,这种选择方式称为一个组合。组合通常用 “C(n, k)” 表示,其中 “n” 是总元素数量, “k” 是选择的元素数量。组合的数量可以用以下公式计算:
C(n, k) = n! / (k!(n-k)!)
其中 “n!” 表示n的阶乘,即n的所有正整数的乘积。
组合与排列不同,排列考虑元素的顺序,而组合仅考虑元素的选择,无论其顺序如何。例如,如果有一个集合 {A, B, C},那么从中选择两个元素的组合有三种:{A, B}、{A, C} 和 {B, C},而不考虑元素的排列顺序。
组合的应用非常广泛,包括在组合优化、统计学、概率论、密码学、计算机科学和组合数学等领域。
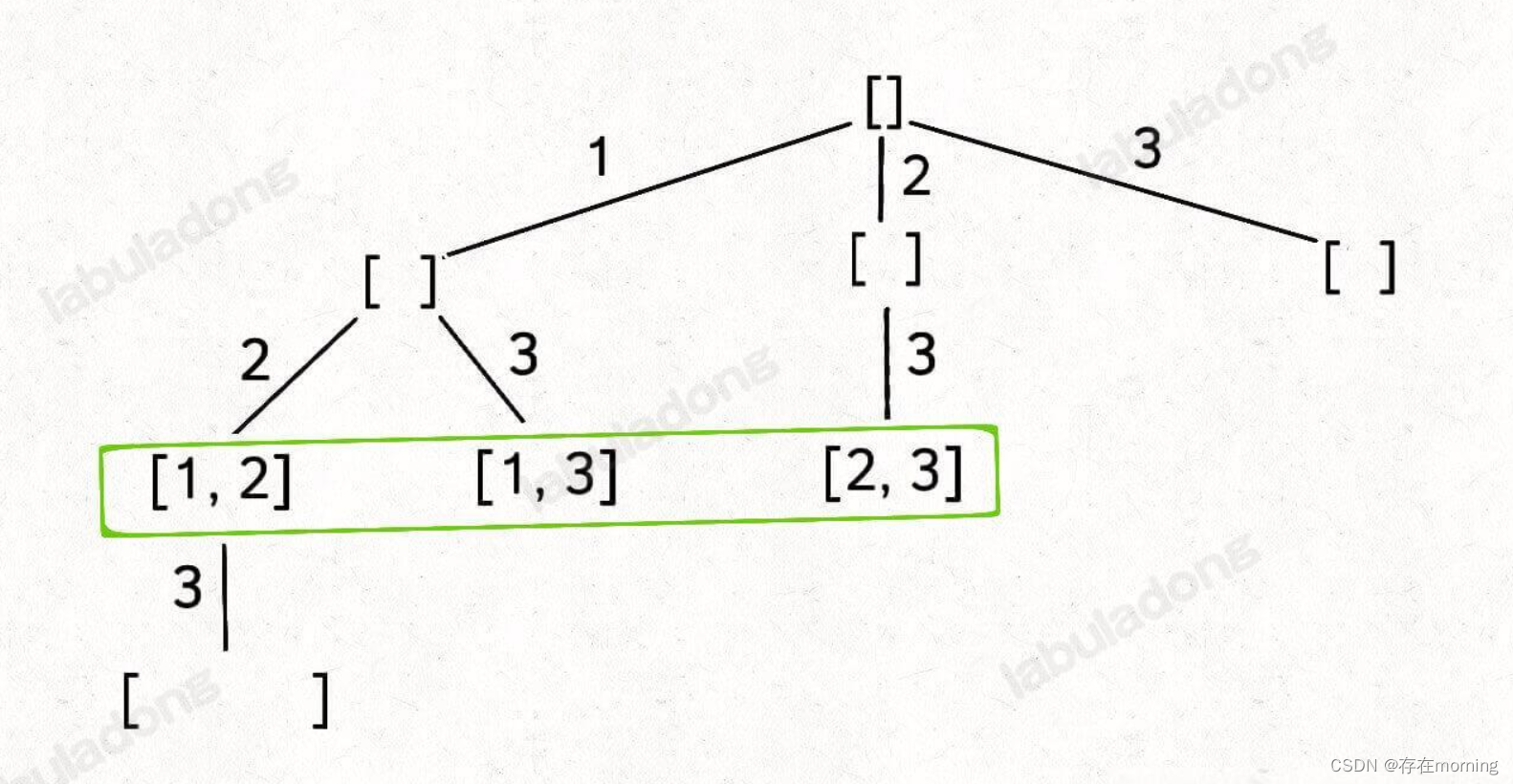
组合树
组合树与子集树相同,只不过是子集树上满足条件的某一层节点
排列、子集、组合的区别和联系
下表是排列、子集和组合的联系与区别的简要总结:
| 特点 | 排列(Permutation) | 子集(Subset) | 组合(Combination) |
|---|---|---|---|
| 定义 | 考虑元素的排列顺序 | 不考虑元素的排列顺序 | 不考虑元素的排列顺序 |
| 选择元素个数(k) | k个元素 | 0到n个元素 | k个元素 |
| 顺序重要性 | 重要 | 不重要 | 不重要 |
| 表示形式 | P(n, k) | - | C(n, k) |
| 计算公式 | n! / (n-k)! | - | n! / (k!(n-k)!) |
| 例子 | 排列一组车辆的顺序 | 集合中的元素的所有可能子集 | 从一组学生中选择小组 |
这个表格总结了排列、子集和组合的定义、特点、选择元素个数、顺序重要性、表示形式和计算公式,以帮助理解它们之间的联系和区别。
相关文章:

【算法训练-回溯算法 零】回溯算法解题框架
抽象地说,解决一个回溯问题,实际上就是遍历一棵决策树的过程,树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍,把叶子节点上的答案都收集起来,就能得到所有的合法答案。站在回溯树的一个节点上,你…...

GAN.py
原代码地址:github.com/zqhang/MTGFLOW 目录 def ConvEncoder() def ConvDecoder() class CNNAE(torch.nn.Module): class R_Net(torch.nn.Module): class D_Net(torch.nn.Module): def R_Loss() def D_Loss()…...
C语言动态内存管理
1.为什么要动态内存分配? int val 20; int a[10]{0};上面我们声明并定义了一个大小为4字节的整型变量,一个容量为10*4字节的整型数组。 开辟方式:我们在栈上开辟。 开辟空间的方式有两个特点: 1. 空间开辟 大小是固定 的。 2. 数组在申明…...
)
小红书商品详情API接口(商品详情页面数据接口)
小红书商品详情API接口(商品详情页面数据接口 小红书商品详情API接口(商品详情页面数据接口)代码对接如下: 1.公共参数 名称类型必须描述keystring是get请求方式拼接在url中,点击获取api_namestring是 api接口名称cachestrin…...

nginx配置文件的内容解释和简化方案
文章目录 配置文件内容理解配置文件精简nginx.confapp1.conf 配置文件内容理解 events {worker_connections 1024; }http {include mime.types;default_type application/octet-stream;sendfile on;keepalive_timeout 65;client_max_body_size 50m;client…...
)
Java设计模式之访问者模式(Visitor Pattern)
访问者模式(Visitor Pattern)是一种行为型设计模式,它允许在不修改现有对象结构的情况下定义新的操作。该模式将操作封装在一个访问者对象中,使得可以在不改变被访问对象的类的前提下,通过访问者对象对被访问对象进行新…...
others-AppLovin广告接入
title: others-AppLovin广告接入 categories: Others tags: [广告, AppLovin] date: 2023-10-20 10:07:01 comments: false mathjax: true toc: true others-AppLovin广告接入 前篇 官方 - https://www.applovin.com/ Android sdk - https://github.com/AppLovin/AppLovin-MAX…...
ESP32集成开发环境Espressif-IDE安装 – Windows
陈拓 2023/10/15-2023/10/16 1. 概述 Espressif IDE是一个基于Eclipse CDT的集成开发环境(IDE),用于使用ESP-IDF框架开发物联网应用程序。这是一个专门为ESP-IDF构建的独立定制IDE。Espressif IDE附带了IDF Eclipse插件、重要的Eclipse CDT插…...

python之if else语句介绍
python之if else语句介绍 在Python中,if和else是两种重要的控制流语句,它们用于根据特定的条件来执行不同的代码块。以下是它们的用法和详细介绍: 1)if语句 if语句用于在满足某种条件时执行特定的代码块。它的基本语法如下&#…...
Java版ORM最初雏形
经过一个晚上的加班,终于把ORM初步结构工程搭好了。工程依赖有点难用,编辑器提示比VS差很多。 首先LIS.Core创建一个最初的容器雏形,先能反射得到对象给ORM获得数据库驱动 然后ORM创建数据库驱动差异接口,不同数据库实现接口后配…...
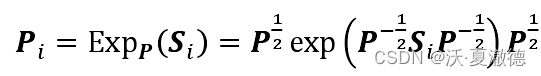
黎曼几何与切空间之间的投影
公式: 从黎曼空间投影到切空间,其中P为黎曼均值,也是切空间的参考中心点,Pi是要投影到切空间的点。 从切空间投影回来,其中Si为切空间中的向量。 function Tcov CovToTan(cov,Mcov)Cm12 Mcov^(-1/2);X_new logm(Cm…...
【Tomcat】为Tomcat服务配置本地Apr库以提升性能
关于 apr 和 apr-util 对 Tomcat 服务的性能提升的说明: 要测APR给tomcat带来的好处最好的方法是在慢速网络上(模拟Internet),将Tomcat线程数开到300以上的水平,然后模拟一大堆并发请求。如果不配APR,基本…...

普通人在当前大环境下——少看宏观,多看具体
前言 宏观叙事,简而言之,就是从宏观把握历史社会的发展,寻找其中永恒的共性。我们大概听过此类的话:贸易战导致本地经济下滑、气候变化是因为过去几十年的工业发展、大环境不行导致不赚钱。此类叙事方式,身边人聊的甚欢,在媒体、社交圈、日常社群交流中,随处可见。以前…...

用echarts在vue2中实现3d饼图
先看效果,再看文章: 一、安装插件 3d的图不仅用到echarts,还用到了echarts-gl,因此都需要安装一下哦~ npm install echarts npm install echarts-gl2.0.9 //可以指定版本,也可不指定二、在main.js中引入 import * …...
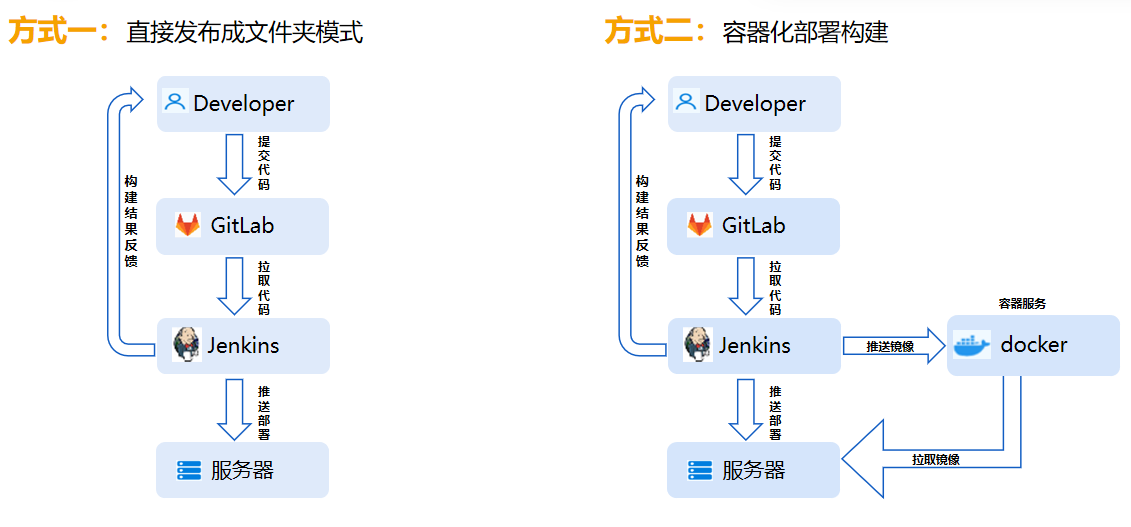
低代码助力软件开发
低代码开发工具正在日益变得强大,它正不断弥合着前后端开发之间的差距。对于后端来说,基于低代码平台开发应用时,完全不用担心前端的打包、部署等问题,也不用学习各种框架(Vue、React、Angular等等)&#x…...

C嘎嘎之类和对象上
> 作者简介:დ旧言~,目前大二,现在学习Java,c,c,Python等 > 座右铭:松树千年终是朽,槿花一日自为荣。 > 目标:掌握类的引用和定义,熟悉类成员函数的…...
Vue 3使用 Iconify 作为图标库与图标离线加载的方法、 Icones 开源在线图标浏览库的使用
之前一直naive-ui搭配使用的是xicons,后来发现Iconify支持的图标合集更多,因此转而使用Iconify。 与FontAwesome不同的是,Iconify配合Icones相当于是一个合集,Iconify提供了快捷引入图标的方式,而Icones是一个大的图标…...
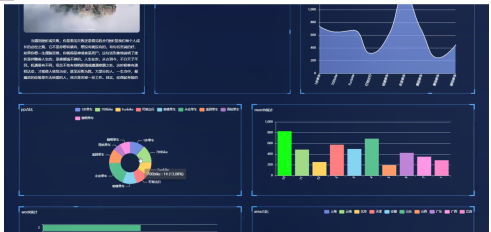
springboot+vue基于Spark的共享单车数据存储系统的设计与实现【内含源码+文档+部署教程】
博主介绍:✌全网粉丝10W,前互联网大厂软件研发、集结硕博英豪成立工作室。专注于计算机相关专业毕业设计项目实战6年之久,选择我们就是选择放心、选择安心毕业✌ 🍅由于篇幅限制,想要获取完整文章或者源码,或者代做&am…...

如何使双核心的ESP32开启双核功能同时执行多任务
如何使双核心的ESP32开启双核功能同时执行多任务 简介查看ESP32当前哪一个内核在执行任务双核同时执行任务总结 简介 ESP32-WROOM-32模组内置两个低功耗 Xtensa 32-bit LX6 MCU,两个 CPU 核(core 0与core 1)可以被单独控制。可以在两个内核上…...
Node.js在Python中的应用实例解析
随着互联网的发展,数据爬取成为了获取信息的重要手段。本文将以豆瓣网为案例,通过技术问答的方式,介绍如何使用Node.js在Python中实现数据爬取,并提供详细的实现代码过程。 Node.js是一个基于Chrome V8引擎的JavaScript运行时环境…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
