最优化:建模、算法与理论(最优性理论2
5.7 约束优化最优性理论应用实例
5.7.1 仿射空间的投影问题
考虑优化问题
min x ∈ R n 1 2 ∣ ∣ x − y ∣ ∣ 2 2 , s . t . A x = b \min_{x{\in}R^n}\frac{1}{2}||x-y||_2^2,\\ s.t.{\quad}Ax=b x∈Rnmin21∣∣x−y∣∣22,s.t.Ax=b
其中 A ∈ R m × n , b ∈ R m , y ∈ R n A{\in}R^{m \times n},b{\in}R^m,y{\in}R^n A∈Rm×n,b∈Rm,y∈Rn为给定的矩阵和向量,这里不妨设矩阵A是行满秩的,这个问题可以看成仿射平面 { x ∈ R n ∣ A x = b } \{x{\in}R^n|Ax=b\} {x∈Rn∣Ax=b}的投影问题
对于等式约束,我们引入拉格朗日乘子 λ ∈ R m \lambda{\in}R^m λ∈Rm,构造拉格朗日函数
L ( x , λ ) = 1 2 ∣ ∣ x − y ∣ ∣ 2 + λ T ( A x − b ) L(x,\lambda)=\frac{1}{2}||x-y||^2+\lambda^T(Ax-b) L(x,λ)=21∣∣x−y∣∣2+λT(Ax−b)
因为只有仿射约束,估 S l a t e r Slater Slater条件满足, x ∗ x^* x∗为一个全局最优解,当且仅当存在 λ ∗ ∈ R m \lambda^*{\in}R^m λ∗∈Rm使得
{ x ∗ − y + A T λ = 0 A x ∗ = b \left\{ \begin{matrix} x^*-y+A^T\lambda=0\\ Ax^*=b \\ \end{matrix} \right. {x∗−y+ATλ=0Ax∗=b
由上述KKT条件第一式,等号左右两边同时左乘 A A A可得
A x ∗ − A y + A A T λ = 0 Ax^*-Ay+AA^T\lambda=0 Ax∗−Ay+AATλ=0
注意到 A x ∗ = b Ax^*=b Ax∗=b以及 A A T AA^T AAT是可逆矩阵,因此可以解出乘子
λ = ( A A T ) − 1 ( A y − b ) \lambda=(AA^T)^{-1}(Ay-b) λ=(AAT)−1(Ay−b)
代入回去可以得到
x ∗ = y − A T ( A A T ) − 1 ( A y − b ) x^*=y-A^T(AA^T)^{-1}(Ay-b) x∗=y−AT(AAT)−1(Ay−b)
5.7.2 线性规划问题
考虑线性规划问题
min x ∈ R n c T x , s . t . A x = b , x ≥ 0 (5.7.1) \min_{x{\in}R^n}{\quad}c^Tx,\\ s.t.{\quad}Ax=b,\\ x{\ge}0\tag{5.7.1} x∈RnmincTx,s.t.Ax=b,x≥0(5.7.1)
其中 A ∈ R m × n , b ∈ R m , c ∈ R n A{\in}R^{m \times n},b{\in}R^m,c{\in}R^n A∈Rm×n,b∈Rm,c∈Rn分别为给定的矩阵和向量
拉格朗日函数可以写为
L ( x , s , v ) = c T x + v T ( A x − b ) − s T x = − b T v + ( A T v − s + c ) T x , s ≥ 0 L(x,s,v)=c^Tx+v^T(Ax-b)-s^Tx\\ =-b^Tv+(A^Tv-s+c)^Tx,s{\ge}0 L(x,s,v)=cTx+vT(Ax−b)−sTx=−bTv+(ATv−s+c)Tx,s≥0
其中 s ∈ R n , v ∈ R m s{\in}R^n,v{\in}R^m s∈Rn,v∈Rm,由于线性规划是凸问题且满足 S l a t e r Slater Slater条件的,因此对于任意一个全局最优解 x ∗ x^* x∗,我们有如下KKT条件
{ c + A T v ∗ − s ∗ = 0 , A x ∗ = b x ∗ ≥ 0 s ∗ ≥ 0 s ∗ x ∗ = 0 (5.7.2) \left\{ \begin{matrix} c+A^Tv^*-s^*=0,\\ Ax^*=b \\ x^*{\ge}0\\ s^*{\ge}0\\ s^*x^*=0 \end{matrix} \right.\tag{5.7.2} ⎩ ⎨ ⎧c+ATv∗−s∗=0,Ax∗=bx∗≥0s∗≥0s∗x∗=0(5.7.2)
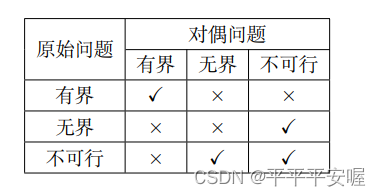
我们设原始问题和对偶问题最优解函数值分别为 p ∗ p^* p∗和 d ∗ d^* d∗,则根据 p ∗ p^* p∗取值情况,有如下三种可能
(1)如果 − ∞ < p ∗ < + ∞ ( 有界 ) -\infty<p^*<+\infty(有界) −∞<p∗<+∞(有界),那么原始问题可行而且存在最优解,由 S l a t e r Slater Slater条件知强对偶原理成立,因此有 d ∗ = p ∗ d^*=p^* d∗=p∗,即对偶问题也是可行的且存在最优解
(2)如果 p ∗ = − ∞ p^*=-\infty p∗=−∞,那么原始问题可行,但目标函数值无下界,由弱对偶原理知 d ∗ ≤ p ∗ = − ∞ d^*{\le}p^*=-\infty d∗≤p∗=−∞,即 d ∗ = − ∞ d^*=-\infty d∗=−∞,因为对偶问题是对目标函数极大化,所以此时对偶问题不可行
(3)如果 p ∗ = + ∞ p^*=+\infty p∗=+∞,那么原始问题无可行解,注意到 S l a t e r Slater Slater条件对原始问题不成立,此时对偶问题既可能是函数值无界( d ∗ = + ∞ d^*=+\infty d∗=+∞)也可能无可行解( d ∗ = − ∞ d^*=-\infty d∗=−∞),我们说,不可能出现 − ∞ < d ∗ < + ∞ -\infty<d^*<+\infty −∞<d∗<+∞的情形,这是因为如果对偶问题可行且存在最优解,那么可对对偶问题应用强对偶原理,进而导出原始问题也存在最优解,这矛盾了
5.7.3 基追踪
min x ∈ R n ∣ ∣ x ∣ ∣ 1 , s . t . A x = b (5.7.3) \min_{x{\in}R^n}||x||_1,\\ s.t.{\quad}Ax=b\tag{5.7.3} x∈Rnmin∣∣x∣∣1,s.t.Ax=b(5.7.3)
利用分解 x i = x i + − x i − x_i=x_i^+-x_i^- xi=xi+−xi−,其中 x i + = m a x { x i , 0 } , x i − = max { − x i , 0 } x_i^+=max\{x_i,0\},x_i^-=\max\{-x_i,0\} xi+=max{xi,0},xi−=max{−xi,0}分别表示 x x x的正部和负部,问题5.7.3的一种等价形式可以写成
min ∑ i x i + + x i − , s . t . A x + − A x − = b , x + , x − ≥ 0 \min{\sum_i}x_i^++x_i^-,\\ s.t.{\quad}Ax^+-Ax^-=b,\\ x^+,x^-{\ge}0 mini∑xi++xi−,s.t.Ax+−Ax−=b,x+,x−≥0
进一步的,令 y = [ x i + , x i − ] T ∈ R 2 n y=[x_i^+,x_i^-]^T{\in}R^{2n} y=[xi+,xi−]T∈R2n,我们将问题5.7.3转化为如下线性规划问题
min y ∈ R 2 n 1 T y , s . t . [ A , − A ] y = b , y ≥ 0 \min_{y{\in}R^{2n}}1^Ty,\\ s.t.{\quad}[A,-A]y=b,\\ y{\ge}0 y∈R2nmin1Ty,s.t.[A,−A]y=b,y≥0
其中 1 = ( 1 , 1 , ⋯ , 1 ) T ∈ R 2 n 1=(1,1,\cdots,1)^T{\in}R^{2n} 1=(1,1,⋯,1)T∈R2n
那么根据一般线性规划的最优性条件,等价于求解
{ 1 + [ A , − A ] T v ∗ − s ∗ = 0 , [ A , − A ] y ∗ = b y ∗ ≥ 0 s ∗ ≥ 0 s ∗ y ∗ = 0 (5.7.4) \left\{ \begin{matrix} 1+[A,-A]^Tv^*-s^*=0,\\ [A,-A]y^*=b \\ y^*{\ge}0\\ s^*{\ge}0\\ s^*y^*=0 \end{matrix} \right.\tag{5.7.4} ⎩ ⎨ ⎧1+[A,−A]Tv∗−s∗=0,[A,−A]y∗=by∗≥0s∗≥0s∗y∗=0(5.7.4)
同样的,我们也可以直接推导5.7.3的最优性条件,拉格朗日函数为
L ( x , v ) = ∣ ∣ x ∣ ∣ 1 + v T ( A x − b ) L(x,v)=||x||_1+v^T(Ax-b) L(x,v)=∣∣x∣∣1+vT(Ax−b)
x ∗ x^* x∗为全局最优解当且仅当存在 v ∗ ∈ R m v^*{\in}R^m v∗∈Rm使得
{ 0 ∈ ∂ ∣ ∣ x ∗ ∣ ∣ 1 + A T v ∗ , A x ∗ = b (5.7.5) \left\{ \begin{matrix} 0{\in}\partial||x^*||_1+A^Tv^*,\\ Ax^*=b \\ \end{matrix} \right.\tag{5.7.5} {0∈∂∣∣x∗∣∣1+ATv∗,Ax∗=b(5.7.5)
最优性条件5.7.4和5.7.5本质上是等价的
相关文章:

最优化:建模、算法与理论(最优性理论2
5.7 约束优化最优性理论应用实例 5.7.1 仿射空间的投影问题 考虑优化问题 min x ∈ R n 1 2 ∣ ∣ x − y ∣ ∣ 2 2 , s . t . A x b \min_{x{\in}R^n}\frac{1}{2}||x-y||_2^2,\\ s.t.{\quad}Axb x∈Rnmin21∣∣x−y∣∣22,s.t.Axb 其中 A ∈ R m n , b ∈ R m …...

redis一主一从搭建
1.复制一份redis.conf并将6380都改成6379 [redist3-dtpoc-dtpoc-web06 conf]$ cp redis.conf redis_6380.conf [redist3-dtpoc-dtpoc-web06 conf]$ vi redis_6380.conf port 6380 daemonize yes pidfile "/home/redis/redis/logs/redis_6380.pid" logfile "/hom…...
【MySql】8- 实践篇(六)
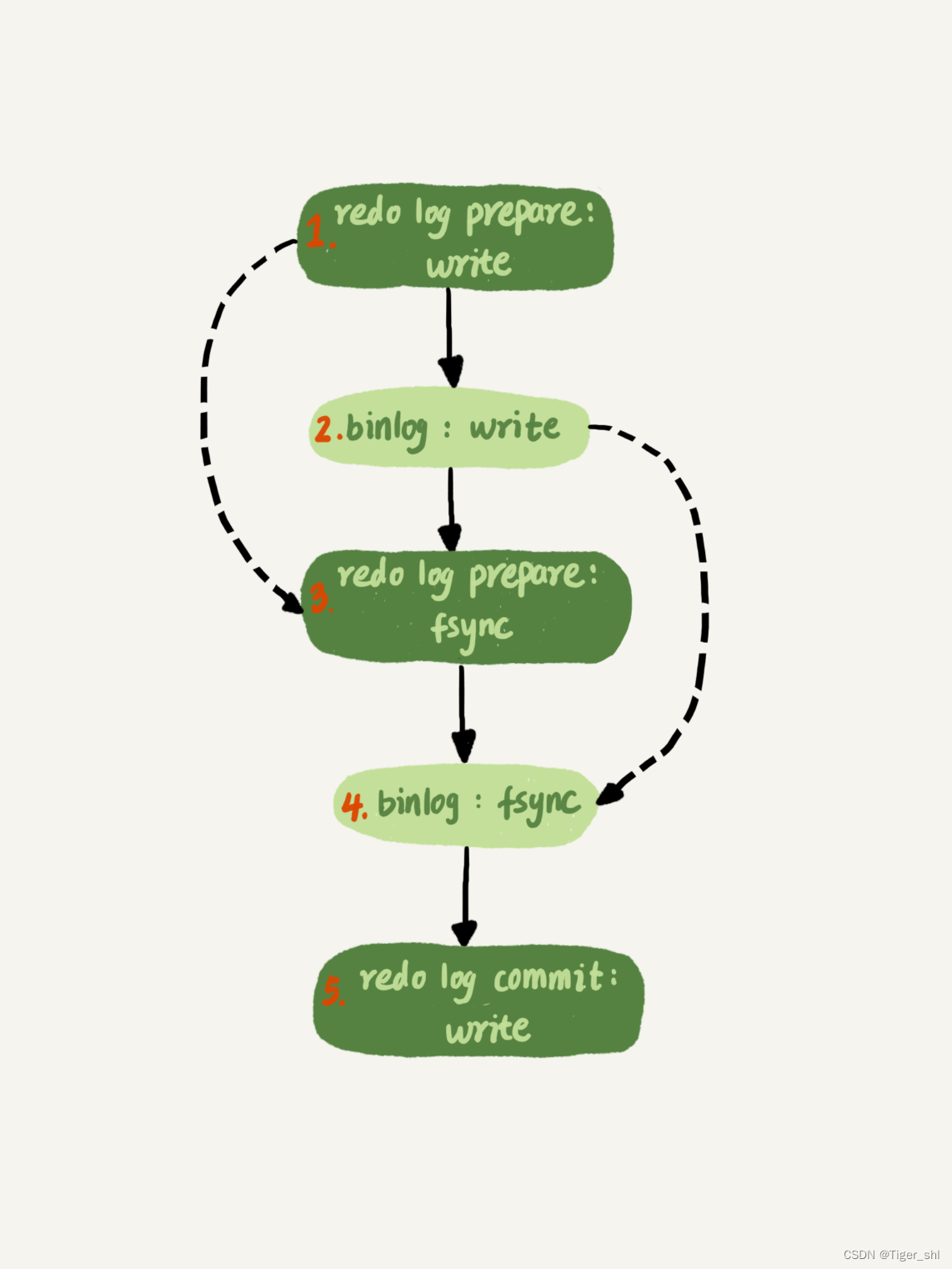
文章目录 1. MySql保证主备一致1.1 MySQL 主备的基本原理1.2 binlog 的三种格式对比1.3 循环复制问题 2. MySql保证高可用2.1 主备延迟2.2 主备延迟的来源2.3 可靠性优先策略2.4 可用性优先策略 3. 备库为何会延迟很久-备库并行复制能力3.1 MySQL 5.6 版本的并行复制策略3.2 Ma…...

Spring篇---第七篇
系列文章目录 文章目录 系列文章目录一、说说事务的传播级别二、Spring 事务实现方式三、Spring框架的事务管理有哪些优点一、说说事务的传播级别 Spring事务定义了7种传播机制: PROPAGATION_REQUIRED:默认的Spring事物传播级别,若当前存在事务,则加入该事务,若 不存在事务…...
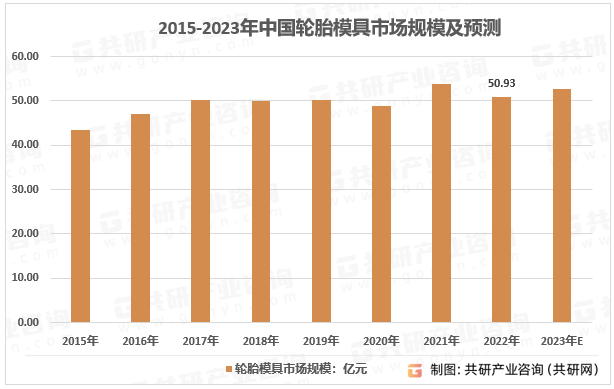
2023年中国轮胎模具需求量、竞争格局及行业市场规模分析[图]
轮胎模具是轮胎生产线中的硫化成形装备,是高技术含量、高精度及高附加值的个性化模具产品,尤其是轮胎的花纹、图案、字体以及其他外观特征的成形都依赖于轮胎模具,因此其制造技术难度较高。其主要功能是通过所成型材料(主要是橡塑…...
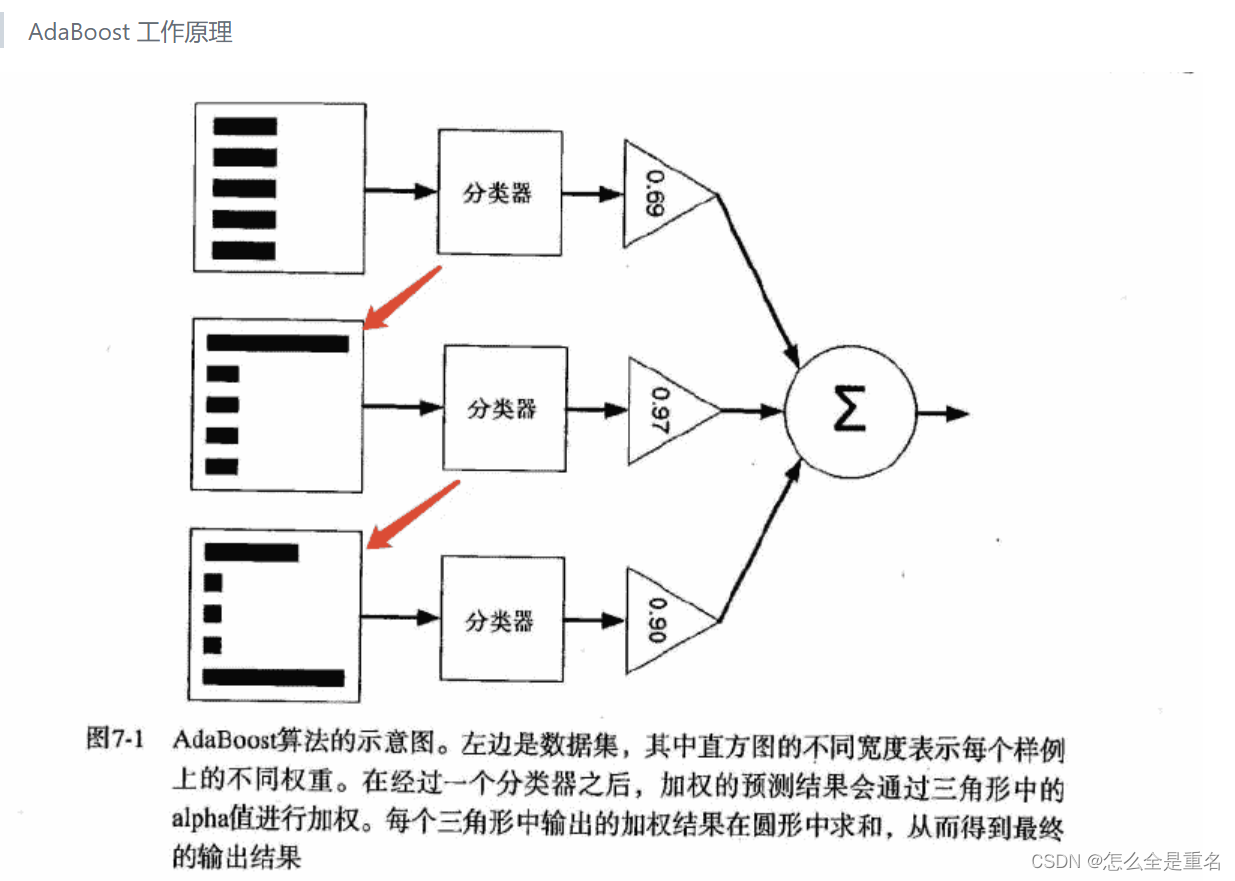
集成学习方法(随机森林和AdaBoost)
释义 集成学习很好的避免了单一学习模型带来的过拟合问题 根据个体学习器的生成方式,目前的集成学习方法大致可分为两大类: Bagging(个体学习器间不存在强依赖关系、可同时生成的并行化方法) 流行版本:随机森林(random forest)Boosting(个体…...

PeopleCode中Date函数的用法
语法 Date(date_num) 描述 The Date function takes a number in the form YYYYMMDD and returns a corresponding Date value. If the date is invalid, Date displays an error message. Date函数输入是一个形如“YYYYMMDD”的数字,返回一个相应的Date类型的值…...

解决 el-tree setChecked 方法偶尔失效的方法
目前在大多数公司中,菜单的权限控制都是不可或缺的功能 在和后端配合做权限控制的时候不可避免的会用到 el-tree 然而这个组件本身带的坑不少 我们需要回显对应角色拥有的菜单,在不严格的模式下,父节点的选中会连带子节点的选中 如果 &a…...
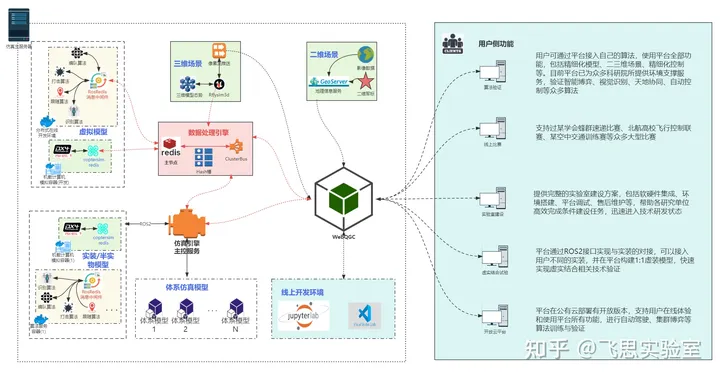
重磅发布!RflySim Cloud 智能算法云仿真平台亮相,助力大规模集群算法高效训练
RflySim Cloud智能算法云仿真平台(以下简称RflySim Cloud平台)是由卓翼智能及飞思实验室为无人平台集群算法验证、大规模博弈对抗仿真、人工智能模型训练等前沿研究领域研发的平台。主要由环境仿真模块、物理效应计算模块、多智能体仿真模块、分布式网络…...
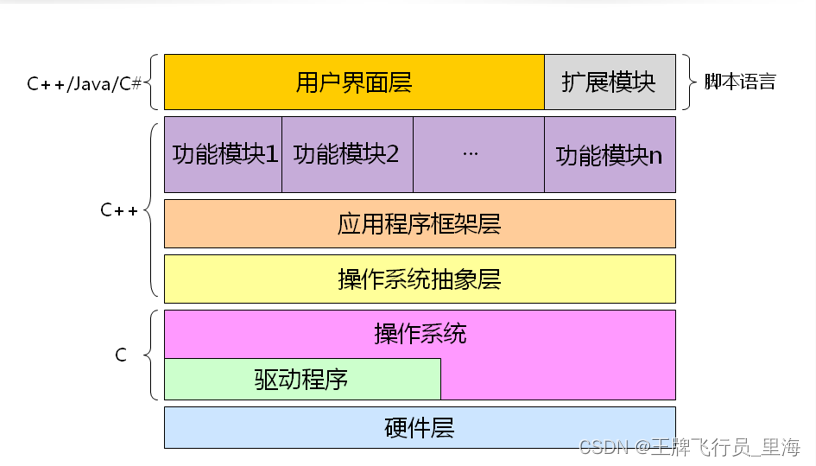
C++ 01.学习C++的意义-狄泰软件学院
一些历史 UNIX操作系统诞生之初是用汇编语言编写的随着UNIX系统的发展,汇编语言的开发效率成为瓶颈,所以需要一个新的语言替代汇编语言1971年通过对B语言改良,使其能直接产生机器代码,C语言诞生UNIX使用C语言重写,同时…...

微软正式发布开源应用平台 Radius平台
“ 10 月 18 日,微软 Azure 孵化团队正式发布开源应用平台 Radius,该平台将应用程序置于每个开发阶段的中心,重新定义应用程序的构建、管理与理解方式。” 简单的概括就是,它和Kubernetes不一样,Radius将应用程序放在每…...
)
排序算法(python)
排序算法 冒泡排序 一次比较相邻的两个数,每轮之后末尾的数字是确定的。 时间复杂度为 O ( n 2 ) O(n^2) O(n2),空间复杂度为 O ( 1 ) O(1) O(1),稳定。 def BUB(nums):for i in range(len(nums)):count 0for j in range(len(nums)-i-1)…...
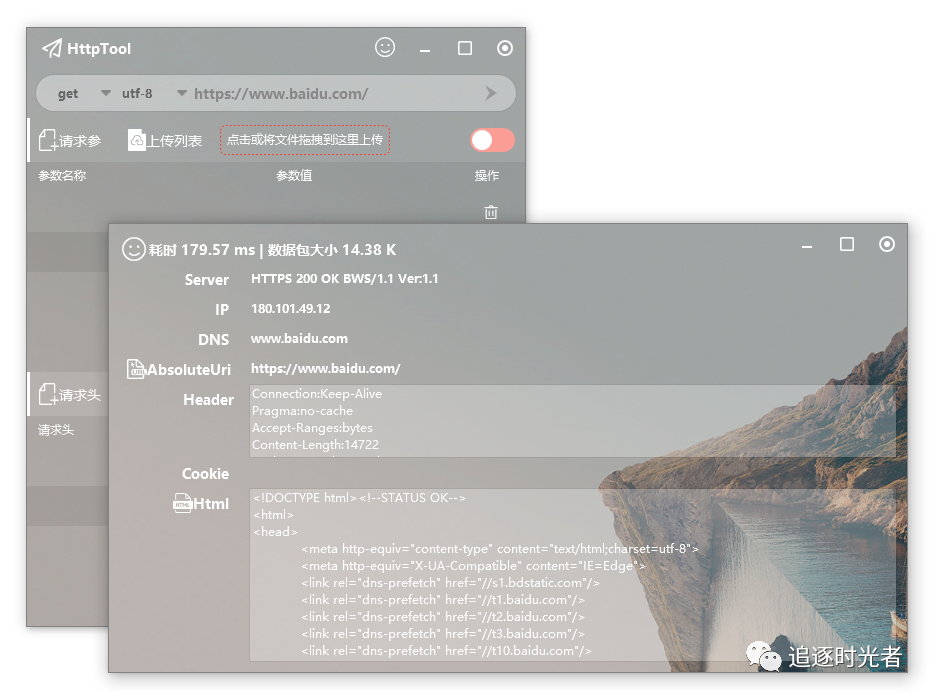
一款简单漂亮的WPF UI - AduSkin
前言 经常会有同学会问,有没有好看简单的WPF UI库推荐的。今天就给大家推荐一款简单漂亮的WPF UI,融合多个开源框架组件:AduSkin。 WPF是什么? WPF 是一个强大的桌面应用程序框架,用于构建具有丰富用户界面的 Windo…...
)
Java面试题-Java核心基础-第七天(String)
目录 一、String、StringBuffer、StringBuilder的区别 二、String为什么是不可变的 三、字符串拼接用""还是用StringBuilder 四、String 中的equals和Object中的equals的区别 五、字符串常量池的作用了解吗? 六、String s1 new String("abc&qu…...

路飞项目多方式登录、手机号短信验证注册接口
登录注册页面分析 用户板块需要写的接口 用户名密码登录(多方式登录)获取手机验证码接口手机号验证码登录注册接口验证手机号是否存在接口 验证手机号是否存在 视图类 from rest_framework.viewsets import ViewSet from rest_framework.decorator…...

信息学奥赛一本通-编程启蒙3003:练2.1 春节快乐
3003:练2.1 春节快乐 时间限制: 1000 ms 内存限制: 65536 KB 提交数: 10805 通过数: 7830 【题目描述】 一年一度的春节到啦!试着把你的春节祝福表达在代码中吧。 【输入】 无 【输出】 输出一行"Happy Spring Festival!" 【输入…...
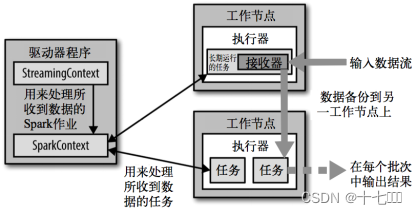
SparkStreaming入门
概述 实时/离线 实时:Spark是每个3秒或者5秒更新一下处理后的数据,这个是按照时间切分的伪实时。真正的实时是根据事件触发的数据计算,处理精度达到ms级别。离线:数据是落盘后再处理,一般处理的数据是昨天的数据&…...
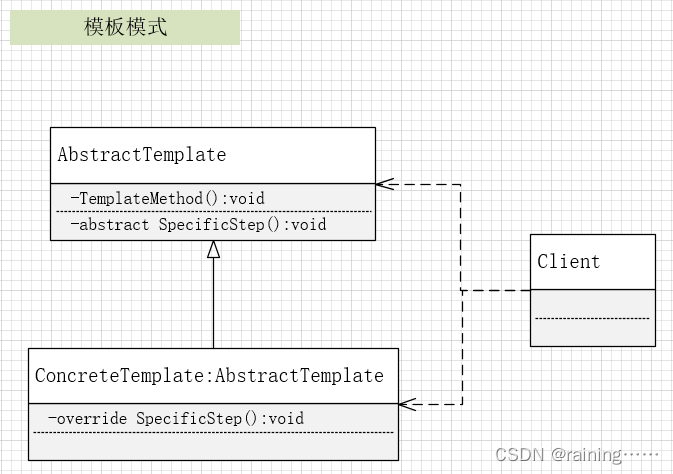
设计模式:模板模式(C#、JAVA、JavaScript、C++、Python、Go、PHP)
简介: 模板模式,它是一种行为型设计模式,它定义了一个操作中的算法的框架,将一些步骤延迟到子类中实现,使得子类可以不改变一个算法的结构即可重定义该算法的某些特定步骤。 通俗地说,模板模式就是将某一行…...
基于Java的图书商城管理系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding) 代码参考数据库参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者&am…...
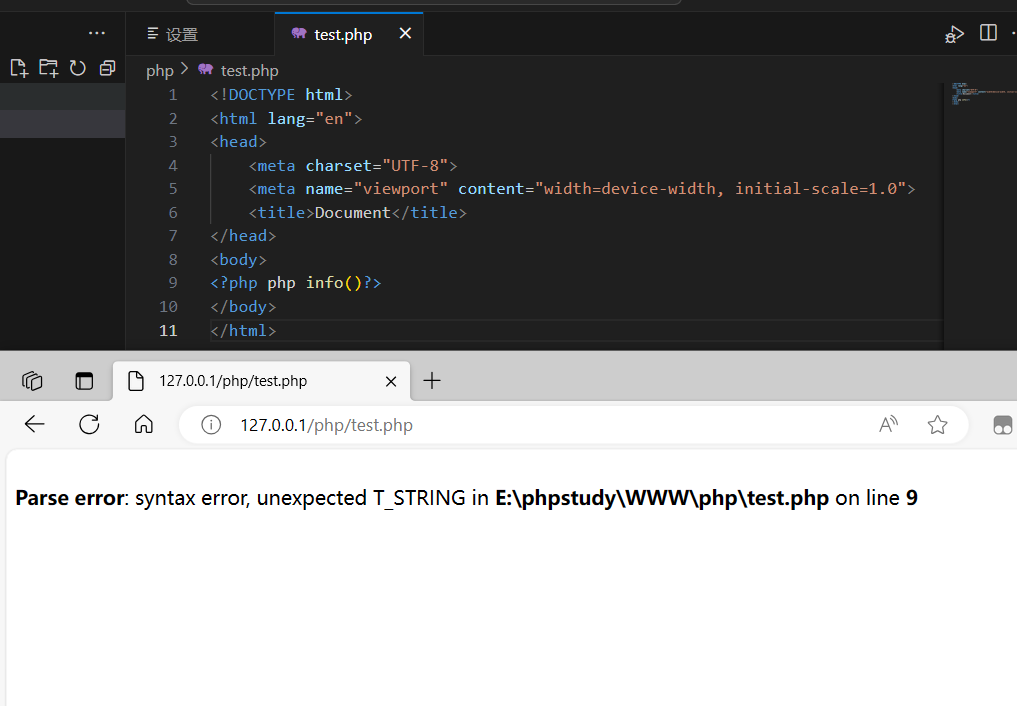
PHP 基础
PHP 基础 概述 在PHP 文件中,可以与HTML 和JavaScript 混编。 开始标记<?php 表示进入PHP 模式,结束标记?>,标识退出PHP 模式。 PHP 模式之外的内容会被作为字符输出到浏览器中。 PHP 在服务端执行,HTML 和 JS 在浏览…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
