【算法题】2906. 构造乘积矩阵
题目:
给你一个下标从 0 开始、大小为 n * m 的二维整数矩阵 grid ,定义一个下标从 0 开始、大小为 n * m 的的二维矩阵 p。如果满足以下条件,则称 p 为 grid 的 乘积矩阵 :
对于每个元素 p[i][j] ,它的值等于除了 grid[i][j] 外所有元素的乘积。乘积对 12345 取余数。
返回 grid 的乘积矩阵。
示例 1:
输入:grid = [[1,2],[3,4]]
输出:[[24,12],[8,6]]
解释:p[0][0] = grid[0][1] * grid[1][0] * grid[1][1] = 2 * 3 * 4 = 24
p[0][1] = grid[0][0] * grid[1][0] * grid[1][1] = 1 * 3 * 4 = 12
p[1][0] = grid[0][0] * grid[0][1] * grid[1][1] = 1 * 2 * 4 = 8
p[1][1] = grid[0][0] * grid[0][1] * grid[1][0] = 1 * 2 * 3 = 6
所以答案是 [[24,12],[8,6]] 。
示例 2:
输入:grid = [[12345],[2],[1]]
输出:[[2],[0],[0]]
解释:p[0][0] = grid[0][1] * grid[0][2] = 2 * 1 = 2
p[0][1] = grid[0][0] * grid[0][2] = 12345 * 1 = 12345. 12345 % 12345 = 0 ,所以 p[0][1] = 0
p[0][2] = grid[0][0] * grid[0][1] = 12345 * 2 = 24690. 24690 % 12345 = 0 ,所以 p[0][2] = 0
所以答案是 [[2],[0],[0]] 。
提示:
1 <= n == grid.length <= 10^5
1 <= m == grid[i].length <= 10^5
2 <= n * m <= 10^5
1 <= grid[i][j] <= 10^9
java代码:
class Solution {public int[][] constructProductMatrix(int[][] grid) {final int MOD = 12345;int n = grid.length, m = grid[0].length;int[][] p = new int[n][m];long suf = 1; // 后缀乘积for (int i = n - 1; i >= 0; i--) {for (int j = m - 1; j >= 0; j--) {p[i][j] = (int) suf; // p[i][j] 先初始化成后缀乘积suf = suf * grid[i][j] % MOD;}}long pre = 1; // 前缀乘积for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {p[i][j] = (int) (p[i][j] * pre % MOD); // 然后再乘上前缀乘积pre = pre * grid[i][j] % MOD;}}return p;}
}
相关文章:

【算法题】2906. 构造乘积矩阵
题目: 给你一个下标从 0 开始、大小为 n * m 的二维整数矩阵 grid ,定义一个下标从 0 开始、大小为 n * m 的的二维矩阵 p。如果满足以下条件,则称 p 为 grid 的 乘积矩阵 : 对于每个元素 p[i][j] ,它的值等于除了 g…...
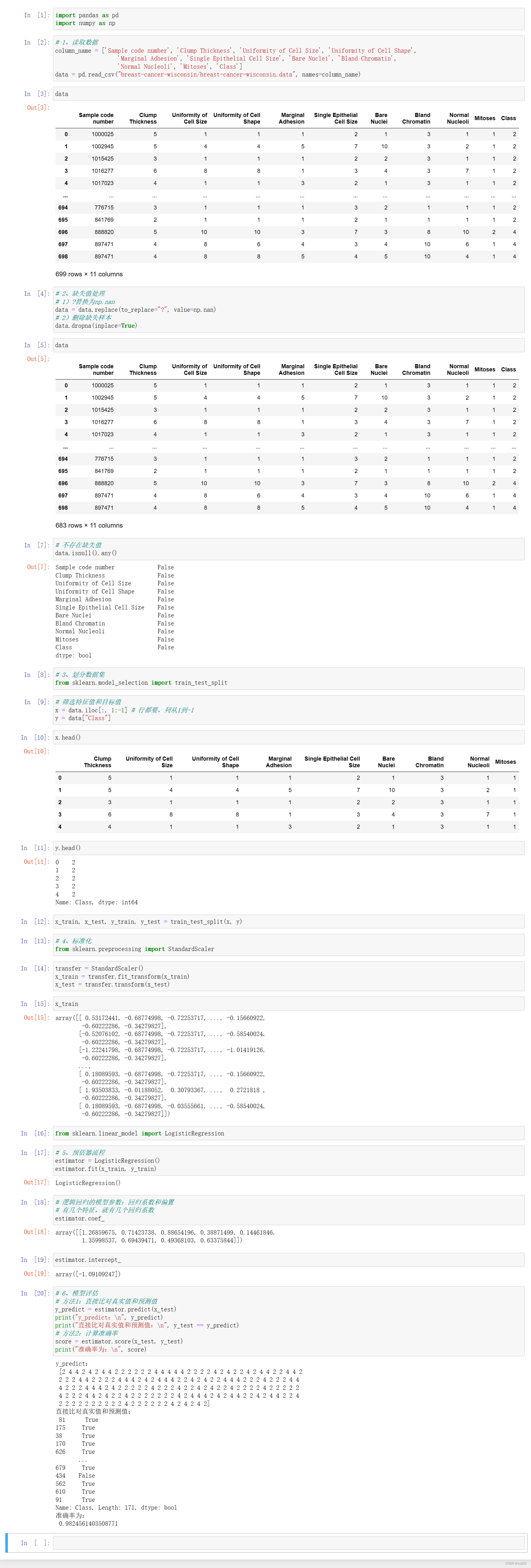
机器学习基础之《回归与聚类算法(4)—逻辑回归与二分类(分类算法)》
一、什么是逻辑回归 1、逻辑回归(Logistic Regression)是机器学习中的一种分类模型,逻辑回归是一种分类算法,虽然名字中带有回归,但是它与回归之间有一定的联系。由于算法的简单和高效,在实际中应用非常广…...
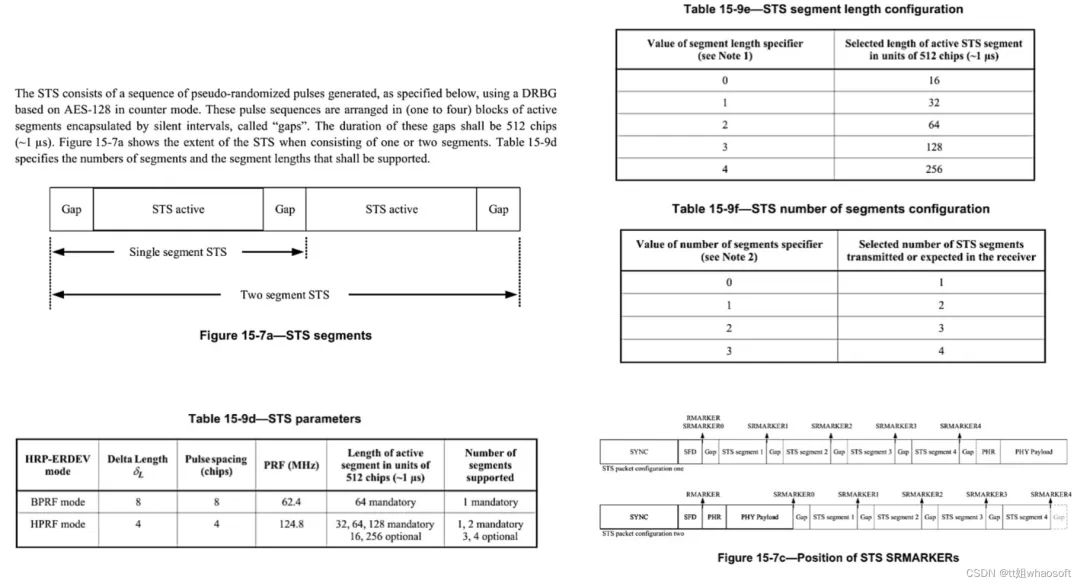
UWB安全数据通讯STS-加密、身份认证
DW3000系列才能支持UWB安全数据通讯,DW1000不支持 IEEE 802.15.4a没有数据通讯安全保护机制,IEEE 802.15.4z中指定的扩展得到增强(在PHY/RF级别):增添了一个重要特性“扰频时间戳序列(STS)”&a…...

vue3中去除eslint严格模式
vue3中去除eslint严格模式 1、全局搜索:extends 2、一般在package.json或者vue.config.js中,直接删除掉vue/standard,重启项目。(在package.json文件中,编译不允许有注释,所以直接删掉)...
Win10如何彻底关闭wsappx进程?
Win10如何彻底关闭wsappx进程?在Win10电脑中,用户看到了wsappx进程占用了大量的系统资源,所以想结束wsappx进程,提升电脑的运行速度。但是,用户们不知道彻底关闭掉wsappx进程的方法,那么接下来小编就给大家…...
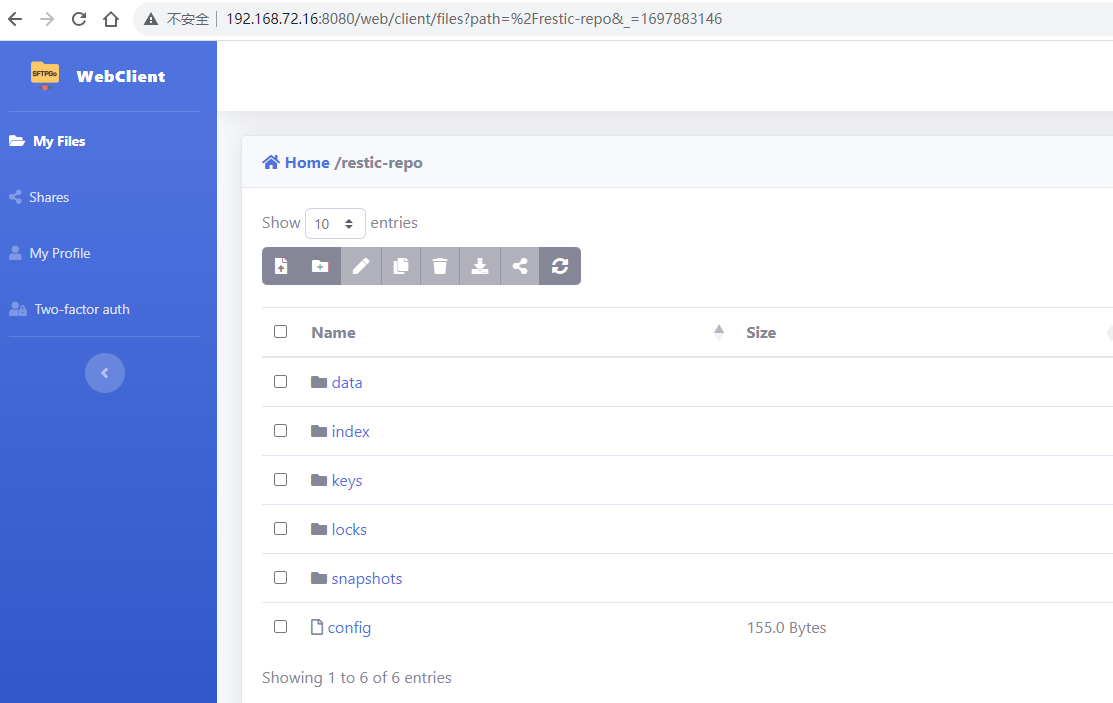
docker 安装 sftpgo
sftpgo 简介 sftpgo 是一个功能齐全且高度可配置的 SFTP 服务器,具有可选的 HTTP/S、FTP/S 和 WebDAV 支持。支持多种存储后端:本地文件系统、加密本地文件系统、S3(兼容)对象存储、Google 云存储、Azure Blob 存储、SFTP。 官…...
 创建一个场景)
threejs (一) 创建一个场景
引入 npm install three import * as THREE from three;const scene new THREE.Scene();或者使用bootCDN复制对应的版本连接 <script src"https://cdn.bootcdn.net/ajax/libs/three.js/0.156.1/three.js"></script>基础知识 场景、相机、渲染器 通过…...

二分查找,求方程多解
1.暴力遍历: 解为两位小数,故0.001的范围肯定可以包含(零点存在) 2.均分为区间长度为1的小区间(由于两解,距离不小于1),一个区间最多一个解 1.防止两边端点都为解 2&…...

代码随想录算法训练营第二十九天 | 回溯算法总结
代码随想录算法训练营第二十九天 | 回溯算法总结 1. 组合问题 1.1 组合问题 在77. 组合中,我们开始用回溯法解决第一道题目:组合问题。 回溯算法跟k层for循环同样是暴力解法,为什么用回溯呢?回溯法的魅力,用递…...
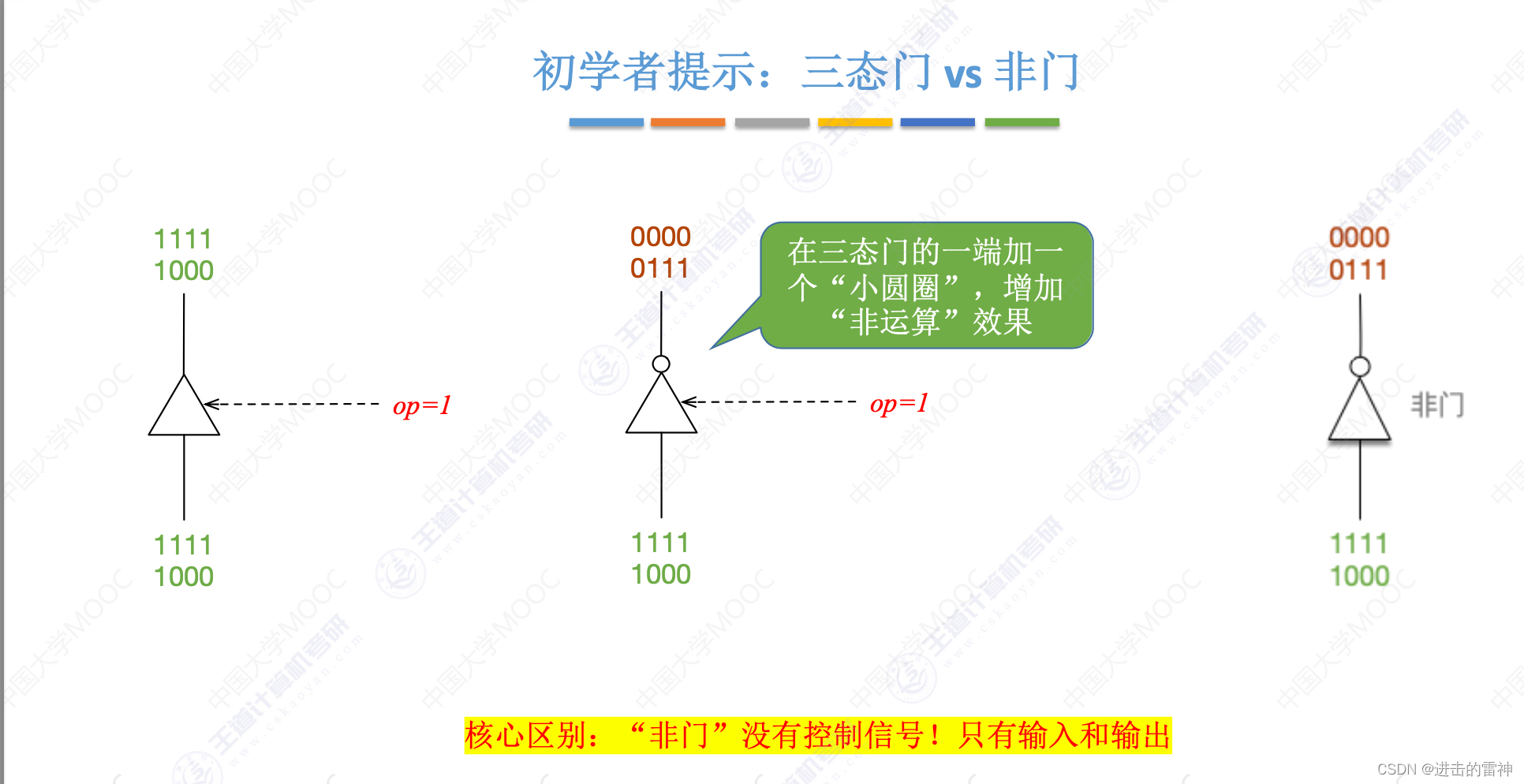
运算方法和运算电路
一、逻辑门电路 1、逻辑门电路基础总结 2、异或运算妙用 3、逻辑常用公式 二、加法器(重点) 1、标志位的生成原理 2、加法器总结 三、多路门选择器,三态门...
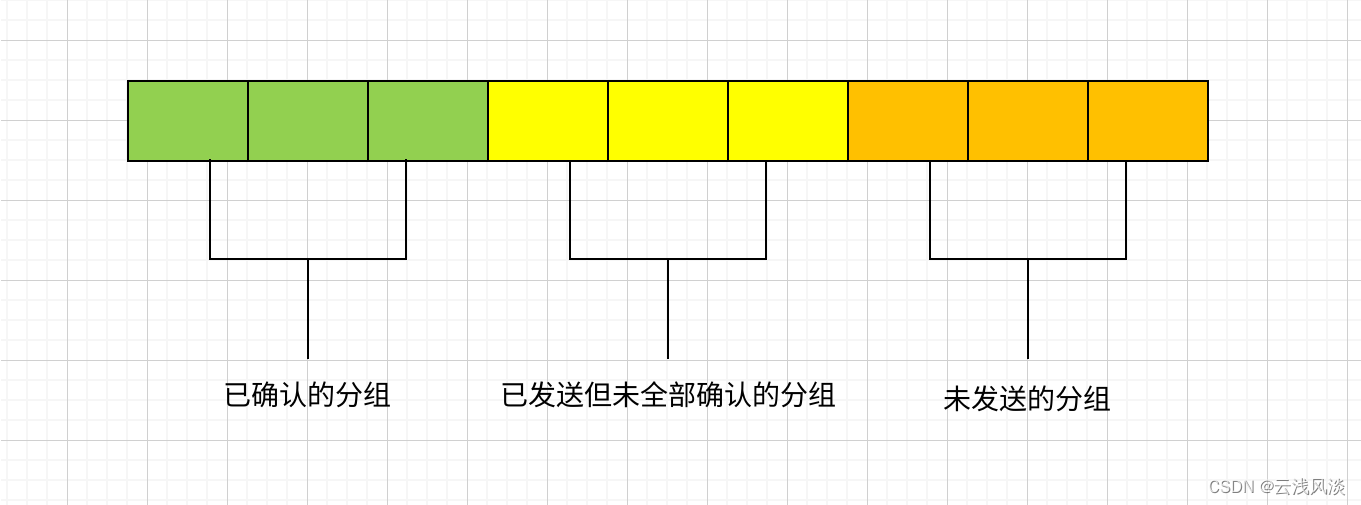
计算机网络篇之TCP滑动窗口
文章目录 前言概述 前言 在网络数据传输时,若传输的原始数据包比较大,会将数据包分解成多个数据包进行发送。需要对数据包确认后,才能发送下一个数据包。在等待确认包的这个过程浪费了大量的时间,不过还好TCP引入了滑动窗口的概念…...

本地安装telepresence,访问K8S集群 Mac(m1) 非管理員
kubeconfig 一.安装telepresence 1.安装 Telepresence Quickstart | Telepresence (1)brew install datawire/blackbird/telepresence 2.配置 目录kubectl 将使用默认的 kubeconfig 文件:$HOME/.kube/config 创建文件夹&…...
 — 训练机器学习模型用GPU还是NUP更有优势(基于文心一言的回答))
今日思考(2) — 训练机器学习模型用GPU还是NUP更有优势(基于文心一言的回答)
前言 深度学习用GPU,强化学习用NPU。 1.训练深度学习模型,强化学习模型用NPU还是GPU更有优势 在训练深度学习模型时,GPU相比NPU有优势。GPU拥有更高的访存速度和更高的浮点运算能力,因此更适合深度学习中的大量训练数据、大量矩阵…...

8.3 C++ 定义并使用类
C/C语言是一种通用的编程语言,具有高效、灵活和可移植等特点。C语言主要用于系统编程,如操作系统、编译器、数据库等;C语言是C语言的扩展,增加了面向对象编程的特性,适用于大型软件系统、图形用户界面、嵌入式系统等。…...

Git学习笔记——超详细
Git笔记 安装git: apt install git 创建版本库: git init 添加文件到版本库: git add 文件 提交文件到仓库: git commit -m “注释” 查看仓库当前的状态信息: git status 查看修改内容和之前版本的区别&am…...
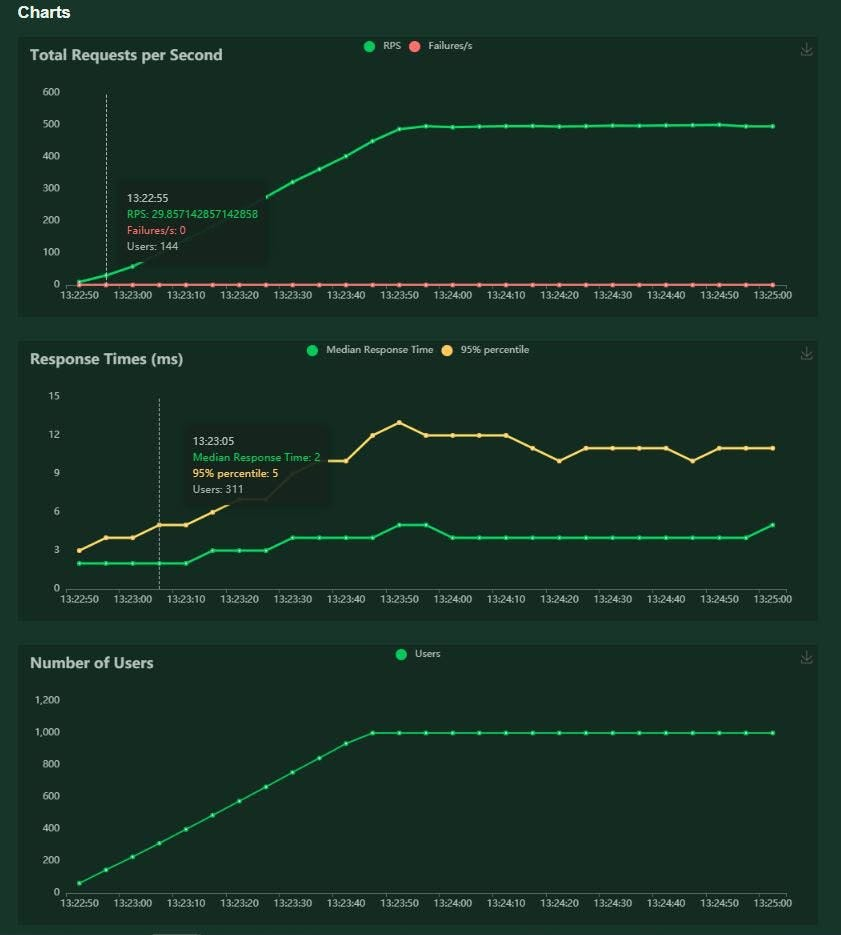
Locust负载测试工具实操
本中介绍如何使用Locust为开发的服务/网站执行负载测试。 Locust 是一个开源负载测试工具,可以通过 Python 代码构造来定义用户行为,避免混乱的 UI 和臃肿的 XML 配置。 步骤 设置Locust。 在简单的 HTTP 服务上模拟基本负载测试。 准备条件 Python…...
关闭mysql,关闭redis服务
1. 关闭redis服务: 查询redis安装目录: whereis redis which redis find / -name redis 关闭redis服务: redis-cli -h 127.0.0.1 -p 6379 auth 输入密码 shutdown 关闭redis服务 2. 关闭mysql服务: 查询mysql安装目录&…...

微机原理:汇编语言语句类型与格式
文章目录 壹、语句类型1、语句分类2、常用伪代码和运算符2.1数据定义伪指令2.1.1字节定义伪指令DB(8位)2.1.2字定义伪指令DW(16位)2.1.3双字节伪指令DD2.1.4 多字节定义DF/DQ/DT(了解) 2.2 常用运算符2.2.1…...

iOS Flutter Engine源码调试和修改
iOS Flutter Engine源码调试和修改 1. 前提:2. 步骤:3. 参考资料 1. 前提: 已将成功安装deop_tools工具已经通过gclient命令同步好flutter engine源码 2. 步骤: 进入engine/src目录 创建flutter engine构建文件 真机文件debug模式: ./flu…...
Java日志系统之Log4j
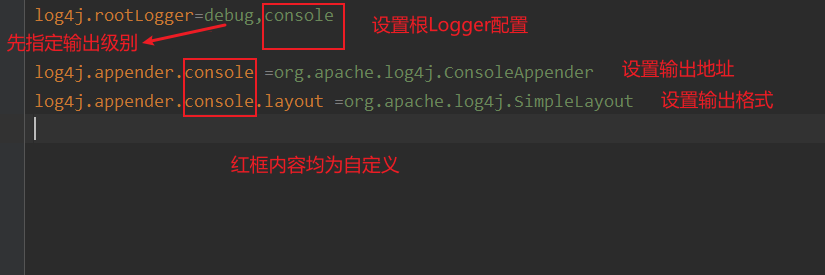
目录 Log4J Log4j的简单使用 日志级别 Log4j的组件 Loggers Appenders Layout Layout格式 设置配置文件加载 配置文件解析 Log4J 是Apache下开源的日志框架 Log4j的简单使用 Testpublic void testLog4J(){Logger logger Logger.getLogger(Log4jTest.class);logger…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...
