牛客小白月赛79
给定一个数字n,你可以对它进行接下来的操作——
- 选择数字中任意一个数位删除
例如对1024选择操作百位,数字则变成了124;对1024选择操作千位,数字则变成了024
我们称一个数字是干净的,当且仅当数字满足以下任意一种情况:
- 这个数字是偶数且不含前导零
- 这个数字为空
请问最少需要进行多少次操作,使得数字nnn变成干净的
输入描述:
第一行包含一个整数 (1≤n≤10^9),表示这个数字的大小
输入的数字保证不含前导零输出描述:
输出最少需要的操作次数。
注意,因为一定能使得数字删成空,所以当前数字一定能变成干净的
示例1
输
1024输出
0说明
当前数字无需操作便满足条件
想复杂了,我就说别人做这么快。
直接判断最后一位的偶数就行。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fp(i,a,b) for(int i=a;i<=b;++i)
#define PII pair<int,int>
const int N=2e5+10;
const int mod=1e9+7;
const double eps=1e-5;
typedef double db;
string s;
signed main()
{
cin>>s;
int sz=s.size();
int pos=-1;
for(int i=sz-1;i>=0;i--)
{
int x=s[i]-'0';
if(x%2==0)
{
pos=i;
break;
}
}
if(pos==-1)
{
cout<<sz<<"\n";
}
else
{
int pos1=0;
int ans=0;
for(int i=0;i<=pos;i++)
{
int x=s[i]-'0';
if(x==0)
{
ans++;
}
else
{
break;
}
}
cout<<ans+sz-1-pos<<"\n";
}
return 0;
}
B、
有n个正整数,现在,你可以选择将其中一些数放进灵异背包中,使得背包里面所有数的总和为偶数且最大,求能得到的最大值是多少?
注意:如果你不将任何数放进灵异背包,此时背包总和为0输入描述:
第一行包含一个正整数 (1≤n≤10^5),表示数字的数量 接下来n行包含n个正整数 a1,a2...,an (1≤ai≤2×10^4),表示数字的大小输出描述:
输出一个整数,表示灵异背包所有数的总和为偶数且最大是多少示例1
输入
3 2 5 6输出
8说明
当灵异背包里面有(2,5,6),此时总和为2+5+6=13,为奇数,不满足条件 当灵异背包里面有(2,6),此时总和为2+6=8,为偶数,且为最大值示例2
输入
1 3输出
0说明
选择的灵异背包为空,总和为0
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fp(i,a,b) for(int i=a;i<=b;++i)
#define PII pair<int,int>
const int N=2e5+10;
const int mod=1e9+7;
const double eps=1e-5;
typedef double db;
string s;
int n;
int a[N];
int b[N],cnt;
signed main()
{cin>>n;int sum=0;fp(i,1,n){cin>>a[i];if(a[i]&1){b[++cnt]=a[i];}else{sum+=a[i];}}if(cnt&1){sort(b+1,b+1+cnt);fp(i,2,cnt){sum+=b[i];}}else{fp(i,1,cnt){sum+=b[i];}}cout<<sum<<"\n";return 0;
} C、
给你一个长度为n的数列。求这个数列中连续区间的mex乘gcd的最大值是多少?
示例1
输入
5 0 1 2 1 4输出
3
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fp(i,a,b) for(int i=a;i<=b;++i)
#define PII pair<int,int>
const int N=2e5+10;
const int mod=1e9+7;
const double eps=1e-5;
typedef double db;
string s;
int n;
int a[N];
int b[N];
signed main()
{cin>>n;int cnt=0;for(int i=1;i<=n;i++){cin>>a[i];if(a[i]==0)cnt++;b[a[i]]++;}if(cnt==n){cout<<0<<"\n";return 0;}int mmax=0;for(int i=1;i<=n;i++){if(a[i]==0){mmax=max(mmax,a[i-1]);mmax=max(mmax,a[i+1]);}} for(int i=0;i<=n;i++){if(b[i]==0){mmax=max(mmax,i);break;}}cout<<mmax<<"\n";return 0;
} //这个区间是最少需要1个0
//如果这个区间有1 结果为区间的mex值
//如果这个区间没有1 结果为区间的gcd值 gcd(0,0)=0 qwq
D、
长途是ACM大陆一只快乐的小男孩。今天,他在cf战场上历练,遭遇了TTT波丧尸
长途快被丧尸咬死啦!幸好他手中的两把武器都还有20^{20^{20^{20}}}枚子弹,一枚子弹可以击中一个丧尸
- 武器1——【AC】:每次射击可以发射一枚子弹
- 武器2——【AK-47】:每次射击可以同时朝当前每个丧尸均发射一枚子弹
然而,丧尸有种特殊的能力,每次击中并不会死掉,反而会立刻复制出一个新的丧尸
长途有点绝望。幸好他发现当前这波的所有丧尸都处在一个特殊的圆盘上!这个圆盘被称为圆神,当丧尸的数量是2202^{20}220的倍数时,可以选择启动这个装置,消灭当前这波的全部丧尸!!!
值得注意的是,一共有TTT大波丧尸,只有当一波的丧尸被全部消灭后,下一波的丧尸才会出现,并且手中武器的子弹数也会恢复
情况很紧急,长途请你帮帮他。对于每一波丧尸,最少需要射击多少次才能消灭这一波的所有丧尸。若消耗完所有的子弹都无法消灭这一波的所有丧尸,请输出−1-1−1输入描述:
第一行包含一个整数TTT,表示长途遭遇了 T (1≤T≤10^5) 波丧尸 对于每波丧尸: 仅输入一行,包含一个正整数 (1≤n≤10^9),表示当前这波的丧尸数输出描述:
对于每波丧尸: 仅输出一行,若消耗完所有的子弹都无法消灭这一波的所有丧尸,输出−1;否则输出消灭当前这波的所有丧尸所需要的最少射击次数示例1
输入
3 1048575 1048576 1输出
1 0 20
我不理解我写的为什么错了
错误代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fp(i,a,b) for(int i=a;i<=b;++i)
#define PII pair<int,int>
const int N=2e5+10;
const int mod=1e9+7;
const double eps=1e-5;
typedef double db;
string s;
int x=1048576;
int a[N];
void solve()
{int n;cin>>n;if(n%x==0){cout<<0<<"\n";return;}int mmin=20;for(int i=n;i<=n+20;i++){int cnt=20;int x=i;while(x%2==0){x/=2;cnt--;}mmin=min(mmin,cnt+i-n);}cout<<mmin<<"\n";
}
signed main()
{int T;cin>>T;while(T--){solve();}return 0;
} //这个区间是最少需要1个0
//如果这个区间有1 结果为区间的mex值
//如果这个区间没有1 结果为区间的gcd值 正确代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fp(i,a,b) for(int i=a;i<=b;++i)
#define PII pair<int,int>
const int N=2e5+10;
const int mod=1e9+7;
const double eps=1e-5;
typedef double db;
string s;
int x=1048576;
int a[N];
void solve()
{int n;cin>>n;if(n%x==0){cout<<0<<"\n";return;}int mmin=20;n%=x; for(int i=n;i<=n+20;i++){int cnt=20;int x=i;while(x%2==0){x/=2;cnt--;}mmin=min(mmin,cnt+i-n);}cout<<mmin<<"\n";
}
signed main()
{int T;cin>>T;while(T--){solve();}return 0;
} //这个区间是最少需要1个0
//如果这个区间有1 结果为区间的mex值
//如果这个区间没有1 结果为区间的gcd值 我后来用的代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fp(i,a,b) for(int i=a;i<=b;++i)
#define PII pair<int,int>
const int N=2e5+10;
const int mod=1e9+7;
const double eps=1e-5;
typedef double db;
string s;
int x=1048576;
int a[N];
void solve()
{int n;cin>>n;if(n%x==0){cout<<0<<"\n";return;}int mmin=20;for(int i=0;i<=20;i++){int g=0;int N=n+i;while(N%x!=0)N<<=1,g++;mmin=min(mmin,i+g);}cout<<mmin<<"\n";
}
signed main()
{int T;cin>>T;while(T--){solve();}return 0;
} //这个区间是最少需要1个0
//如果这个区间有1 结果为区间的mex值
//如果这个区间没有1 结果为区间的gcd值 E、
丧尸涌入ACM大陆,幸好宁小夏同学在厕所里面研制出了时光机回到过去,给ACM大陆的封印之门设置了密码锁
- 这个密码锁很特别,密码锁上只有六个按钮,分别是"@" "q" "." "c" "o" "m"(不包含引号)
- 密码长度是给定的,当输入的密码后缀(即密码的最后七位)是"@qq.com"时才会被解锁
- 若输入的密码错误,将需要重新输入密码
例如:我们给定密码的长度是11,如果丧尸有一次输入的密码是"com@qq.comc",则密码错误;如果丧尸有一次输入的密码是"comc@qq.com",则密码正确。即当输入的密码满足"****@qq.com"的格式我们才认为密码是正确的
幸好丧尸十分的笨拙,每一秒钟会等概率随机按下一个按钮,当输入密码错误,需要重新输入密码,它会继续一直按下去,周而复始……直至输入正确
留给ACMer的时间不多了!现在已知密码的长度,大家都想知道丧尸破解密码的期望时间是多少(注:期望时间四舍五入取整数部分)
长途同学经过周密的计算,终于得到了四舍五入后丧尸破解密码的期望时间!同时他使用了mmm个在cf战场上获得的道具——【be-jiangly】,这个道具能够使得当前丧尸破解密码的期望时间变成平方。也就是说,设当前丧尸破解密码的期望时间为xxx,使用单个道具后期望时间变为了x^2
他激动地拿着最终丧尸破解密码的期望时间的草稿纸去找教练,结果被刚从厕所出来的宁小夏同学一不小心弄脏了草稿纸上的第一个数字(个位),/(ㄒoㄒ)/~~记性不好的长途已经忘记了被弄脏的数字是什么了,你能帮帮他吗?
问:被弄脏的个位数字是什么,如果丧尸破解密码的时间趋于正无穷,请输出−1
输入描述:
输入两个整数 n (1≤n≤10^9), (0≤m≤10^9),分别表示密码的长度和使用道具的数量输出描述:
若丧尸破解密码的时间趋于正无穷,请输出−1;否则请输出被弄脏的数字是什么示例1
输入
7 1输出
4说明
可怜巴巴的长途已经忘记怎么算出来的结果了,所以没有样例解释……
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fp(i,a,b) for(int i=a;i<=b;++i)
#define PII pair<int,int>
const int N=2e5+10;
const int mod=1e9+7;
const double eps=1e-5;
typedef double db;
string s;
int x=1048576;
int n,m;
void solve()
{cin>>n>>m;if(n<7){cout<<-1<<"\n";return;}int ans=279936;ans*=n;ans%=10;m=min(m,2ll);while(m--){ans=ans*ans%10;}cout<<ans<<"\n";return;
}
signed main()
{solve();return 0;
} //这个区间是最少需要1个0
//如果这个区间有1 结果为区间的mex值
//如果这个区间没有1 结果为区间的gcd值 如果完成一件事情的概率是 1/7,那么完成该事情的期望时间可以通过期望的概念计算得出。
几何分布描述了进行一系列独立试验,直到成功为止所需的试验次数。对于成功概率为 1/7 的几何分布,其期望值可以通过公式 E(X) = 1/p 来计算,其中 X 是完成该事情所需的时间,p 是完成该事情的概率。
因此,完成一件事情的期望时间为 E(X) = 1 / (1/7) = 7。
所以,完成一件事情的期望时间是 7。
可以类推到本题。
相关文章:

牛客小白月赛79
给定一个数字n,你可以对它进行接下来的操作—— 选择数字中任意一个数位删除 例如对1024选择操作百位,数字则变成了124;对1024选择操作千位,数字则变成了024 我们称一个数字是干净的,当且仅当数字满足以下任意一种…...
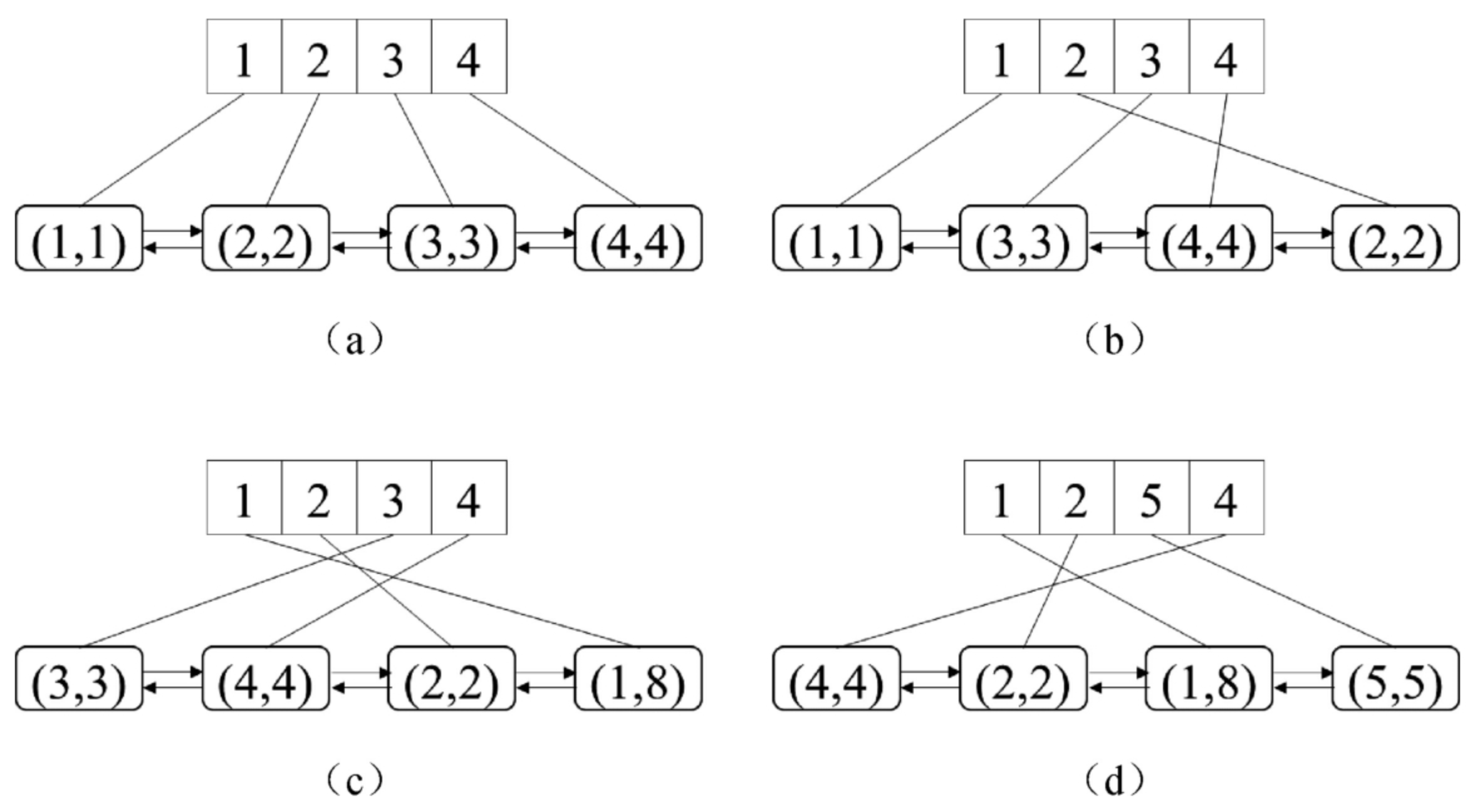
面试算法31:最近最少使用缓存
题目 请设计实现一个最近最少使用(Least Recently Used,LRU)缓存,要求如下两个操作的时间复杂度都是O(1)。 get(key):如果缓存中存在键key,则返回它对应的值…...

如何处理前端SEO(搜索引擎优化)?
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...
Leetcode—2529.正整数和负整数的最大计数【简单】
2023每日刷题(四) Leetcode—2529.正整数和负整数的最大计数 遍历法实现代码 int maximumCount(int* nums, int numsSize){int i;int neg 0, pos 0;for(i 0; i < numsSize; i) {if(nums[i] < 0) {neg;}if(nums[i] > 0) {pos;}}return (neg…...

数据结构-- 并查集
0. 引入 并查集是来解决等价问题的数据结构。 离散数学中的二元关系。 等价关系需满足自反性、对称性、传递性。 a ∈ S , a R a a R b & b R a a R b ∩ b R c > a R c a \in S, aRa \\ aRb \& bRa \\ aRb \cap bRc >aRc a∈S,aRaaRb&bRaaRb∩bRc>a…...
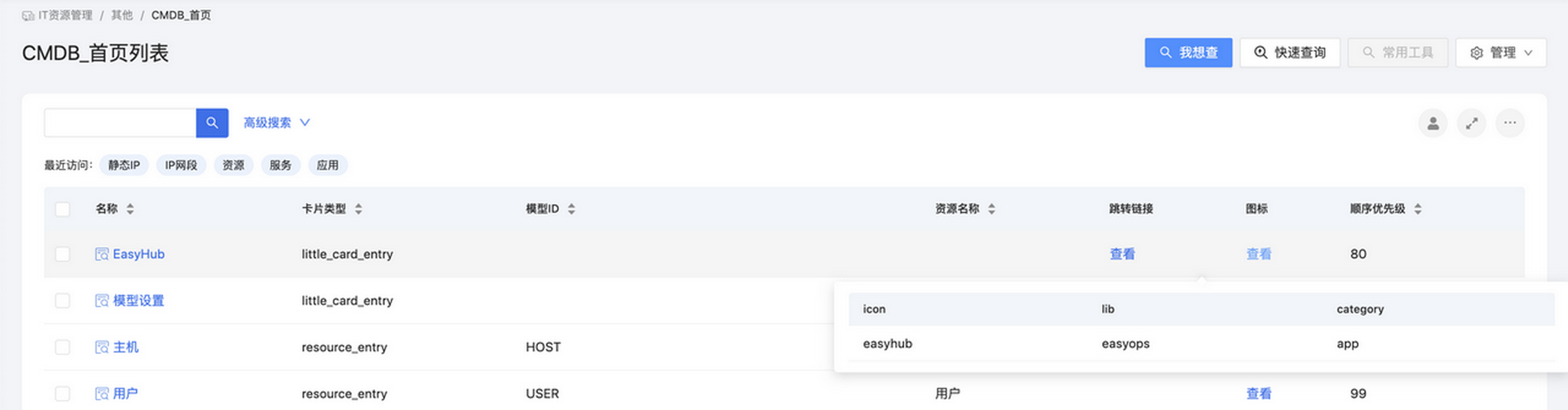
优维产品最佳实践第12期:IT资源管理首页丰富
背 景 当我们进入平台后,默认跳转至IT资源管理首页,因此该页面的优化与丰富将极大的提高平台使用者的体验和效率。优化后的首页可以更好地展示常用模型、小产品、外部系统、以及保存的所有关系查询和快速查询条件,使用户能够更快捷、方便…...
【Nginx34】Nginx学习:安全链接、范围分片以及请求分流模块
Nginx学习:安全链接、范围分片以及请求分流模块 又迎来新的模块了,今天的内容不多,但我们都进行了详细的测试,所以可能看起来会多一点哦。这三个模块之前也从来都没用过,但是通过学习之后发现,貌似还都挺有…...

PO模式在selenium自动化测试框架的优势
大家都知道po模式可以提高代码的可读性和减少了代码的重复,但是相对的缺点还有,今天通过本文一起学习下PO模式在selenium自动化测试框架的优势,需要的朋友可以参考下 PO模式简介 1.什么是PO模式 PO模型是:Page Object Model的简写 页面对象…...
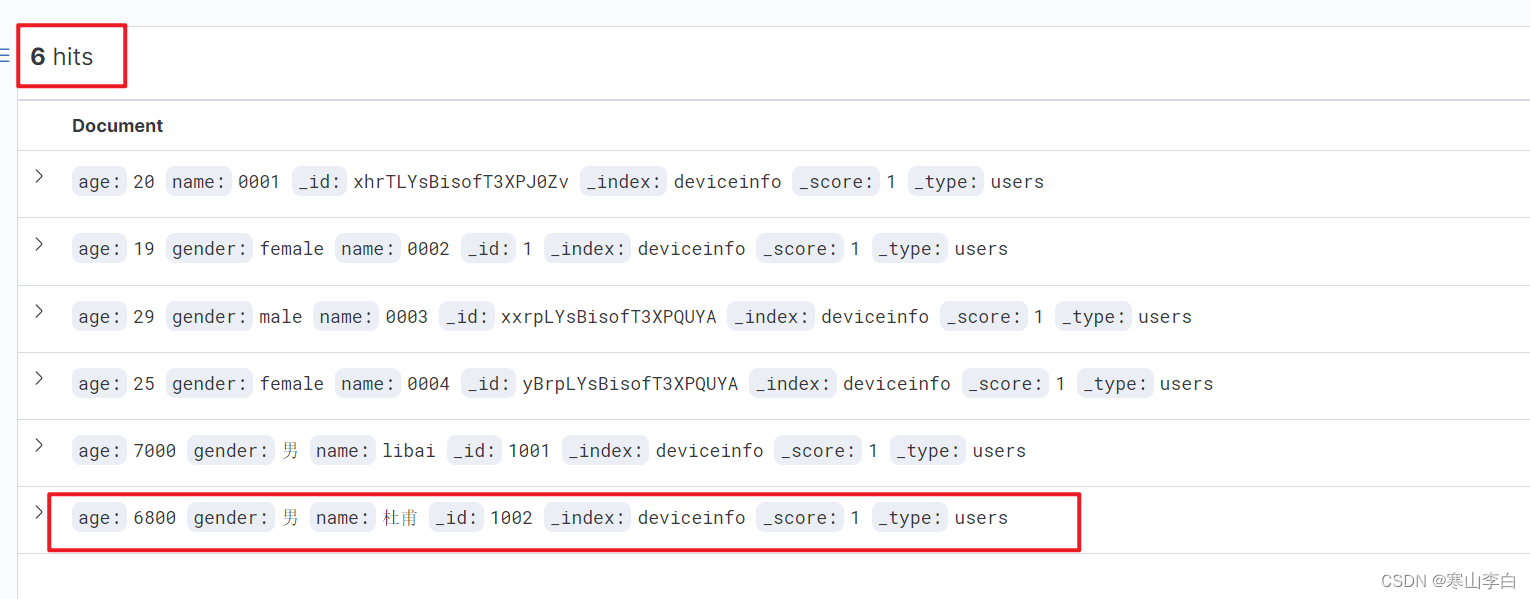
Java操作Elasticsearch(新增数据)
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

Android中级——MVVM
MVVM MVVM是什么?MVVM实现前提ModelViewModelView MVVM是什么? Model-View-ViewMode架构,可看作MVP改进版,将此前Presenter的逻辑操作交给ViewMode中的Binder去处理 Mode:封装数据存储及相关操作逻辑,与MV…...

AIGC:引领人工智能和游戏产业融合的里程碑
目录 引言: 一、AIGC简介 二、AIGC的意义和作用 三、AIGC的未来展望 四、AIGC的影响和成果 五、结论 引言: 人工智能技术的快速发展在过去几年中引起了全球范围内的广泛关注和热议。其中,AIGC(Artificial Intelligence and G…...
ubuntu安装rust教程
参考【Rust】Linux上安装Rust开发环境 sudo apt-get install curl# 注意,不开代理很可能下不到,一直报403 export RUSTUP_DIST_SERVERhttps://mirrors.ustc.edu.cn/rust-static export RUSTUP_UPDATE_ROOThttps://mirrors.ustc.edu.cn/rust-static/rustu…...

iOS UIWebView与WKWebView 那些事
一、前言介绍 UIWebView 是 iOS 2 中推出的网页容器,UIWebView是最占内存的控件;直到 iOS 8 以后,苹果推出了 WebKit 框架,其中 WKWebView 正式被推出来接替 UIWebView 的位置;iOS 12 中,苹果正式弃用 UIWebView,要求开发者用 WKWebView 全面替换 UIWebView,apple 官方…...
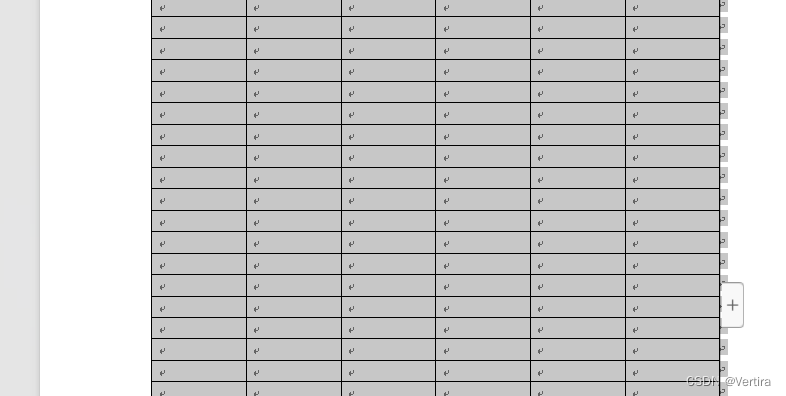
wps/word 之 word中的两个表格 如何合并成为一个表格(已解决)
第一步:新建两个表格: 如何实现上面的两个表格合并呢? 分别选定每个表格,然后鼠标右键---》表格属性 在表格属性中的 表格---》选择 无文字环绕。 第二个表格按照同样的方法 设置 无文字环绕。 然后将中的文本行删去即可以了。选…...
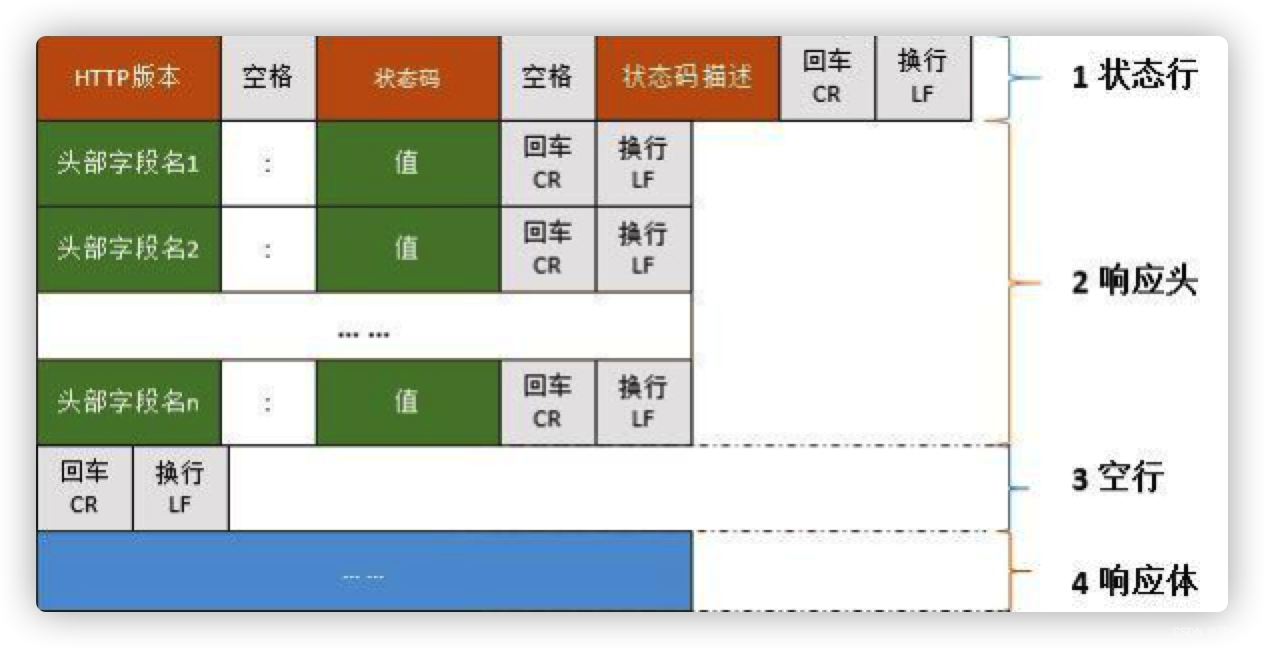
02HTML功能元素
1.功能元素 1.1.列表标签 列表标签的作用: 给一堆数据添加列表语义, 也就是告诉搜索引擎告诉浏览器这一堆数据是一个整体 - HTML中列表标签的分类 无序列表(最多)(unordered list) 有序列表(最少)(ordered list) 定义列表(其次)(definition list) 1.1.1.无序列…...

并发编程-延时队列DelayQueue
数据结构学习网站: Data Structure Visualization 思维导图 DelayQueue (延时队列) DelayQueue 是一个支持延时获取元素的阻塞队列 , 内部采用优先队列 PriorityQueue 存储元素,同时元素必须实现 Delayed 接口&#x…...

Python之哈希表-遍历和有序性
Python之哈希表-遍历和有序性 有序性 字典元素是按照key的hash值无序存储的。 但是,有时候我们却需要一个有序的元素顺序,Python 3.6之前,使用OrderedDict类可以做到,3.6开 始dict自身支持。 d1 {b:33, c:True, d:[1], f:234…...
Oracle数据库完整卸载的完整步骤
时间:2023-03-15来源:系统城装机大师作者:佚名 1、停止所有Oracle服务 进入计算机管理,在服务中,找到oracle开头的所有服务,右击选择停止。 快捷键:ctrlshiftesc打开任务管理器 文章来源 Or…...
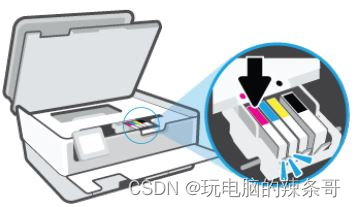
HP OfficeJet Pro 8020 如何更换碳粉盒
环境: HP OfficeJet Pro 8020 问题描述: HP OfficeJet Pro 8020 如何更换碳粉盒 解决方案: 更换碳粉盒 更换所有墨水不足的碳粉盒或空碳粉盒。 1.打开前挡盖,然后提起碳粉盒检修门。 打开打印机门 2.等待笔架停止后再继续操作…...
【Javascript】基础数据类型
目录 基础数据类型 1.number 字面量声明 数字对象方式声明 整数判断 指定返回小数位数 NaN-表示非数字值 浮点精度 解决误差 String 字面量声明 数字对象声明 连接运算符 获取长度 大小写转换 转换成大写 转换成小写 编辑 移除空白 获取单字符 编辑 截…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...
