计算机组成原理 new07 真值和机器数 无符号整数 定点整数 定点小数 $\color{red}{Δ}$
文章目录
- 真值和机器数
- 无符号整数
- 无符号整数的定义
- 无符号整数的特征
- 无符号整数的表示范围
- 无符号整数的加法
- 无符号数的减法
- 有符号整数(定点整数)
- 有符号整数的定义
- 原码
- 原码的特点
- 反码
- 反码的特点
- 补码
- 补码的特点
- 快速求解n位负数补码的方法
- 为什么补码能够多表示一个范围(重点)
- 变形补码
- 移码
- 移码的特点
- 有符号数,无符号整数的范围表示
- 判断两个数的和是否溢出
- 无符号数和有符号数如何进行减法运算
- 原码,反码,移码,补码的互相转换
- 定点小数
- 定点整数和定点小数的原码定义
- 定点小数和定点整数的补码定义
- 移码的定义(目前还不懂)
- 可表示的不同数字的个数 和 可表示范围
- 原码,反码,补码表示的定点小数个数
- 负数反码和补码比较大小的方式(重要)
- 一个数什么时候可能会溢出
- 关于原反补运算的特点
- 十六进制数的取反
真值和机器数
真值:在日常的书写习惯中,往往用正、负号加绝对值表示数值,用这种形式表示的数值为真值。例如100D,-50D,-76O。
机器数:在计算机内部版使用的数,并且最高位表示符号的二进制数,又分为有符号数和无符号数。
无符号整数
无符号整数的定义
无符号整数:无符号整数即最高位不表示符号位,每一位都是数值位。
无符号整数的特征
无符号整数一般用来表示地址或者指针,因为地址不具有负的概念。
无符号整数的表示范围
n位的无符号整数可表示 0 \color{red}{0} 0~ 2 n − 1 \color{red}{2^n-1} 2n−1的范围。
无符号整数的加法
无符号整数的加法,和普通的二进制加法没什么区别。
无符号数的减法
假设我们的mod是18,那么假设一个数是x,其在mod18下的补数就是18-x。
通过这种手段,我们可以将减法变成加法:前提是被减数>减数,即不溢出的情况下,可以得到正确的答案:例如9-3=[9+(18-3)]mod18=(9+15)mod18=(24)mod18=6。
而在无符号数的加法中,寄存器的位数实际上就已经充当了mod的作用,例如n位那么mod就是 2 n \color{red}{2^n} 2n。
通过将B全部位取反,末尾加1我们就可以得到B的补数。这个过程就和得到补码C对应-C的补码的过程一样。
其中通过这种方式得到补数的原理是这样的:因为A+A的补数=mod。
而B全部位取反+B就等于一个全1的序列,那么再将上1,自然就等于mod了。
所以取反+1就为补数。
有符号整数(定点整数)
有符号整数的定义
定点整数:定点整数是纯整数,简单来说就是不含小数,小数点在数值位之后。
若数据X的表示形式为X=x 0 , x 1 x 2 . . . x n \color{red}{x_0,x_1x_2...x_n} x0,x1x2...xn其中 x 0 \color{red}{x_0} x0是符号位,剩下的数值位 x 1 \color{red}{x_1} x1~ x n \color{red}{x_n} xn是尾数, x n \color{red}{x_n} xn为最低有效位。
有符号整数分为:原码,反码,补码,移码。
原码
原码:最高位表示符号位,具有位权,可表示整数和小数。

原码的特点
优点:和真值的对应关系简单,直观,与真值的转换简单,用原码实现乘除运算比较简便,无论是正数原码还是负数原码,比较大小很容易判断。
缺点:
1.0的表示不唯一,有两种方式表示真值0,分别是(+0)00000000和(-0)10000000
2.加减法运算比较复杂,这很好理解,如果不复杂当前计算机就不会使用补码运算了。
3.符号位不可以参与运算
反码
反码:最高位表示符号位,正数反码具有位权,负数反码无位权,可表示整数和小数。
反码的特点
缺点:
1.0的表示不唯一,00000000(+0)和11111111(-0)
2.表示范围比补码小,在计算机中很少使用,一般用作数码变换的中间形式(其实也就是原反补变换的中间形式)
4.符号位不可以参与运算
补码
最高位表示符号位,正数补码具有位权,负数补码无位权。可表示整数和小数。
补码的特点
优点:
0的表示唯一,即+0(00000000)
符号位和数值位可以参与运算
缺点:
负数补码不容易判断大小。
快速求解n位负数补码的方法
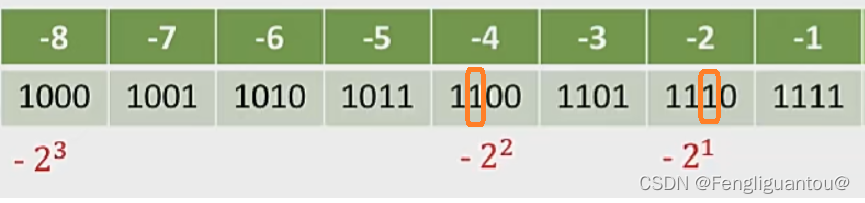
这里的最高位就是符号位,因为负数补码的符号位固定为1,所以假设总共有4位。可以看出真值 − 2 n \color{red}{-2^n} −2n的补码就是按照权重找到对应位,然后将这一位和这一位左边全置1就能得到。
并且还能看出一个特征,即负数补码的数值位越大,真值越大。
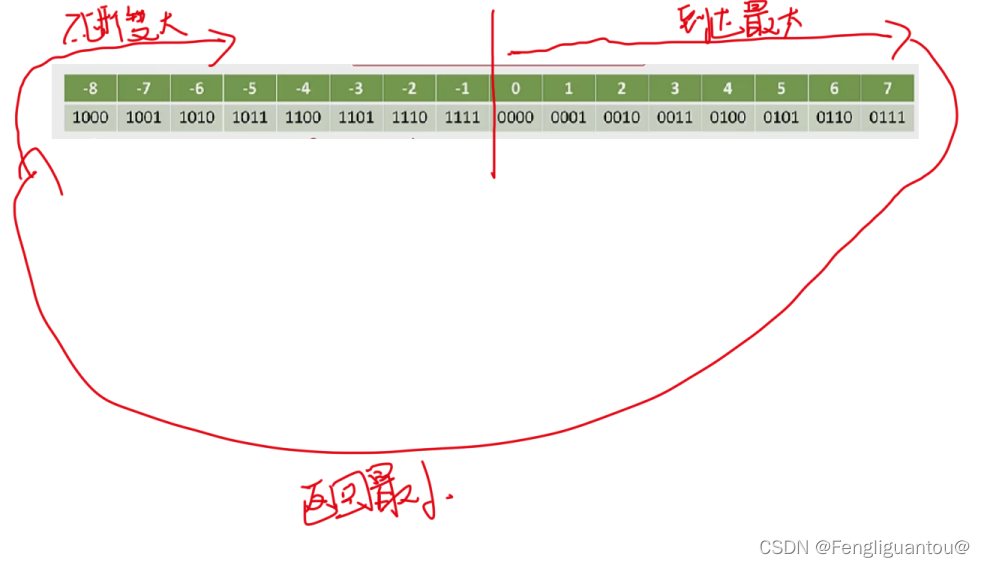
对于补码小数,上面的结论还能成立?
为什么补码能够多表示一个范围(重点)
首先,前提是机器字长为8位,原码和反码在表示过程中是一一对应的,但是两者都具有一个冗余状态,原码的1000000和反码的11111111,这两个冗余状态通过原反补转换成补码时,因为溢出原因会变成0000 0000,这就导致补码中的0只有一种表示方式,这就导致补码的1000 0000这个状态没有数字可以表示,但是通过原反补的规则,因为溢出问题的存储,原码和反码的任何一个状态都不可能转换为1000 0000,所以计算机规定原码为1000 0000和反码的1111 1111转换为补码时,直接映射成1000 0000,补码的1000 0000不需要经过原反补转换,解释的时候直接解释为1000 0000。
变形补码
移码
移码:不具有位权,常用来表示浮点数的阶码,只能表示整数。
移码的特点
优点:
1.只有一种方式表示0,即(+0)1000 0000。
2.符号位为1表示真值为正,符号位为0表示真值为负。
3.从下面这个图可以看出,移码的递增有点类似无符号整数,所以移码很方便硬件电路对比大小。
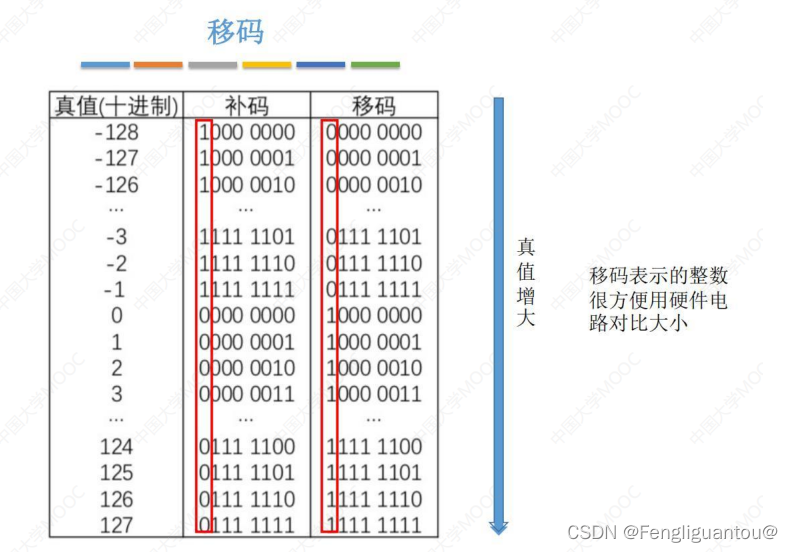
x的移码和-x的移码转变似乎也是全部位按位取反,末尾加1,这个不知道准不准确。
有符号数,无符号整数的范围表示
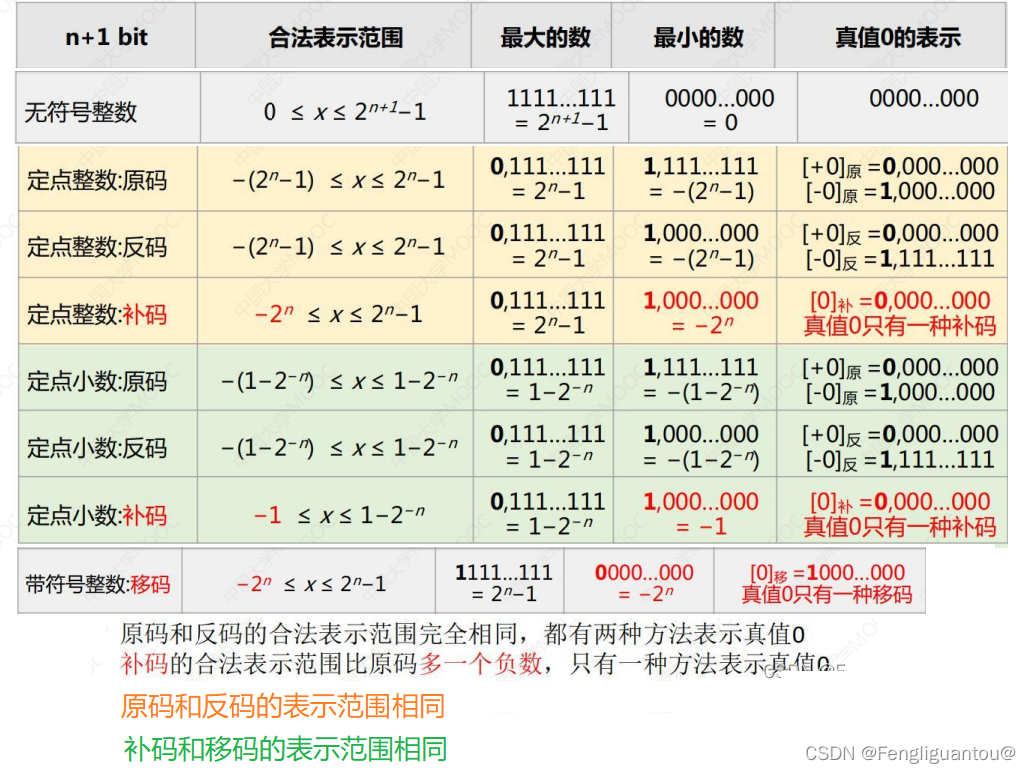
注意:定点小数虽然说能够表示这么大的范围,但是不是范围里的每个数字都能够使用定点小数准确表示出来,因为其不是和定点整数一样从0开始每次递增的。
定点整数中,补码比原码和反码多表示一个 − 2 n \color{red}{-2^n} −2n,注意是只多表示这一个数字,因为二进制整数每次的差距至少为
1
定点小数中,补码比原码和反码同样也只是多表示了-1这一个数字。
一定要注意,这里是只,不论是定点整数还是小数,补码都只是比原码多表示了一个数字。
判断两个数的和是否溢出

题目一:机器字长8位,两个数字用原码表示,A是原码表示的-64,B是原码表示的-64,两者的结果同样用原码表示,是否会溢出?
答案是会的,因为原码只能表示-127-127
题目二:机器字长8位,两个数字用补码表示,A是补码表示的-64,B是补码表示的-64,两者的结果同样用补码表示,是否会溢出?
答案是不会,因为补码可以表示-128,127
无符号数和有符号数如何进行减法运算
无论是无符号整数,还有补码, 在求-x的时候,都是如下的操作。

方法:将减数进行求补,然后将负号改为正号,被减数和求补以后的减数相加。
求补有两种方法:
方法一:全部位按位取反,末尾+1
方法二:从右往左找到第一个1,将这个1左侧的所有位(不包括这个1)全部取反。
为什么要使用加法电路来完成减法?
加法电路造价便宜,判断比较容易。
事实上,无符号的减法我们不是一定要通过上述方式完成,因为无符号是不具有符号位的,上述方式是计算机内部无符号的计算方式,如果是我们手算,我们可以直接两个数相减即可。不用进行什么取补然后减法变加法的操作。
原码,反码,移码,补码的互相转换
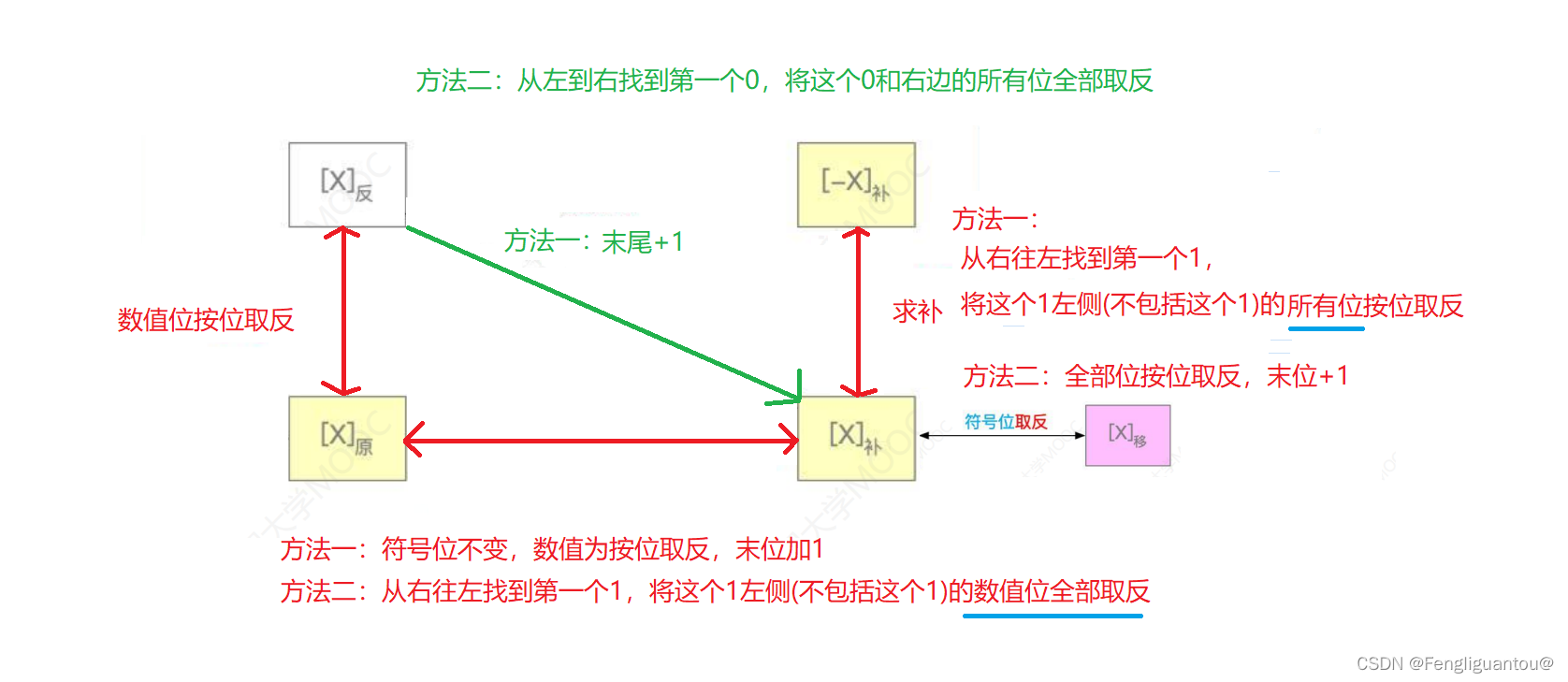
定点小数
定点小数:定点小数是纯小数,简单来说就是不含整数,小数点在符号位之后,数值位之前。若数据X的表示形式为X= x 0 , x 1 x 2 . . . x n \color{red}{x_0,x_1x_2...x_n} x0,x1x2...xn其中 x 0 \color{red}{x_0} x0是符号位,剩下的数值位 x 1 \color{red}{x_1} x1~ x n \color{red}{x_n} xn是尾数, x 1 \color{red}{x_1} x1为最高有效位。
定点整数和定点小数的原码定义
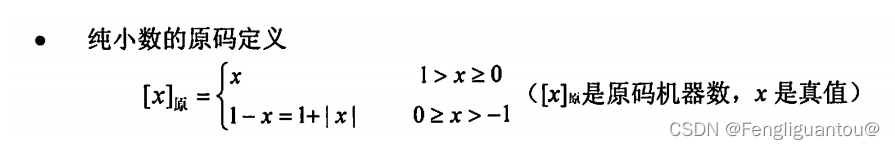
纯小数(假设机器字长为n+1位):
当 x ≥ 0 \color{red}{x \geq 0} x≥0 时,当 x ≥ 0 \color{red}{x \geq 0} x≥0 时, x \color{red}{x} x的原码可由真值 x \color{red}{x} x通过二进制转换得到。
当 x ≤ 0 \color{red}{x \leq 0} x≤0 时, x \color{red}{x} x的原码需要由 1 + ∣ x ∣ \color{red}{1+|x|} 1+∣x∣以后的真值通过二进制转换得来。
当真值等于0的时候,因为定点小数的原码具有两种形式,所以同样可以使用上述两种方式,分别是0000000和10000000
例如:
当机器字长为8位时,当x=0.5时,其原码由0.5转换而来,结果为0.1000000
当x=-0.5时,其原码由1-(-0.5)=1+0.5=1.5转换而来,结果为1.1000000
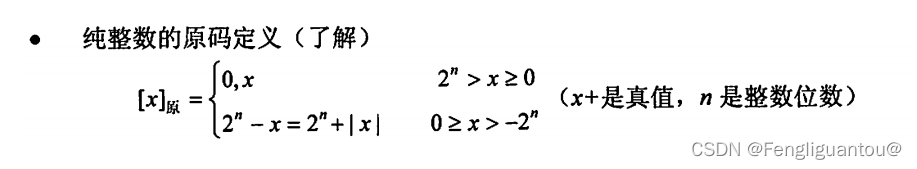
纯整数(假设机器字长为n+1位):
当 x ≥ 0 \color{red}{x \geq 0} x≥0 时, x \color{red}{x} x的原码可由真值 x \color{red}{x} x通过二进制转换得到。
当 x ≤ 0 \color{red}{x \leq 0} x≤0 时, x \color{red}{x} x的原码需要由 2 n + ∣ x ∣ \color{red}{2^n+|x|} 2n+∣x∣以后的真值通过二进制转换得来。
真值为正时,很好理解,可以直接通过二进制转换得到原码。
真值为负时,因为符号的原因,所以需要对真值取绝对值并且加上 2 n \color{red}{2^n} 2n,其本质就是加上二进制最高位的符号位。
当真值等于0时,因为定点原码的真值具有两种表现形式,00000000和1000000所以真值0变成原码的时候也可以使用上述两种方式。
例如:
当机器字长为8时,当x=5时,5的原码由真值5转换得来,结果为为0.0000101
当x=-5时,-5的原码由 2 8 − ( − 5 ) = 2 8 + 5 \color{red}{2^8-(-5)=2^8+5 } 28−(−5)=28+5真值转换而来,结果为
1.0000101
总结:
真值为正时,原码可以由真值直接转换得来。
真值为负时,需要对真值取绝对值并加上对应机器字长二进制对应的符号位,小数就直接加上1即可,整数就加上二进制最高位对应的真值。然后用真值转换成原码。
本质都是通过真值加上某个数,从而修改对应二进制的符号位,将符号位的0变成1。
这里的定义,其实本质上就是如果通过真值,不考虑符号位的情况下,直接转换二进制得到对应的原码。因为实际上真值为负时,我们可以通过符号位取1的方式,然后按照原反补的方式得到原码,而这种定义方式就是不靠这种方法,因为最终通过定义,真值变成了正数,这时候就不需要考虑符号位了,并且因为正数的原反补相同。
定点小数和定点整数的补码定义
假设机器字长为n+1位。
定点整数的补码定义:
当真值为正时,补码直接由真值通过二进制转换得到
当真值为负时,补码需要由 2 n + 1 − ∣ 真值 ∣ \color{red}{2^{n+1}-|真值| } 2n+1−∣真值∣的结果通过二进制转换得到。
实际上就是mod-真值的绝对值。当有n位时,mod就是 2 n \color{red}{2^n} 2n

这里的定义,其实本质上就是如果通过真值,不考虑符号位的情况下,直接转换二进制得到对应的补码。因为实际上真值为负时,我们可以通过符号位取1的方式,然后按照原反补的方式得到补码,而这种定义方式就是不靠这种方法。因为最终通过定义,真值变成了正数,这时候就不需要考虑符号位了,并且因为正数的原反补相同。
移码的定义(目前还不懂)
移码本质就是加了一个偏执常量,当机器字长为n+1时,真值为x的移码,需要由x+ 2 n \color{red}{2^{n}} 2n转换得到。这时偏执常量就是 2 n \color{red}{2^n} 2n
可表示的不同数字的个数 和 可表示范围
可表示的数字个数:是站在状态上来进行思考的,一个二进制可以表示2种状态,n个二进制位就可以表示 2 n \color{red}{2^n} 2n个状态,当然原码和反码会少1个。
可表示的范围:是站在位权来进行考虑的,因为二进制的位权是从0开始,只有正/负原码,正数反码和补码可以这样计算使用位权来计算范围。但是负数的补码和反码不能这样计算范围,因为其没有位权这个。
原码,反码,补码表示的定点小数个数
假设机器字长为n+1,站在状态的角度上,可以表示 2 n + 2 n \color{red}{2^n+2^n} 2n+2n个状态,但是由于0有两种表示,所以有状态重叠,所以只能表示 2 n + 2 n = 2 n + 1 − 1 个不同数字 \color{red}{2^n+2^n=2^{n+1}-1个不同数字} 2n+2n=2n+1−1个不同数字,反码也是如此。
补码因为没有状态重叠,所以可以表示 2 n + 1 \color{red}{2^{n+1}} 2n+1个不同的状态。
负数反码和补码比较大小的方式(重要)
负数反码和原码比较只需要遵循一个原则:数值位越大,真值越大。
一个数什么时候可能会溢出
一个数只有在全1的时候再加1或者大于1的数才会溢出。
关于原反补运算的特点
实际上正数原码和反码,补码的符号位都可以参与运算,因为补码的符号位可以参与运算,所以正数原码和反码也可以,但是负数的原码和反码无法做到符号位参与运算,所以计算机中的加减法在不对符号位处理的前提下只能由补码完成。
十六进制数的取反
十六进制数数位的取反=15-该数位的数字
例如F1取反以后变成0E。
相关文章:

计算机组成原理 new07 真值和机器数 无符号整数 定点整数 定点小数 $\color{red}{Δ}$
文章目录 真值和机器数 无符号整数无符号整数的定义无符号整数的特征无符号整数的表示范围无符号整数的加法无符号数的减法 有符号整数(定点整数)有符号整数的定义原码原码的特点反码反码的特点补码补码的特点快速求解n位负数补码的方法为什么补码能够多表示一个范围(重点)变形…...
基于SSM的文化培训学校网站的设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...

gitee-git使用
克隆gitee某代码仓库某分支流程 1.克隆远程gitee仓库某分支到本地 2.如果克隆gitee仓库是私有的系统会弹出弹框让你输入gitee的账户和密码 3.克隆远程分支完成 git所需命令 克隆远程仓库到本地 git clone 仓库URLgit克隆远程分支到本地 git clone -b 分支名 仓库URLgit 拉…...
)
欧拉图(Euler Graph)
这种「一笔画」问题与欧拉图或者半欧拉图有着紧密的联系,下面给出定义: 通过图中所有边恰好一次且行遍所有顶点的通路称为 欧拉通路; 通过图中所有边恰好一次且行遍所有顶点的回路称为 欧拉回路; 具有欧拉回路的无向图称为 欧拉图; 具有欧拉通路但不具有欧拉回路的无向图…...

【安全体系架构】——零信任网络架构
什么是零信任网络架构? 零信任网络架构是一种网络和信息安全模型,它将传统的信任模型颠覆,不再信任内部或外部用户、设备或网络。相反,它将每个访问请求都视为不受信任,要求对每个用户、设备和流量都进行认证和授权&a…...

mybatis动态sql一对多查询
在数据库设计中,一对多关系是非常多的,例如消息通知和附件,一个消息通知中往往会包含多个附件,这种情况下使用mybatis动态sql可以很方便的查询出来。 1、数据库设计 消息表:sys_message CREATE TABLE sys_message (i…...
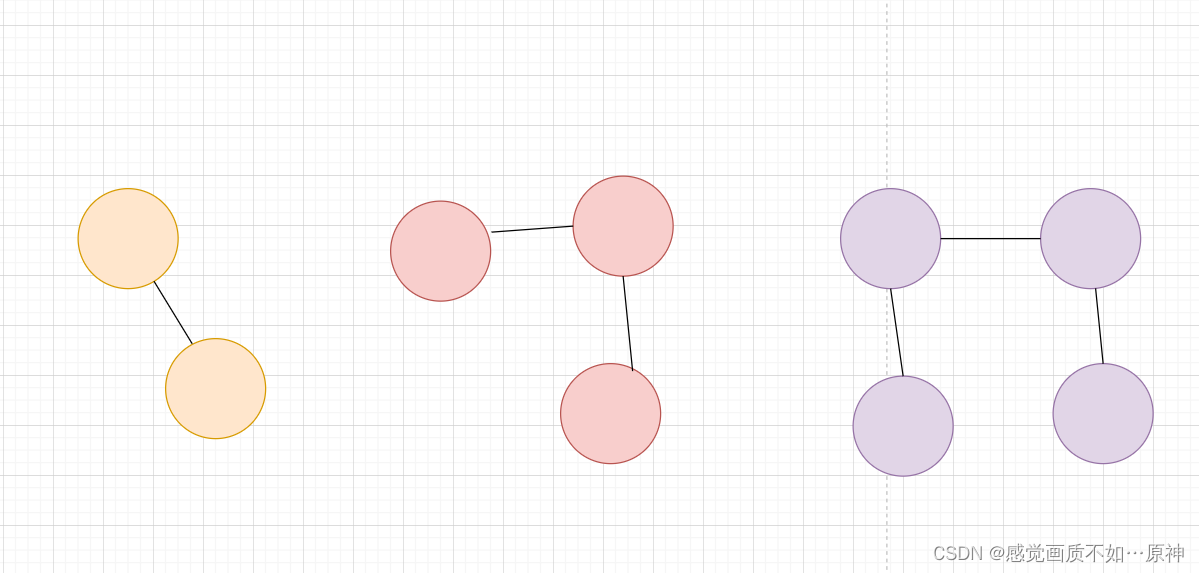
Leetcode.2316 统计无向图中无法互相到达点对数
题目链接 Leetcode.2316 统计无向图中无法互相到达点对数 rating : 1604 题目描述 给你一个整数 n n n ,表示一张 无向图 中有 n n n 个节点,编号为 0 0 0 到 n − 1 n - 1 n−1 。同时给你一个二维整数数组 e d g e s edges edges ,其…...

介绍机器学习中CatBoost工具的详细使用指南
在机器学习的动态世界中,Python 是创新背后的驱动力,专业人士必须使用正确的工具。CatBoost 就是这样一个工具,以其卓越的速度和准确性悄然改变了该领域。在本指南中,我们将深入研究 Python 3 中的 CatBoost,涵盖基础知识、高级技术和实际示例,包括使用示例数据集和绘图进…...

操作系统【OS】线程与进程的比较
进程 线程 是什么的单位? 是资源分配的基本单位 是调度的基本单位 不能共享什么? 不能共享虚拟地址空间 不能共享栈指针 可以共享什么? 拥有一个完整的资源平台 每个进程都有独立的地址空间和资源 除了共享全局变量,不允许其他进程访问 某进程中的线程…...
在Mac上使用安卓桌面模式
在安装Homeblew的基础上 替换国内源 export HOMEBREW_API_DOMAIN"https://mirrors.tuna.tsinghua.edu.cn/homebrew-bottles/api" export HOMEBREW_BREW_GIT_REMOTE"https://mirrors.tuna.tsinghua.edu.cn/git/homebrew/brew.git" brew update 安装Scrcpy …...

YOLO目标检测——人脸口罩佩戴数据集【(含对应voc、coco和yolo三种格式标签】
实际项目应用:公共场所监控场景下的大密度人群检测是否佩戴口罩,以及戴口罩的人证比对(安检刷脸不用摘口罩)、手机解锁、刷脸考勤等身份认证场景。数据集说明:人脸口罩佩戴检测数据集,真实场景的高质量图片…...
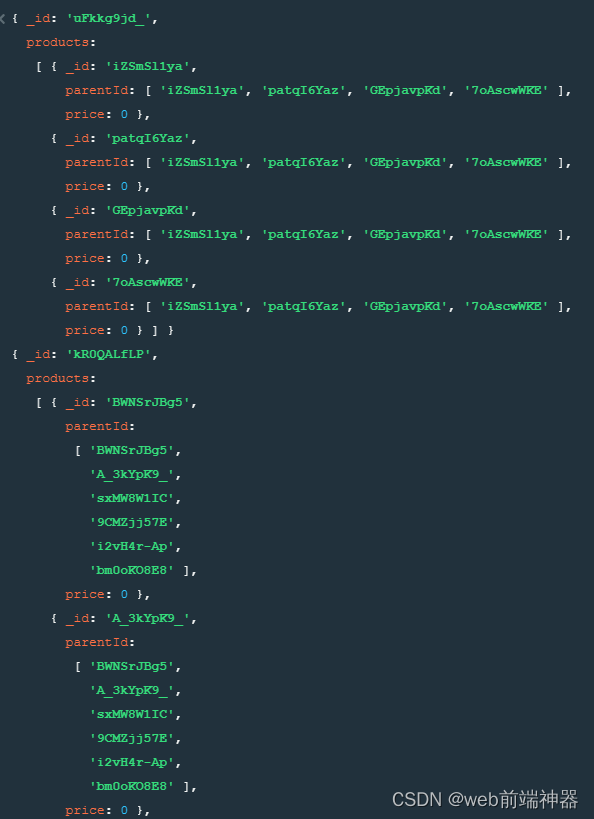
mongodb如何多表查询,如同时查询店铺以及里面对应的商品
多表查询场景介绍 一种很常见的场景,比如电商首页中,需要同时展示最近比较火热的店铺,以及直接展示店铺里对应的商品。或者用户下单之后购物车里可以看到所选的商品以及对应的店铺。如果不知道如何用mongodb自带的查询语句快速查询的话&#…...

Linux环境修改服务器时间和网络时间保持一致
目录 介绍UTC和CST 修改时区 修改时间 介绍UTC和CST UTC是协调世界时,是全球统一的时间标准。UTC的时间是基于原子钟计算的,以秒为单位,不受夏令时等影响。世界各地都可以通过UTC来同步时间。 CST是中央标准时间,相当于UTC-6…...

CUDA学习笔记6——事件计时
事件计时 CUDA事件是直接在GPU上实现的,因此它们不适用于对同时包含设备代码和主机代码的混合代码计时。 cudaEventCreate 创建一个事件cudaEventRecord 记录一个事件cudaEventElapsedTime 计算两个事件之间经历的时间,第一个参数为某个浮点变量的地址…...

使用vscode调试ffmpeg源码
ffmpeg的编译配置 # --enable-debug 设置为调试级别 # --disable-stripping 如果不加此选项,会strip去掉符号信息 ./configure --prefix{output_path} --enable-debug --disable-stripping make -j10VSCode的配置 将以下文件对比替换工程.vscode目录下的相同文件 …...

微信小程序--数字化会议OA系统之首页搭建
一、Flex弹性布局 布局的传统解决方案,基于盒状模型,依赖 display属性 position属性 float属性。它对于那些特殊布局非常不方便,比如,垂直居中就不容易实现。 2009年,W3C提出了一种新的方案—-Flex布局,可…...
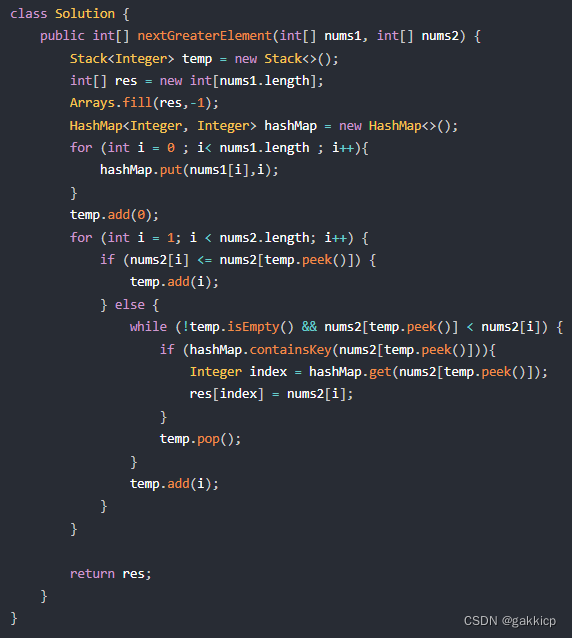
代码随想录算法训练营第六十天 | 739. 每日温度、496.下一个更大元素 I
739. 每日温度 链接: 代码随想录 (1)代码 496.下一个更大元素 I 链接: 代码随想录 (1)代码...

WebView 以及如何测试
混合应用 顾名思义,它们是本机应用程序和 Web 应用程序的混合体。它们可以在应用程序商店中下载,并且需要像本机应用程序一样从设备进行访问身份验证,但它们也有一个嵌入在应用程序中的浏览器(WebView)用于呈现 HTML。…...

Jetpack:013-Jetpack底部导航栏
文章目录 1. 概念介绍2. 使用方法2.1 NavigationBar2.2 NavigationBarItem 3. 示例代码3.1 代码和注释3.2 代码难点3.3 运行效果 4. 内容总结 我们在上一章回中介绍了Jetpack中弹出菜单相关的内容,本章回中将介绍 底部导航栏。闲话休提,让我们一起Talk …...

MATLAB - excel 读取
matlab中excel 读取 1. 写入excel文件 - xlswrite2. 读取excel文件 - xlsread 1. 写入excel文件 - xlswrite xlswrite(filename,A,sheet,xlRange) % 写入字符串 % 注意事项:Str需要是Cell格式,否则一个字母占一格 % Str {‘abc’}; xlswr…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...

第22节 Node.js JXcore 打包
Node.js是一个开放源代码、跨平台的、用于服务器端和网络应用的运行环境。 JXcore是一个支持多线程的 Node.js 发行版本,基本不需要对你现有的代码做任何改动就可以直接线程安全地以多线程运行。 本文主要介绍JXcore的打包功能。 JXcore 安装 下载JXcore安装包&a…...

【汇编逆向系列】六、函数调用包含多个参数之多个整型-参数压栈顺序,rcx,rdx,r8,r9寄存器
从本章节开始,进入到函数有多个参数的情况,前面几个章节中介绍了整型和浮点型使用了不同的寄存器在进行函数传参,ECX是整型的第一个参数的寄存器,那么多个参数的情况下函数如何传参,下面展开介绍参数为整型时候的几种情…...

SOC-ESP32S3部分:30-I2S音频-麦克风扬声器驱动
飞书文档https://x509p6c8to.feishu.cn/wiki/SKZzwIRH3i7lsckUOlzcuJsdnVf I2S简介 I2S(Inter-Integrated Circuit Sound)是一种用于传输数字音频数据的通信协议,广泛应用于音频设备中。 ESP32-S3 包含 2 个 I2S 外设,通过配置…...


