数据结构----算法--五大基本算法(这里没有写分支限界法)和银行家算法
数据结构----算法–五大基本算法(这里没有写分支限界法)和银行家算法
一.贪心算法
1.什么是贪心算法
在有多个选择的时候不考虑长远的情况,只考虑眼前的这一步,在眼前这一步选择当前的最好的方案
二.分治法
1.分治的概念
分治法:分而治之
将一个问题拆解成若干个解决方式完全相同的问题
满足分治的四个条件
1.问题难度随着数据规模缩小而降低
2.问题可拆分
3.子问题间相互独立
4.子问题的解可合并
2.典型的分治:二分查找(折半搜索) BinaryChop
前提:有序
时间复杂度O(log2的n次方)
1.循环实现二分查找
//循环
int BinaryChop1(int a[], int begin, int end ,int find) {if (a == nullptr || begin > end) return -1;while (begin<= end) {int mid = begin+(end- begin)/2 ;if (a[mid] == find) {cout << "找到了,返回在数组中的下标" << endl;return mid;}else if (a[mid] < find) {begin = mid + 1;}else if (a[mid] > find) {end = mid - 1;}}return -1;
}
2.递归实现二分查找
//递归
int BinaryChop2(int a[], int begin, int end, int find) {if (a == nullptr || begin > end) return -1;int mid = begin+(end- begin)/2;if (a[mid] == find) {cout << "找到了,返回数组下标" << endl;return mid;}else if (a[mid] < find) {begin = mid + 1;}else if (a[mid] > find) {end = mid - 1;}return BinaryChop2(a, begin, end, find);}
三.回溯法
1.回溯法解决的问题
1.求子集的问题
2.求排列的问题
3.求集合的问题
4.求棋盘的问题
2.回溯常见的写法
循环嵌套递归
3.用回溯法解决一道全排列的问题(此题的网址为https://leetcode.cn/problems/permutations/)
此题在之前的博客中具体分析过(博客的网址如下https://blog.csdn.net/m0_73483024/article/details/133589061?spm=1001.2014.3001.5502)
题目:
四.动态规划(Dynamic Programming)
1.动态规划可以解决的问题
动态规划可以用来求最优解(最大、最小、最多等)的问题
2.动态规划操作对象所要满足的性质
大问题可以拆解成解决方案完全相同的子问题,并且要满足以下两个性质
1.满足最优子结构性质(子问题的最优解构成当前问题的最优解)
2.无后效性(一旦某一状态被确定,那么过去这个状态如何求得的我们就再也不关注了)
3.动态规划的求解过程
1.拆分
2.定状态(子问题的最优解)
3.做决策
4.求状态转移方程
4.动态规划的实现手段
1.自顶向下带备忘的解法(大到小)
2.自底向上的解法(小到大)
注意:动态规划的空间消耗是用来换时间了
5.关于动态规划的问题
1.凑钱问题
题目:
有1元,3元,5元面额的钞票,想要凑到n元钱
解决方法:
创建一个f数组
f(n)表示想要凑到n元钱所需要的最小的钞票数
我们观察下面式子,找出规律
f(0)=0
f(1)=f(1-1)+1=1
f(2)=f(2-1)+1=2
f(3)=min{f(3-3)+1=1,f(3-1)+1=3}=1
f(4)=min{f(4-3)+1=2,f(4-1)+1=2}=2
f(5)=min{f(5-5)+1=1,f(5-3)+1=3,f(5-1)+1=3}=1
推导出动态转移方程得
f(i)=min{f(i-v[j])}+1(v[j]<=i)
这里v是一个存1元,3元,5元面额的钞票的数组,j是遍历v数组的变量
2.一维的动态划分问题:最长递增子序列(LIS)
题目:
有一个数组中有6、3、9、8、4、7、2、5、10、1这些元素,找到这个数组中的最长递增子序列
解决方法:
方法一
创建一个f数组
f(n)表示n下标与前序元素构成的LIS的长度
我们观察下面式子,找出规律
f(0)=1
f(1)=1
f(2)=max{9>3 f(1)+1=2
9>6 f(0)+1=2
1(只有自己本身,长度为1)
}=2
f(3)=max{8>3 f(1)+1=2
8>6 f(0)+1=2
1(只有自己本身,长度为1)
}=2
f(4)=max{4>3 f(1)+1=2
1(只有自己本身,长度为1)
}=2
f(5)=max{7>4 f(4)+1=3
7>3 f(1)+1=2
7>6 f(0)+1=2
1(只有自己本身,长度为1)
}=3
推导出动态转移方程得
f(i)=max(f(j)+1,1) (v[j]<v[i],0<=j<i)
这里v是数组,i和j是遍历v数组的变量
方法二(相较于方法一优化)
创建一个数组用来存等长LIS右边界的最小值(下标当作长度)
从左到右遍历数组,对创建的数组进行更新,最后数组的使用量就是最长递增子序列的长度
看下面进行理解
f(0)=1
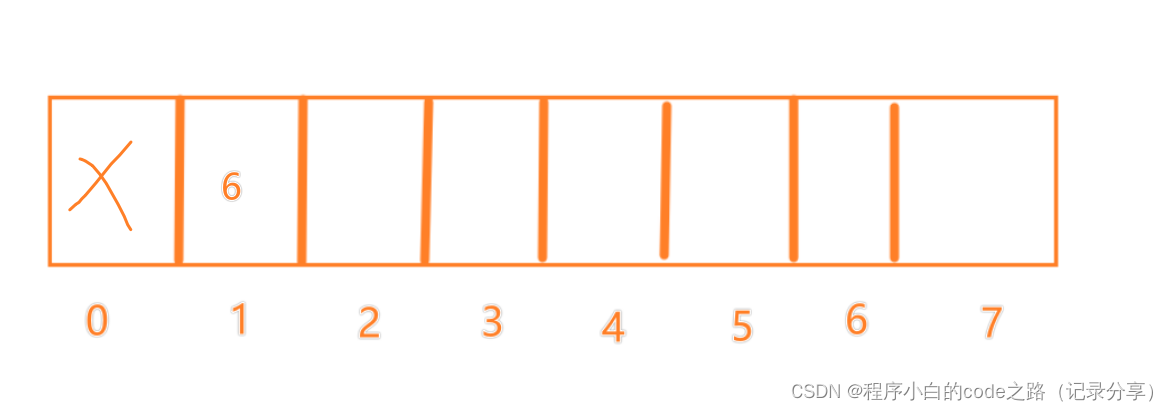
f(1)=1
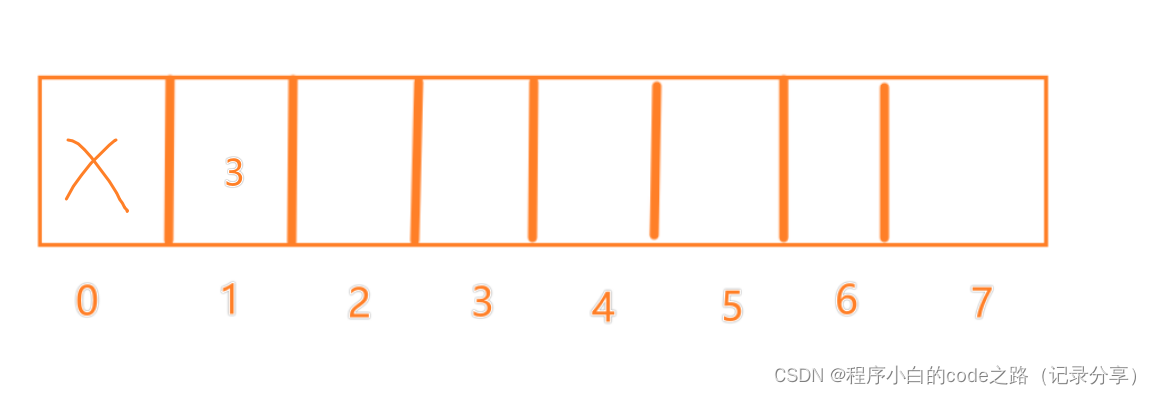
f(2)=2
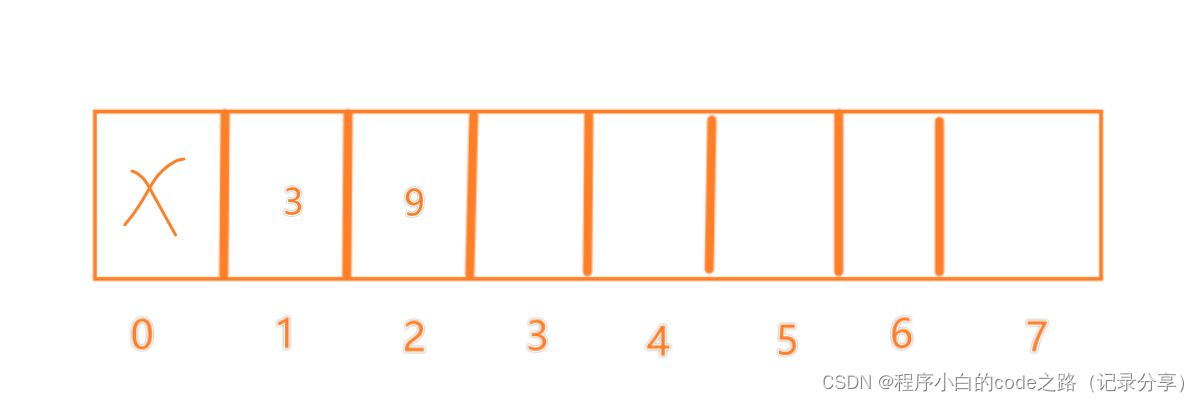
f(3)=2
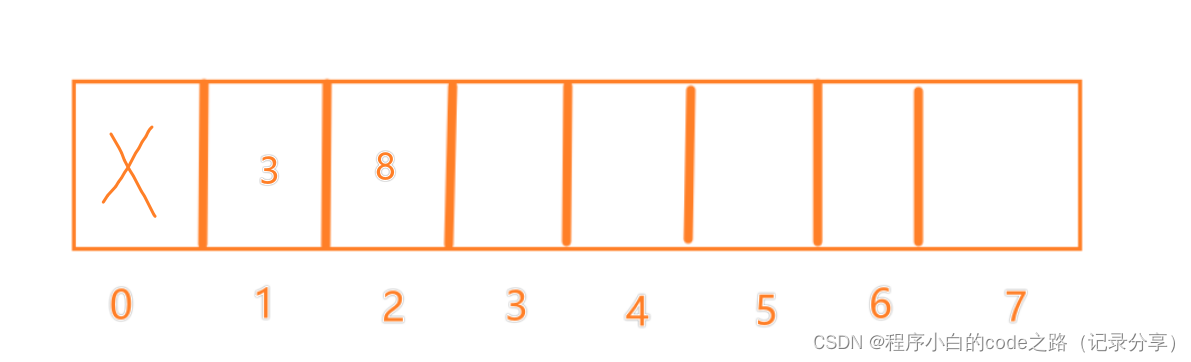
f(4)=2
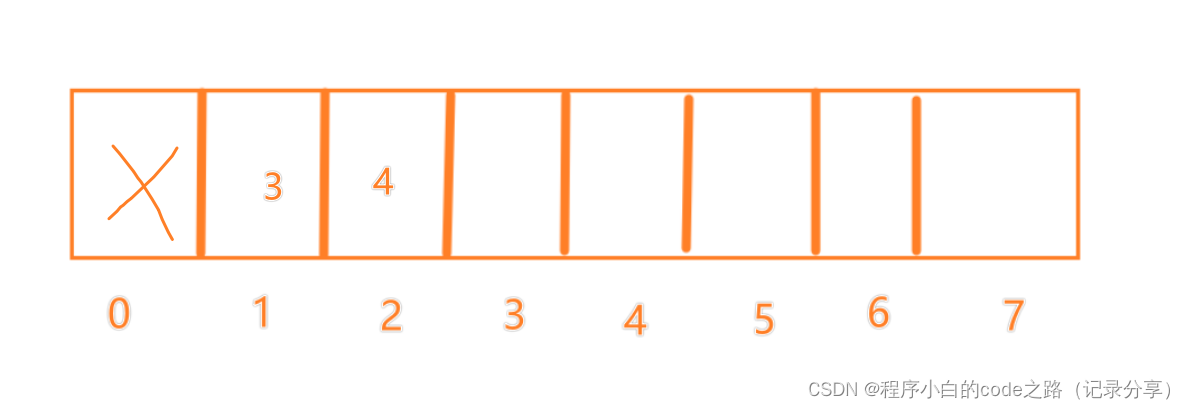
f(5)=3
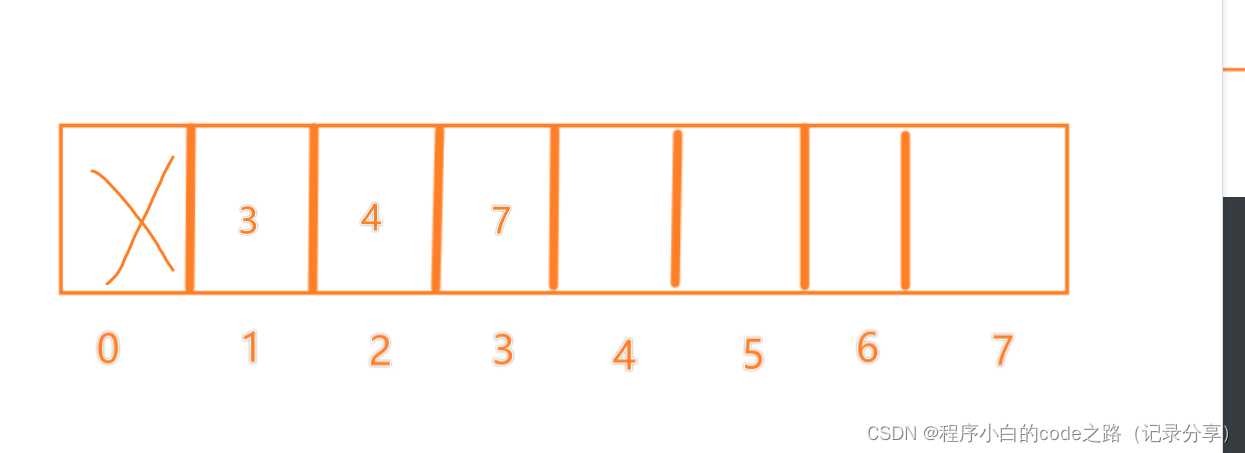
下面的过程就不再写了
方法三(在方法二的基础上,进行二分搜索,在进行数组的更新时使用二分搜索)
3.二维的动态规划问题:捡苹果
题目:
有一个m*n的格子,每个格子中有数量不一的苹果,一个小机器人(只能往右或者往下走)从左上角走到它不能再走了,求它最多能捡到多少个苹果
解决:
状态转移方程为 c[i] [j]=max{c[i-1] [j],c[i] [j-1]}+A[i] [j]
c数组存的是到每个位置所能捡到的最大苹果数量,A数组存的是每个位置的苹果数量
4.二维的动态规划问题且带附加条件的:最长公共子序列(LCS)
题目:
求X数组{A,B,B,D,C,B,C}与Y数组{B,C,D,B,A,C}的最长公共子序列
解决:
状态转移方程为 c[i] [j]={c[i-1] [j-1]+1 xi==yi
max{c[i-1] [j],c[i] [j-1]}} xi!=yi
}
c数组存的是x数组走到数组中的某个元素和y数组走到数组中的某个元素时,二者所构成的LCS的长度
c[i] [j]存的是x数组走到第i个元素,y数组走到第j个元素,二者所构成的LCS的长度
四.博弈树
1.博弈树(Game Tree)
棋类中用到的博弈树满足的条件
1.二者零和
2.全信息
3.非偶然
注意:博弈树要在时间消耗和结果准确度中做一个平衡
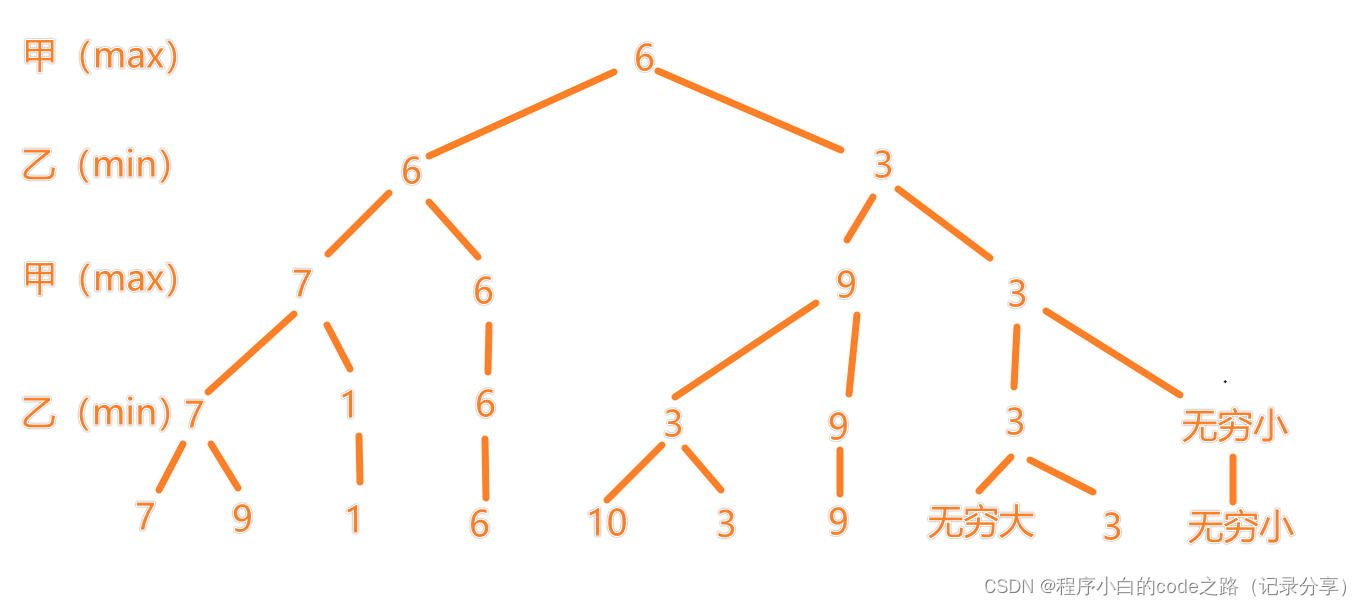
2.极大极小搜索树(是在原有博弈树的基础上实现的)
看下面这张图理解博弈树
甲是自己要选择尽量大的
乙是对手要使我们最小,所以乙选择尽量小的
3.α-β剪枝(对极大极小树的优化)
看下面图片(都是部分图,不是完整的)理解α-β剪枝
图片一
注意:这是一个深搜过程(图中数字表示处理的步骤)
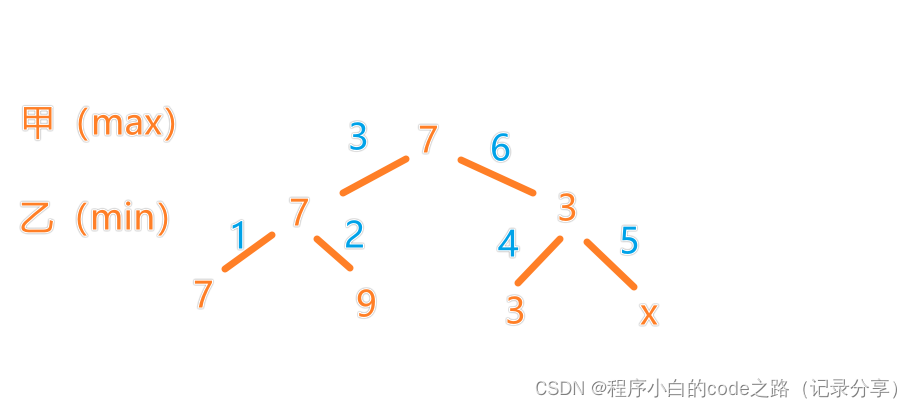
当此图第4步得到的值小于第3步得到的值,那么第5步就不用处理了
图片二
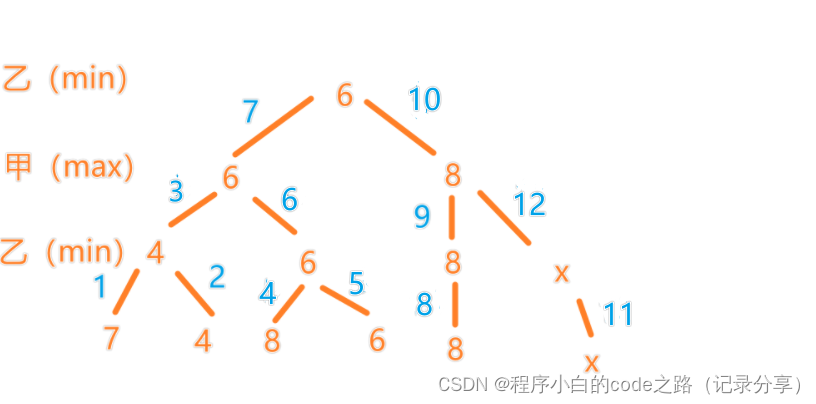
注意:这是一个深搜过程(图中数字表示处理的步骤)
当此图第9步得到的值大于第7步得到的值,那么第11步和第12步就不用处理了
五.银行家算法
1.使用银行家算法要满足的条件
1.固定数量的进程共享固定数量的资源
2.进程最大请求资源数
3.单次申请的资源数不能超出可分配资源数
4.不是一次性全部申请,分批次进行
5.进程等待资源的时间是有限的(不会无休止等待)
6.当满足进程的最大资源需求,进程应该在有限时间内归还资源
2.银行家算法的操作步骤
A:总资产
B:所需的最大资源数
C:已经分配的资源数
D:仍然需要的资源数
E:每次请求的资源数
F:可分配的资源数
1.看E<=F是否满足
如果不满足就等待
如果满足就进行下一步
2.看E<=D是否满足
如果不满足,失败
如果满足就进行下一步
3.假装分配,更新各个值
C=C+E
D=D-E
F=F-E
相关文章:

数据结构----算法--五大基本算法(这里没有写分支限界法)和银行家算法
数据结构----算法–五大基本算法(这里没有写分支限界法)和银行家算法 一.贪心算法 1.什么是贪心算法 在有多个选择的时候不考虑长远的情况,只考虑眼前的这一步,在眼前这一步选择当前的最好的方案 二.分治法 1.分治的概念 分…...
【七:docken+jenkens部署】
一:腾讯云轻量服务器docker部署Jenkins https://blog.csdn.net/qq_35402057/article/details/123589493 步骤1:查询jenkins版本:docker search jenkins步骤2:拉取jenkins镜像 docker pull jenkins/jenkins:lts步骤3:…...
智能水印相机微信小程序源码
相信大家日常在生活中或者工作中都有使用过水印相机来拍照记录吧,但是又要在手机上面多下载一个APP。 那么小编今天给大家带来一款智能水印相机,拍照自动添加时间、地点、经纬度等水印文字,可用于工作考勤、学习打卡、工作取证等,…...

一、2023 CISSP认证介绍
目录 1.CISSP概况 2.CISSP考题分析 3.备考建议 1.CISSP概况 参考:...

redis 实现互相关注功能
突然想到平时的设计软件如何实现互相关注这个功能,然后查询后大致思路如下: 可以使用 Redis 数据库来存储关注关系。 在社交网络应用程序中,互相关注功能(也称为双向关注或好友关系)是一种常见的功能,允许…...

【代码随想录】算法训练营 第十一天 第五章 栈与队列 Part 2
20. 有效的括号 题目 给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。每个右括号都有一…...

mysql 启动报错 Can t change dir to xxx, No such file or directory 配置错误或挂载导致
省流: 挂载的话,使用 /etc/fstab 放fstab里会在程序启动前加载NFS文件系统,放rc.local里往往造成程序启动加载时找不到路径。 正文: 在企业中,服务器重启,有时候会遇到mysql 启动报错 Cant change dir …...

AWS SAA-C03考试知识点整理
S3: 不用于数据库功能 分类: S3 Standard :以便频繁访问 S3 Standard-IA 或 S3 One Zone-IA : 不经常访问的数据 Glacier: 最低的成本归档数据 S3 Intelligent-Tiering智能分层 :存储具有不断变化或未知访问…...
HugeGraph 部署和Hubble1.0.0的数据导入Bug修复
背景 HugeGraph 安装部署了最新版本1.0.0,发现它的 Web 工具 Hubble 有一个大 Bug。数据导入的时候,配置节点属性映射这个选项时,下拉框只有一个选项,但实际上,元数据配置中的属性有3个,这个 Bug 是怎么产…...
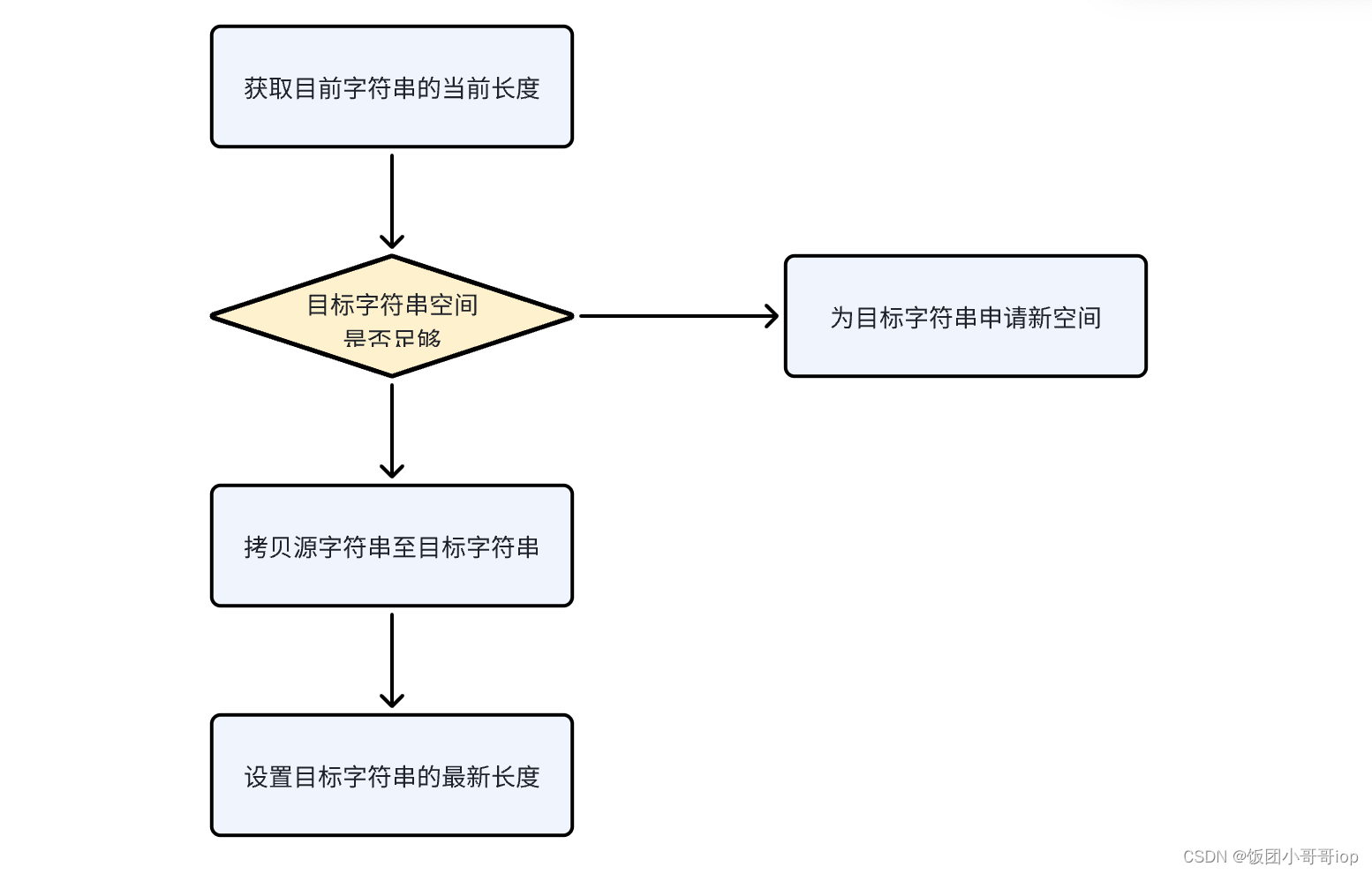
01、字符传实现为什么是SDS而不是char*?
问题: 1. sds 是什么 ? 2. sds 相对于char * 有什么好处 ?解决了哪些疑难杂症? 3. sds 有什么不足?可以优化的点? 思考下: 平常工作开发中,我们记录一条用户信息、订单信息&…...

顺应趋势,用大数据精准营销抓住大数据时代的机遇
想先问大家一个问题:“你觉得现在的营销好做吗?”想必大多数人在说到自己如何营销这一点上,都有道不完的“苦水”。“现在找客户难,投了几十万的广告费,真正来的客户却少得可怜,平均获客成本高得吓人”一位…...

面向石油和天然气的计算机视觉和深度学习1
面向石油和天然气的计算机视觉和深度学习1 1. 好处1.1 安全1.2 生产优化与估算(Production Optimization and Estimation)1.3 降低生产和维护成本(Reduce Production and Maintenance Costs) 2. 应用2.1 维护2.1.1 预测维护&#…...

微信小程序三种授权登录以及授权登录流程讲解
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《微信小程序开发实战》。🎯Ἲ…...
笔记——程序结构)
C现代方法(第10章)笔记——程序结构
文章目录 第10章 程序结构10.1 局部变量10.1.1 静态局部变量10.1.2 形式参数 10.2 外部变量10.2.1 示例:用外部变量实现栈10.2.2 外部变量的利与弊 10.3 程序块10.4 作用域10.5 构建C程序10.5.1 复杂程序:给一手牌分类 问与答写在最后 第10章 程序结构 …...

解密Web安全:Session、Cookie和Token的不解之谜
解密Web安全:Session、Cookie和Token的不解之谜 前言第一部分:什么是Session、Cookie和Token1. Session(会话):2. Cookie(HTTP Cookie):3. Token(令牌):比较: 第二部分&a…...

1016 部分A+B
#include<bits/stdc.h> using namespace std; int main(){string str1;string str2;int a,b;cin>>str1>>a>>str2>>b;int a10;int a20;for(auto t:str1){if(t-0a){a1a1*10a;}}for(auto t:str2){if(t-0b){a2a2*10b;}}cout<<a1a2; }...

搭建react项目
一、环境准备 1、安装node 官网下载安装:https://nodejs.org/en 注: npm5.2以后,安装node会自动安装npm和npx 2、安装webpack npm install -g webpack3、安装create-react-app npm install -g create-react-app二、创建react项目 1、初…...

Hive跨集群数据迁移过程
文章目录 环境数据迁移需求迁移过程记录 环境 Hive集群AHive集群B跳转机一台 数据迁移需求 本次迁移数据100G,15亿条,数据流转方向从集群A经过跳转机到集群B,通过HDFS拉取和重新建表导入的方式完成数据库迁移。 迁移过程记录 - 当前操作…...

中国移动启动算网大脑“天穹”全网试商用
10月12日,中国移动在2023全球合作伙伴大会主论坛正式启动算网大脑“天穹”全网试商用,全面开启算力网络2.0新征程,标志着中国移动算力网络迈向“融合统一”新阶段。 为落实国家“东数西算”战略,中国移动开创性提出算力网络新理念…...
apk和小程序渗透
apk和小程序域服务器通信使用的还是http协议,只是使用了加密。只要可以获取到http的请求报文,就可以回归到web渗透的层面。apk和小程序的渗透很复杂,涉及逆向时要进行脱壳,脱壳后反编译了,源代码没做加密就能直接逆向出…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果