C语言 力扣习题 10.19日 day1
1.两整数相加
给你两个整数 num1 和 num2,返回这两个整数的和。
示例 1:
输入:num1 = 12, num2 = 5
输出:17
解释:num1 是 12,num2 是 5 ,它们的和是 12 + 5 = 17 ,因此返回 17 。
示例 2:
输入:num1 = -10, num2 = 4
输出: - 6
解释:num1 + num2 = -6 ,因此返回 - 6 。
int sum(int num1, int num2)
{return num1 + num2;
}
2. 温度转换
给你一个四舍五入到两位小数的非负浮点数 celsius 来表示温度,以 摄氏度(Celsius)为单位。
你需要将摄氏度转换为 开氏度(Kelvin)和 华氏度(Fahrenheit),并以数组 ans = [kelvin, fahrenheit] 的形式返回结果。
返回数组 ans 。与实际答案误差不超过 10 - 5 的会视为正确答案。
注意:
开氏度 = 摄氏度 + 273.15
华氏度 = 摄氏度 * 1.80 + 32.00
示例 1 :
输入:celsius = 36.50
输出:[309.65000, 97.70000]
解释:36.50 摄氏度:转换为开氏度是 309.65 ,转换为华氏度是 97.70 。
示例 2 :
输入:celsius = 122.11
输出:[395.26000, 251.79800]
解释:122.11 摄氏度:转换为开氏度是 395.26 ,转换为华氏度是 251.798 。
思路与算法:
题目要求将给定摄氏度 celsius\textit{celsius}celsius 转换为开氏度和华氏度,我们根据题目给定的计算公式直接计算即可,其中计算公式如下 :
开氏度:Kelvin = Celsius + 237.15\text{Kelvin} = \text{Celsius} + 237.15Kelvin = Celsius + 237.15;
华氏度:Fahrenheit = Celsius×1.80 + 32.00\text{Fahrenheit} = \text{Celsius} \times 1.80 + 32.00Fahrenheit = Celsius×1.80 + 32.00;
double* convertTemperature(double celsius, int* returnSize)
{double* res = (double*)malloc(sizeof(double) * 2);res[0] = celsius + 273.15;res[1] = celsius * 1.80 + 32.00;*returnSize = 2;return res;
}
3.最小偶倍数
给你一个正整数 n ,返回 2 和 n 的最小公倍数(正整数)。
示例 1:
输入:n = 5
输出:10
解释:5 和 2 的最小公倍数是 10 。
示例 2:
输入:n = 6
输出:6
解释:6 和 2 的最小公倍数是 6 。注意数字会是它自身的倍数。
解法一:
int smallestEvenMultiple(int n) {if (n % 2 == 0) {return n;}else{return n * 2;}
}解法二:
int smallestEvenMultiple(int n) {int result = n % 2 == 0 ? n : 2 * n;return result;
}
解法二优化:
int smallestEvenMultiple(int n) {return n % 2 == 0 ? n : 2 * n;
}4.整数的各位积和之差
给你一个整数 n,请你帮忙计算并返回该整数「各位数字之积」与「各位数字之和」的差。
示例 1:
输入:n = 234
输出:15
解释:
各位数之积 = 2 * 3 * 4 = 24
各位数之和 = 2 + 3 + 4 = 9
结果 = 24 - 9 = 15
示例 2:
输入:n = 4421
输出:21
解释:
各位数之积 = 4 * 4 * 2 * 1 = 32
各位数之和 = 4 + 4 + 2 + 1 = 11
结果 = 32 - 11 = 21
int subtractProductAndSum(int n) {int sum = 0, mul = 1;while (n != 0) {sum += n % 10;mul *= n % 10;n = n / 10;}return mul - sum;
}
5.丑数
丑数 就是只包含质因数 2、3 和 5 的正整数。
给你一个整数 n ,请你判断 n 是否为 丑数 。如果是,返回 true ;否则,返回 false
bool isUgly(int n) {if (n <= 0) return false;while (n % 2 == 0) {n /= 2;}while (n % 3 == 0) {n /= 3;}while (n % 5 == 0) {n /= 5;}if (n == 1)return true;elsereturn false;
}
代码优化:
bool isUgly(int n) {if (n <= 0) return false;while (n % 2 == 0) {n /= 2;}while (n % 3 == 0) {n /= 3;}while (n % 5 == 0) {n /= 5;}return n == 1;
}相关文章:

C语言 力扣习题 10.19日 day1
1.两整数相加 给你两个整数 num1 和 num2,返回这两个整数的和。 示例 1: 输入:num1 12, num2 5 输出:17 解释:num1 是 12,num2 是 5 ,它们的和是 12 5 17 ,因此返回 17 。 示例 …...

【Linux升级之路】8_Linux多线程
目录 一、【Linux初阶】多线程1 | 页表的索引作用,线程基础(优缺点、异常、用途),线程VS进程,线程控制,C多线程引入二、【Linux初阶】多线程2 | 分离线程,线程库,线程互斥࿰…...

FFT64点傅里叶变换verilog蝶形运算,代码和视频
名称:FFT64点verilog傅里叶变换 软件:Quartus 语言:Verilog 代码功能: 使用verilog代码实现64点FFT变换,使用蝶形运算实现傅里叶变换 演示视频:http://www.hdlcode.com/index.php?mhome&cView&…...

学习JS闭包
作用域 作用域分为:全局作用域和函数作用域。链式作用域:子对象会一级一级往上查找父对象的变量。 什么是闭包? 闭包可以理解为定义在函数内部的函数,是由一个函数以及与其相关的引用环境组合而成的实体。可以在函数内部访问外部函数的变量&a…...

在Mac上安装配置svn
版本控制系统对于程序员来说是至关重要的工具,而Subversion(简称svn)就是一种流行的版本控制系统。本文将指导你在Mac上安装并配置svn,让你更好地管理代码版本。 安装svn 首先,我们需要从Subversion官方网站下载适合…...
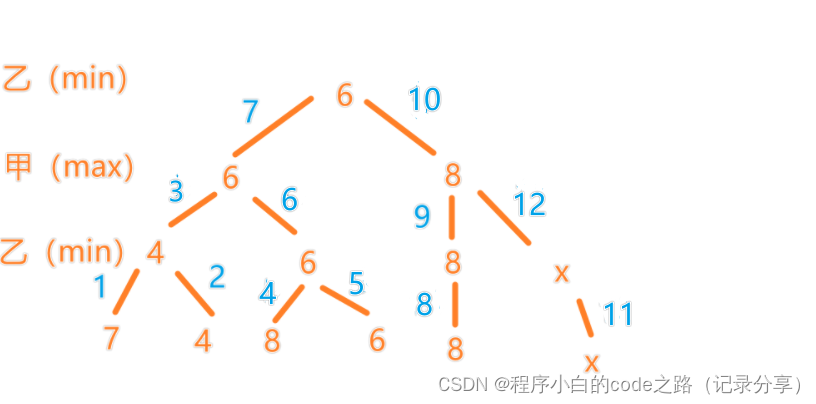
数据结构----算法--五大基本算法(这里没有写分支限界法)和银行家算法
数据结构----算法–五大基本算法(这里没有写分支限界法)和银行家算法 一.贪心算法 1.什么是贪心算法 在有多个选择的时候不考虑长远的情况,只考虑眼前的这一步,在眼前这一步选择当前的最好的方案 二.分治法 1.分治的概念 分…...
【七:docken+jenkens部署】
一:腾讯云轻量服务器docker部署Jenkins https://blog.csdn.net/qq_35402057/article/details/123589493 步骤1:查询jenkins版本:docker search jenkins步骤2:拉取jenkins镜像 docker pull jenkins/jenkins:lts步骤3:…...
智能水印相机微信小程序源码
相信大家日常在生活中或者工作中都有使用过水印相机来拍照记录吧,但是又要在手机上面多下载一个APP。 那么小编今天给大家带来一款智能水印相机,拍照自动添加时间、地点、经纬度等水印文字,可用于工作考勤、学习打卡、工作取证等,…...

一、2023 CISSP认证介绍
目录 1.CISSP概况 2.CISSP考题分析 3.备考建议 1.CISSP概况 参考:...

redis 实现互相关注功能
突然想到平时的设计软件如何实现互相关注这个功能,然后查询后大致思路如下: 可以使用 Redis 数据库来存储关注关系。 在社交网络应用程序中,互相关注功能(也称为双向关注或好友关系)是一种常见的功能,允许…...

【代码随想录】算法训练营 第十一天 第五章 栈与队列 Part 2
20. 有效的括号 题目 给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。每个右括号都有一…...

mysql 启动报错 Can t change dir to xxx, No such file or directory 配置错误或挂载导致
省流: 挂载的话,使用 /etc/fstab 放fstab里会在程序启动前加载NFS文件系统,放rc.local里往往造成程序启动加载时找不到路径。 正文: 在企业中,服务器重启,有时候会遇到mysql 启动报错 Cant change dir …...

AWS SAA-C03考试知识点整理
S3: 不用于数据库功能 分类: S3 Standard :以便频繁访问 S3 Standard-IA 或 S3 One Zone-IA : 不经常访问的数据 Glacier: 最低的成本归档数据 S3 Intelligent-Tiering智能分层 :存储具有不断变化或未知访问…...
HugeGraph 部署和Hubble1.0.0的数据导入Bug修复
背景 HugeGraph 安装部署了最新版本1.0.0,发现它的 Web 工具 Hubble 有一个大 Bug。数据导入的时候,配置节点属性映射这个选项时,下拉框只有一个选项,但实际上,元数据配置中的属性有3个,这个 Bug 是怎么产…...
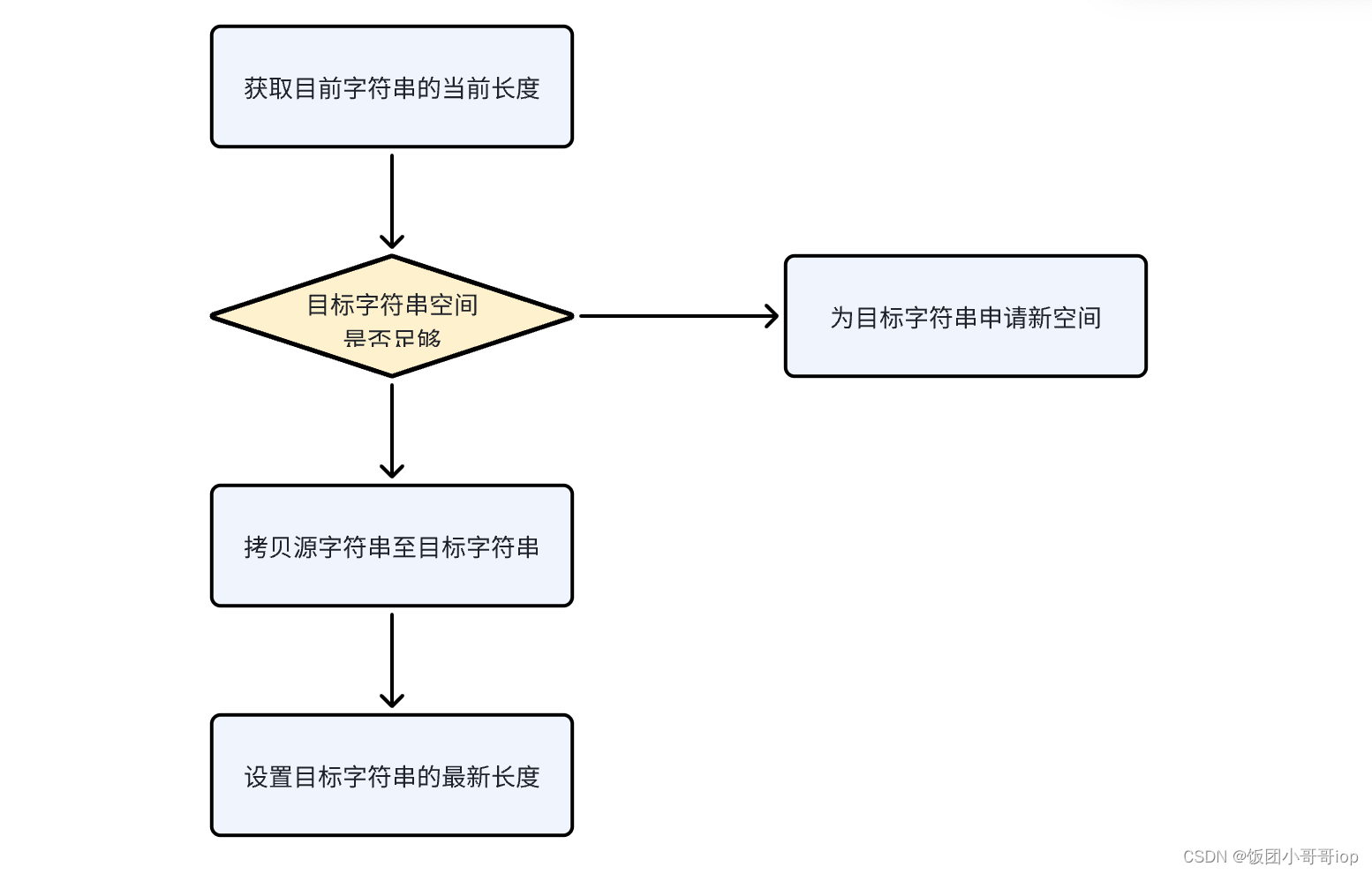
01、字符传实现为什么是SDS而不是char*?
问题: 1. sds 是什么 ? 2. sds 相对于char * 有什么好处 ?解决了哪些疑难杂症? 3. sds 有什么不足?可以优化的点? 思考下: 平常工作开发中,我们记录一条用户信息、订单信息&…...

顺应趋势,用大数据精准营销抓住大数据时代的机遇
想先问大家一个问题:“你觉得现在的营销好做吗?”想必大多数人在说到自己如何营销这一点上,都有道不完的“苦水”。“现在找客户难,投了几十万的广告费,真正来的客户却少得可怜,平均获客成本高得吓人”一位…...

面向石油和天然气的计算机视觉和深度学习1
面向石油和天然气的计算机视觉和深度学习1 1. 好处1.1 安全1.2 生产优化与估算(Production Optimization and Estimation)1.3 降低生产和维护成本(Reduce Production and Maintenance Costs) 2. 应用2.1 维护2.1.1 预测维护&#…...

微信小程序三种授权登录以及授权登录流程讲解
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《微信小程序开发实战》。🎯Ἲ…...
笔记——程序结构)
C现代方法(第10章)笔记——程序结构
文章目录 第10章 程序结构10.1 局部变量10.1.1 静态局部变量10.1.2 形式参数 10.2 外部变量10.2.1 示例:用外部变量实现栈10.2.2 外部变量的利与弊 10.3 程序块10.4 作用域10.5 构建C程序10.5.1 复杂程序:给一手牌分类 问与答写在最后 第10章 程序结构 …...

解密Web安全:Session、Cookie和Token的不解之谜
解密Web安全:Session、Cookie和Token的不解之谜 前言第一部分:什么是Session、Cookie和Token1. Session(会话):2. Cookie(HTTP Cookie):3. Token(令牌):比较: 第二部分&a…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
