leetcode_2316 统计无向图中无法互相到达点对数
1. 题意
给定一个无向图, 统计无法互相到达的点对数。
统计无法互相到达点对数
2. 题解
其实还是求联通块,求联通块可以使用搜索进行标记。还要求得联通块中元素的大小。
联通块其实也就是不相交集合,也可以用并查集来做。
每求得一个联通块的元素个数,与之前所有联通块元素个数相乘;
所以本题目两种做法:
- 搜索 + 前缀和
- 并查集 + 前缀和
2.1 并查集
并查集的介绍
- 不记录元素个数的
class Solution {public:
class UnionFind {public:explicit UnionFind(int sz):cnt(sz),pa(sz){iota(pa.begin(), pa.end(), 0);}int Find(int k ){return k == pa[k] ? k : pa[k] = Find(pa[k]);}void Union(int k1, int k2 ){int p0 = Find(k1);int p1 = Find(k2);if ( p0 != p1) {pa[p0] = p1;cnt--;}}int Cnt(){return cnt;}private:vector<int> pa;int cnt;
};long long countPairs(int n, vector<vector<int>>& edges) {UnionFind uf(n);int sz = edges.size();for (int i = 0; i < sz; ++i)uf.Union(edges[i][0], edges[i][1]);unordered_map<int, int> um;for (int i = 0; i < n; ++i ) {um[uf.Find(i)]++;}vector<int> node;for (auto &[k, v]: um) {node.push_back(v);}long long ans = 0;int pre = 0;for (int i = 0; i < node.size(); ++i)ans += 1L * pre * node[i], pre += node[i]; cout << ans << endl;return ans;}
};
- 记录元素个数的
class Solution {public:
class UnionFind {public:explicit UnionFind(int _sz):cnt(_sz),pa(_sz),sz(_sz, 1){iota(pa.begin(), pa.end(), 0);}int Find(int k ){return k == pa[k] ? k : pa[k] = Find(pa[k]);}void Union(int k1, int k2 ){int p0 = Find(k1);int p1 = Find(k2);if (p0 == p1)return ;if (sz[p0] < sz[p1] ) {pa[p0] = p1;sz[p1] += sz[p0];}else {pa[p1] = p0;sz[p0] += sz[p1];}}int Cnt(){return cnt;}int Size(int idx){ return sz[idx]; }private:vector<int> pa,sz;int cnt;
};long long countPairs(int n, vector<vector<int>>& edges) {UnionFind uf(n);int sz = edges.size();for (int i = 0; i < sz; ++i)uf.Union(edges[i][0], edges[i][1]);vector<int> node;for (int i = 0; i < n; ++i) {if (uf.Find(i) == i)node.push_back(uf.Size(i));}long long ans = 0;int pre = 0;for (int i = 0; i < node.size(); ++i)ans += 1L * pre * node[i], pre += node[i]; return ans;}
};
2.2 搜索
- DFS
class Solution {public:void dfs( int i, int &num, vector<vector<int>> &g, vector<bool> &vis) {++num;vis[i] = true;for (int &v: g[i]) {if (!vis[v]) {dfs(v, num, g, vis);}}}long long countPairs(int n, vector<vector<int>>& edges) {vector<vector<int>> g(n, vector<int>());vector<bool> vis(n, false);for (auto &v:edges){int f = v[0];int t = v[1];g[f].push_back(t);g[t].push_back(f);}long long ans = 0;long long pre = 0;for (int i = 0; i < n; ++i ) {if (!vis[i]) {int num = 0;dfs( i, num, g, vis);ans += 1l * pre * num;pre += num; }}return ans;}
};
- BFS
class Solution {public:void bfs( int i, int &num, vector<vector<int>> &g, vector<bool> &vis) {queue<int> nq;nq.push(i);++num;vis[i] = true;while( !nq.empty() ) {int idx = nq.front();nq.pop();for (auto &v:g[idx]) {if (!vis[v]) {nq.push(v);++num;vis[v] = true;}}}}long long countPairs(int n, vector<vector<int>>& edges) {vector<vector<int>> g(n, vector<int>());vector<bool> vis(n, false);for (auto &v:edges){int f = v[0];int t = v[1];g[f].push_back(t);g[t].push_back(f);}long long ans = 0;long long pre = 0;for (int i = 0; i < n; ++i ) {if (!vis[i]) {int num = 0;bfs( i, num, g, vis);cout << num << endl;ans += 1l * pre * num;pre += num; }}return ans;}
};
相关文章:

leetcode_2316 统计无向图中无法互相到达点对数
1. 题意 给定一个无向图, 统计无法互相到达的点对数。 统计无法互相到达点对数 2. 题解 其实还是求联通块,求联通块可以使用搜索进行标记。还要求得联通块中元素的大小。 联通块其实也就是不相交集合,也可以用并查集来做。 每求得一个联…...
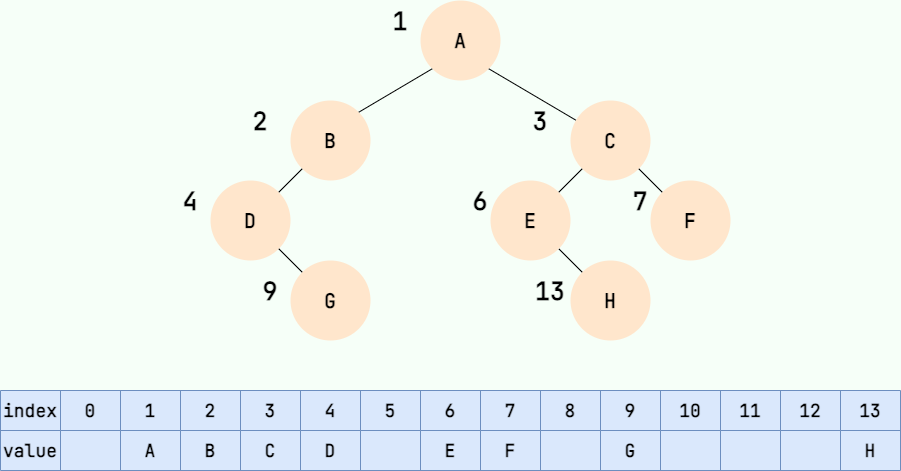
数据结构知识点总结
一、常见的数据结构 数组,栈,队列,链表,散列表,二叉树,堆,跳表,图,树。 1. 数组: 数组的元素在内存中存储是连续存放的,占有连续的存储单元&am…...

【经济研究】数字技术创新与中国企业高质量发展—来自企业数字专利的证据
数据简介:在当前数字经济时代,数字技术创新已成为驱动中国经济发展的核心要素,中国经济由高速增长转向高质量发展的“新常态”发展阶段,开启了革新经济增长方式,优化产业结构,寻找新的经济增长动能关键期。…...

Windows运维相关经验技巧
常用工具 在线PS Photoshop在线 FAQ 电脑能上网,浏览器上不了网 # 错误原因: 设置了网络代理,浏览器无法通过网络代理上网# 解决办法 关闭网络代理 (1)wini,打开设置 (2)网络和I…...
AYIT嵌入式实验室2023级C语言训练1-4章训练题
文章目录 前言1. 判断闰年2.(ab-c)*d的计算问题3.计算三角形的周长和面积4.牛牛的等差数列5.判断字母6.网购7. 牛牛的通勤8.获得月份天数9.大小写转换10.KiKi说祝福语11.小乐乐求和12.奇偶统计13.KiKi求质数个数14.乘法表15.牛牛学数列16.牛牛学数列217.数位之和18.魔法数字变换…...
trino tpcds测试
先下载tpcds-kit(有Linux和macOS),根据其文档生成数据和查询的sql。 然后hive-testbench,在ddl-tpcds/text/alltables.sql中有建表语句(用hive建表)。 建完表后LOAD DATA local INPATH "/Users/ding…...

SpringCloud学习笔记(上):服务注册与发现:Eureka、Zookeeper、Consul+负载均衡服务调用:Ribbon
壹、零基础 一、微服务架构零基础理论入门 SpringCloud分布式微服务架构的一站式解决方案,是多种微服务架构落地技术的集合体,俗称微服务全家桶。 二、从2.2.x和H版开始说起 springboot版本选择: git源码地址:https://github.…...
测算)
JavaPTA练习题 7-3 身体质量指数(BMI)测算
体重是反映和衡量一个人健康状况的重要标志之一,过胖和过瘦都不利于健康,BMI(身体质量指数)计算方法:体重(以千克为单位)除以身高(以米为单位)的平方。中国成人正常的BMI…...

类的属性和方法(java)
类和对象的使用 创建类,设计类的成员创建类的对象通过“对象.属性”或“对象.方法”调用对象的结构 代码 public class Per {public static void main(String[] args) {// TODO Auto-generated method stub//创建Person类的对象Person p1 new Person();//Scanne…...
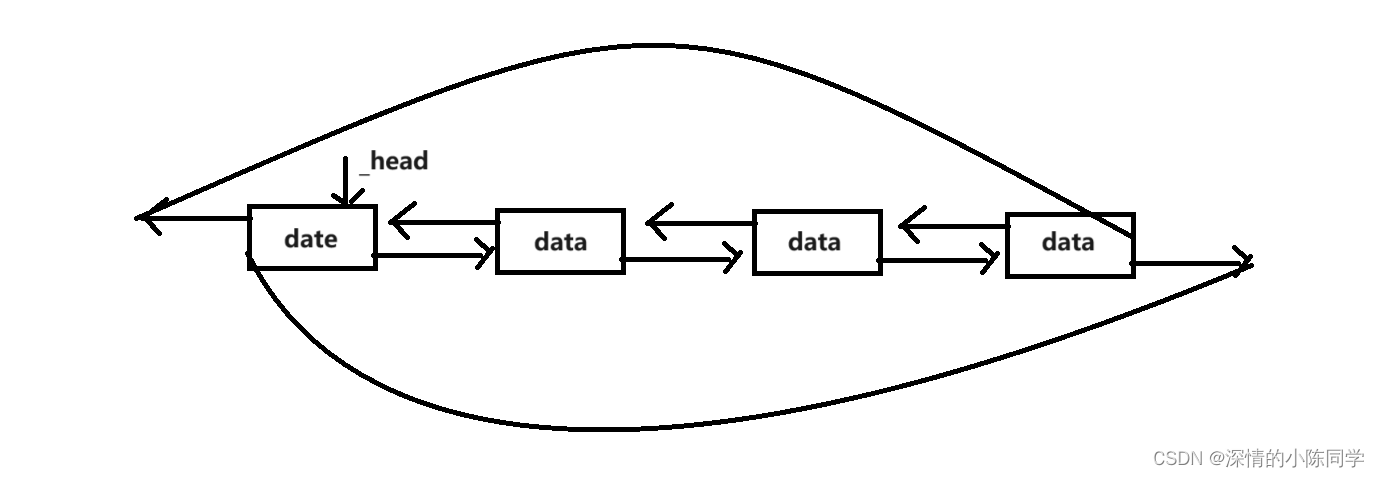
C++模拟实现——list
一、成员变量及其基本结构 1.基本结构模型 本质是一个带头双向循环列表,将节点进行封装,并且为了方便使用,进行重定义 2.节点的封装定义 template<class T>//定义节点struct list_node{list_node<T>* _prev;list_node<T>…...

FPGA的音乐彩灯VHDL流水灯LED花样,源码和视频
名称:FPGA的音乐彩灯VHDL流水灯LED 软件:Quartus 语言:VHDL 代码功能: (1)设计一彩灯控制电路,按要求控制8路(彩灯由发光 二极管代替,受实验箱限制,多路同…...
企业知识库软件,快速构建企业知识分享与团队协同的软件
企业知识库是一种特殊的在线协同文档工具,支持包括FAQ、文档、视频、知识图谱等。从本质上讲,它是基于企业知识库软件从而实现内部或外部知识的沉淀、集合、更新、共享等,能为员工或客户提供常见问题的标准回答。 今天我就基于HelpLook &…...

Java,输出一个10行的杨辉三角
据图可以发现,杨辉三角是每行的首元素和末元素都为1,中间的元素都是等于它上面的元素加上左上角的元素。 首先,先完成二数组的创建和初始化,第一行的长度为一,第二行的长度为二……以此类推。所以,外元素的…...

Java版Http请求post和get两种调用实现
在实际项目中常涉及到相互调用,对于http接口的调用,需要经过建立连接,拼接参数,调用等步骤,记录下来,方便查看。 第一步、引入jar包 pom中引入apache的httpclient包 <dependency><groupId>c…...

yjs demo: 多人在线协作画板
基于 yjs 实现实时在线多人协作的绘画功能 支持多客户端实时共享编辑自动同步,离线支持自动合并,自动冲突处理 1. 客户端代码(基于Vue3) 实现绘画功能 <template><div style"{width: 100vw; height: 100vh; over…...
虹科分享 | 赋能物流机器人:CANopen通信如何发挥重要作用?
现代物流领域迅速融入了技术进步,特别是随着自主机器人的兴起,这一趋势越发明显。确保这些机器人在复杂的仓库环境中精确运行的一个关键方面是CANopen通信协议。该协议集成了各种组件(电机、传感器、摄像头和先进的电池系统)&…...
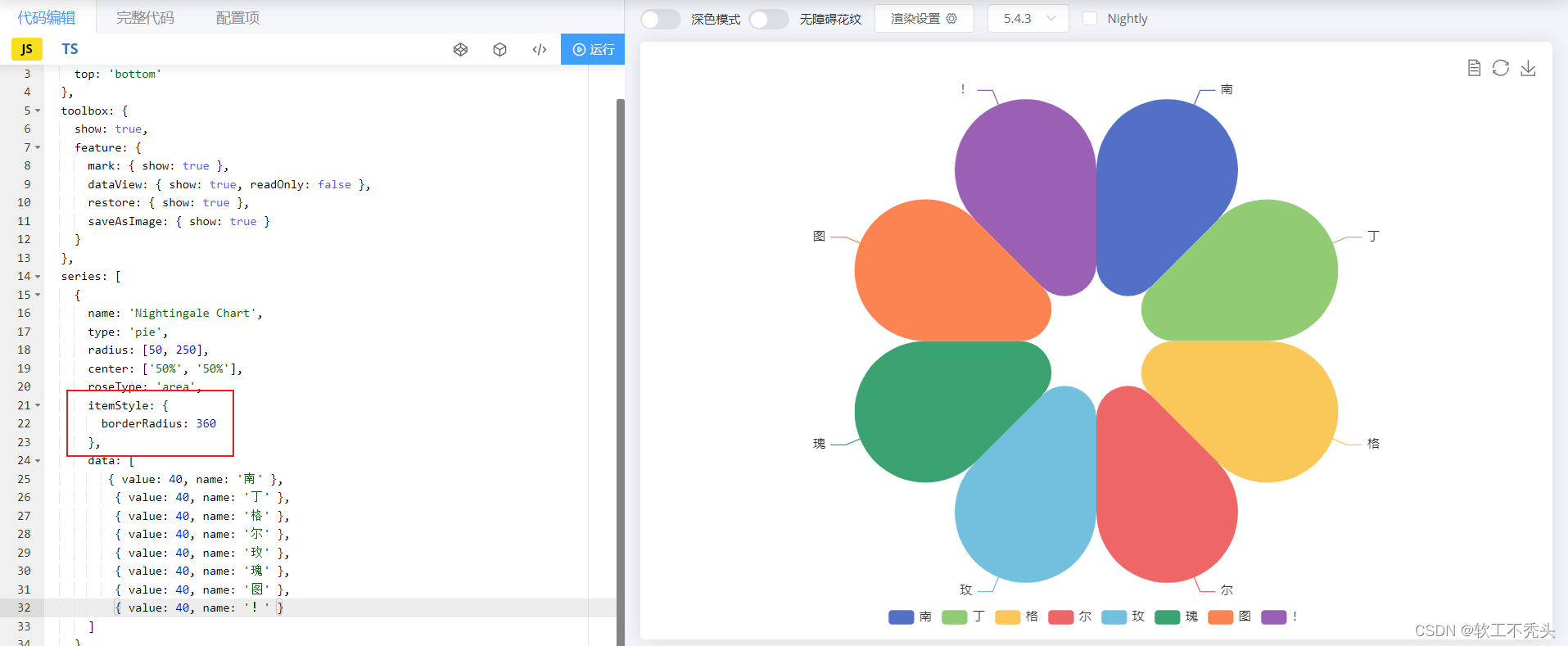
南丁格尔玫瑰图
目录 由来 效果图 echarts官网找相似图 将南丁格尔玫瑰图引进html页面中 引入echarts 准备容器 初始化echarts实例对象 指定配置项和数据(官网给的option) 将配置项给echarts 自定义南格丁尔玫瑰图 修改颜色 修改玫瑰图大小 修改图的模式为半…...

vue 大文件切片下载
前提是你上传的时候也是切片上传,下载的时候后端给你返回的是一个文件id的数组,如果是你就可以用下面的方法 // 循环下载文件 // id是每个文件的id type 是一个类型,我传入是应为给不同的组件赋值getFile(id, type) {// 通过wen文件id去获取…...
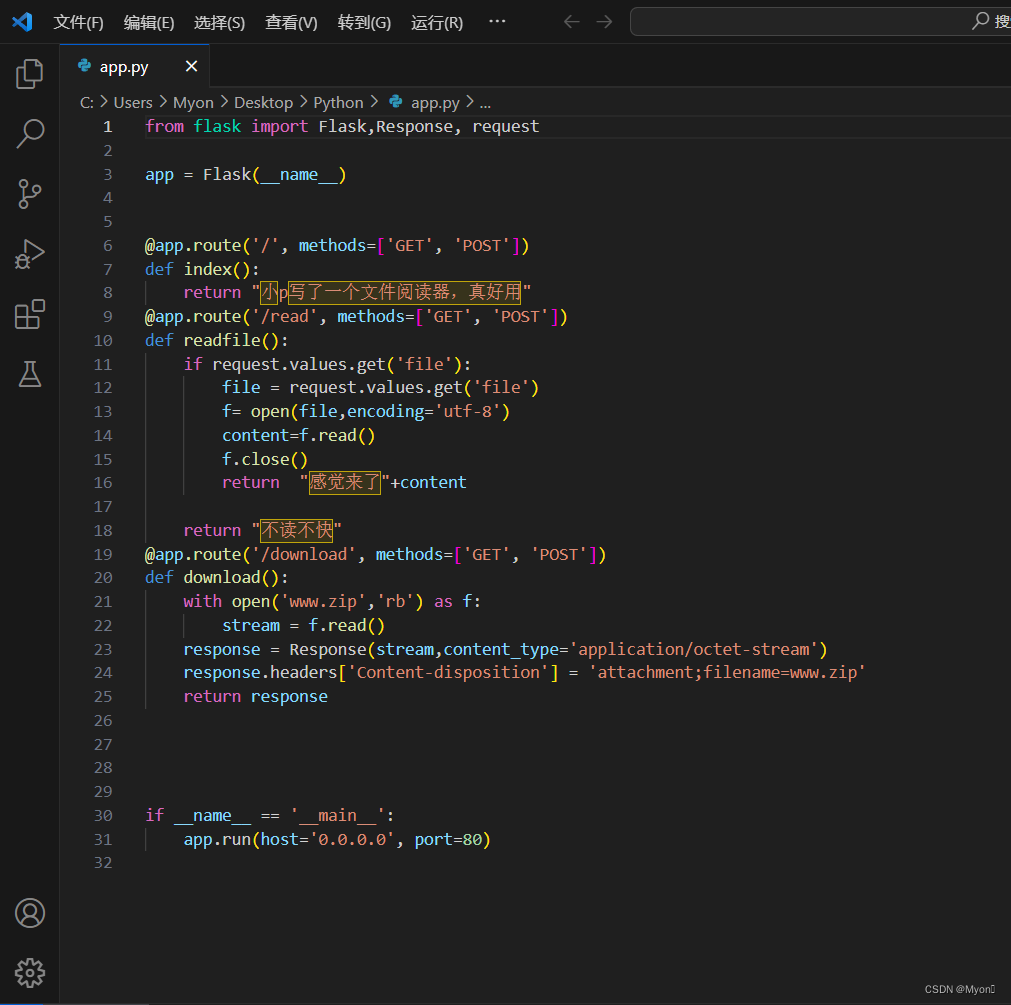
2023年“绿盟杯”四川省大学生信息安全技术大赛
pyfile 先check源码,没什么发现,接着进行目录扫描,扫到路径 /download 下载备份文件得到 www.zip,解压得到app.py 大致审一下代码: 在read目录下给file传参进行请求,如果这个东西存在就会读取出来 这里…...

YOLOv8改进实战 | 更换主干网络Backbone(二)之轻量化模型GhostnetV2
前言 轻量化网络设计是一种针对移动设备等资源受限环境的深度学习模型设计方法。下面是一些常见的轻量化网络设计方法: 网络剪枝:移除神经网络中冗余的连接和参数,以达到模型压缩和加速的目的。分组卷积:将卷积操作分解为若干个较小的卷积操作,并将它们分别作用于输入的不…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...
