151、【动态规划】leetcode ——2. 01背包问题:二维数组+一维数组(C++版本)
题目描述
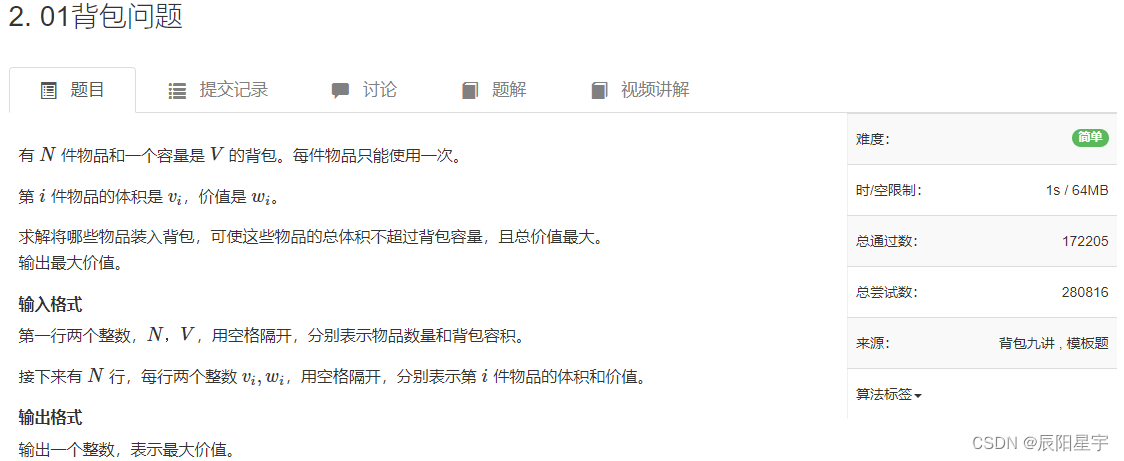
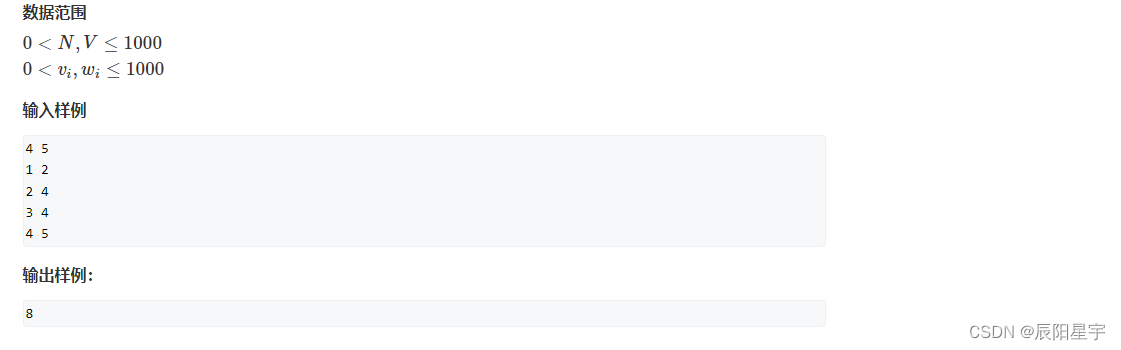
原题链接:2. 01背包问题
解题思路
(1)二维dp数组
动态规划五步曲:
(1)dp[i][j]的含义: 容量为j时,从物品1-物品i中取物品,可达到的最大价值
(2)递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]),其中dp[i - 1][j]表示不放物品i时的最大价值;j - v[i]表示给物品i留出空间,dp[i - 1][j - v[i]]表示给物品i留出空间后,放入其余物品可达到的最大价值(由于是按物品递增顺序遍历,因此为从1-i-1的物品),dp[i - 1][j - v[i]] + w[i]表示放入物品i和其余放入其余物品,可到达的最大价值。
(3)dp数组初始化: dp[0][j] = d[i][0] = 0, dp[0][j]中j >= v[i]的取w[i]
(4)遍历顺序: 从小到大,先背包后物品,或先物品后背包都可以。
(5)举例: (省略)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1010;
int dp[N][N];int main(){int n, m;int v[N], w[N];cin >> n >> m;for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {// 当前物品重量大于背包容量时,不放该物品if(j < v[i]) dp[i][j] = dp[i - 1][j];// 当前物品重量小于等于背包容量时,在放该物品后和不放该物品之间选择一个最大价值else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);}}cout << dp[n][m] << endl;return 0;
}
(2)优化为一维dp数组(滚动数组)
滚动数组含义:本轮所计算的数,需要用到上一轮的结果,依次类推,滚动计算。
优化成一维那就要在遍历上实现与二维相同的逻辑顺序,从而实现仅用一维就可以代替二维。
动态规划五步曲:
(1)dp[j]数组的含义: 容量为j时,装入的物品可达到的最大价值。
(2)递推公式: dp[j] = max(dp[j], dp[j - v[i]])
(3)dp数组初始化: dp[0] = 0
(4)遍历顺序: 两层for循环,先遍历物品,再遍历背包,内层按背包从大到小递减顺序遍历。
如果删除dp中的维度[i]后,还保持对j的从小到大遍历,那么此时的代码其实是等价于dp[i][j] = max(dp[i][j - 1], dp[i][j - v[i]),在一遍后续遍历中,因为j是从小到大与v[i]相减,在后续相减时,可能会出现本轮遍历中用过的数,会使之前使用过的数重复相加。
而如果以对j进行从大到小遍历,因为此时是j是从m到v[i],以此顺序计算dp[j - v[i]]时,在一遍后续遍历中,都是会基于上一轮对i的遍历而进行判定,并且由于j变化而v[i]不变,在后续不会出现使用过的数重复相加。每次遍历到的j所对应dp[j - v[i]]都还没有被更新,就相当于是之前的状态dp[i - 1][j - v[i]],从而得到dp[j] = dp[j - v[i]]就等价于dp[i][j] = dp[i - 1][j - v[i]]。
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1010;
int dp[N];int main(){int n, m;int v[N], w[N];cin >> n >> m;for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i++) {// 从后向前遍历,表示装入一个物品后,剩余的可装入容量达到的最大价值for(int j = m; j >= v[i]; j--) {dp[j] = max(dp[j], dp[j - v[i]] + w[i]);}}cout << dp[m] << endl;return 0;
}
参考文章:AcWing 2. 01背包问题(状态转移方程讲解) 、AcWing 2. 01背包问题 、动态规划:关于01背包问题,你该了解这些!(滚动数组)
相关文章:

151、【动态规划】leetcode ——2. 01背包问题:二维数组+一维数组(C++版本)
题目描述 原题链接:2. 01背包问题 解题思路 (1)二维dp数组 动态规划五步曲: (1)dp[i][j]的含义: 容量为j时,从物品1-物品i中取物品,可达到的最大价值 (2…...

2023-02-09 - 3 Elasticsearch基础操作
本章主要介绍ES的基础操作,具体包括索引、映射和文档的相关操作。其中,在文档操作中将分别介绍单条操作和批量操作。在生产实践中经常会通过程序对文档进行操作,因此在介绍文档操作时会分别介绍DSL请求形式和Java的高级REST编码形式。 1 索引…...
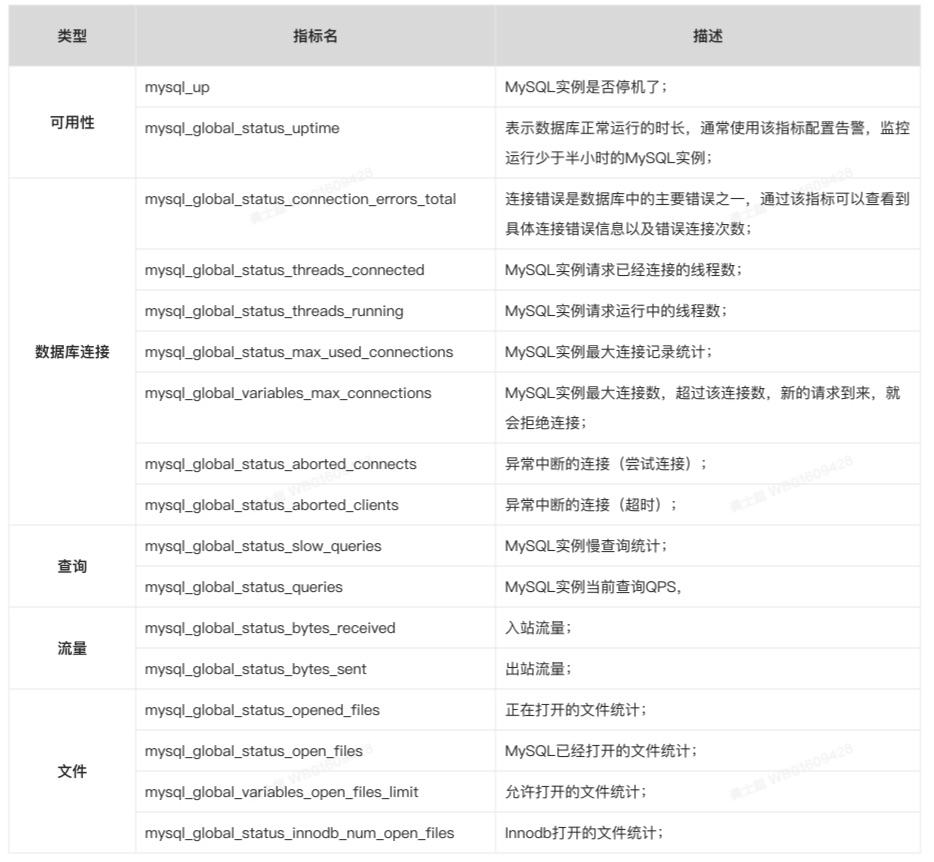
云原生系列之使用 prometheus监控MySQL实战
文章目录前言一. 实验环境二. 安装MySQL5.72.1 配置yum源2.2 安装MySQL之前的环境检查2.3 开始使用yum安装2.4 启动MySQL并测试三. 安装MySQL_exporter3.1 MySQL_exporter的介绍3.2 mysql_exporter的安装3.3 设置MySQL账户,用于数据收集3.4 启动mysql_exporter3.5 配…...
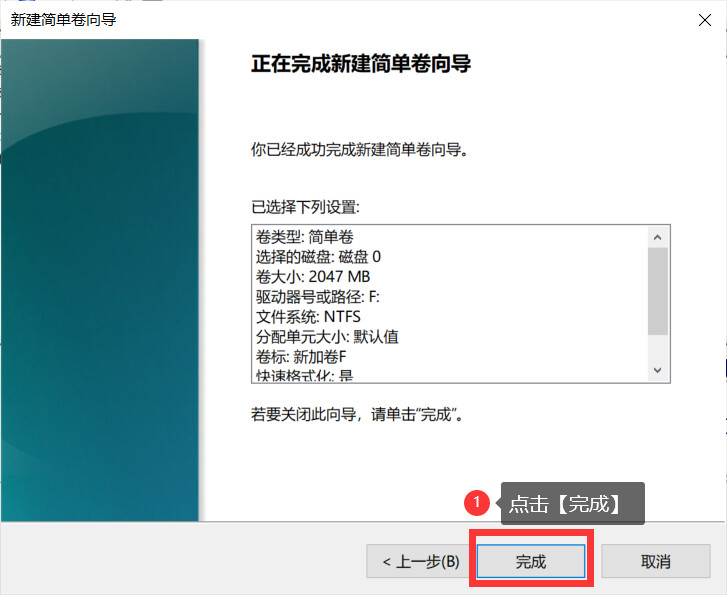
电脑分盘怎么分?分盘详细教程来了,图文教学
电脑作为小伙伴日常生活使用的工具,很多事情都需要使用电脑来进行处理。虽然小伙伴使用电脑比较多,但是还是有不少的小伙伴不知道电脑分盘怎么分?其实电脑分盘很简单,下面小编就以图文教学的方式,详细的向小伙伴介绍电…...
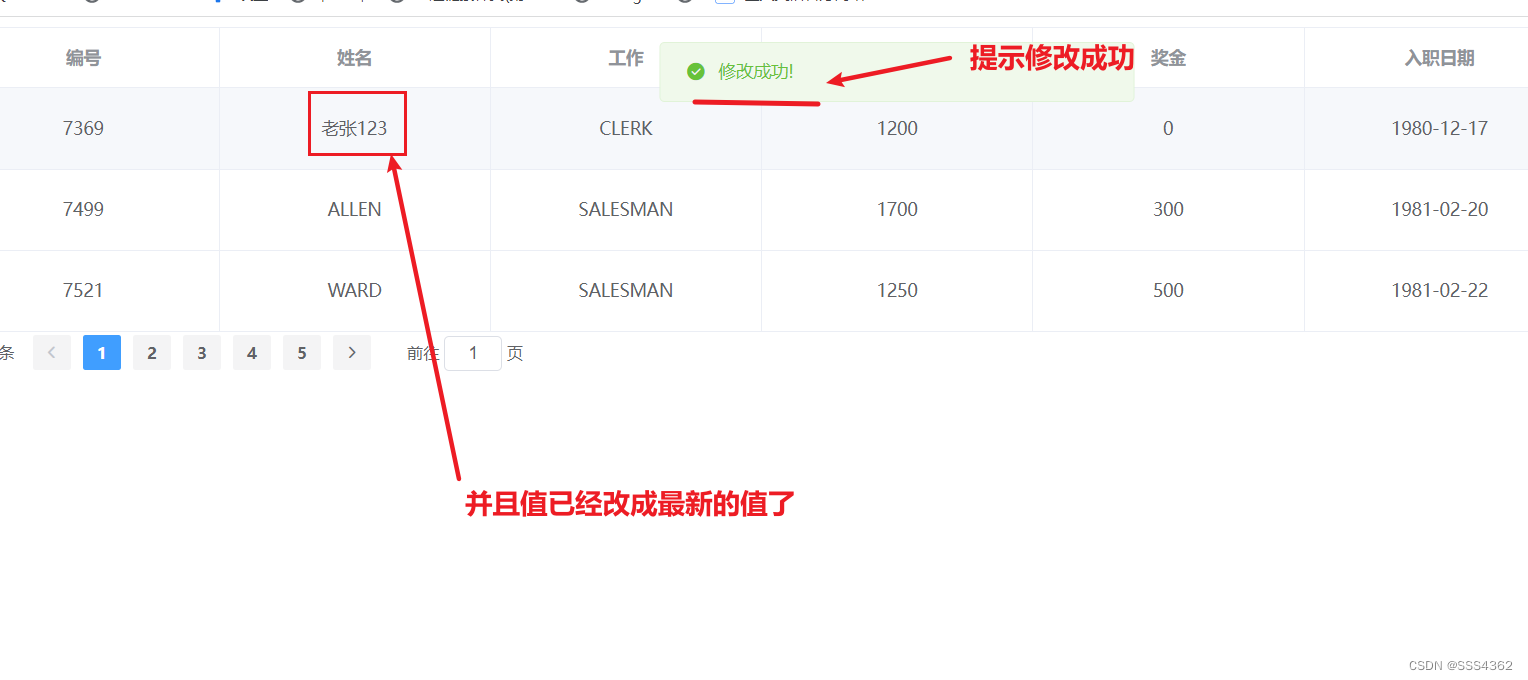
Element UI框架学习篇(四)
Element UI框架学习篇(四) 1 准备工作 1.0 创建Emp表并插入相应数据的sql语句 /*MySQL数据库*/SET NAMES utf8mb4; SET FOREIGN_KEY_CHECKS 0;-- ---------------------------- -- Table structure for emp -- ---------------------------- DROP TABLE IF EXISTS emp; CRE…...
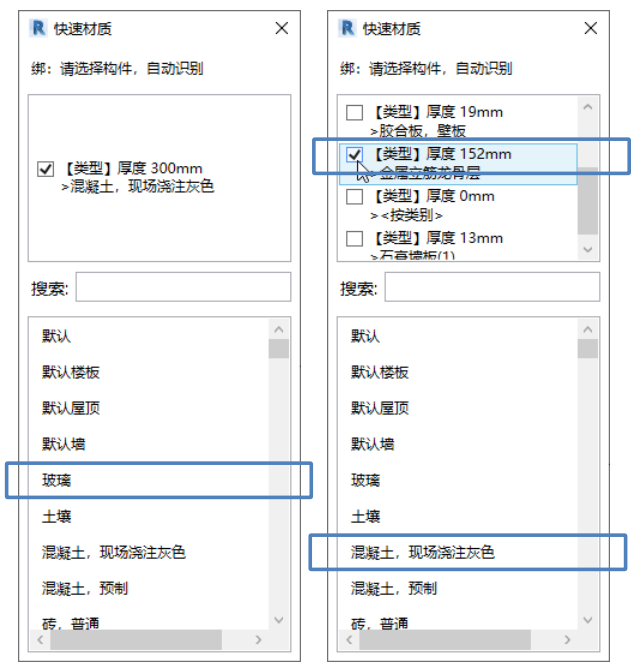
Revit快速材质切换:同一墙面赋予不同材质的方法
一、Revit中对同一墙面赋予不同材质的方法 方法1:零件法 重点:通过工作平面面板上的设置工作平面命令选取正确的面取消勾选通过原始分类的材质,如图1所示 方法2:拆分构造层绘制一道墙体,选择创建的墙体,单击…...
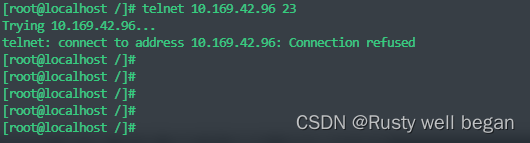
【Linux operation 56】Linux 系统验证端口连通性
linux 系统验证端口连通性 1、前提 Linux系统有时候需要测试某个端口的连通性,然而ping命令只能测试某个IP通不通,不能测试某端口的连通性。 因为ping命令是基于ICMP协议,是计算机网络中的网络层的协议,但是想要测试某个的连通…...
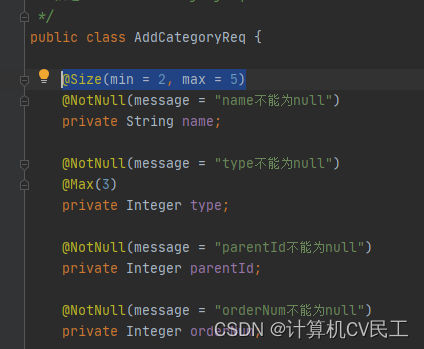
@Valid注解配合属性校验注解完成参数校验并且优化异常处理
Valid注解配合属性校验注解完成参数校验并且优化参数校验异常处理1 Valid注解配合属性校验注解完成参数校验2 优化参数校验异常处理1 Valid注解配合属性校验注解完成参数校验 向数据库商品分类表中新增商品分类字段,并校验传入的参数 不使用注解的传统方法…...

每天一道大厂SQL题【Day08】
每天一道大厂SQL题【Day08】 大家好,我是Maynor。相信大家和我一样,都有一个大厂梦,作为一名资深大数据选手,深知SQL重要性,接下来我准备用100天时间,基于大数据岗面试中的经典SQL题,以每日1题…...

朗润国际期货:2023/2/10今日期市热点及未来焦点
2023/2/10今日期市热点及未来焦点 1月份人 民币贷款增加4.9万亿元 创历史新高 中国央行: 1月份人民币贷款增加4.9万亿元,同比多增9227亿元。分部门看,住户贷款增加2572亿元,其中,短期贷款增加341亿元,中长期贷款增加…...
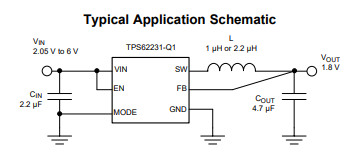
TLV73312PQDRVRQ1稳压器TPS622314TDRYRQ1应用原理图
一、TLV73312PQDRVRQ1低压差稳压器 1.2V 300MATLV733 300mA 低压差稳压器是有 300mA 拉电流能力的超小型、低静态电流 LDO,具有良好的线路和负载瞬态性能。这些器件具有 1% 的典型精度。TLV733 系列设计具有先进的无电容器结构,确保无需输入或输出电容器…...

课程回顾|以智能之力,加速媒体生产全自动进程
本文内容整理自「智能媒体生产」系列课程第二讲:视频AI与智能生产制作,由阿里云智能视频云高级技术专家分享视频AI原理,AI辅助媒体生产,音视频智能化能力和底层原理,以及如何利用阿里云现有资源使用音视频AI能力。课程…...
)
C库函数文件操作(fopen、fread、fwrite、fclose)
C库函数 C文件操作用库函数实现,包含在stdio.h中,系统自动打开和关闭三个标准文件: 标准输入-键盘(stdin)标准输出-显示器(stdout)标准出错输出-显示器(stderr) 文件打…...

【Java|golang】1798. 你能构造出连续值的最大数目
给你一个长度为 n 的整数数组 coins ,它代表你拥有的 n 个硬币。第 i 个硬币的值为 coins[i] 。如果你从这些硬币中选出一部分硬币,它们的和为 x ,那么称,你可以 构造 出 x 。 请返回从 0 开始(包括 0 )&a…...

VB 消息、消息队列、事件
windows是图像化界面,多任务消息windows系统将消息(大的结构)发给其他应用程序Windows消息包含了所有的外部输入或者计算机内部信息,应用程序的消息队列先进先出,Windows消息的循环--每个应用程序里有自己的消息循环外…...

Linux实用指令记录
du Linux du(英文全拼:disk usage)命令用于显示目录或文件的大小。du 会显示指定的目录或文件所占用的磁盘空间。用例:当前路径/home/hzf/Voice/wespeaker-master$ du -h -d 1 371G ./examples 52K ./tools 280K ./run…...
Jetpack Compose中的绘制流程和自定义布局
Jetpack Compose中绘制流程的三个阶段 与大多数其他界面工具包一样,Compose 会通过几个不同的“阶段”来渲染帧。如果我们观察一下 Android View 系统,就会发现它有 3 个主要阶段:测量、布局和绘制。Compose 和它非常相似,但开头…...

笔试题-2023-芯动-数字IC设计【纯净题目版】
回到首页:2023 数字IC设计秋招复盘——数十家公司笔试题、面试实录 推荐内容:数字IC设计学习比较实用的资料推荐 题目背景 笔试时间:2022.07.23应聘岗位:数字IC设计笔试时长:120min笔试平台:nowcoder牛客网题目类型:单选题(10道)、不定项选择(5道)、填空(5道)、问…...

高压放大器在孔道灌浆非线性超声测试中的应用
实验名称:高压放大器在孔道灌浆非线性超声测试中的应用研究方向:无损检测测试目的:超声波作为频率高于20kHz的声波被广泛应用于各类结构的无损检测中,以超声波作为探伤波的无损检测法称为超声波无损检测法,简称超声波法…...

vue3响应式原理
通过Proxy(代理): 拦截对data任意属性的进行操作, 包括属性值的增删改查 通过 Reflect(反射): 动态对被代理对象的相应属性进行特定的操作 通过采用两者结合使用的方式实现响应式 Proxy 对象用于创建一个对象的代理,从而实现基本操作的拦截和自定义(如…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
