模拟退火算法(SA)求解旅行商问题(TSP)python
目录
一、模拟退火算法求解TSP(city14)的python代码
二、city14的运行结果
三、 模拟退火算法求解TSP(city30)的python代码
四、city30的运行结果
一、模拟退火算法求解TSP(city14)的python代码
import random
import numpy as np
import math
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False'''计算路径总路程的函数'''
def fitness(n,X,Y,X0):''':param n: 城市数量:param X: n个城市的横坐标:param Y: n个城市的纵坐标:param X0: 一个解向量:return: 总路程'''s=0for i in range(n):if i!=n-1:s=s+np.sqrt((X[X0[i]]-X[X0[i+1]])**2+(Y[X0[i]]-Y[X0[i+1]])**2)else:s=s+np.sqrt((X[X0[i]]-X[X0[0]])**2+(Y[X0[i]]-Y[X0[0]])**2)return s'''定义领域搜索运算操作——交换操作'''
def exchange(X0,q):''':param X0: 一个解向量:param q: 指定的需要交换的数的两个位置的列表,列表长度为2:return: 一个领域解'''X1=X0.copy()temp=X1[q[0]]X1[q[0]]=X1[q[1]]X1[q[1]]=tempreturn X1'''定义随机产生初始解的函数'''
def initialX0(n):''':param n: 城市数量:return: 一个初始解'''X0=random.sample(range(n),n)return X0'''模拟退火算法——TSP'''
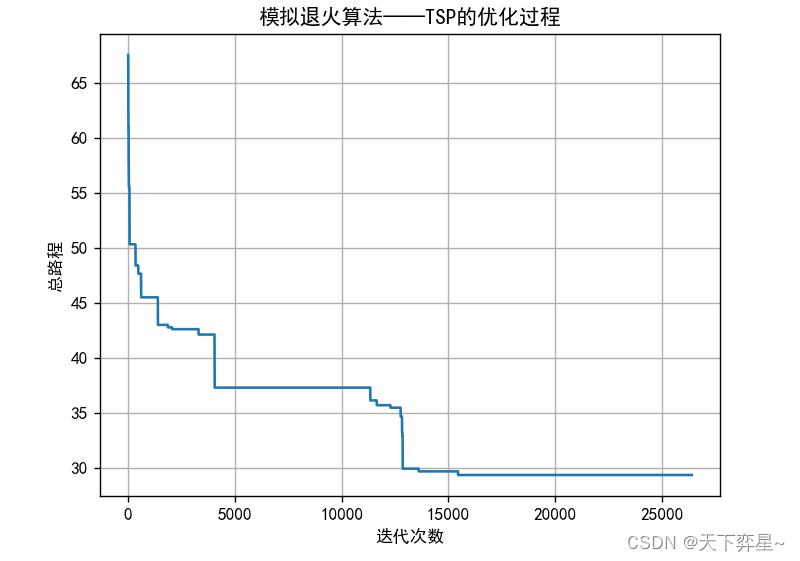
def SA_TSP(n,X,Y,n_TK,r,T_f):''':param n: 城市数量:param X: n个城市的横坐标:param Y: n个城市的纵坐标:param n_TK: 内循环的迭代次数:param T_down: 降温变化:param T_f: 终止温度:return: 最优路径和最短距离''''''产生一个初始解'''X0=initialX0(n)print("初始解:\n{}".format(X0))print("初始解的总路程:\n{}".format(fitness(n,X,Y,X0)))'''初始温度'''T0=1000'''存储历史最优路径'''X_min=[]X_min.append(X0)'''存储历史最优距离'''s_min=[]s_min.append(fitness(n,X,Y,X0))k=0while T0>T_f:for i in range(n_TK):#随机产生两个位置q=random.sample(range(n),2)#领域运算得到一个随机领域解X1=exchange(X0,q)#计算初始解和随机领域解的目标函数值s1=fitness(n,X,Y,X0)s2=fitness(n,X,Y,X1)#更新历史最优解if s2<min(s_min):s_min.append(s2)X_min.append(X1)else:s_min.append(s_min[-1])X_min.append(X_min[-1])'''判断是否更新解'''if s2<s1:X0=X1else:E=math.exp(-(s2-s1)/T0)R=random.uniform(0,1)if E>R:X0=X1k=k+1'''降温'''T0=T0*r'''绘制优化过程'''plt.plot(range(k+1),s_min)plt.grid()plt.title("模拟退火算法——TSP的优化过程")plt.xlabel("迭代次数")plt.ylabel("总路程")plt.show()'''绘制路线图'''#最优路径W=X_min[-1]for i in range(n):if i!=n-1:plt.plot([X[W[i]],X[W[i+1]]],[Y[W[i]],Y[W[i+1]]],c='plum')else:plt.plot([X[W[i]],X[W[0]]],[Y[W[i]],Y[W[0]]],c='plum')plt.scatter(X,Y,c='red')plt.title("路线图")plt.xlabel("x")plt.ylabel("y")plt.show()return X_min[-1],s_min[-1]'''主函数'''
if __name__=="__main__":'''城市的数量'''n=14'''定义14个城市的坐标'''city_x=[16.47,16.47,20.09,22.39,25.23,22.00,20.47,17.20,16.30,14.05,16.53,21.52,19.41,20.09]city_y=[96.10,94.44,92.54,93.37,97.24,96.05,97.02,96.29,97.38,98.12,97.38,95.59,97.13,92.55]'''内循环的迭代次数'''n_Tk=200'''降温变化'''r=0.9'''终止温度'''T_f=0.001'''模拟退火算法求解TSP'''Xmin,smin=SA_TSP(n,city_x,city_y,n_Tk,r,T_f)print("最优路径:\n{}".format(Xmin))print("最短距离:\n{}".format(smin))二、city14的运行结果


三、 模拟退火算法求解TSP(city30)的python代码
import random
import numpy as np
import math
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False'''计算路径总路程的函数'''
def fitness(n,X,Y,X0):''':param n: 城市数量:param X: n个城市的横坐标:param Y: n个城市的纵坐标:param X0: 一个解向量:return: 总路程'''s=0for i in range(n):if i!=n-1:s=s+np.sqrt((X[X0[i]]-X[X0[i+1]])**2+(Y[X0[i]]-Y[X0[i+1]])**2)else:s=s+np.sqrt((X[X0[i]]-X[X0[0]])**2+(Y[X0[i]]-Y[X0[0]])**2)return s'''定义领域搜索运算操作——交换操作'''
def exchange(X0,q):''':param X0: 一个解向量:param q: 指定的需要交换的数的两个位置的列表,列表长度为2:return: 一个领域解'''X1=X0.copy()temp=X1[q[0]]X1[q[0]]=X1[q[1]]X1[q[1]]=tempreturn X1'''定义随机产生初始解的函数'''
def initialX0(n):''':param n: 城市数量:return: 一个初始解'''X0=random.sample(range(n),n)return X0'''模拟退火算法——TSP'''
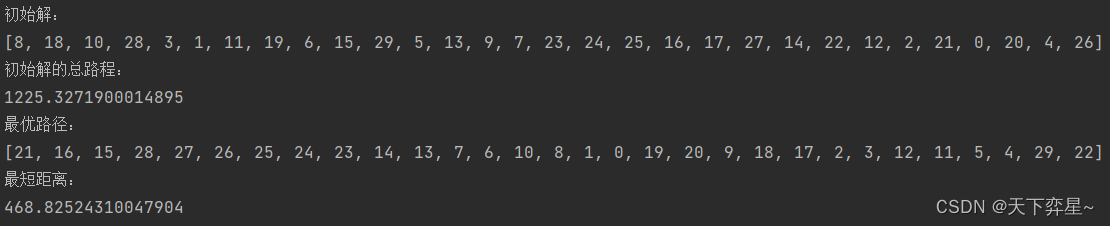
def SA_TSP(n,X,Y,n_TK,r,T_f):''':param n: 城市数量:param X: n个城市的横坐标:param Y: n个城市的纵坐标:param n_TK: 内循环的迭代次数:param T_down: 降温变化:param T_f: 终止温度:return: 最优路径和最短距离''''''产生一个初始解'''X0=initialX0(n)print("初始解:\n{}".format(X0))print("初始解的总路程:\n{}".format(fitness(n,X,Y,X0)))'''初始温度'''T0=2000'''存储历史最优路径'''X_min=[]X_min.append(X0)'''存储历史最优距离'''s_min=[]s_min.append(fitness(n,X,Y,X0))k=0while T0>T_f:for i in range(n_TK):#随机产生两个位置q=random.sample(range(n),2)#领域运算得到一个随机领域解X1=exchange(X0,q)#计算初始解和随机领域解的目标函数值s1=fitness(n,X,Y,X0)s2=fitness(n,X,Y,X1)#更新历史最优解if s2<min(s_min):s_min.append(s2)X_min.append(X1)else:s_min.append(s_min[-1])X_min.append(X_min[-1])'''判断是否更新解'''if s2<s1:X0=X1else:E=math.exp(-(s2-s1)/T0)R=random.uniform(0,1)if E>R:X0=X1k=k+1'''降温'''T0=T0*r'''绘制优化过程'''plt.plot(range(k+1),s_min)plt.grid()plt.title("模拟退火算法——TSP的优化过程")plt.xlabel("迭代次数")plt.ylabel("总路程")plt.show()'''绘制路线图'''#最优路径W=X_min[-1]for i in range(n):if i!=n-1:plt.plot([X[W[i]],X[W[i+1]]],[Y[W[i]],Y[W[i+1]]],c='plum')else:plt.plot([X[W[i]],X[W[0]]],[Y[W[i]],Y[W[0]]],c='plum')plt.scatter(X,Y,c='red')plt.title("路线图")plt.xlabel("x")plt.ylabel("y")plt.show()return X_min[-1],s_min[-1]'''主函数'''
if __name__=="__main__":'''城市的数量'''n=30'''定义30个城市的坐标'''city_x=[41, 37, 54, 25, 7, 2, 68, 71, 54, 83, 64, 18, 22, 83, 91, 25, 24, 58, 71, 74, 87,18, 13, 82, 62, 58, 45,41,44, 4]city_y=[94, 84, 67, 62, 64, 99, 58, 44, 62, 69, 60, 54, 60, 46, 38, 38, 42, 69, 71, 78, 76,40, 40, 7, 32, 35, 21,26,35, 50]'''内循环的迭代次数'''n_Tk=300'''降温变化'''r=0.9'''终止温度'''T_f=0.001'''模拟退火算法求解TSP'''Xmin,smin=SA_TSP(n,city_x,city_y,n_Tk,r,T_f)print("最优路径:\n{}".format(Xmin))print("最短距离:\n{}".format(smin))四、city30的运行结果


相关文章:

模拟退火算法(SA)求解旅行商问题(TSP)python
目录 一、模拟退火算法求解TSP(city14)的python代码 二、city14的运行结果 三、 模拟退火算法求解TSP(city30)的python代码 四、city30的运行结果 一、模拟退火算法求解TSP(city14)的python代码 impor…...
Intelijj使用Gitee团队开发
初始化项目到Gitee服务器 成功标识: 添加团队成员 点击管理——仓库成员设置——开发者 2.添加仓库成员 (最多不超过5人) 3.通过链接或者二维码邀请新成员,或者可以自己手动添加新成员并提交 多人项目仓库创建完成 通…...

气象台使用vr模拟仿真实训教学降低成本投入
气候仿真实验室用于模拟高低温、高湿、干燥、阳光光照、降雨、降雪、覆冰、雾天与强风等多种环境适应性试验等气候和环境条件,在环境试验中,温度、湿度、光照、降雨这些常见的仿真环境都很容易实现。而比较少见的雾天、强风、降雪等环境就比较难。因此为…...
智能井盖是什么?万宾科技智能井盖传感器有什么特点
智能井盖是一种基于物联网和人工智能技术的新型城市设施。它不仅具备传统井盖的功能,还能通过数字化、自动化的方式实现远程监控和智能管理,提升城市运行效率和服务水平。 WITBEE万宾智能井盖传感器EN100-C2是一款井盖异动监测的传感终端。对窨井盖状态(…...

使用 类加载器 或者 类对象 读取文件
相对路径:项目 的 根目录 开始查找。( 但是在我们真正开发的时候,我们读到的更多的文件并不是直接放在我们项目里面这个文件夹里面,而是放在我们模块里面 )同理可得,我们直接创建 文件 b.txt 会在项目的根目…...

《深度学习推荐系统》王喆 笔记
这个笔记,是我记录的阅读该书,对我比较有用的一些点。不算是能完全覆盖全书知识点的笔记。 能完全覆盖全书知识点,比较详尽的笔记,可以参考如下。 《深度学习推荐系统》超级详细读书笔记https://www.zhihu.com/tardis/bd/art/44…...
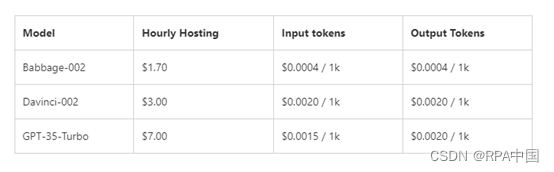
微软Azure OpenAI支持数据微调啦!可打造专属ChatGPT
10月17日,微软在官网宣布,现在可以在Azure OpenAI公共预览版中对GPT-3.5-Turbo、Babbage-002 和Davinci-002模型进行数据微调。 使得开发人员通过自己的数据集,便能打造独一无二的ChatGPT。例如,通过海量医疗数据进行微调&#x…...

Kali Linux 安装搭建 hadoop 平台 详细教程
1)前期环境准备:(虚拟机、jdk、ssh) 2)SSH相关配置 安装SSH Server服务器:apt-get install openssh-server 更改默认的SSH密钥 cd /etc/ssh mkdir ssh_key_backup mv ssh_host_* ssh_key_backup 创建新…...

leetcode做题笔记190. 颠倒二进制位
颠倒给定的 32 位无符号整数的二进制位。 提示: 请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因…...

JAVA如何获取服务器ip
一、最简单的方法就是使用InetAddress获取本机ip InetAddress.getLocalHost().getHostAddress(); public static void main(String[] args) {try {//用 getLocalHost() 方法创建的InetAddress的对象InetAddress address InetAddress.getLocalHost();System.out.println(addr…...
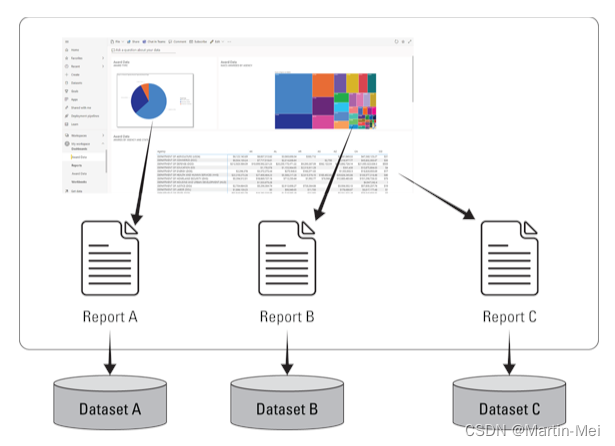
Power BI 傻瓜入门 4. Power BI:亮点
本章内容包含: 在Power BI Desktop上学习诀窍摄入数据使用模型试用Power BI服务 就像评估一个由多种成分组成的蛋糕一样,Power BI要求其用户熟悉商业智能(BI)解决方案中的功能。几乎所有与Power BI交互的用户都是从桌面版开始的…...
)
网络参考资料搬运(3)
(1) Python: 使用Python打开新的终端(terminal)并执行语句 通过Python 打开各系统(MAC, LINUX, WINDOWS)下的终端 (Terminal) python执行shell脚本的几种方法 自己写Linux命令 用Python写个Linux系统命令 Python 使用sftp传输文件…...

Bias in Emotion Recognition with ChatGPT
本文是LLM系列文章,针对《Bias in Emotion Recognition with ChatGPT》的翻译。 chatGPT在情绪识别中的偏差 摘要1 引言2 方法3 结果4 讨论5 结论 摘要 本技术报告探讨了ChatGPT从文本中识别情绪的能力,这可以作为交互式聊天机器人、数据注释和心理健康…...
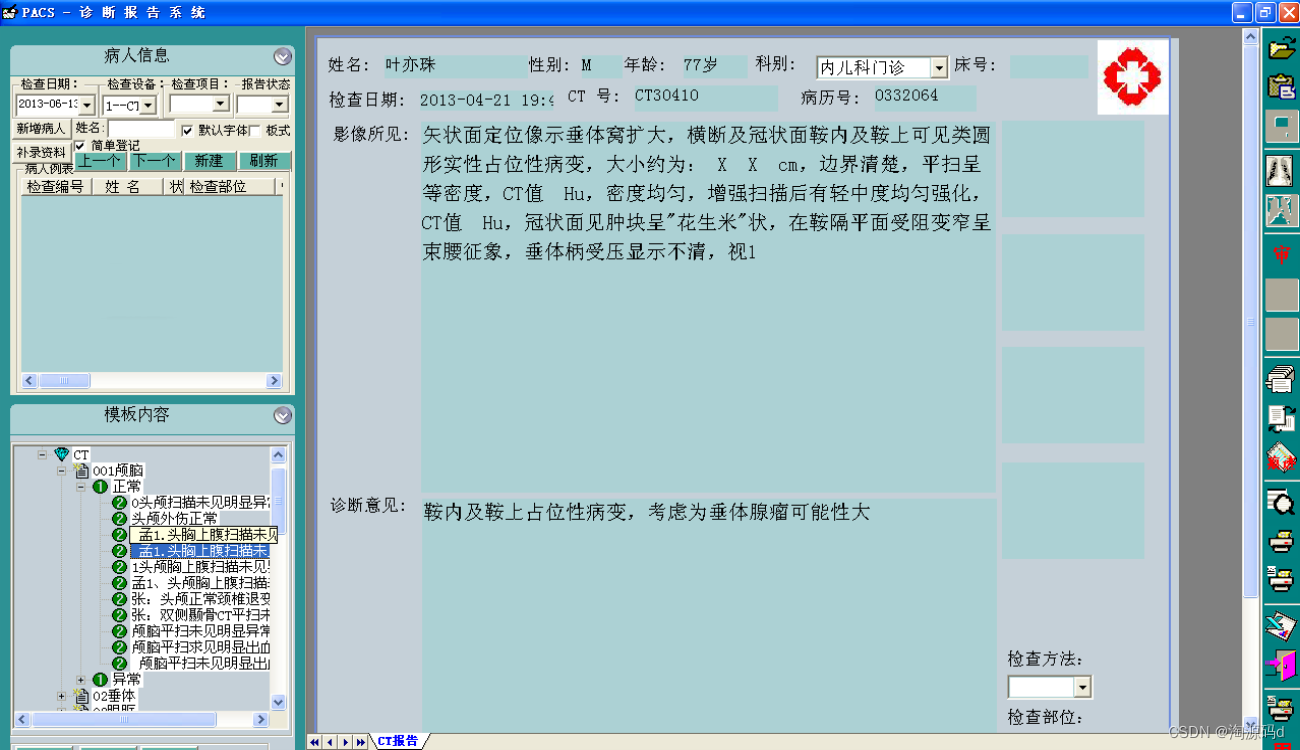
【PACS系统源码】与医院HIS系统双向数据交换,实现医学影像集成与影像后处理功能
医院医学影像PACS系统源码,集成三维影像后处理功能,包括三维多平面重建、三维容积重建、三维表面重建、三维虚拟内窥镜、最大/小密度投影、心脏动脉钙化分析等功能。系统功能强大,代码完整。 PACS系统与医院HIS实现双向数据交换,…...

深度学习中常用的激活函数有sigmoid、tanh、ReLU、LeakyReLU、PReLU、GELU等。
深度学习中常用的激活函数 1. Sigmoid函数2. Tanh函数3. ReLU函数4. LeakyReLU函数5. PReLU函数6. ELU函数:7. GELU函数: 深度学习中常用的激活函数有sigmoid、tanh、ReLU、LeakyReLU、PReLU等。 1. Sigmoid函数 Sigmoid函数公式为 f ( x ) 1 1 e −…...

mysql同时使用order by排序和limit分页数据重复问题
目录 场景再现: 解决方案: 问题分析: mysql官方描述: 场景再现: 最近排查数据时发现使用order by及limit分页时会出现不同页数数据重复问题及有的数据分页不会显示,但是按条件搜索就可以搜索出来。 解决方案&#x…...

英语——歌诀篇——歌诀记忆法
介词用法速记歌 年月季前要用in, 日子前面却不行。 遇到几号要用on, 上午下午又用in。 要说某时上下午, 用on换in才可行。 午夜黄昏和黎明, 要用at不用in。 差儿分到几点, 写个“to”在中间。 若是几点过几分…...

打破运维疆界:异构复杂网络环境的集中监控和管理
在当今多元化的IT环境中,异构环境的管理成为了企业IT团队的一大挑战。如何在多种技术架构、多样的应用环境中实现高效的运维管理,是众多企业正在面临的问题。在本文中,我们将探讨监控易在异构环境中的运维监控表现,并通过实际案例…...

ubuntu安装debian包的命令dpkg和apt的详解
dpkg是Debian Packager的缩写 官方文档https://manpages.ubuntu.com/manpages/jammy/en/man1/dpkg.1.html ubuntu的dpkg命令类似centos的rpm命令,dpkg主要用于对已下载到本地和已安装的.deb软件包进行管理比如安装、构建、删除。dpkg不能自动下载和安装.deb软件包也…...

【暴力剪枝】CF1708D
https://codeforces.com/contest/1708/problem/D 题意 思路 这样的操作下,数列减的速度是非常快的,也就是说,易出现很多的0,0的操作没啥意义,所以我们要找到第一个 >0 的数对其后的序列进行排序,就能大…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
