深度学习中常用的激活函数有sigmoid、tanh、ReLU、LeakyReLU、PReLU、GELU等。
深度学习中常用的激活函数
- 1. Sigmoid函数
- 2. Tanh函数
- 3. ReLU函数
- 4. LeakyReLU函数
- 5. PReLU函数
- 6. ELU函数:
- 7. GELU函数:
深度学习中常用的激活函数有sigmoid、tanh、ReLU、LeakyReLU、PReLU等。
1. Sigmoid函数
Sigmoid函数公式为 f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1,它的输出值在[0,1]之间,可以用来解决二元分类问题。它的主要特点是它是可导的,并且输出值可以被解释为概率。但是,如果输入值过大或过小,会导致梯度消失问题,对于较深的神经网络来说不太适用。
PyTorch的代码示例:
import torch.nn.functional as Fclass Net(nn.Module):def __init__(self):super(Net, self).__init__()self.fc1 = nn.Linear(10, 5)self.fc2 = nn.Linear(5, 1)def forward(self, x):x = F.sigmoid(self.fc1(x))x = F.sigmoid(self.fc2(x))return x
2. Tanh函数
Tanh函数公式为 f ( x ) = e x − e − x e x + e − x f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} f(x)=ex+e−xex−e−x,它的输出值在[-1,1]之间,可以用来解决回归问题。与sigmoid不同的是,它的输出是以0为中心的,因此幂次大的输入值仍然会导致梯度消失问题。
PyTorch的代码示例:
import torch.nn.functional as Fclass Net(nn.Module):def __init__(self):super(Net, self).__init__()self.fc1 = nn.Linear(10, 5)self.fc2 = nn.Linear(5, 1)def forward(self, x):x = F.tanh(self.fc1(x))x = F.tanh(self.fc2(x))return x
3. ReLU函数
ReLU函数公式为 f ( x ) = m a x ( 0 , x ) f(x)=max(0, x) f(x)=max(0,x),它的输出值在[0,无穷)之间,可以用来解决分类和回归问题。它有以下优点:1)解决了梯度消失问题;2)计算速度快。
PyTorch的代码示例:
import torch.nn.functional as Fclass Net(nn.Module):def __init__(self):super(Net, self).__init__()self.fc1 = nn.Linear(10, 5)self.fc2 = nn.Linear(5, 1)def forward(self, x):x = F.relu(self.fc1(x))x = F.relu(self.fc2(x))return x
4. LeakyReLU函数
LeakyReLU函数公式为 f ( x ) = m a x ( 0.01 x , x ) f(x)=max(0.01x, x) f(x)=max(0.01x,x),它的输出值在(-无穷,无穷)之间,是ReLU的改进版。在输入值为负数时,它不是完全为0,而是有一个小的斜率,可以避免神经元死亡。
PyTorch的代码示例:
import torch.nn.functional as Fclass Net(nn.Module):def __init__(self):super(Net, self).__init__()self.fc1 = nn.Linear(10, 5)self.fc2 = nn.Linear(5, 1)self.LeakyReLU = nn.LeakyReLU(0.01)def forward(self, x):x = self.LeakyReLU(self.fc1(x))x = self.LeakyReLU(self.fc2(x))return x
5. PReLU函数
PReLU函数公式为:
f ( x ) = { x , if x > 0 α x , otherwise f(x) = \begin{cases} x, & \text{if $x > 0$}\\ \alpha x, & \text{otherwise} \end{cases} f(x)={x,αx,if x>0otherwise
其中 α \alpha α 是可学习的参数,它的输出值在(-无穷,无穷)之间,是LeakyReLU的改进版。与LeakyReLU不同的是, α \alpha α 不是固定的,而是可以根据训练数据自适应调节。
PyTorch的代码示例:
import torch.nn.functional as Fclass Net(nn.Module):def __init__(self):super(Net, self).__init__()self.fc1 = nn.Linear(10, 5)self.fc2 = nn.Linear(5, 1)self.PReLU = nn.PReLU()def forward(self, x):x = self.PReLU(self.fc1(x))x = self.PReLU(self.fc2(x))return x
6. ELU函数:
ELU函数的数学公式为 f ( x ) = { x , x > 0 α ( e x − 1 ) , x ≤ 0 f(x)=\begin{cases}x, & x>0\\\alpha(e^x-1), & x\leq0\end{cases} f(x)={x,α(ex−1),x>0x≤0,它是另一种解决ReLU“死亡”现象的函数,通过引入一个指数函数来平滑负数区间。
以下是使用PyTorch实现ELU函数的代码示例:
import torch.nn.functional as Fx = torch.randn(2, 3)
y = F.elu(x, alpha=1.0)
print(y)
深度学习中常用的激活函数有sigmoid、ReLU、LeakyReLU、ELU、SeLU等,其中gelu是近年来提出的一种新的激活函数。
7. GELU函数:
GELU (Gaussian Error Linear Units)函数是一种近年来提出的新型激活函数,其原理是基于高斯误差函数的近似。其作用是在保持ReLU函数优点的同时,减少其缺点。将输入的值 x x x通过高斯分布的累积分布函数(CDF) F ( x ) F(x) F(x),来获得激活函数的输出值。其数学表达式如下:
g e l u ( x ) = x ⋅ Φ ( x ) , 其中 Φ ( x ) = 1 2 [ 1 + e r f ( x 2 ) ] \mathrm{gelu}(x)=x\cdot\Phi (x), \ \mathrm{其中}\Phi(x)=\frac{1}{2}[1+\mathrm{erf}(\frac{x}{\sqrt{2}})] gelu(x)=x⋅Φ(x), 其中Φ(x)=21[1+erf(2x)]
其中, Φ ( x ) \Phi(x) Φ(x)为高斯分布的累积分布函数。
GELU函数具有以下特点:
- 可微性:GELU函数可导,可以使用反向传播算法训练神经网络。
- 非线性:与ReLU函数相似,GELU函数具有非线性特点,可以学习非线性函数。
- 平滑性:GELU函数在整个实数轴上都是连续可导的,可以减少梯度消失和爆炸问题。
- 计算效率高:由于GELU函数采用了近似求解,计算速度较ReLU函数更快。
由于高斯分布的概率密度函数(PDF)在均值处最大,因此gelu在接近0的地方具有很好的非线性特性,同时也有一定的平滑性,能够一定程度上减少梯度消失问题,提高模型的泛化能力。
PyTorch代码示例:
import torch.nn as nnclass MyModel(nn.Module):def __init__(self):super(MyModel, self).__init__()self.fc = nn.Linear(10, 20)self.act = nn.GELU()def forward(self, x):x = self.fc(x)x = self.act(x)return xmodel = MyModel()
import torch
import torch.nn.functional as Fclass Net(torch.nn.Module):def __init__(self):super(Net, self).__init__()self.fc1 = torch.nn.Linear(10, 20)self.fc2 = torch.nn.Linear(20, 2)def forward(self, x):x = F.gelu(self.fc1(x))x = F.gelu(self.fc2(x))return x
在上述示例代码中,我们使用了PyTorch中的F.gelu函数,实现了GELU激活函数对网络中的每个神经元进行激活。
相关文章:

深度学习中常用的激活函数有sigmoid、tanh、ReLU、LeakyReLU、PReLU、GELU等。
深度学习中常用的激活函数 1. Sigmoid函数2. Tanh函数3. ReLU函数4. LeakyReLU函数5. PReLU函数6. ELU函数:7. GELU函数: 深度学习中常用的激活函数有sigmoid、tanh、ReLU、LeakyReLU、PReLU等。 1. Sigmoid函数 Sigmoid函数公式为 f ( x ) 1 1 e −…...

mysql同时使用order by排序和limit分页数据重复问题
目录 场景再现: 解决方案: 问题分析: mysql官方描述: 场景再现: 最近排查数据时发现使用order by及limit分页时会出现不同页数数据重复问题及有的数据分页不会显示,但是按条件搜索就可以搜索出来。 解决方案&#x…...

英语——歌诀篇——歌诀记忆法
介词用法速记歌 年月季前要用in, 日子前面却不行。 遇到几号要用on, 上午下午又用in。 要说某时上下午, 用on换in才可行。 午夜黄昏和黎明, 要用at不用in。 差儿分到几点, 写个“to”在中间。 若是几点过几分…...

打破运维疆界:异构复杂网络环境的集中监控和管理
在当今多元化的IT环境中,异构环境的管理成为了企业IT团队的一大挑战。如何在多种技术架构、多样的应用环境中实现高效的运维管理,是众多企业正在面临的问题。在本文中,我们将探讨监控易在异构环境中的运维监控表现,并通过实际案例…...

ubuntu安装debian包的命令dpkg和apt的详解
dpkg是Debian Packager的缩写 官方文档https://manpages.ubuntu.com/manpages/jammy/en/man1/dpkg.1.html ubuntu的dpkg命令类似centos的rpm命令,dpkg主要用于对已下载到本地和已安装的.deb软件包进行管理比如安装、构建、删除。dpkg不能自动下载和安装.deb软件包也…...

【暴力剪枝】CF1708D
https://codeforces.com/contest/1708/problem/D 题意 思路 这样的操作下,数列减的速度是非常快的,也就是说,易出现很多的0,0的操作没啥意义,所以我们要找到第一个 >0 的数对其后的序列进行排序,就能大…...

代码格式化的使用
前言 本文主要介绍了代码格式化,以及各个平台如何使用快捷键进行代码格式化,如有错误之处,欢迎在评论区交流讨论~ 代码格式化 代码格式化是一种编程实践,它涉及调整源代码的外观,以提高可读性和一致性。 这包括调整缩进、空格、换行符和括号等元素的使…...

【Unity地编】地形系统搭建入门详解
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:UI_…...
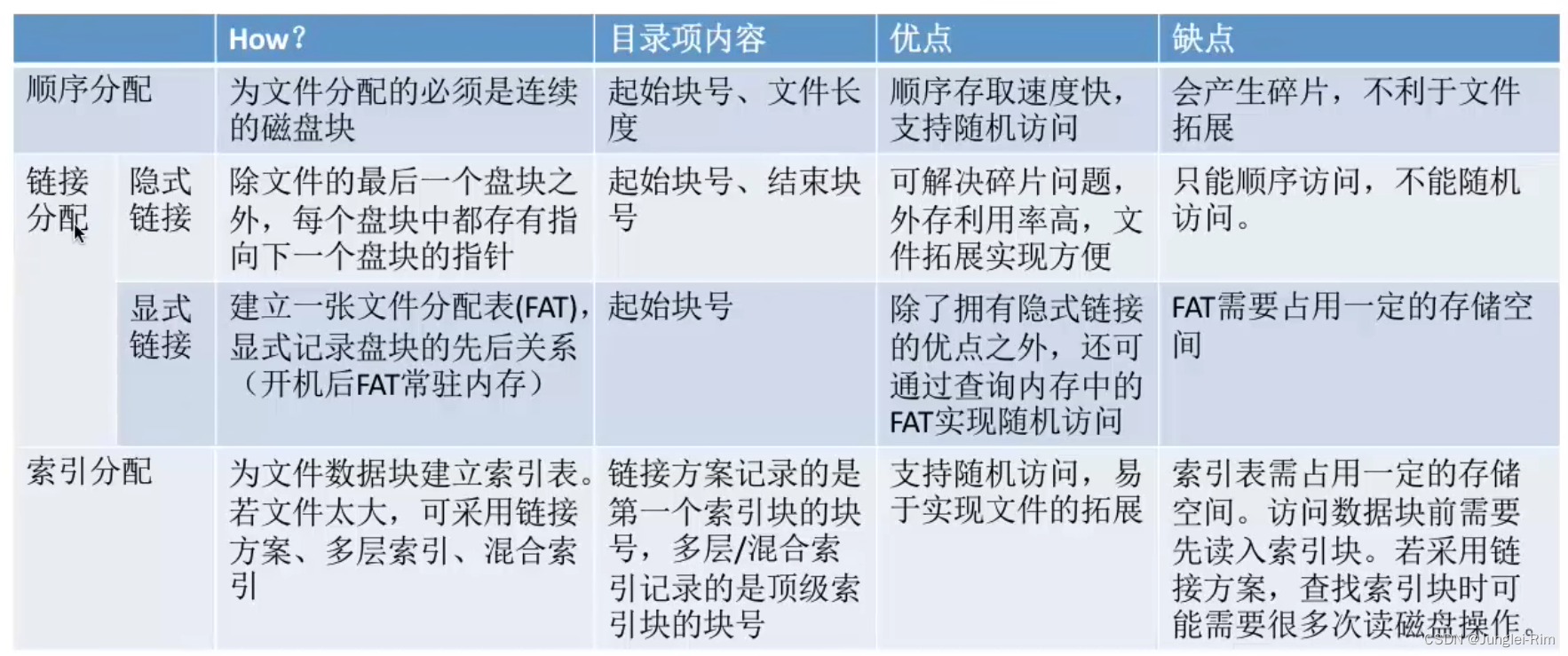
文件的物理结构(连续分配,链接分配,索引分配)
1.文件块,磁盘块 类似于内存分页,磁盘中的存储单元也会被分为一个个“块/磁盘块/物理块”。 很多操作系统中,磁盘块的大小与内存块、页面的大小相同。 内存与磁盘之间的数据交换(即读/写操作、磁盘I/O)都是以“块”为…...
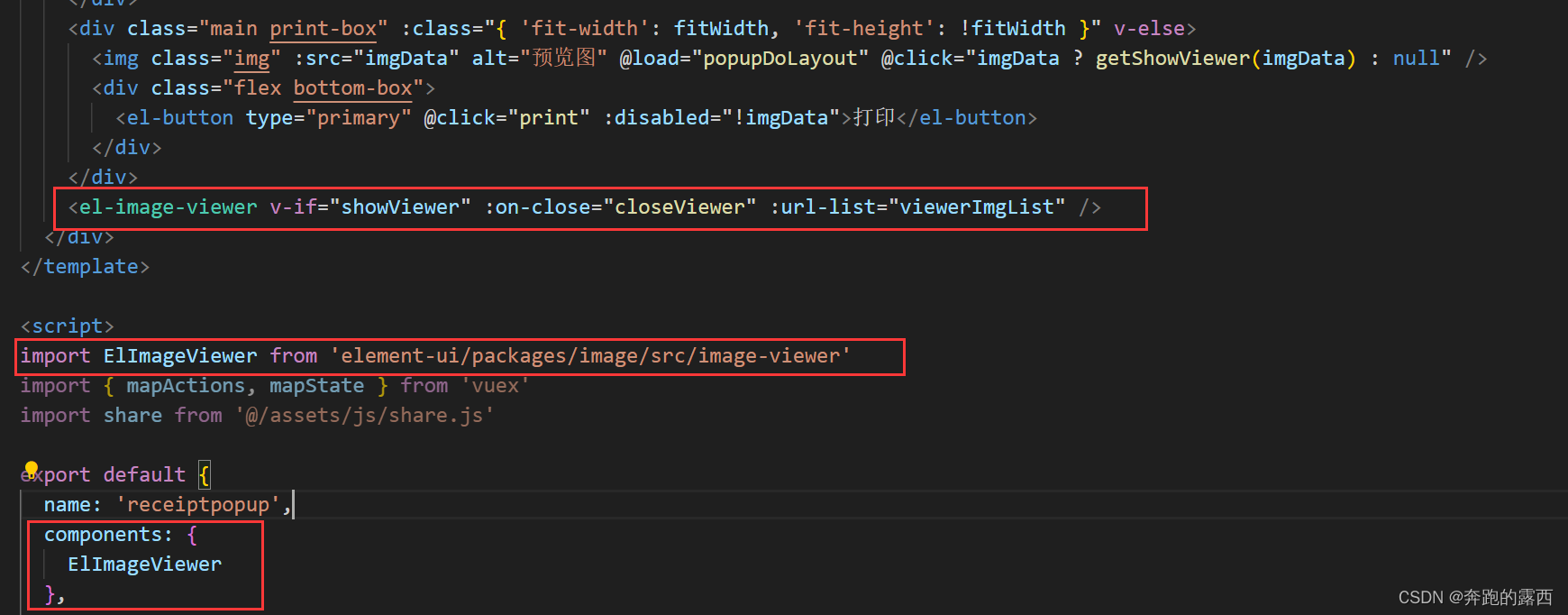
vue2 解密图片地址(url)-使用blob文件-打开png格式图片
一、背景 开发中需要对加密文件进行解码,如图片等静态资源。 根据后端给到的url地址,返回的是图片文件,但是乱码的,需要解码成png图片进行展示 二、请求接口 将后端返回的文件转为文件流,创建Blob对象来存储二进制…...

cuda PyTorch
1. GPU对应的CUDA版本 nvidia-smi CUDA Version: 12.2 GPU diver 大于cuda toolkit, pytorch 版本根据cuda toolkit 2. 查看nvcc的版本(即cuda toolkit 版本) nvcc --version Cuda compilation tools, release 12.2, V12.2.91 Build cud…...

vue视频直接播放rtsp流;vue视频延迟问题解决;webRTC占cpu太大卡死问题解决;解决webRTC播放卡花屏问题:
播放多个视频 <div class"video-box"><div class"video"><iframe style"width:100%;height:100%;" name"ddddd" id"iframes" scrolling"auto" :src"videoLeftUrl"></iframe>&l…...

leetcode_2316 统计无向图中无法互相到达点对数
1. 题意 给定一个无向图, 统计无法互相到达的点对数。 统计无法互相到达点对数 2. 题解 其实还是求联通块,求联通块可以使用搜索进行标记。还要求得联通块中元素的大小。 联通块其实也就是不相交集合,也可以用并查集来做。 每求得一个联…...
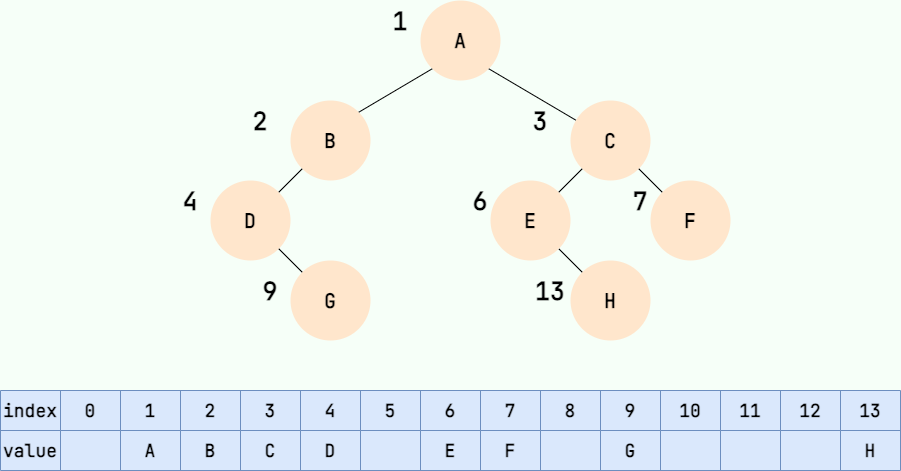
数据结构知识点总结
一、常见的数据结构 数组,栈,队列,链表,散列表,二叉树,堆,跳表,图,树。 1. 数组: 数组的元素在内存中存储是连续存放的,占有连续的存储单元&am…...

【经济研究】数字技术创新与中国企业高质量发展—来自企业数字专利的证据
数据简介:在当前数字经济时代,数字技术创新已成为驱动中国经济发展的核心要素,中国经济由高速增长转向高质量发展的“新常态”发展阶段,开启了革新经济增长方式,优化产业结构,寻找新的经济增长动能关键期。…...

Windows运维相关经验技巧
常用工具 在线PS Photoshop在线 FAQ 电脑能上网,浏览器上不了网 # 错误原因: 设置了网络代理,浏览器无法通过网络代理上网# 解决办法 关闭网络代理 (1)wini,打开设置 (2)网络和I…...
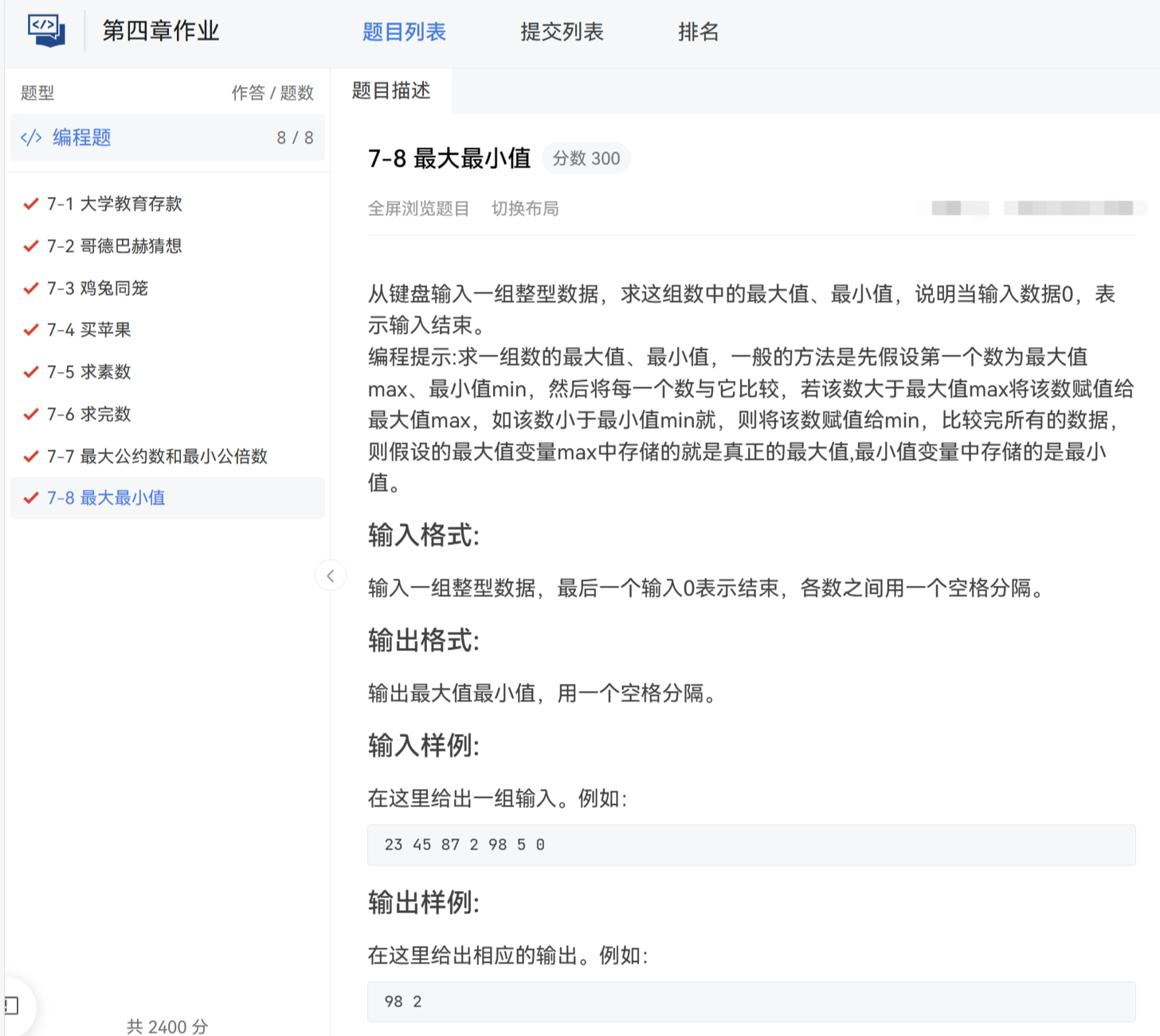
AYIT嵌入式实验室2023级C语言训练1-4章训练题
文章目录 前言1. 判断闰年2.(ab-c)*d的计算问题3.计算三角形的周长和面积4.牛牛的等差数列5.判断字母6.网购7. 牛牛的通勤8.获得月份天数9.大小写转换10.KiKi说祝福语11.小乐乐求和12.奇偶统计13.KiKi求质数个数14.乘法表15.牛牛学数列16.牛牛学数列217.数位之和18.魔法数字变换…...
trino tpcds测试
先下载tpcds-kit(有Linux和macOS),根据其文档生成数据和查询的sql。 然后hive-testbench,在ddl-tpcds/text/alltables.sql中有建表语句(用hive建表)。 建完表后LOAD DATA local INPATH "/Users/ding…...

SpringCloud学习笔记(上):服务注册与发现:Eureka、Zookeeper、Consul+负载均衡服务调用:Ribbon
壹、零基础 一、微服务架构零基础理论入门 SpringCloud分布式微服务架构的一站式解决方案,是多种微服务架构落地技术的集合体,俗称微服务全家桶。 二、从2.2.x和H版开始说起 springboot版本选择: git源码地址:https://github.…...
测算)
JavaPTA练习题 7-3 身体质量指数(BMI)测算
体重是反映和衡量一个人健康状况的重要标志之一,过胖和过瘦都不利于健康,BMI(身体质量指数)计算方法:体重(以千克为单位)除以身高(以米为单位)的平方。中国成人正常的BMI…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
