Leetcode—2530.执行K次操作后的最大分数【中等】(C语言向上取整数学公式)
2023每日刷题(五)
Leetcode—2530.执行K次操作后的最大分数

向上取整思想
参考了这篇文章

有人肯定会问,这个向上取整为什么是这样来的。接下来我简单讲解一下。
数学式: x y 数学式:\frac{x}{y} 数学式:yx有以下两种情况
- x能整除y,则 x y \frac{x}{y} yx就是向上取整和向下取整结果一致的情况,不需要额外转换。也就是说 x y \frac{x}{y} yx的向上取整和向下取整都是它本身,例如 6 3 = 2 \frac{6}{3}=2 36=2, 6 3 \frac{6}{3} 36向下取整和向上取整结果都一样,即为2
- x不能整除y,则 x y \frac{x}{y} yx是向下取整结果,不符合我们的需求。例如 5 2 = 2 \frac{5}{2}=2 25=2,但是我们需要它的向上取整的值,就不能直接用/。
解释一下 ( x + y − 1 ) / y (x + y - 1) / y (x+y−1)/y
- 如果x能整除y,那么 ( x + y − 1 ) / y (x + y - 1) / y (x+y−1)/y的结果就等价于 x / y x / y x/y,例如 6 3 = 2 \frac{6}{3}=2 36=2
- 如果x不能整除y,那么 ( x + y − 1 ) / y (x + y - 1) / y (x+y−1)/y结果就是向上取整的值。例如 x = 5 , y = 2 x=5,y=2 x=5,y=2,则 ( 5 + 2 − 1 ) / 2 = 3 (5 + 2 - 1) / 2 = 3 (5+2−1)/2=3,即为 5 2 \frac{5}{2} 25向上取整的值。
你也可以这么理解,
- 若x能整除y,例如x=2y,所以向上整除为2
- 若x不能整除y,例如x=2y+1,也可以是 [ 2 y + 1 , 3 y ) \left[2y+1, 3y\right) [2y+1,3y),所以 ( x + y − 1 ) / y = ( 2 y + 1 + y − 1 ) = 3 (x + y - 1) / y = (2y + 1 + y - 1) = 3 (x+y−1)/y=(2y+1+y−1)=3
直接法实现代码
void max(int *nums, int numsSize, int *e) {int i = 0;int max = nums[0];int cnt = 0;for(i = 1; i < numsSize; i++) {if(max < nums[i]) {max = nums[i];cnt = i;}}*e = cnt;
}long long maxKelements(int* nums, int numsSize, int k){int i = 0;long long ans = 0;int cur = 0;for(; i < k; i++) {max(nums, numsSize, &cur);ans += nums[cur];nums[cur] = (nums[cur] + 2) / 3;}return ans;
}
测试结果

因为我的时间复杂度太大了,即 O ( k n ) O(kn) O(kn),主要是也没要求时间复杂度啊。。。接下来用最大堆的方法做,也就是大根堆
最大堆实现代码
void swap(int *a, int *b) {int tmp = *a;*a = *b;*b = tmp;
}void downAdjustHeap(int* heap, int low, int high) {// 相当于双亲为i,左孩子为2*i+1,右孩子为2*i+2,因为这里数组从下标0开始int i = low, j = i * 2 + 1;while(j <= high) {if(j + 1 <= high && heap[j + 1] > heap[j]) {j = j + 1;}if(heap[j] > heap[i]) {swap(&heap[j], &heap[i]);i = j;j = j * 2 + 1;} else {break;}}
}void createHeap(int* arr, int n) {// 建立大顶堆int i;for(i = n / 2 - 1; i >= 0; i--) {downAdjustHeap(arr, i, n - 1);}
}long long maxKelements(int* nums, int numsSize, int k){// 建立大顶堆,即最大堆createHeap(nums, numsSize);long long ans = 0;int i;for(i = 0; i < k; i++) {ans += nums[0];// 向上取整nums[0] = (nums[0] + 2) / 3;downAdjustHeap(nums, 0, numsSize - 1);}return ans;
}

测试结果

之后我会持续更新,如果喜欢我的文章,请记得一键三连哦,点赞关注收藏,你的每一个赞每一份关注每一次收藏都将是我前进路上的无限动力 !!!↖(▔▽▔)↗感谢支持!
相关文章:

Leetcode—2530.执行K次操作后的最大分数【中等】(C语言向上取整数学公式)
2023每日刷题(五) Leetcode—2530.执行K次操作后的最大分数 向上取整思想 参考了这篇文章 有人肯定会问,这个向上取整为什么是这样来的。接下来我简单讲解一下。 数学式: x y 数学式:\frac{x}{y} 数学式:…...

CMakeList 编写示例
cmake_minimum_required(VERSION 3.8) #指定cmake的最小版本 set(PROJECT_NAME Untitled_1) #初始化变量 project(${PROJECT_NAME} VERSION 1.0) #创建一个project set(CMAKE_AUTOMOC ON) #初始化内置变量, 该变量为Qt工程专属变量 set(CMAKE_AUTORCC ON) set(CMAKE_A…...
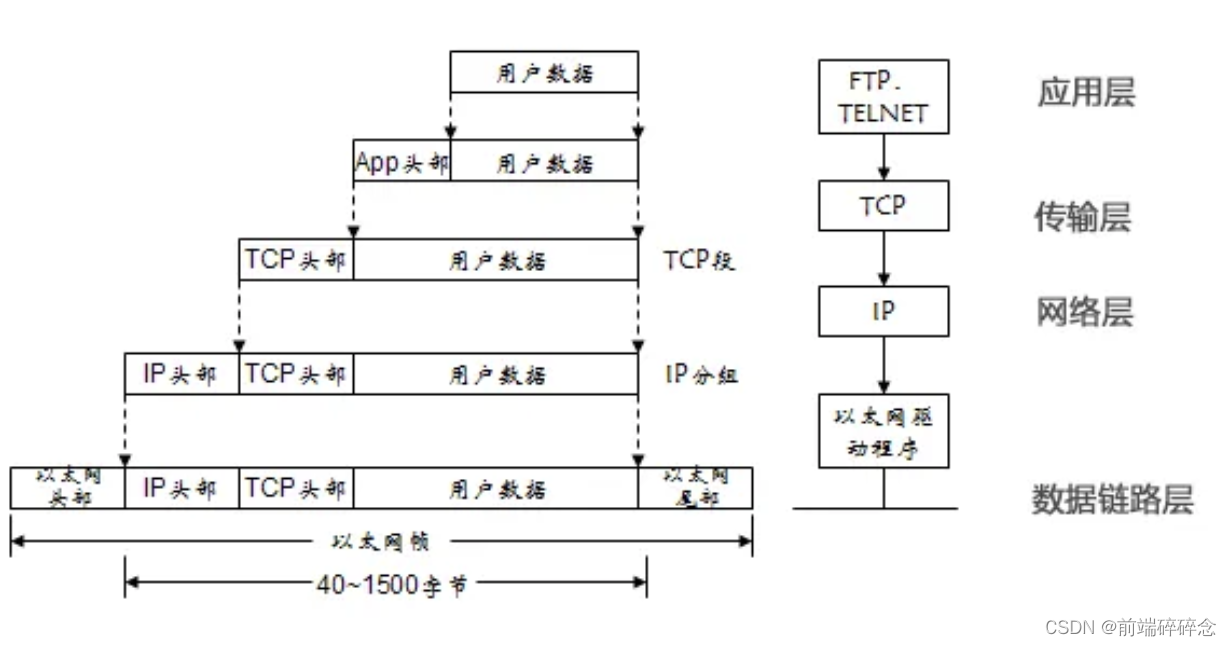
OSI笔记
由7层组成,由下自上分别为: 物理层(硬件方面,例如物理网络设备、布线电缆、光纤等), 传输数据主要是比特流0 1 、电信号数据链路层(确定了0 1 的分组方式,通过广播的方式࿰…...

C++之前置声明
在C中,前置声明是一种声明类或函数的方式,但并不定义它们。 前置声明的主要目的是为了解决编译时的依赖性问题,提高编译效率,并允许更灵活的代码组织。 原理 C前置声明可以减少头文件依赖的原理在于,通过前置声明&am…...
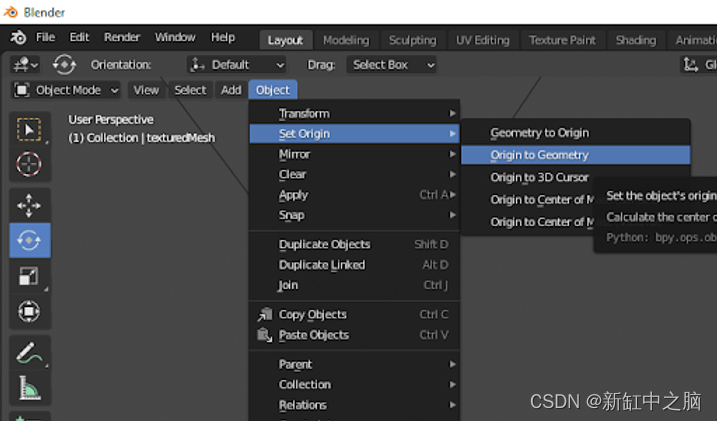
用3D扫描生成合成数据
合成数据集(Synthetic Datasets)正在成为计算机视觉模型训练的标准部分。 虽然新工具使合成数据集变得更容易访问,但除了标准机器学习过程之外,许多工具还需要对 3D 建模有基本的了解。 最简单的捷径是从现实世界中获取现有对象并…...

pip安装依赖报错
执行命令时 pip install --upgrade pip 报错: pip : 无法将“pip”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。请检查名称的拼写,如果包括路径,请确保路径正确,然后再试一次。pip install --upgrade pip~~~ Category…...

规范的项目流程图怎么写
编写规范的项目流程图可以遵循以下步骤: 1.明确项目目标:首先,明确项目的目标以及需要实现的结果。这有助于确定项目的范围和要求。 2.识别项目任务:识别和列出所有的任务,这可以包括获得资源、实施动作、收集信息等…...

模型部署笔记--Pytorch-FX量化
目录 1--Pytorch-FX量化 2--校准模型 3--代码实例 3-1--主函数 3-2--prepare_dataloader函数 3-3--训练和测试函数 1--Pytorch-FX量化 Pytorch在torch.quantization.quantize_fx中提供了两个API,即prepare_fx和convert_fx。 prepare_fx的作用是准备量化&#…...

解决XXLJOB重复执行问题--Redis加锁+注解+AOP
基于Redis加锁注解AOP解决JOB重复执行问题 现象解决方案自定义注解定义AOP策略redis 加锁实践 现象 线上xxljob有时候会遇到同一个任务在调度的时候重复执行,如下图: 线上JOB服务运行了2个实例,有时候会重复调度到同一个实例,有…...
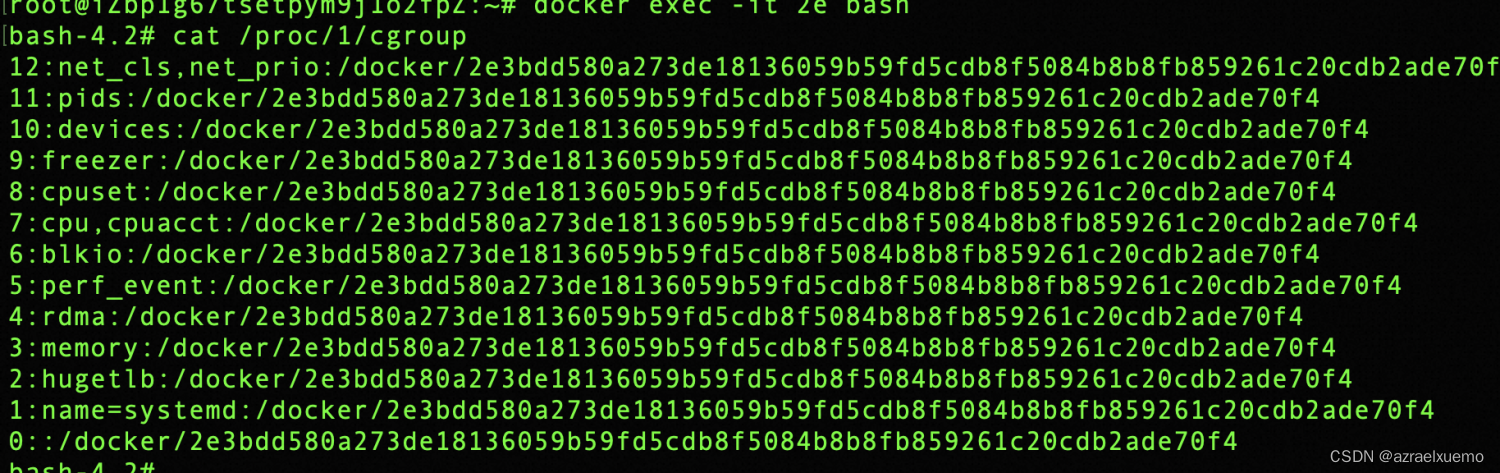
云安全(1)--初识容器逃逸之特权容器逃逸
文章目录 前言privileged,特权容器逃逸环境配置实际利用实际环境利用计划任务/var/spool/cron/crontabs/ 适用于ubuntu debain/var/spool/cron 适用于centos ld.so.preloadssh 前言 在10.15号的上海中华武数杯的渗透赛里做到了一个k8s的题目,这应该是我第一次在比赛…...
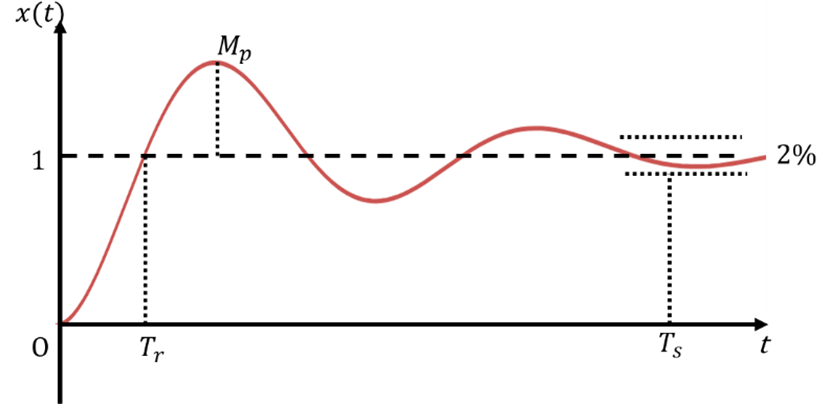
二阶系统时域响应
二阶系统微分方程 二阶系统传递函数 二阶系统单位阶跃响应 过阻尼系统 临界阻尼系统 欠阻尼系统 无阻尼系统 二阶系统阶跃响应仿真 在Matlab中进行仿真,设置不同阻尼比2、1、0.5和0,可以得到结论: 阻尼比越小,系统响应速度越快&…...
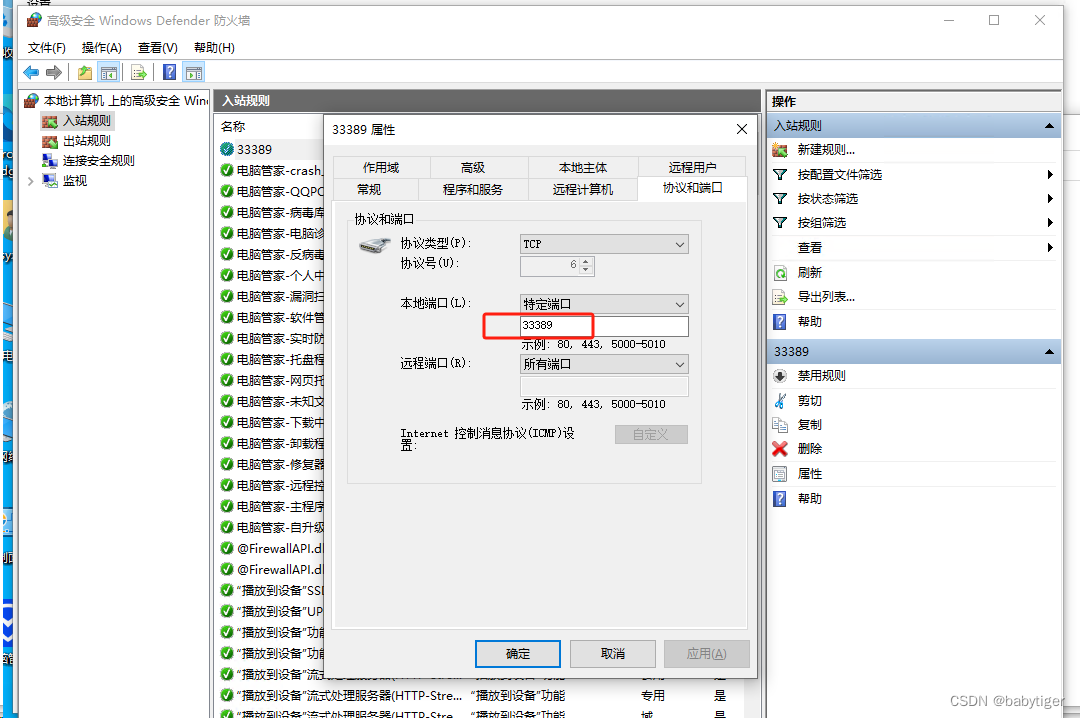
mstsc改端口为33389
windows 远程默认端口3389不太安全,改成33389防下小人 把下面的2个文本存在后缀.reg的文件,双击导入注册表,"PortNumber"dword:0000826d 这个就是33389对应的端口号的16进制值,要想自己改成其它的换下值即可 Windows …...
经典算法试题(二)
文章目录 一、岁数1、题目2、思路讲解3、代码实现4、结果 二、打碎的鸡蛋1、题目2、思路讲解3、代码实现4、结果 三、分糖1、题目2、思路讲解3、代码实现4、结果 四、兔子产子1、题目2、思路讲解3、代码实现4、结果 五、矩阵问题1、题目2、思路讲解3、代码实现4、结果 六、谁是…...

Linux——生产者消费者模型
目录 一.为何要使用生产者消费者模型 二.生产者消费者模型优点 三.基于BlockingQueue的生产者消费者模型 1.BlockingQueue——阻塞队列 2.实现代码 四.POSIX信号量 五.基于环形队列的生产消费模型 一.为何要使用生产者消费者模型 生产者消费者模式就是通过一个容器来解决生…...

Oracle缓存表
Oracle缓存表(db_buffer_pool)由三部分组成: buffer_pool_defualt buffer_pool_keep buffer_pool_recycle 如果要把表钉死在内存中,也就是把表钉在keep区。相关的命令为: alter table 表名 storage(buffer_pool k…...

智能变电站自动化系统的应用与产品选型
摘要:现如今,智能变电站发展已经成为了电力系统发展过程中的内容,如何提高智能变电站的运行效率也成为电力系统发展的一个重要目标,为了能够更好地促进电力系统安全稳定运行,本文则就智能变电站自动化系统的实现进行了…...

reactnative 底部tab页面@react-navigation/bottom-tabs
使用react-navigation/native做的页面导航和tab‘ 官网:https://reactnavigation.org/docs/getting-started 效果图 安装 npm install react-navigation/nativenpm install react-navigation/bottom-tabs封装tabbar.js import { View, StyleSheet, Image } from …...

运维中心—监控大盘
一、监控大盘内容分类 1、告警 2、业务趋势 3、异常码 4、主机 5、服务状态 6、系统账单 二、API分类 【基础数据】 1、分组查询各自子系统 2、子系统查询名下各个微服务 【主机】 根据分组查询主机信息,按照子系统分组,按照CPU和内存排序 步骤…...
Node.js的安装
直接在浏览器中搜索Node.js即可 打开下载好的文件 验证是否安装成功 在cmd中输入 node -v,若结果为版本号那就是成功的 环境配置 配置全局模块所在的路径缓存cache的路径 在安装目录中新建两个文件夹,文件夹名为:node_cache和node_global 输…...

vsCode git 修改、清空、重置、保存账号名密码
1、保存账号名密码,之后拉取代码都不用重新输入: git config --global credential.helper store 2、查看git用户名: git config user.name 3、清空所有的用户名和密码: git config --system --unset credential.helper 4、清…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...
