第三章 内存管理 十三、页面置换算法(最佳置换算法、先进先出置换算法、最近最久未使用置换算法、时钟置换算法、改进型的时钟置换算法)
目录
一、定义
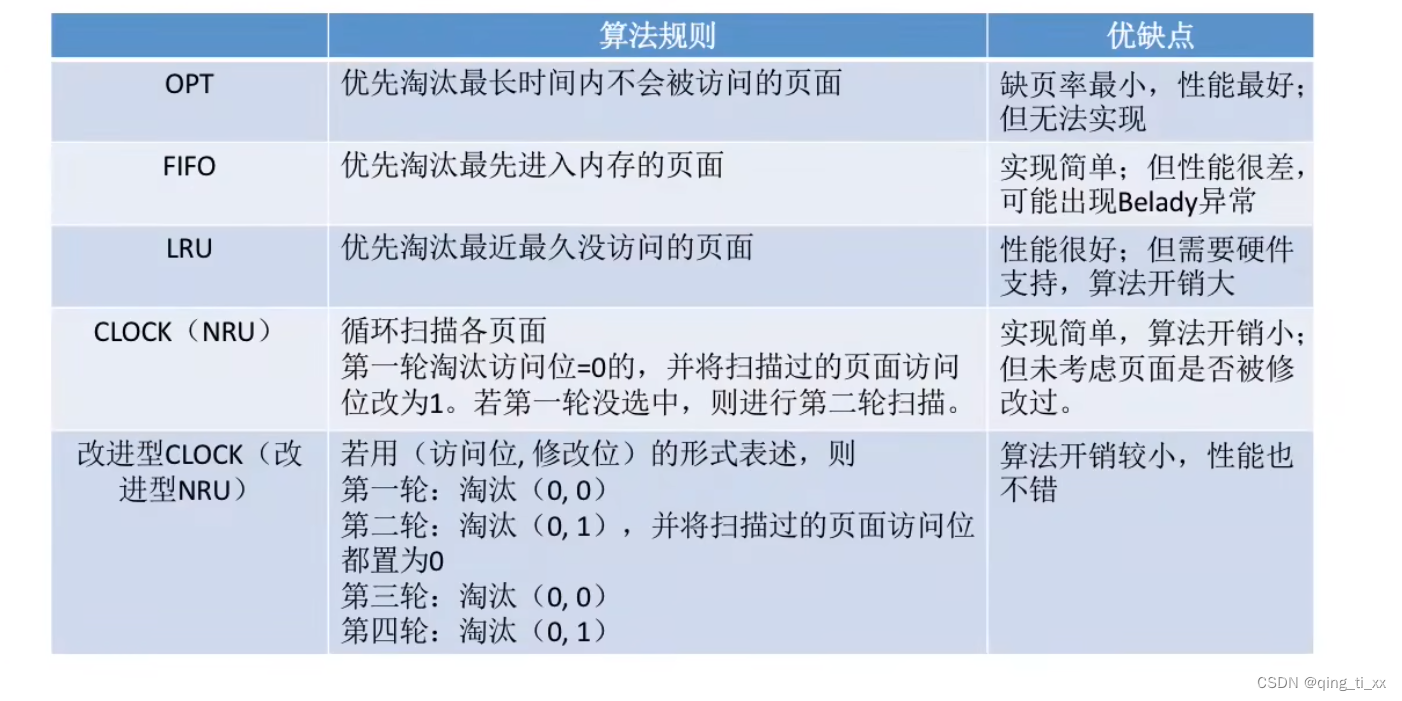
二、分类
1、最佳置换算法 / 最远置换算法(OPT,Optimal):
1.1、定义:
1.2、例子:
2、先进先出置换算法(FIFO):
2.1、定义:
2.2、实现方法:
2.3、例子:
3、最近最久未使用置换算法(LRU,least recently used):
3.1、定义:
3.2、实现方法:
3.3、例子:
4、时钟置换算法是一种性能和开销较均衡的算法,又称CLOCK算法,或最近未用算法(NRU,NotRecently Used)
4.1、简单的CLOCK算法实现方法:
4.2、例子:
5、改进型的时钟置换算法
5.1、实现方式
三、总结
一、定义
页面置换算法是指在操作系统中,当需要调入一个页面时,若所有的物理页面已被占用,则需要选择一个页面进行置换。页面置换算法是解决内存不足的问题,从而实现更多程序同时运行的重要手段之一。
二、分类
1、最佳置换算法 / 最远置换算法(OPT,Optimal):
1.1、定义:
每次选择淘汰的页面将是以后永不使用,或者在最长时间内不再被访问的页面,这样可以保证最低的缺页率。
1.2、例子:

(1)在上例中,首先依次访问页面,并将页面放入内存块中,直到内存块装满。
(2)装满后,接下来要访问的是2号页面;
(3)根据OPT算法规则,我们依次往后查看要访问的页面,发现在0,1,7三个页面中,页面7是最远会被访问的。
(4)所以,我们就会将内存块中的7页面淘汰,替换为页面2装入。
(5)依此类推,整个过程缺页中断发生了9次,页面置换发生了6次.(前3次没有发生页面置换)
缺页率:缺页次数 / 总的访问次数

注意:缺页时未必发生页面置换。若还有可用的空闲内存块,就不用进行页面置换。

2、先进先出置换算法(FIFO):
2.1、定义:
每次选择淘汰的页面是最早进入内存的页面
2.2、实现方法:
把调入内存的页面根据调入的先后顺序排成一个队列,需要换出页面时选择队头页面即可。
队列的最大长度取决于系统为进程分配了多少个内存块。
2.3、例子:

(1)在上例中,首先依次访问页面,并将页面放入内存块中,直到内存块装满。
(2)下一个访问的是页面0,此时就要把最早进来的页面3淘汰。
(3)替换为页面0.

3、最近最久未使用置换算法(LRU,least recently used):
3.1、定义:
每次淘汰的页面是最近最久未使用的页面
3.2、实现方法:
赋予每个页面对应的页表项中,用访问字段记录该页面自上次被访问以来所经历的时间t。
当需要淘汰一个页面时,选择现有页面中t值最大的,即最近最久未使用的页面。
3.3、例子:

(1)在上例中,首先依次访问页面,并将页面放入内存块中,直到内存块装满。
(2)一直访问,直到访问到页面3时。
(3)在此之前,我们依次访问过了7,2,1,8,所以7是最久没有被访问的。
(4)所以将7替换为3.

4、时钟置换算法是一种性能和开销较均衡的算法,又称CLOCK算法,或最近未用算法(NRU,NotRecently Used)
4.1、简单的CLOCK算法实现方法:
- 为每个页面设置一个访问位,再将内存中的页面都通过链接指针链接成一个循环队列。
- 当某页被访问时,其访问位置为1。当需要淘汰一个页面时,只需检查页的访问位。
- 如果是0,就选择该页换出;如果是1,则将它置为0,暂不换出,继续检查下一个页面,若第一轮扫描中所有页面都是1,则将这些页面的访问位依次置为O后,再进行第二轮扫描(第二轮扫描中一定会有访问位为0的页面,因此简单的CLOCK算法选择一个淘汰页面最多会经过两轮扫描)
4.2、例子:

(1)若我们有如上例子,且有5个内存块,在依次访问了1,3,4,2,5后,我们会得到如下视图

(2)此时这几个内存块都被访问过,所以它们的访问位都为1.
(3)我们从1号页面依次扫描,而且要将经过的访问位为1的页面的访问位改为0,并且找到访问位为0的页面。
(4)在上图中,我们找了一圈也没有找到访问位为0的页面,而且我们将它全部重置为0了。

(5)然后我们进行第二次扫描,发现1号页为0,所以淘汰它,并且替换为6号页

(6)接下来访问3,4,7;
因为有3号页了,所以指针不动,只是将3号页的访问位改为1;
4号页同样如此。

(7)然后访问7,此时转动指针,将3,4的访问位改为0;而且找到了2号页的访问位为0;所以将7号页存到下方。

5、改进型的时钟置换算法

5.1、实现方式
(1)和简单时钟置换算法相似,其实就是将找0,改为了找(0,0);
(2)只不过第一轮并不会相简单的那样将1改为0;
(3)而是,如果第一轮没有找到(0,0),就会将(0,1)看作(0,0)进行淘汰。
(4)在第二轮的查找中,会将访问位重置为0

(5)找到为(0,0)的页淘汰
(6)若是如下例子

(7)第一轮扫描(0,0),发现都不是。
(8)第二轮扫描(0,1),且被扫描过的页面的访问位都会被置为0

(9)第三轮扫描(0,0),没找到,不改变什么
(10)第四轮扫描,将(0,1)当作(0,0)淘汰

三、总结
相关文章:

第三章 内存管理 十三、页面置换算法(最佳置换算法、先进先出置换算法、最近最久未使用置换算法、时钟置换算法、改进型的时钟置换算法)
目录 一、定义 二、分类 1、最佳置换算法 / 最远置换算法(OPT,Optimal): 1.1、定义: 1.2、例子: 2、先进先出置换算法(FIFO): 2.1、定义: 2.2、实现方法: 2.3、例子: 3、最…...

连接到EC2,开启root登录
1.启动完新实例,下载密钥对密钥对登录 ssh -i "ec2-user.pem" ec2-userec2-xx-xx-xx-xx.compute-1.amazonaws.com2.为root设置密码 sudo passwd root3.切换到root权限 su root4.修改ssh配置文件,允许密码登陆 vi /etc/ssh/sshd_config Pas…...
线性代数-Python-02:矩阵的基本运算 - 手写Matrix及numpy中的用法
文章目录 一、代码仓库二、矩阵的基本运算2.1 矩阵的加法2.2 矩阵的数量乘法2.3 矩阵和向量的乘法2.4 矩阵和矩阵的乘法2.5 矩阵的转置 三、手写Matrix代码Matrix.pymain_matrix.pymain_numpy_matrix.py 一、代码仓库 https://github.com/Chufeng-Jiang/Python-Linear-Algebra-…...

6.MySQL内置函数
个人主页:Lei宝啊 愿所有美好如期而遇 日期函数 current_date() 当前日期 select 可以做表达式和函数的计算。 current_time() 当前时间 current_timestamp() 当前日期加时间 注意:值得说明的是这三个函数底层调用的都是同一个函数,只不…...
3dmax中导出模型到unity注意事项
从3dmax中导出 1. 注意单位,根据需要,选英寸还是选厘米 2. 不能导出有错误的骨骼,否则导入后模型网格里出现 Skinned Mesh Renderer ,对网格变换移动有影响,正常情况下都应该是 Mesh Renderer 3. 导出一般不带光源和…...
QTday05(TCP的服务端客户端通信)
实现聊天室功能 服务端代码: pro文件需要导入 network 头文件: #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QTcpServer>//服务端 #include <QTcpSocket>//客户端 #include <QList> #include <QMes…...
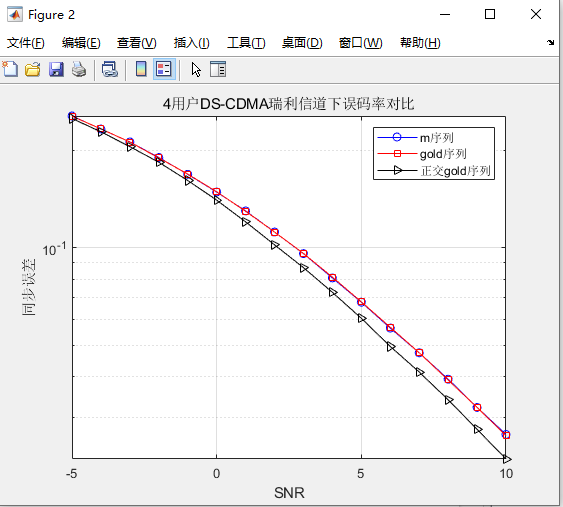
【MATLAB源码-第52期】基于matlab的4用户DS-CDMA误码率仿真,对比不同信道以及不同扩频码。
操作环境: MATLAB 2022a 1、算法描述 1. DS-CDMA系统 DS-CDMA (Direct Sequence Code Division Multiple Access) 是一种多址接入技术,其基本思想是使用伪随机码序列来调制发送信号。DS-CDMA的特点是所有用户在同一频率上同时发送和接收信息…...

Spring 路径与占位符
SpringMVC支持ant风格的路径 ?:表示任意的单个字符 *:表示任意的0个或多个字符 \**:表示任意的一层或多层目录 注意:在使用**时,只能使用/**/xxx的方式 1.测试 ? <a th:href"{/succe…...
MIT 6.824 -- Cache Consistency -- 11
MIT 6.824 -- Cache Consistency -- 11 引言严峻挑战锁服务缓存一致性问题案例演示优化 原子性问题故障恢复问题log内容故障恢复 小结 课程b站视频地址: MIT 6.824 Distributed Systems Spring 2020 分布式系统 推荐伴读读物: 极客时间 – 大数据经典论文解读DDIA – 数据密集…...
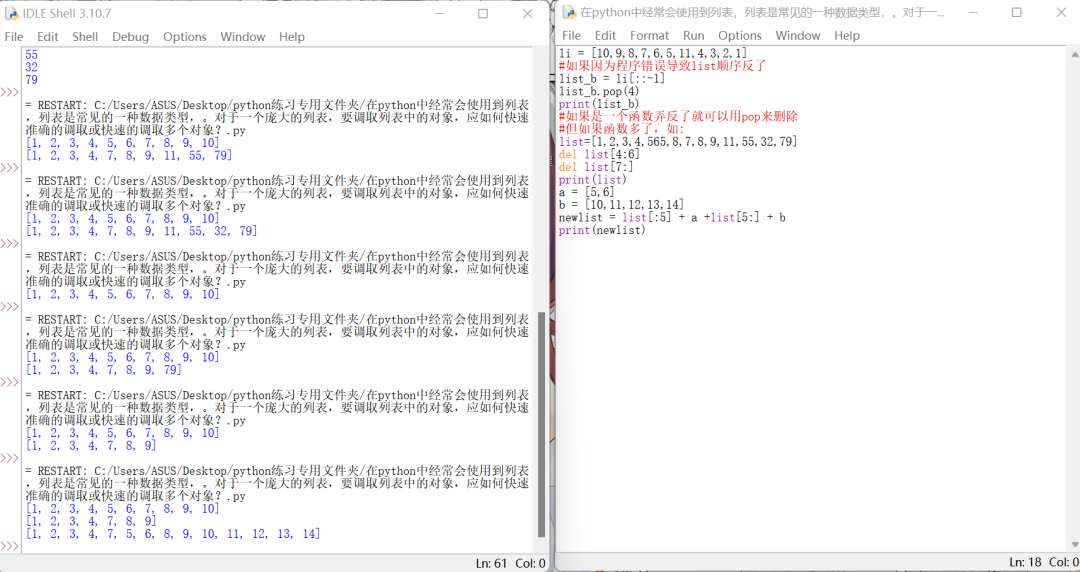
Python在列表中如何对多个参数进行修改
1 问题 在python中经常会使用到列表,列表是常见的一种数据类型。对于一个庞大的列表,要调取列表中的对象,应如何快速准确的调取或快速的调取多个对象? 2 方法 解决问题的步骤采用如下方式: 基本的,已知元素…...

手机启用adb无线调试
具体步骤 手机和电脑处于同一个路由器下。 比如手机IP是192.168.31.181,电脑能ping通。 手机端启用无线adb调试先把手机用USB线连接电脑,打开adb,输入以下命令: G:\> adb tcpip 5555 restarting in TCP mode port: 5555 无…...

openGauss学习笔记-105 openGauss 数据库管理-管理用户及权限-默认权限机制
文章目录 openGauss学习笔记-105 openGauss 数据库管理-管理用户及权限-默认权限机制 openGauss学习笔记-105 openGauss 数据库管理-管理用户及权限-默认权限机制 数据库对象创建后,进行对象创建的用户就是该对象的所有者。openGauss安装后的默认情况下,…...
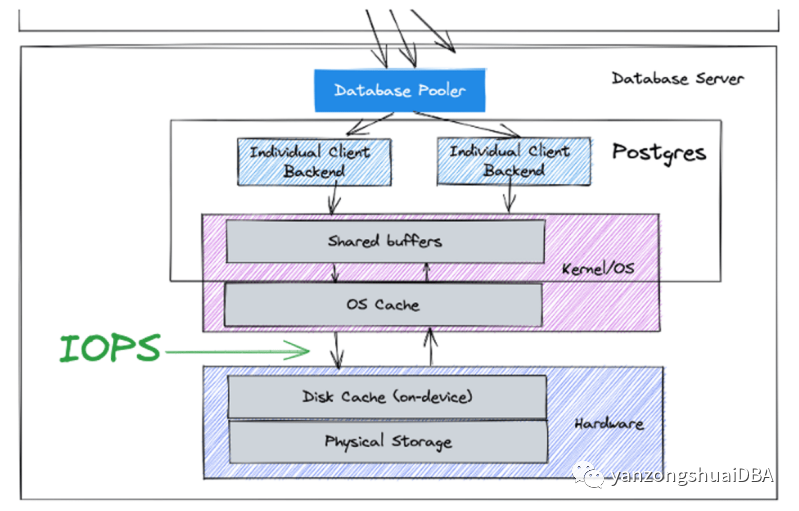
[翻译]理解Postgres的IOPS:为什么数据即使都在内存,IOPS也非常重要
理解Postgres的IOPS:为什么数据即使都在内存,IOPS也非常重要 磁盘IOPS(每秒输入/输出操作数)是衡量磁盘系统性能的关键指标。代表每秒可以执行的读写操作数量。对于严重依赖于磁盘访问的PG来说,了解和优化磁盘IOPS对实…...
Day6力扣打卡
打卡记录 统计无向图中无法互相到达点对数(并查集 / DFS) 链接 并查集 思路:用并查集将连通区域的连在一起,再遍历所有点,用hash表存储不同连通块的元素个数,然后 乘积和 便是答案。 注意: /…...

10月面试js基础
作用域 变量的可用范围 作用域链 保存的变量的使用顺序的一个链(也就是路线图), 被称为作用域链。 当在Javascript中使用一个变量的时候,首先Javascript引擎会尝试在当前作用域下去寻找该变量,如果没找到,再…...

研发日常踩坑-Mysql分页数据重复 | 京东云技术团队
踩坑描述: 写分页查询接口,order by和limit混用的时候,出现了排序的混乱情况 在进行第N页查询时,出现与第一前面页码的数据一样的记录。 问题 在MySQL中分页查询,我们经常会用limit,如:limit(0,20)表示查询第一页的…...

Ubuntu18.04安装QGC报错 `GLIBC_2.29‘ not found
按照官网教程,最后运行时出错。 /tmp/.mount_QGroun2NOhPP/QGroundControl: /lib/x86_64-linux-gnu/libm.so.6: version GLIBC_2.29 not found (required by /tmp/.mount_QGroun2NOhPP/QGroundControl) /tmp/.mount_QGroun2NOhPP/QGroundControl: /usr/lib/x86_64-…...

回归预测 | MATLAB实现BO-GRU贝叶斯优化门控循环单元多输入单输出回归预测
回归预测 | MATLAB实现BO-GRU贝叶斯优化门控循环单元多输入单输出回归预测 目录 回归预测 | MATLAB实现BO-GRU贝叶斯优化门控循环单元多输入单输出回归预测效果一览基本介绍模型搭建程序设计参考资料 效果一览 基本介绍 MATLAB实现BO-GRU贝叶斯优化门控循环单元回归预测。基于贝…...

Easyx趣味编程7,鼠标消息读取及音频播放
hello大家好,这里是dark flame master,今天给大家带来Easyx图形库最后一节功能实现的介绍,前边介绍了绘制各种图形及键盘交互,文字,图片等操作,今天就可以使写出的程序更加生动且容易操控。一起学习吧&…...
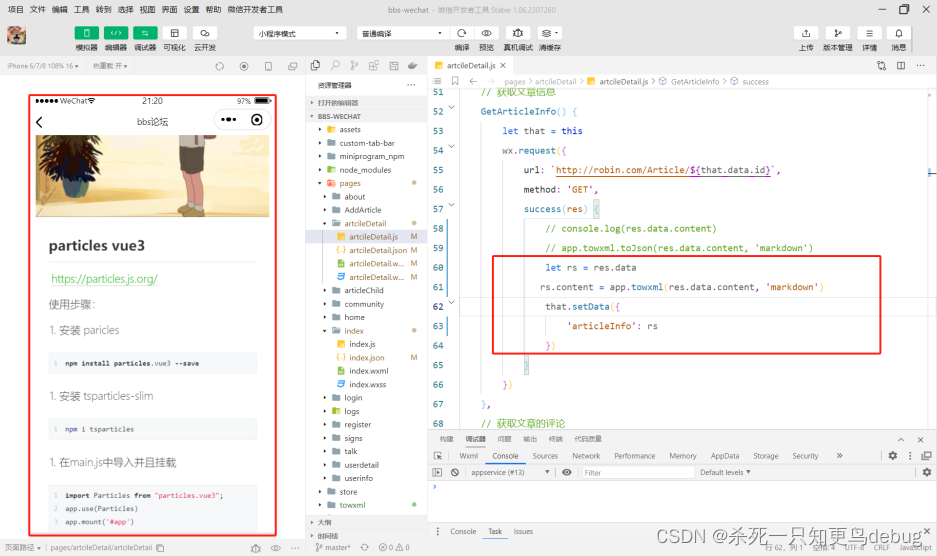
towxml的使用,在微信小程序中快速将markdown格式渲染为wxml文本
towxml的使用,在微信小程序中快速将markdown格式渲染为wxml文本 Towxml概述安装下载 Towxml在小程序中使用 towxml Towxml概述 towxml3.0 支持以下功能: ● echarts图表,默认禁用,需自行构建以开启此功能 ● LaTeX数学公式&#…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...
