线性代数-Python-02:矩阵的基本运算 - 手写Matrix及numpy中的用法
文章目录
- 一、代码仓库
- 二、矩阵的基本运算
- 2.1 矩阵的加法
- 2.2 矩阵的数量乘法
- 2.3 矩阵和向量的乘法
- 2.4 矩阵和矩阵的乘法
- 2.5 矩阵的转置
- 三、手写Matrix代码
- Matrix.py
- main_matrix.py
- main_numpy_matrix.py
一、代码仓库
https://github.com/Chufeng-Jiang/Python-Linear-Algebra-for-Beginner/tree/main
二、矩阵的基本运算
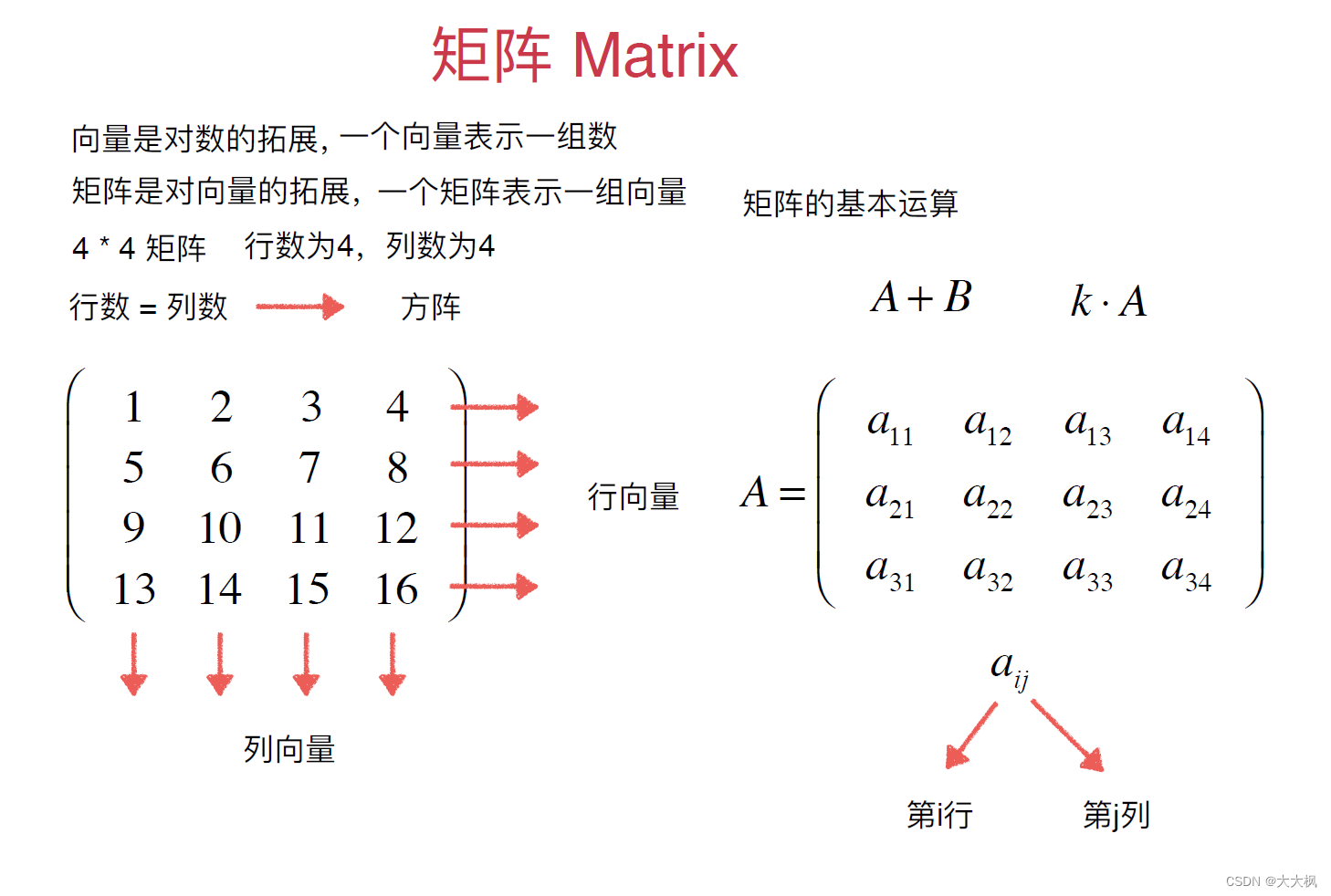
2.1 矩阵的加法
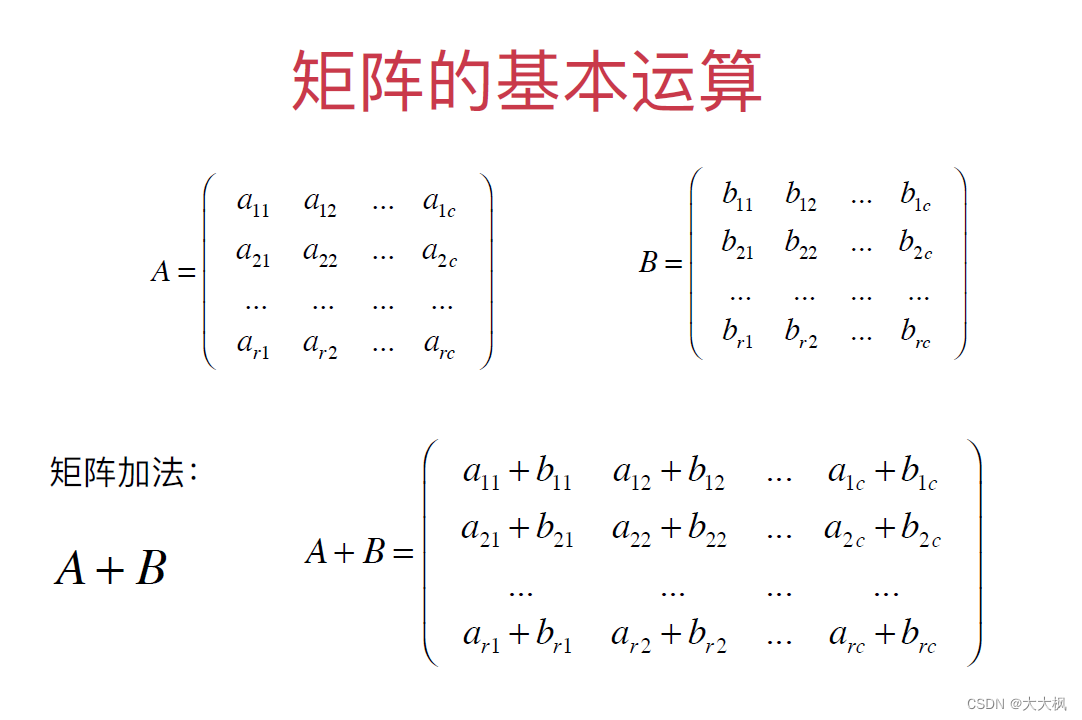
2.2 矩阵的数量乘法
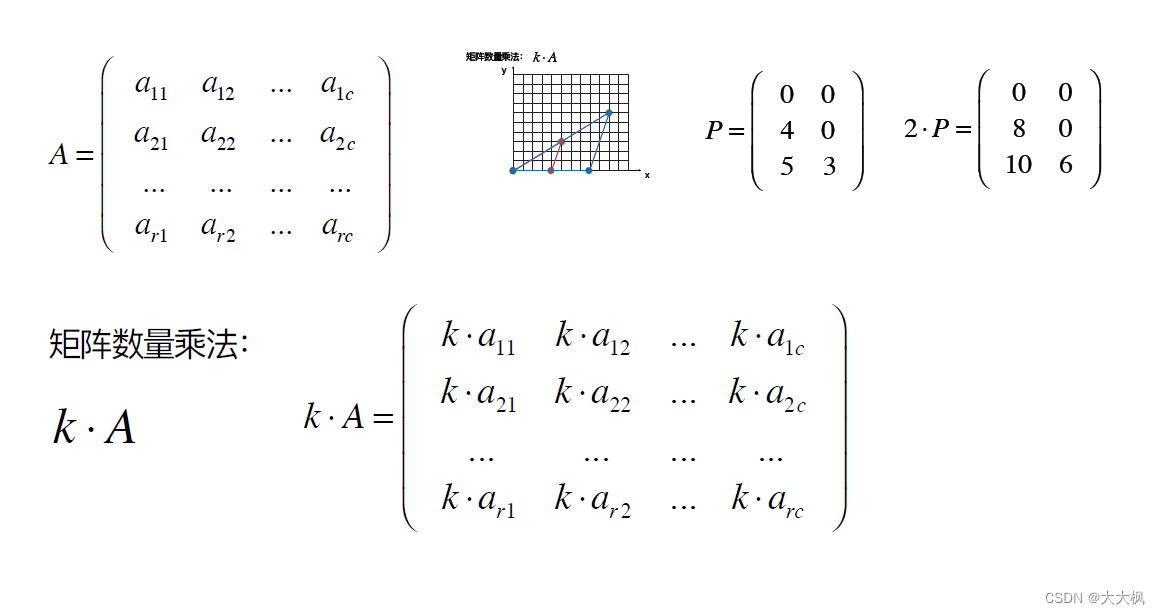
2.3 矩阵和向量的乘法
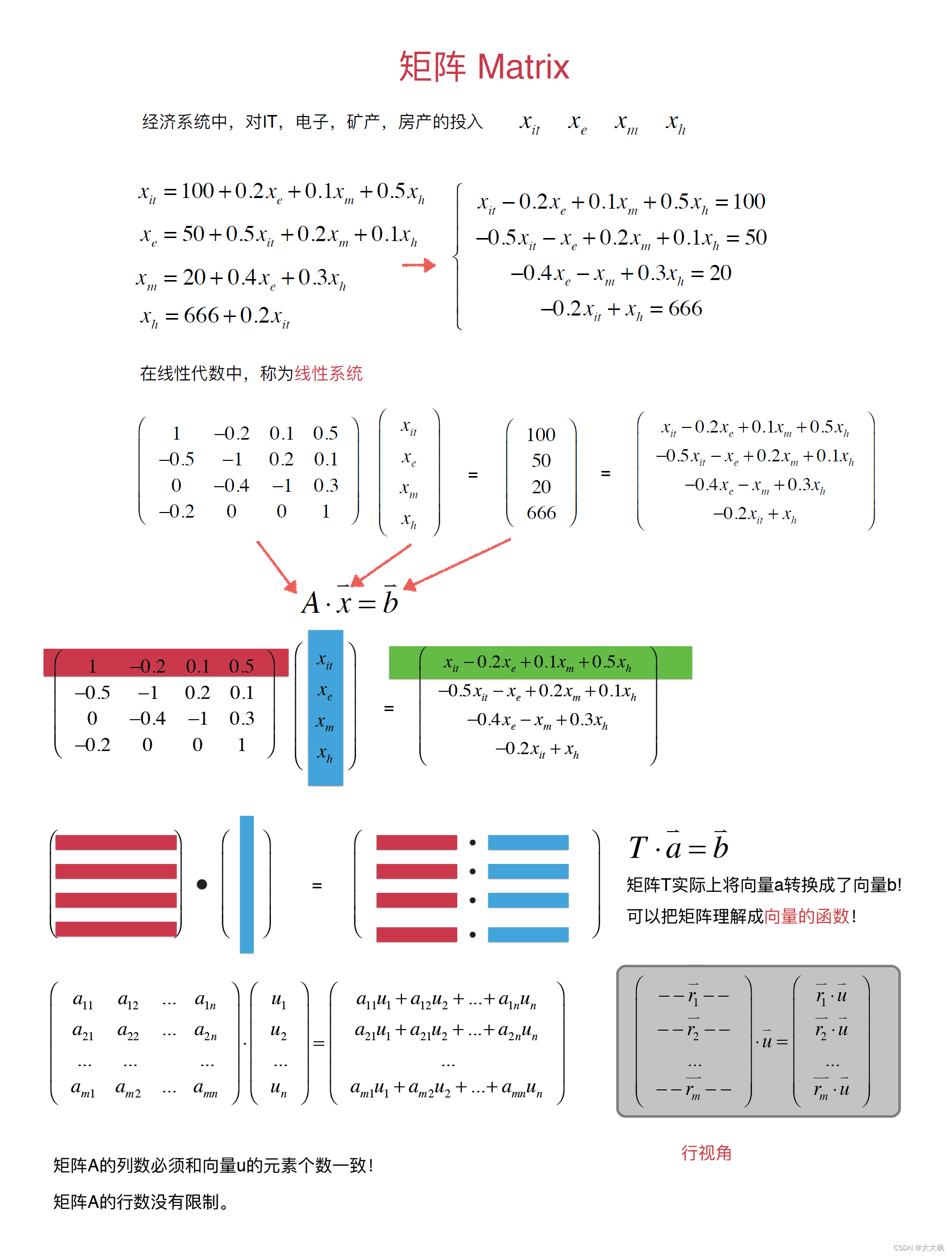
2.4 矩阵和矩阵的乘法


2.5 矩阵的转置

三、手写Matrix代码
Matrix.py
from .Vector import Vectorclass Matrix:"""参数二:是一个二维列表"""def __init__(self, list2d):self._values = [row[:] for row in list2d]@classmethoddef zero(cls, r, c):"""返回一个r行c列的零矩阵"""return cls([[0] * c for _ in range(r)])def T(self):"""返回矩阵的转置矩阵"""return Matrix([[e for e in self.col_vector(i)]for i in range(self.col_num())])def __add__(self, another):"""返回两个矩阵的加法结果"""assert self.shape() == another.shape(), \"Error in adding. Shape of matrix must be same."return Matrix([[a + b for a, b in zip(self.row_vector(i), another.row_vector(i))]for i in range(self.row_num())])def __sub__(self, another):"""返回两个矩阵的减法结果"""assert self.shape() == another.shape(), \"Error in subtracting. Shape of matrix must be same."return Matrix([[a - b for a, b in zip(self.row_vector(i), another.row_vector(i))]for i in range(self.row_num())])def dot(self, another):"""返回矩阵乘法的结果"""if isinstance(another, Vector):# 矩阵和向量的乘法assert self.col_num() == len(another), \"Error in Matrix-Vector Multiplication."return Vector([self.row_vector(i).dot(another) for i in range(self.row_num())])if isinstance(another, Matrix):# 矩阵和矩阵的乘法assert self.col_num() == another.row_num(), \"Error in Matrix-Matrix Multiplication."return Matrix([[self.row_vector(i).dot(another.col_vector(j)) for j in range(another.col_num())]for i in range(self.row_num())])def __mul__(self, k):"""返回矩阵的数量乘结果: self * k"""return Matrix([[e * k for e in self.row_vector(i)]for i in range(self.row_num())])def __rmul__(self, k):"""返回矩阵的数量乘结果: k * self"""return self * kdef __truediv__(self, k):"""返回数量除法的结果矩阵:self / k"""return (1 / k) * selfdef __pos__(self):"""返回矩阵取正的结果"""return 1 * selfdef __neg__(self):"""返回矩阵取负的结果"""return -1 * selfdef row_vector(self, index):"""返回矩阵的第index个行向量"""return Vector(self._values[index])def col_vector(self, index):"""返回矩阵的第index个列向量"""return Vector([row[index] for row in self._values])def __getitem__(self, pos):"""返回矩阵pos位置的元素"""r, c = posreturn self._values[r][c]def size(self):"""返回矩阵的元素个数"""r, c = self.shape()return r * cdef row_num(self):"""返回矩阵的行数"""return self.shape()[0]__len__ = row_numdef col_num(self):"""返回矩阵的列数"""return self.shape()[1]def shape(self):"""返回矩阵的形状: (行数, 列数)"""return len(self._values), len(self._values[0])def __repr__(self):return "Matrix({})".format(self._values)__str__ = __repr__main_matrix.py
from playLA.Vector import Vector
from playLA.Matrix import Matrixif __name__ == "__main__":matrix = Matrix([[1, 2], [3, 4]])print(matrix)print("matrix.shape = {}".format(matrix.shape()))print("matrix.size = {}".format(matrix.size()))print("len(matrix) = {}".format(len(matrix)))print("matrix[0][0] = {}".format(matrix[0, 0]))matrix2 = Matrix([[5, 6], [7, 8]])print(matrix2)print("add: {}".format(matrix + matrix2))print("subtract: {}".format(matrix - matrix2))print("scalar-mul: {}".format(2 * matrix))print("scalar-mul: {}".format(matrix * 2))print("zero_2_3: {}".format(Matrix.zero(2, 3)))T = Matrix([[1.5, 0], [0, 2]])p = Vector([5, 3])print("T.dot(p) = {}".format(T.dot(p)))P = Matrix([[0, 4, 5], [0, 0, 3]])print("T.dot(P) = {}".format(T.dot(P)))print("A.dot(B) = {}".format(matrix.dot(matrix2)))print("B.dot(A) = {}".format(matrix2.dot(matrix)))print("P.T = {}".format(P.T()))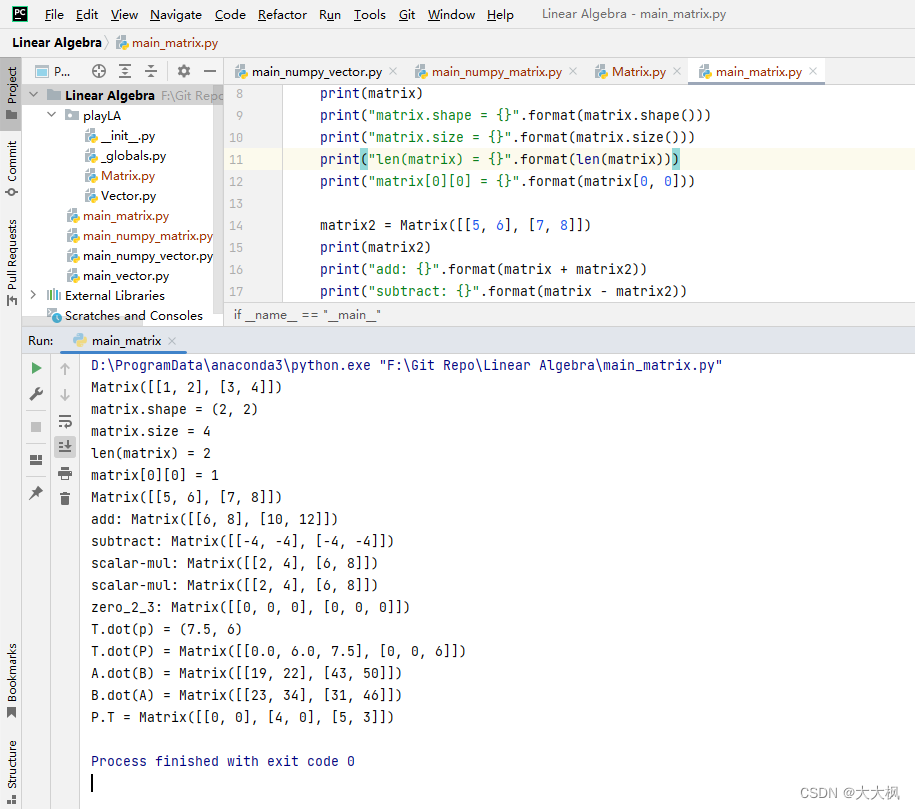
main_numpy_matrix.py
import numpy as npif __name__ == "__main__":# 矩阵的创建A = np.array([[1, 2], [3, 4]])print(A)# 矩阵的属性print(A.shape)print(A.T)# 获取矩阵的元素print(A[1, 1])print(A[0])print(A[:, 0])print(A[1, :])# 矩阵的基本运算B = np.array([[5, 6], [7, 8]])print(A + B)print(A - B)print(10 * A)print(A * 10)print(A * B)print(A.dot(B))p = np.array([10, 100])print(A + p)print(A + 1)print(A.dot(p))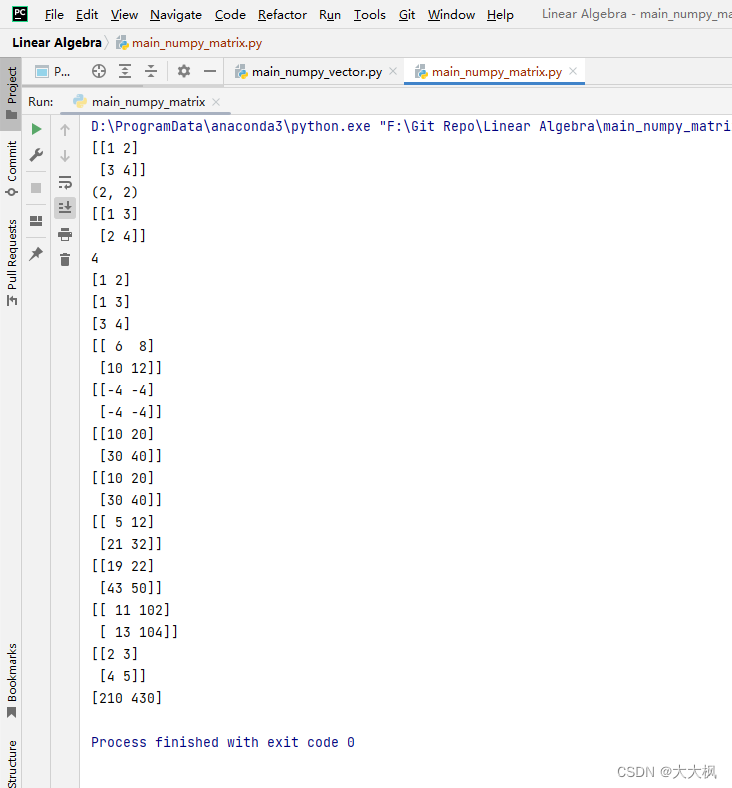
相关文章:

线性代数-Python-02:矩阵的基本运算 - 手写Matrix及numpy中的用法
文章目录 一、代码仓库二、矩阵的基本运算2.1 矩阵的加法2.2 矩阵的数量乘法2.3 矩阵和向量的乘法2.4 矩阵和矩阵的乘法2.5 矩阵的转置 三、手写Matrix代码Matrix.pymain_matrix.pymain_numpy_matrix.py 一、代码仓库 https://github.com/Chufeng-Jiang/Python-Linear-Algebra-…...

6.MySQL内置函数
个人主页:Lei宝啊 愿所有美好如期而遇 日期函数 current_date() 当前日期 select 可以做表达式和函数的计算。 current_time() 当前时间 current_timestamp() 当前日期加时间 注意:值得说明的是这三个函数底层调用的都是同一个函数,只不…...
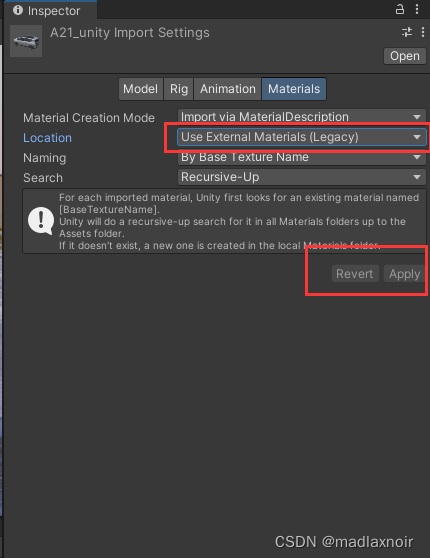
3dmax中导出模型到unity注意事项
从3dmax中导出 1. 注意单位,根据需要,选英寸还是选厘米 2. 不能导出有错误的骨骼,否则导入后模型网格里出现 Skinned Mesh Renderer ,对网格变换移动有影响,正常情况下都应该是 Mesh Renderer 3. 导出一般不带光源和…...
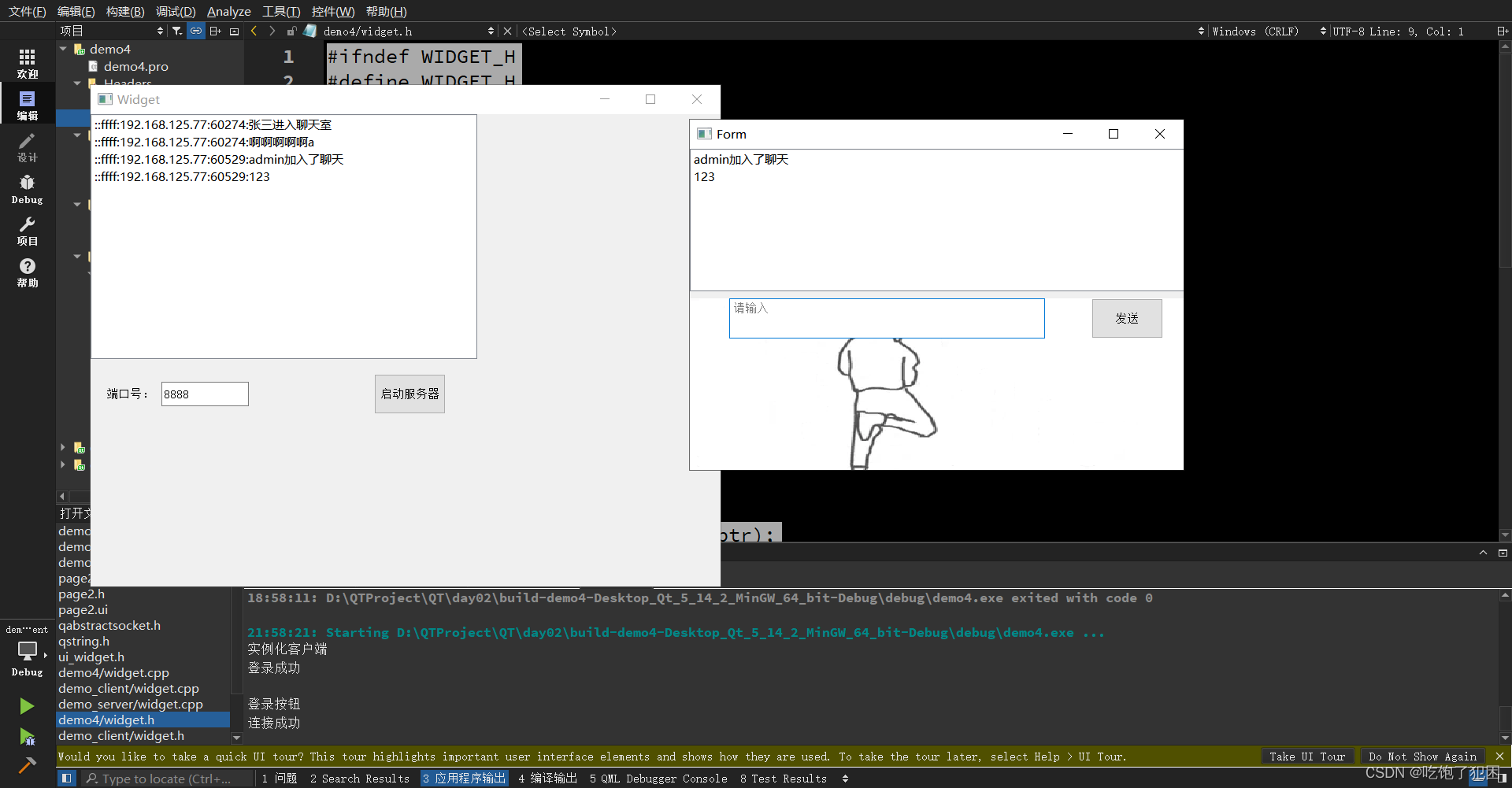
QTday05(TCP的服务端客户端通信)
实现聊天室功能 服务端代码: pro文件需要导入 network 头文件: #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QTcpServer>//服务端 #include <QTcpSocket>//客户端 #include <QList> #include <QMes…...
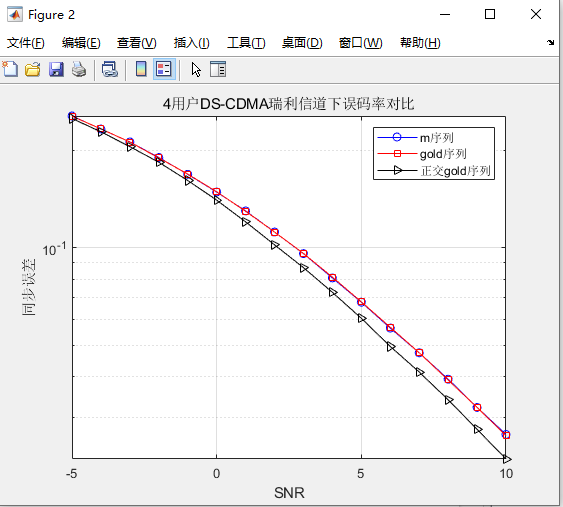
【MATLAB源码-第52期】基于matlab的4用户DS-CDMA误码率仿真,对比不同信道以及不同扩频码。
操作环境: MATLAB 2022a 1、算法描述 1. DS-CDMA系统 DS-CDMA (Direct Sequence Code Division Multiple Access) 是一种多址接入技术,其基本思想是使用伪随机码序列来调制发送信号。DS-CDMA的特点是所有用户在同一频率上同时发送和接收信息…...

Spring 路径与占位符
SpringMVC支持ant风格的路径 ?:表示任意的单个字符 *:表示任意的0个或多个字符 \**:表示任意的一层或多层目录 注意:在使用**时,只能使用/**/xxx的方式 1.测试 ? <a th:href"{/succe…...
MIT 6.824 -- Cache Consistency -- 11
MIT 6.824 -- Cache Consistency -- 11 引言严峻挑战锁服务缓存一致性问题案例演示优化 原子性问题故障恢复问题log内容故障恢复 小结 课程b站视频地址: MIT 6.824 Distributed Systems Spring 2020 分布式系统 推荐伴读读物: 极客时间 – 大数据经典论文解读DDIA – 数据密集…...
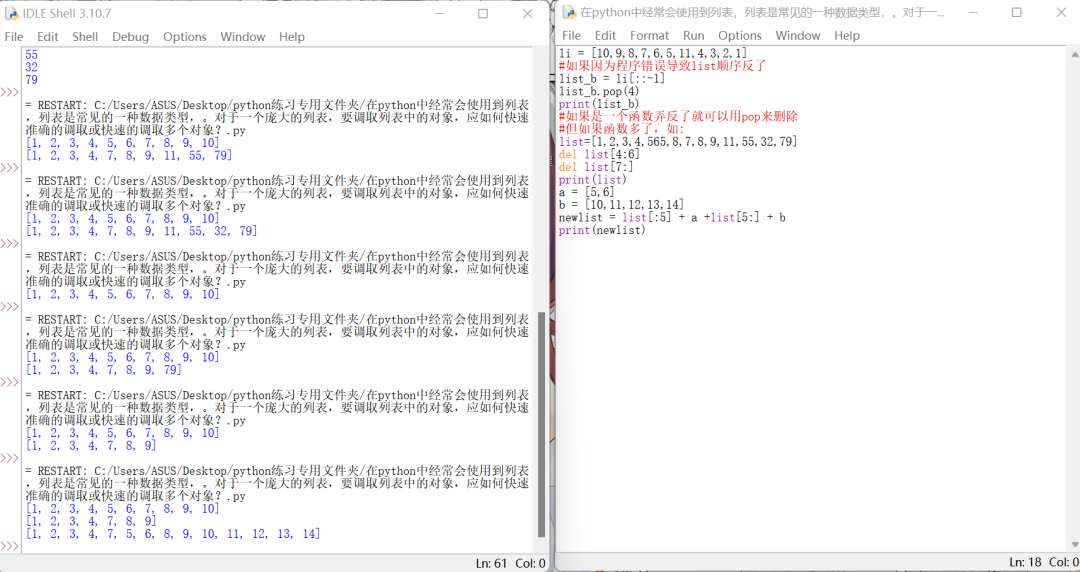
Python在列表中如何对多个参数进行修改
1 问题 在python中经常会使用到列表,列表是常见的一种数据类型。对于一个庞大的列表,要调取列表中的对象,应如何快速准确的调取或快速的调取多个对象? 2 方法 解决问题的步骤采用如下方式: 基本的,已知元素…...

手机启用adb无线调试
具体步骤 手机和电脑处于同一个路由器下。 比如手机IP是192.168.31.181,电脑能ping通。 手机端启用无线adb调试先把手机用USB线连接电脑,打开adb,输入以下命令: G:\> adb tcpip 5555 restarting in TCP mode port: 5555 无…...

openGauss学习笔记-105 openGauss 数据库管理-管理用户及权限-默认权限机制
文章目录 openGauss学习笔记-105 openGauss 数据库管理-管理用户及权限-默认权限机制 openGauss学习笔记-105 openGauss 数据库管理-管理用户及权限-默认权限机制 数据库对象创建后,进行对象创建的用户就是该对象的所有者。openGauss安装后的默认情况下,…...
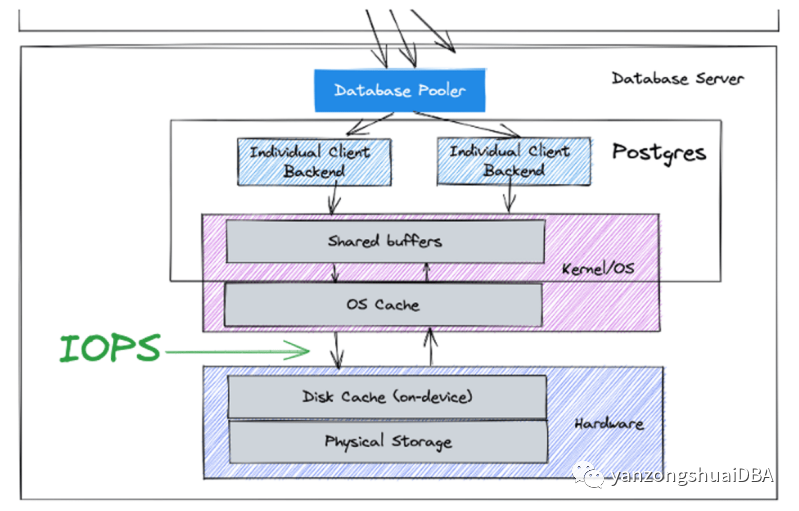
[翻译]理解Postgres的IOPS:为什么数据即使都在内存,IOPS也非常重要
理解Postgres的IOPS:为什么数据即使都在内存,IOPS也非常重要 磁盘IOPS(每秒输入/输出操作数)是衡量磁盘系统性能的关键指标。代表每秒可以执行的读写操作数量。对于严重依赖于磁盘访问的PG来说,了解和优化磁盘IOPS对实…...
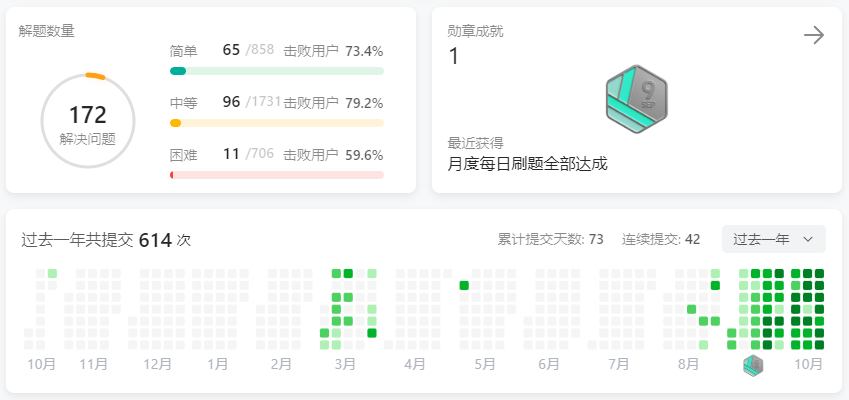
Day6力扣打卡
打卡记录 统计无向图中无法互相到达点对数(并查集 / DFS) 链接 并查集 思路:用并查集将连通区域的连在一起,再遍历所有点,用hash表存储不同连通块的元素个数,然后 乘积和 便是答案。 注意: /…...

10月面试js基础
作用域 变量的可用范围 作用域链 保存的变量的使用顺序的一个链(也就是路线图), 被称为作用域链。 当在Javascript中使用一个变量的时候,首先Javascript引擎会尝试在当前作用域下去寻找该变量,如果没找到,再…...

研发日常踩坑-Mysql分页数据重复 | 京东云技术团队
踩坑描述: 写分页查询接口,order by和limit混用的时候,出现了排序的混乱情况 在进行第N页查询时,出现与第一前面页码的数据一样的记录。 问题 在MySQL中分页查询,我们经常会用limit,如:limit(0,20)表示查询第一页的…...

Ubuntu18.04安装QGC报错 `GLIBC_2.29‘ not found
按照官网教程,最后运行时出错。 /tmp/.mount_QGroun2NOhPP/QGroundControl: /lib/x86_64-linux-gnu/libm.so.6: version GLIBC_2.29 not found (required by /tmp/.mount_QGroun2NOhPP/QGroundControl) /tmp/.mount_QGroun2NOhPP/QGroundControl: /usr/lib/x86_64-…...

回归预测 | MATLAB实现BO-GRU贝叶斯优化门控循环单元多输入单输出回归预测
回归预测 | MATLAB实现BO-GRU贝叶斯优化门控循环单元多输入单输出回归预测 目录 回归预测 | MATLAB实现BO-GRU贝叶斯优化门控循环单元多输入单输出回归预测效果一览基本介绍模型搭建程序设计参考资料 效果一览 基本介绍 MATLAB实现BO-GRU贝叶斯优化门控循环单元回归预测。基于贝…...

Easyx趣味编程7,鼠标消息读取及音频播放
hello大家好,这里是dark flame master,今天给大家带来Easyx图形库最后一节功能实现的介绍,前边介绍了绘制各种图形及键盘交互,文字,图片等操作,今天就可以使写出的程序更加生动且容易操控。一起学习吧&…...
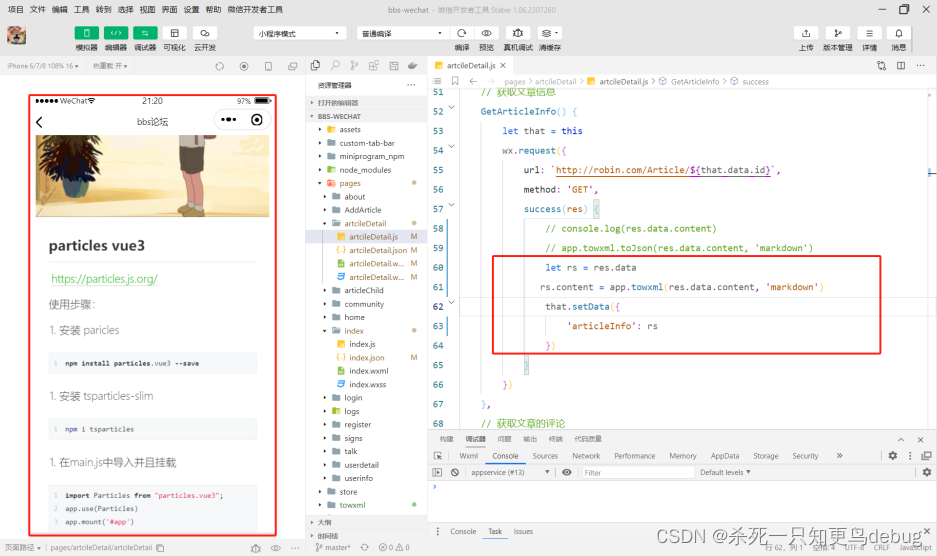
towxml的使用,在微信小程序中快速将markdown格式渲染为wxml文本
towxml的使用,在微信小程序中快速将markdown格式渲染为wxml文本 Towxml概述安装下载 Towxml在小程序中使用 towxml Towxml概述 towxml3.0 支持以下功能: ● echarts图表,默认禁用,需自行构建以开启此功能 ● LaTeX数学公式&#…...
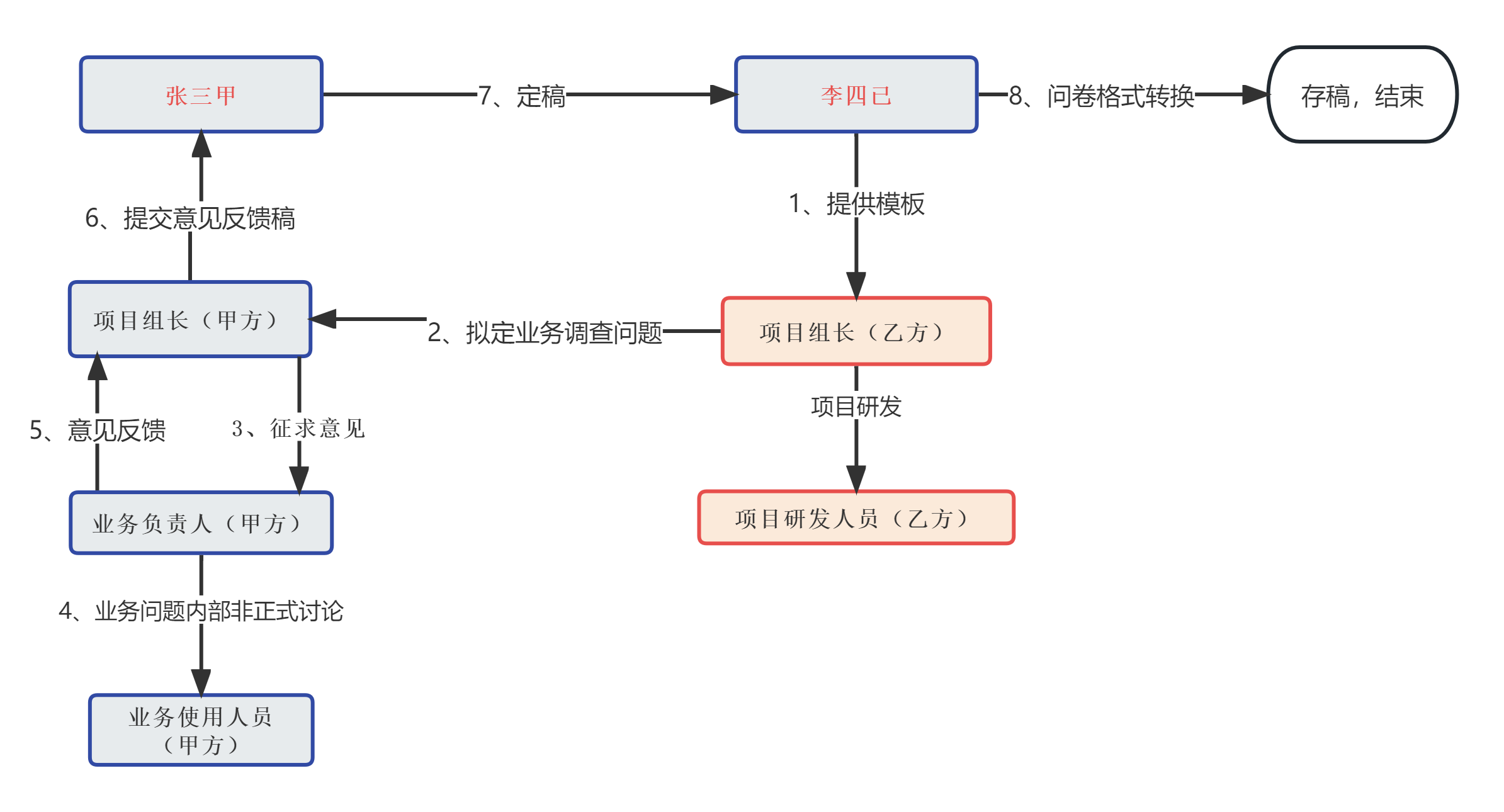
项目管理实战总结(一)-沟通路径问题
前言 那是2021年春节之后,我决定主动申请参与到这个项目,是知道工作强度大、难度大的情况的。有很多的同事是想躲,而我是明知山有虎偏向虎山行。我确定,通过这个项目,一定有我需要的东西。现在项目已经完成了终验专家…...

UE5场景逐渐变亮问题
1、显示 -- 关闭眼部适应 2、项目设置 -- 关闭自动曝光 参考: 虚幻5/UE5 场景亮度逐渐变亮完美解决方法 - 哔哩哔哩...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...
