ESP32C3 LuatOS TM1650①驱动测试
合宙TM1650驱动资料
TM1650.lua源码

引脚连接
| TM1650 | ESP32C3 |
| SCL | GPIO5 |
| SDA | GPIO4 |
下载TM1650.lua源码,并以文件形式保存在项目文件夹中
驱动测试源码
--注意:因使用了sys.wait()所有api需要在协程中使用
-- 用法实例
PROJECT = "ESP32C3_TM1650"
VERSION = "1.0.0"
_G.sys = require("sys")
local tm1650 = require "tm1650"--==========数码管显示例子===========
sys.taskInit(function()--共阴段码表,0~9的数字local NUM_TABLE_AX = {[0]=0x3f,[1]=0x06,[2]=0x5b,[3]=0x4f,[4]=0x66,[5]=0x6d,[6]=0x7d,[7]=0x07,[8]=0x7f,[9]=0x6f}; tm1650.init(5,4,tm1650.MODE_LED_OUTPUT)while 1 dofor i = tm1650.DIG1, tm1650.DIG4, 1 dotm1650.print(i,NUM_TABLE_AX[8])sys.wait(500)endsys.wait(1000)for i = tm1650.BRIGHT1, tm1650.BRIGHT8, 1 dotm1650.setBright(i)sys.wait(500)endfor i = 1, 8, 1 dosys.wait(500)tm1650.close() sys.wait(500)tm1650.open()endsys.wait(2000)tm1650.clear()end
end)sys.run()工程结构

相关文章:

ESP32C3 LuatOS TM1650①驱动测试
合宙TM1650驱动资料 TM1650.lua源码 引脚连接 TM1650ESP32C3SCLGPIO5SDAGPIO4 下载TM1650.lua源码,并以文件形式保存在项目文件夹中 驱动测试源码 --注意:因使用了sys.wait()所有api需要在协程中使用 -- 用法实例 PROJECT "ESP32C3_TM1650" VERSION …...

TCP为什么需要三次握手和四次挥手?
一、三次握手 三次握手(Three-way Handshake)其实就是指建立一个TCP连接时,需要客户端和服务器总共发送3个包 主要作用就是为了确认双方的接收能力和发送能力是否正常、指定自己的初始化序列号为后面的可靠性传送做准备 过程如下ÿ…...
【C++】一些C++11特性
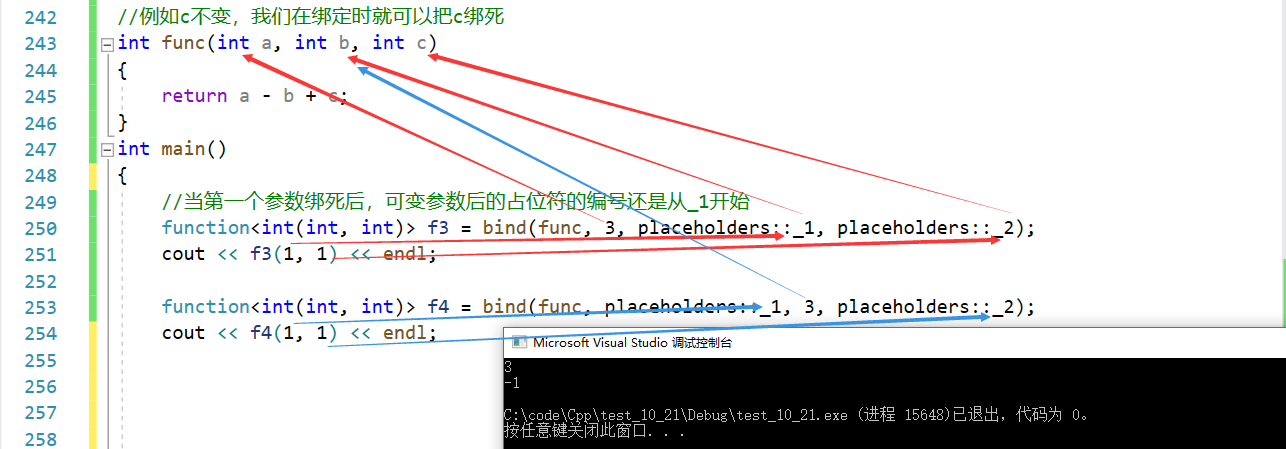
C特性 1. 列表初始化1.1 {}初始化1.2 initializer_list 2. 声明2.1 auto2.2 typeid2.3 decltype2.4 nullptr 3. STL3.1 新容器3.2 新接口 4. 右值引用5. 移动构造与移动赋值6. lambda表达式7. 可变参数模板8. 包装器9. bind 1. 列表初始化 1.1 {}初始化 C11支持所有内置类型和…...

leetcode 647. 回文子串、516. 最长回文子序列
647. 回文子串 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串,即使是由相同的字符组成&#…...

Vue Router 刷新当前页面
Vue项目, 在实际工作中, 有些时候需要在 加载完某些数据之后对当前页面进行刷新, 以期 onMounted 等生命周期函数, 或者 数据重新加载. 总之是期望页面可以重新加载一次. 目前总结有三种途径可实现以上需求: 一, reload 直接刷新页面 window.location.reload(); $router.go(…...

lstm 回归实战、 分类demo
预备知识 lstm 参数 输入、输出格式 nn.LSTM(input_dim,hidden_dim,num_layers); imput_dim 特征数 input:(样本数、seq, features_num) h0,c0 (num_layers,seq, hidden_num) output: (样本数、seq, hidden_dim) 再加一个全连接层,将 outpu…...

实践DDD模拟电商系统总结
目录 一、事件风暴 二、系统用例 三、领域上下文 四、架构设计 (一)六边形架构 (二)系统分层 五、系统实现 (一)项目结构 (二)提交订单功能实现 (三࿰…...
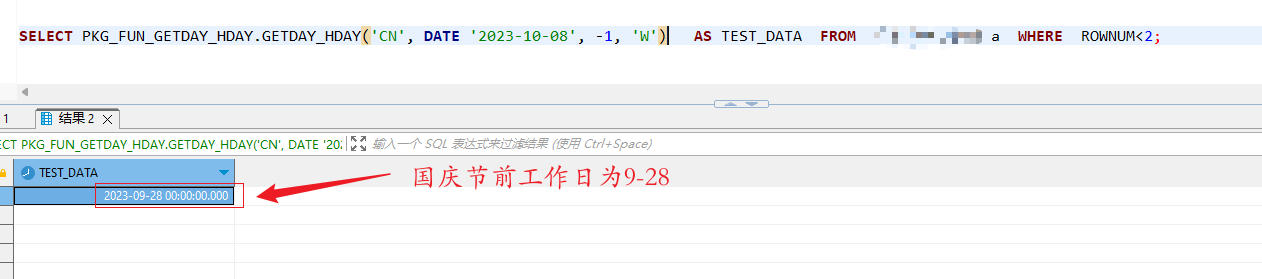
`SQL`编写判断是否为工作日函数编写
SQL编写判断是否为工作日函数编写 最近的自己在写一些功能,遇到了对于工作日的判断,我就看了看sql,来吧!~(最近就是好疲惫) 我们一起看看(针对ORACLE) 1.声明: CREATE OR REPLACE PACKAGE GZYW_2109_1214.PKG_FUN_GETDAY_HDAY AS /** * 通过节假日代码获取指定的日期[查找基…...
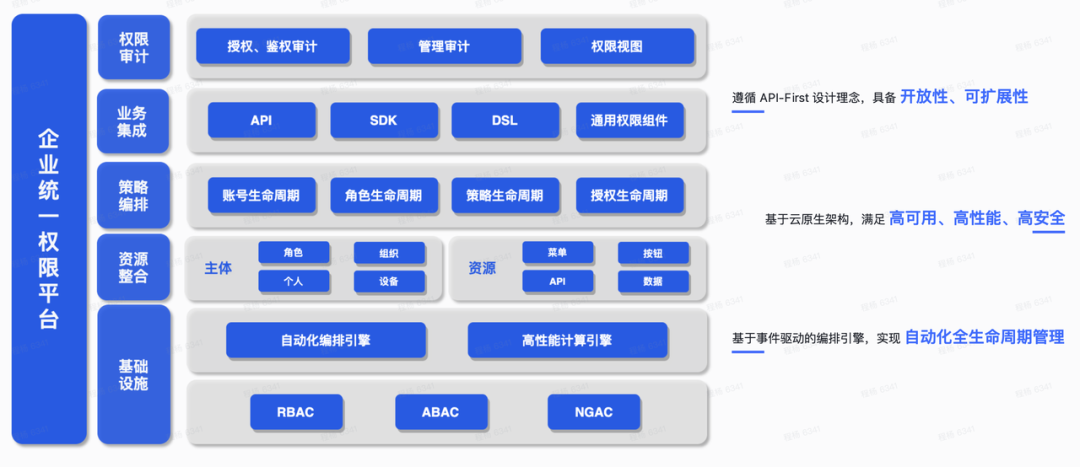
零信任身份管理平台,构建下一代网络安全体系
随着数字化时代的到来,网络安全已成为企业和组织面临的一项重要挑战。传统的网络安全方法已经无法满足不断演变的威胁和技术环境。近期,中国信息通信研究院(简称“中国信通院”)发布了《零信任发展研究报告( 2023 年&a…...

《数据结构、算法与应用C++语言描述》使用C++语言实现链表队列
《数据结构、算法与应用C语言描述》使用C语言实现链表队列 定义 队列的定义 队列(queue)是一个线性表,其插入和删除操作分别在表的不同端进行。插入元素的那一端称为队尾(back或rear),删除元素的那一端称…...
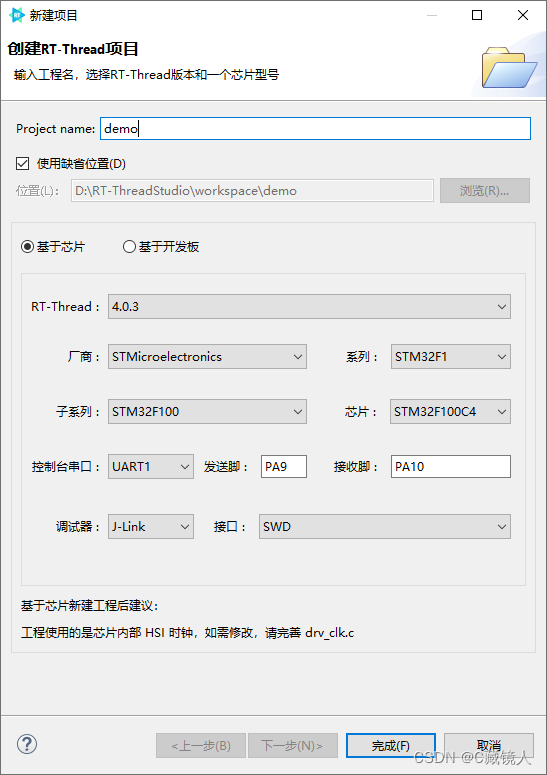
RT-Thread学习笔记(四):RT-Thread Studio工具使用
RT-Thread Studio工具使用 官网详细资料实用操作1. 查看 RT-Thread RTOS API 文档2.打开已创建的工程3.添加头文件路径4. 如何设置生成hex文件5.新建工程 官网详细资料 RT-Thread Studio 用户手册 实用操作 1. 查看 RT-Thread RTOS API 文档 2.打开已创建的工程 如果打开项目…...
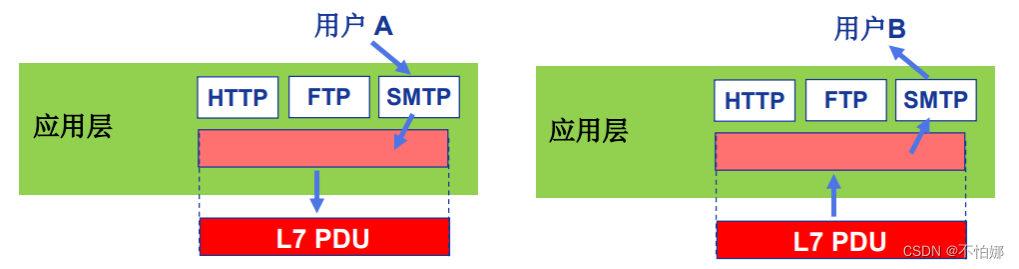
【计算机网络笔记】OSI参考模型中端-端层(传输层、会话层、表示层、应用层)功能介绍
系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 数据交换之报文交换和分组交换 分组交换 vs 电路交换 计算机网络性能(1)——速率、带宽、延迟 计算机网络性能(2)…...

RabbitMQ高级知识点
以下是一些 RabbitMQ 的高级知识点: 1. Exchange: RabbitMQ 中的 Exchange 是消息路由器,用来接收消息并且转发到对应的 Queue 中。Exchange 有四种类型:Direct Exchange、Fanout Exchange、Topic Exchange 和 Headers Exchange。…...

Node直接执行ts文件
Node直接执行ts文件 1、常规流程 node 执行 【ts 文件】 流程: 1、编写ts代码 2、编译成js代码 [命令如 :tsc xx.ts] 3、执行js代码 [node xx.js]2、直接执行 想要直接执行 ts 文件,需要安装如下依赖工具。 执行如下命令: # 安装…...

log4j的级别的说明
一 log4j的级别 1.1 级别类型 TRACE 》DEBUG 》 INFO 》 WARN 》 ERROR 》 FATAL 级别高低顺序为: trace级别最低 ,Fatal级别最高。由左到右,从低到高 1.2 包含范围 原则: 本级别包含本级别以及大于本级别的内容,…...

头脑风暴之约瑟夫环问题
一 问题的引入 约瑟夫问题的源头完全可以命名为“自杀游戏”。本着和谐友爱和追求本质的目的,可以把问题描述如下: 现有n个人围成一桌坐下,编号从1到n,从编号为1的人开始报数。报数也从1开始,报到m人离席,…...
【四:Spring整合Junit】
目录 相同点不同点1、导入依赖增加2、编写的位置不同。。路径一定要与实现类一致 相同点 前面都一样和Spring整合mybatis(基于注解形式)一样Spring整合Mybatis 不同点 1、导入依赖增加 <!-- 单元测试 --><dependency><groupId>junit&…...
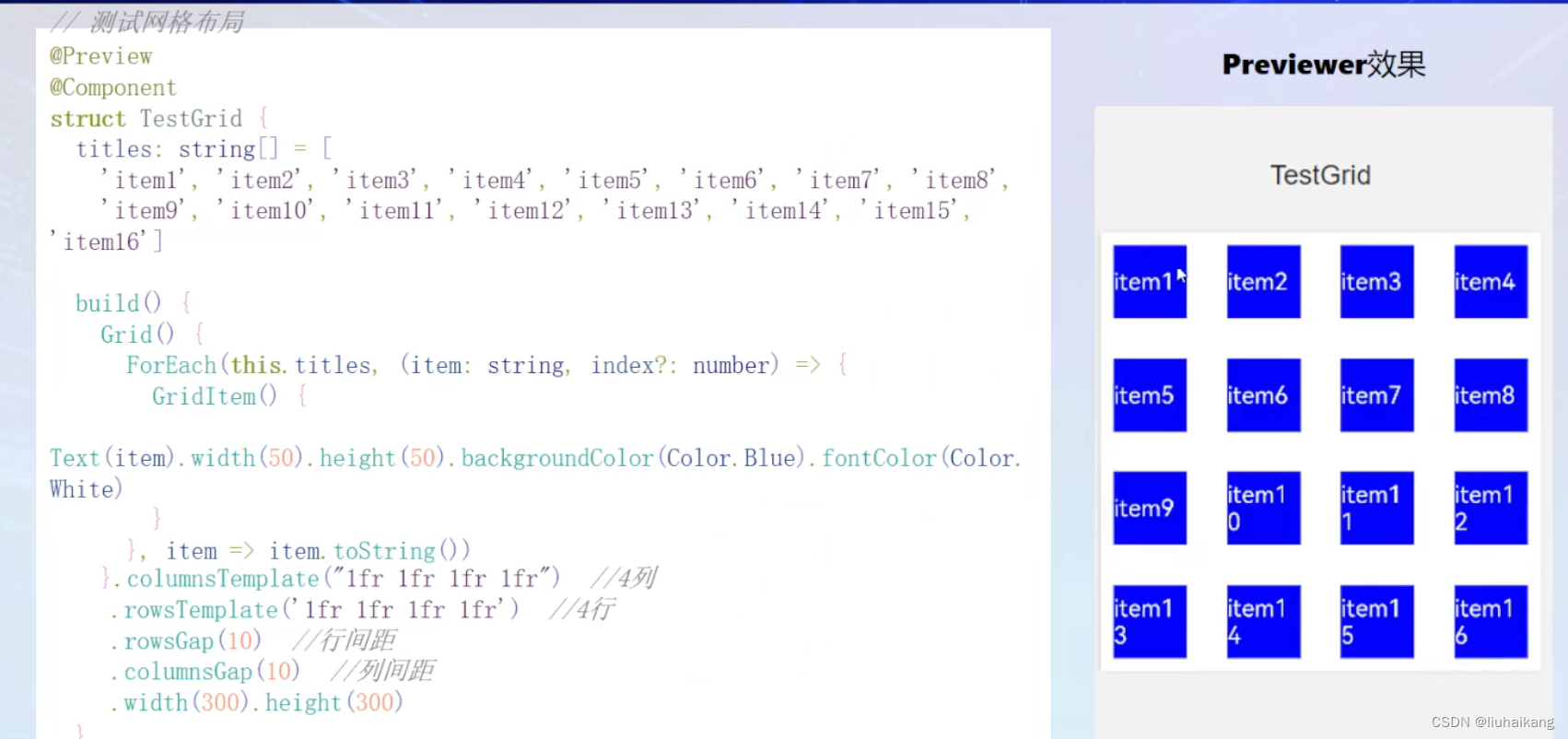
openHarmony UI开发
常用组件和布局方式 组件 ArkUI有丰富的内置组件,包括文本、按钮、图片、进度条、输入框、单选框、多选框等。和布局一样,我们也可以将基础组件组合起来,形成自定义组件。 按钮: Button(Ok, { type: ButtonType.Normal, stateEf…...
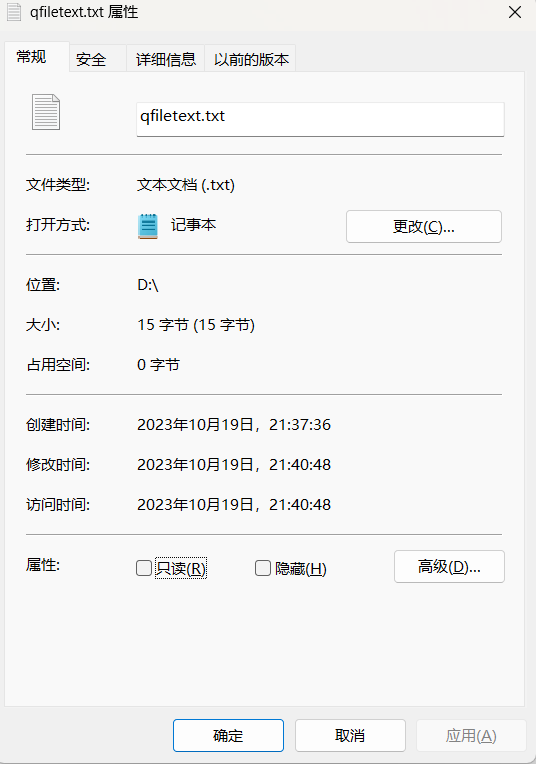
Qt 目录操作(QDir 类)及展示系统文件实战 QFilelnfo 类介绍和获取文件属性项目实战
一、目录操作(QDir 类) QDir 类提供访问系统目录结构 QDir 类提供对目录结构及其内容的访问。QDir 用于操作路径名、访问有关路径和文件的信息以及操作底层文件系统。它还可以用于访问 Qt 的资源系统 Qt 使用“/”作为通用目录分隔符,与“/”在 URL 中用作路径分…...

2023-9-12 阿里健康2024秋招后端开发-体检及泛医疗二面
1 自我介绍 2 快手实习 2.1 说说你在实习期间遇到的挑战、收获 (1)在设计模式的应用能力上,有了很大的提高,使用模板设计模式,架构实例反向同步到架构定义,使用了策略模式 (2) …...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...
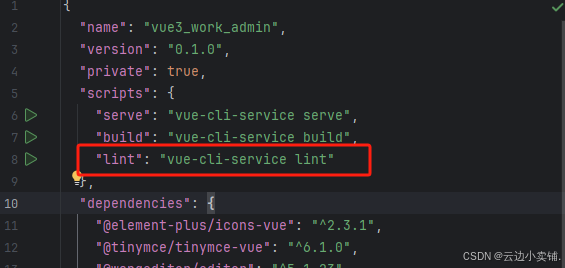
运行vue项目报错 errors and 0 warnings potentially fixable with the `--fix` option.
报错 找到package.json文件 找到这个修改成 "lint": "eslint --fix --ext .js,.vue src" 为elsint有配置结尾换行符,最后运行:npm run lint --fix...

基于谷歌ADK的 智能产品推荐系统(2): 模块功能详解
在我的上一篇博客:基于谷歌ADK的 智能产品推荐系统(1): 功能简介-CSDN博客 中我们介绍了个性化购物 Agent 项目,该项目展示了一个强大的框架,旨在模拟和实现在线购物环境中的智能导购。它不仅仅是一个简单的聊天机器人,更是一个集…...
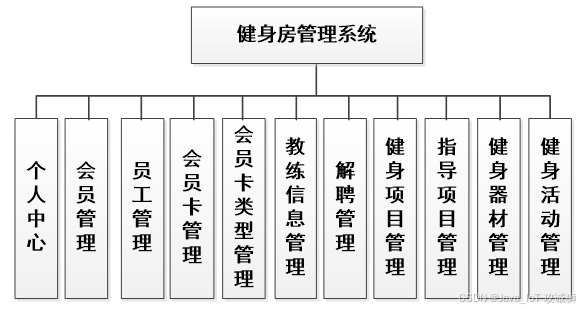
基于django+vue的健身房管理系统-vue
开发语言:Python框架:djangoPython版本:python3.8数据库:mysql 5.7数据库工具:Navicat12开发软件:PyCharm 系统展示 会员信息管理 员工信息管理 会员卡类型管理 健身项目管理 会员卡管理 摘要 健身房管理…...

PostgreSQL 对 IPv6 的支持情况
PostgreSQL 对 IPv6 的支持情况 PostgreSQL 全面支持 IPv6 网络协议,包括连接、存储和操作 IPv6 地址。以下是详细说明: 一、网络连接支持 1. 监听 IPv6 连接 在 postgresql.conf 中配置: listen_addresses 0.0.0.0,:: # 监听所有IPv4…...
