失配树学习笔记
失配树,是一种奇妙的数据结构,它利用 KMP、LCA 解决求两前缀的最长公共 Border 的问题。
首先介绍一下什么是 Border,我们知道 nxt 数组是前后缀相同的最大长度,Border 相当于是 nxt 数组的弱化版,只是去掉了“最大”的限制。
我们考虑如何建立一棵失配树(fail 树),对于每一个长度为 i i i 的前缀,我们预处理出它的 nxt,然后按照 i i i 指向 nxt[i],即 nxt[i] 是 i i i 的爹。
对于两个前缀的最长 Border,我们只需要对于两个区间的 i i i、 j j j 求出它们的 LCA 即可。这里需要注意一个坑,如果 i i i 和 j j j 的 LCA 是他们中的一个,那么我们要把 LCA 上提一步,即返回 f[i][0] 或 f[j][0](返回他们的父亲)。
练手板子题
代码如下:
#include <bits/stdc++.h>
using namespace std;const int maxn=1e6+5;
char s[maxn];
int f[maxn][25],dep[maxn];int lca(int x,int y)
{if(dep[x]<dep[y]) swap(x,y);for(int i=20;i>=0;i--) if(dep[f[x][i]]>=dep[y]) x=f[x][i];if(x==y) return f[x][0];for(int i=20;i>=0;i--)if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];return f[x][0];
}int main()
{scanf("%s",s+1);int len=strlen(s+1);f[0][0]=f[1][0]=0;dep[0]=0;dep[1]=1;for(int i=1,j=0;i<=len;i++){while(j&&s[i+1]!=s[j+1]) j=f[j][0];if(s[i+1]==s[j+1]) j++;f[i+1][0]=j,dep[i+1]=dep[j]+1;}int m;cin>>m;for(int j=1;j<=20;j++) for(int i=1;i<=len;i++) f[i][j]=f[f[i][j-1]][j-1];while(m--){int p,q;cin>>p>>q;cout<<lca(p,q)<<endl;}return 0;
}
相关文章:

失配树学习笔记
失配树,是一种奇妙的数据结构,它利用 KMP、LCA 解决求两前缀的最长公共 Border 的问题。 首先介绍一下什么是 Border,我们知道 nxt 数组是前后缀相同的最大长度,Border 相当于是 nxt 数组的弱化版,只是去掉了“最大”…...

【Electron】Not allowed to load local resource
问题描述 使用 audio 标签播放音频文件,控制台报错 Not allowed to load local resource。 Not allowed to load local resource原因分析 通常是安全策略所引起的。Electron 默认情况下禁止加载本地资源,以防止潜在的安全风险。 解决方案 在 main.js…...

Maven 基础教程系列
Maven是一个项目开发管理和理解工具。基于项目对象模型的概念:构建、依赖关系管理、文档创建、站点发布和分发发布都由pom.xml声明性文件控制。Maven可以通过插件进行扩展,以使用许多其他开发工具来报告或构建过程。 一、Maven 使用教程-CSDN博客 二、…...

c++之类和对象
1.auto 可以自动推导结果的类型 typeid()可以打印类型 引用也可以 auto真正的价值可以简化迭代器的写法 并且auto定义的变量必须初始化。 不能做参数 返回值也不可以用auto auto不能用来声明数组 如果想要修改要用引用且指针不好解决。 c11之后的nullptr 以后再用空指针用nul…...
分布式应用开发的核心技术系列之——基于TCP/IP的原始消息设计
本文由葡萄城技术团队原创并首发。转载请注明出处:葡萄城官网,葡萄城为开发者提供专业的开发工具、解决方案和服务,赋能开发者。 前言 本文的内容主要围绕以下几个部分: TCP/IP的简单介绍。消息的介绍。基于消息分类的传输格式&…...

医疗领域的数字化浪潮:互联网医院平台的关键作用
数字化浪潮正在迅速改变医疗领域的方式和效率。互联网医院平台作为数字化医疗的关键元素,正在为医疗行业带来巨大的变革。本文将探讨互联网医院平台的关键作用,并提供一个示例,使用Python编写一个简单的医疗预约系统。 互联网医院平台的关键…...
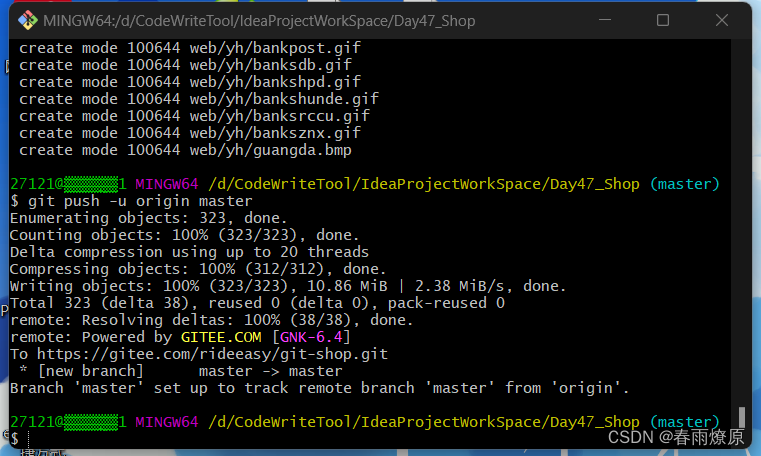
将本地的项目上传到Gitee
目录 1.先在Gitee新建一个仓库,提交即可 2.进入到要上传的项目里面,右键选择 Git Bash Here 3.右键后就打开了Git命令窗口 4.配置你的用户名和邮箱(已经配置过则可跳过) 5.查看你的用户名和邮箱配置(可不查看) 6.输入git init指令&#…...
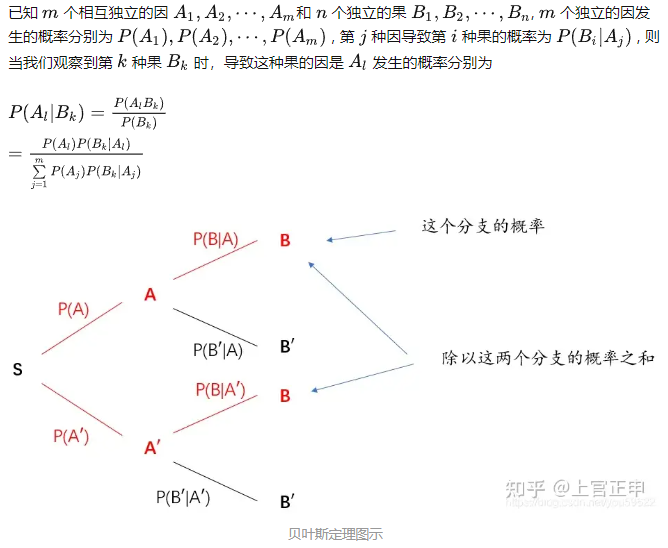
概率论_概率公式中的分号(;)、逗号(,)、竖线(|)
1. 概率公式中的分号(;)、逗号(,)、竖线(|) ; 分号代表前后是两类东西,以概率P(x;θ)为例,分号前面是x样本,分号后边是模型参数。 , 逗号代表两者地位平等,代表与的关系 | 竖线代表 if,一上面为例,就是如果…...

Spark Streaming 整合 Kafka
本文代码链接:https://download.csdn.net/download/shangjg03/88442308 1.版本说明 Spark 针对 Kafka 的不同版本,提供了两套整合方案:`spark-streaming-kafka-0-8` 和 `spark-streaming-kafka-0-10`,其主要区别如下: 本文使用的 Kafka 版本为 `kafka_2.12-2.2.0`,故采用…...
【API篇】五、Flink分流合流API
文章目录 1、filter算子实现分流2、分流:使用侧输出流3、合流:union4、合流:connect5、connect案例 分流,很形象的一个词,就像一条大河,遇到岸边有分叉的,而形成了主流和测流。对于数据流也一样…...
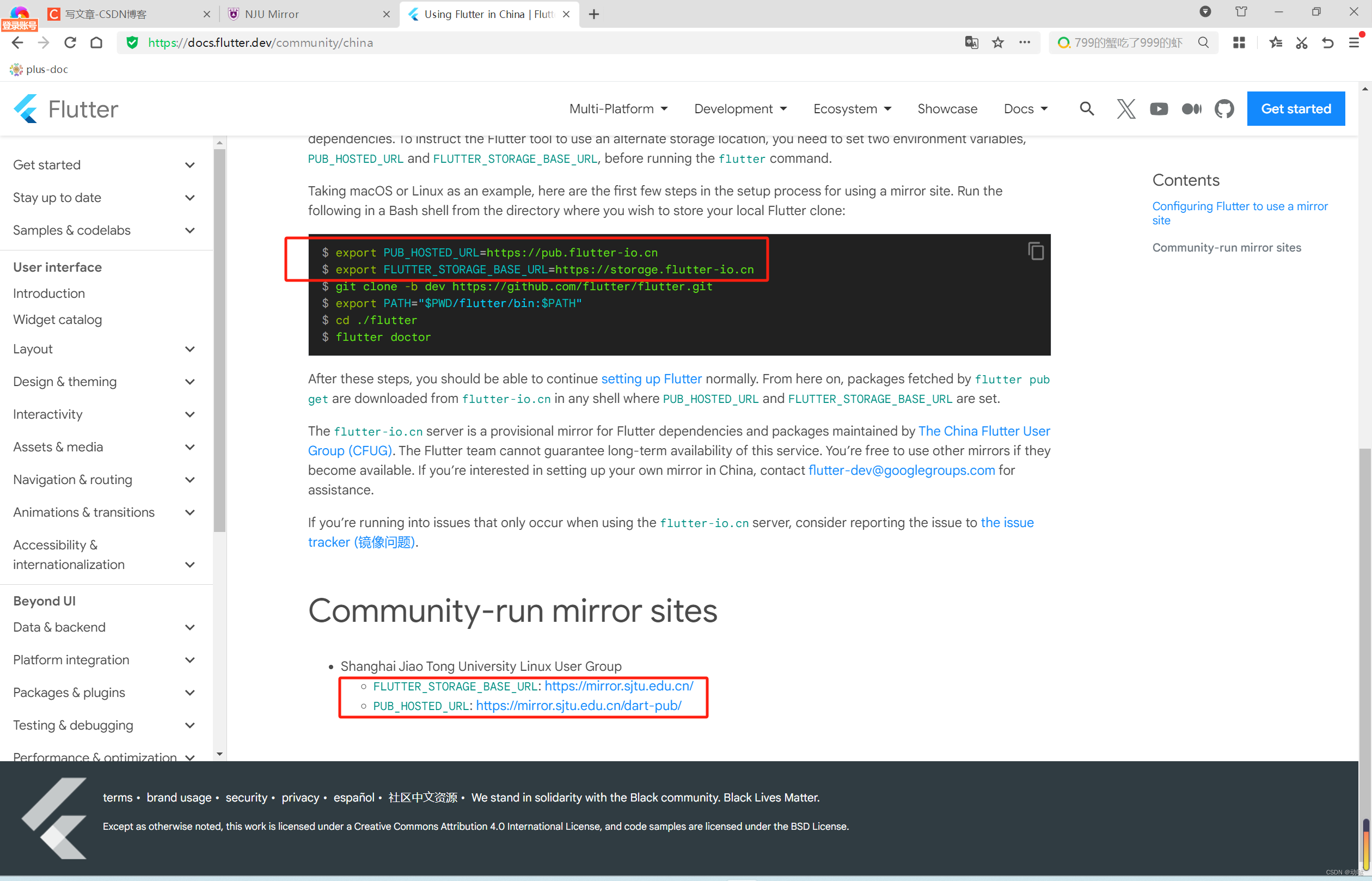
flutter开发的一个小小小问题,内网依赖下不来
问题 由于众所周知的原因,flutter编译时,经常出现Could not get resource https://storage.googleapis.com/download.flutter.io…的问题,如下: * What went wrong: Could not determine the dependencies of task :app:lintVit…...
RabbitMQ队列及交换机的使用
目录 一、简单模型 1、首先控制台创建一个队列 2、父工程导入依赖 3、生产者配置文件 4、写测试类 5、消费者配置文件 6、消费者接收消息 二、WorkQueues模型 1、在控制台创建一个新的队列 2、生产者生产消息 3、创建两个消费者接收消息 4、能者多劳充分利用每一个消…...

分布式唯一Id,它比GUID好
分布式唯一Id,它比GUID好 一、前言 分布式唯一Id,顾名思义,是指在全世界任何一台计算机上都不会重复的唯一Id。 在单机/单服务器/单数据库的小型应用中,不需要用到这类东西。但在高并发、海量数据、大型分布式应用中,…...

计算机服务器中了勒索病毒怎么解决,勒索病毒解密流程,数据恢复
计算机服务器中了勒索病毒是一件非常令人头疼的事情,勒索病毒不仅会加密企业服务器中的数据,还会对企业计算机系统带来损害,严重地影响了企业的正常运转。最近,云天数据恢复中心工程师总结了,今年以来网络上流行的勒索…...

【NPM】vuex 数据持久化库 vuex-persistedstate
在 GitHub 上找到:vuex-persistedstate。 安装 npm install --save vuex-persistedstate使用 import { createStore } from "vuex"; import createPersistedState from "vuex-persistedstate";const store createStore({// ...plugins: [cr…...

英语——分享篇——每日200词——2601-2800
2601——resistant——[rɪzɪstənt]——adj.抵抗的——resistant——resi热死(拼音)st石头(拼音)ant蚂蚁(熟词)——热死了石头上的蚂蚁还在抵抗——The body may be less resistant if it is cold. ——天冷时,身体的抵抗力会下降。 2602——prospect——[prɒspe…...

SpringCloud-Sentinel
一、介绍 (1)提供界面配置配置服务限流、服务降级、服务熔断 (2)SentinelResource的blockHandler只处理后台配置的异常,运行时异常fallBack处理,且资源名为value时才生效,走兜底方法 二、安装…...
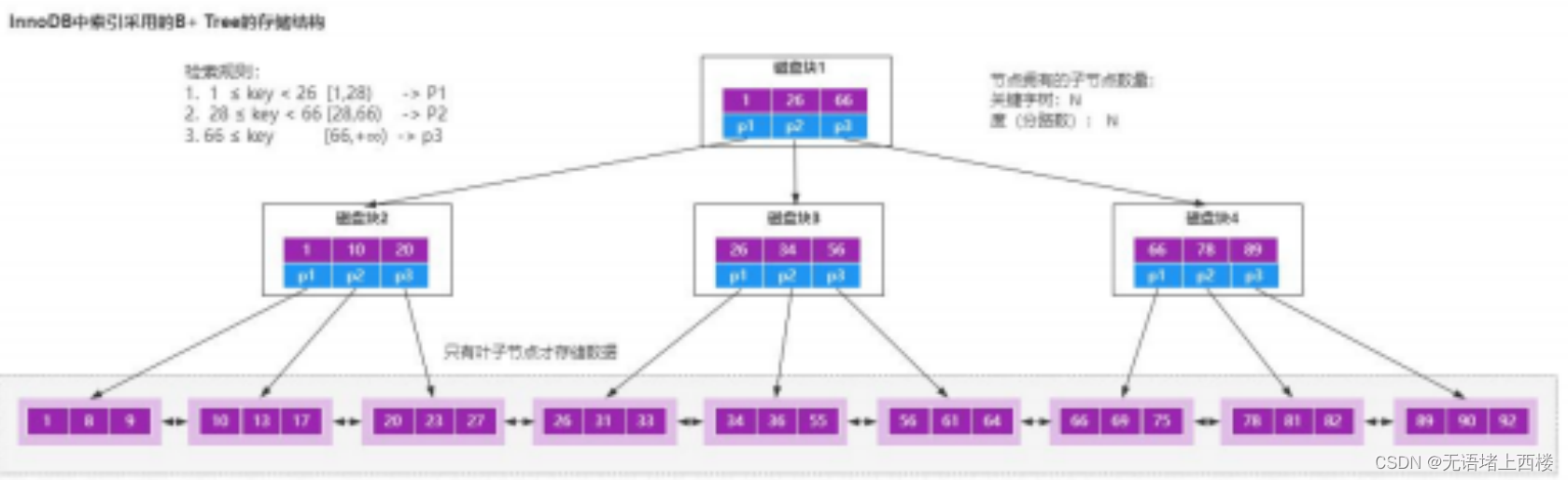
为什么索引要用B+树来实现呢,而不是B树
首先,常规的数据库存储引擎,一般都是采用 B 树或者 B树来实现索引的存储。 B树 因为 B 树是一种多路平衡树,用这种存储结构来存储大量数据,它的整个高度会相比二叉树来说,会矮很多。 而对于数据库来说,所有…...

使用vue3前端开发的一些知识点
Vue 3 是一种流行的 JavaScript 框架,用于构建用户界面。它是 Vue.js 框架的第三个主要版本,具有许多新特性和性能改进。下面是 Vue 3 的一些常用语法和概念的详细介绍: 创建 Vue 实例: 在 Vue 3 中,你可以通过创建一个…...
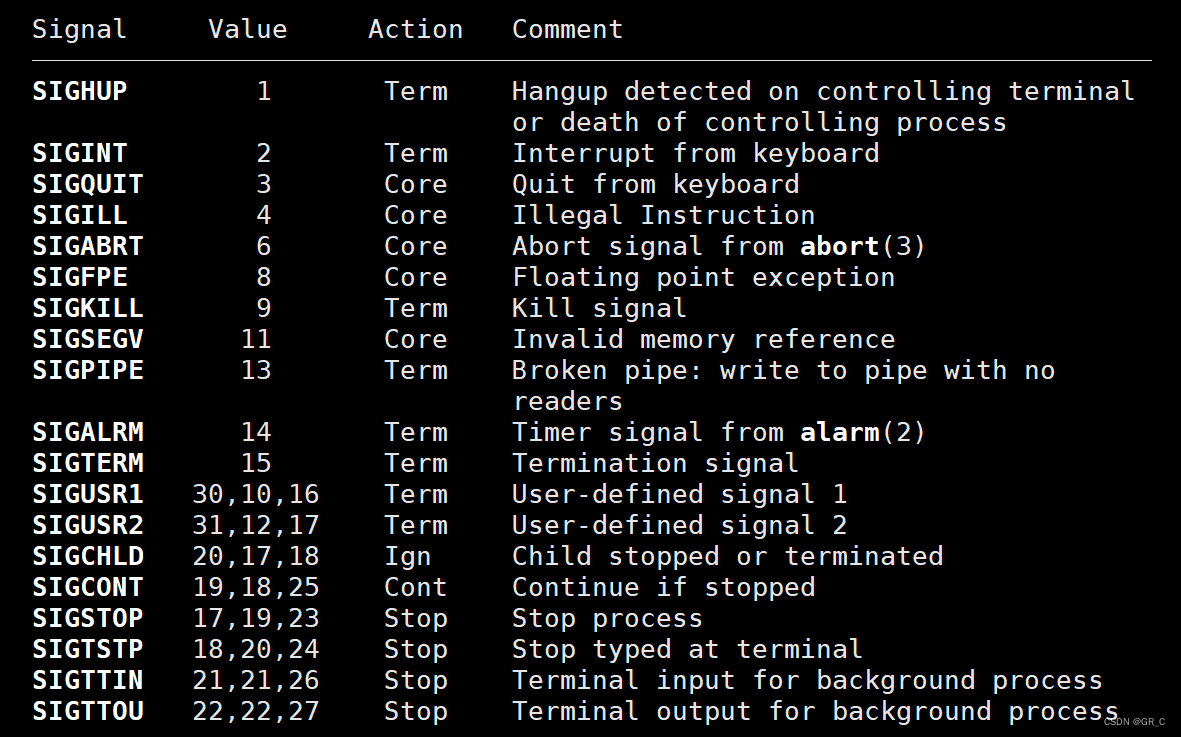
零基础Linux_20(进程信号)内核态和用户态+处理信号+不可重入函数+volatile
目录 1. 内核态和用户态 1.1 内核态和用户态概念 1.2 内核态和用户态转化 2. 处理信号 2.2 捕捉信号 2.2 系统调用sigaction 3. 不可重入函数 4. volatile关键字 5. SIGCHLD信号(了解) 6. 笔试选择题 答案及解析 本篇完。 1. 内核态和用户态…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
