DP基础相关笔记
基础 DP
LIS
LIS(Longest Increasing Subsequence),顾名思义,就是最长上升子序列问题。
在这里我们要区分一下子串和子序列的区别,很简单,子串连续,子序列可以不连续。然而就在几小时之前本蒟蒻还不知道
简单来说,就是给出一个内容不重复的序列,求它的最长上升子序列。听君一席话,如听一席话
下面介绍两种做法, O ( n 2 ) O(n^2) O(n2) 的 DP 做法和 O ( n log n ) O(n\log n) O(nlogn) 的二分做法。
O ( n 2 ) O(n^2) O(n2) DP
我们用 dp[i] 表示以 a[i] 为结尾的 LIS,剩下的自己理解就好啦 QwQ 学了优化之后就不会朴素做法了
#include <bits/stdc++.h>
using namespace std;const int maxn=105,inf=0x7f7f7f7f;
int a[maxn],dp[maxn],n,ans=-inf;int main()
{cin>>n;for(int i=1;i<=n;i++)cin>>a[i],dp[i]=1;for(int i=1;i<=n;i++)for(int j=1;j<i;j++)if(a[j]<a[i])dp[i]=max(dp[i],dp[j]+1);for(int i=1;i<=n;i++) ans=max(ans,dp[i]);cout<<ans;return 0;
}
O ( n log n ) O(n\log n) O(nlogn) 二分
显然,对于一个 LIS,要让它结尾的数尽量的小,才能使LIS最长。
举个栗子:对于“ 5201314 \texttt{5201314} 5201314”,第一步为“ 5 \texttt{5} 5”;第二步发现 2 < 5 2<5 2<5,所以换为“ 2 \texttt{2} 2”;第三步发现 0 < 2 0<2 0<2,所以换为“ 0 \texttt{0} 0”;第四步发现 1 > 0 1>0 1>0,把 1 1 1放进去变为“ 05 \texttt{05} 05”;第五步发现 0 < 3 < 5 0<3<5 0<3<5,所以换为“ 03 \texttt{03} 03”,以此类推。
对于这个的实现,我们可以巧妙地运用 lower_bound 函数进行二分查找,查找这个要放进去的值所在的区间。
代码如下:
#include <bits/stdc++.h>
using namespace std;int a[105],f[105];//f is LISint main()
{int n;cin>>n;for(int i=1;i<=n;i++) cin>>a[i];f[1]=a[1];int len=1;for(int i=2;i<=n;i++){if(a[i]>f[len]) len++,f[len]=a[i];else{int j=lower_bound(f+1,f+n+1,a[i])-f;f[j]=a[i];}}cout<<len;return 0;
}
发现自己真的是鱼,差点没写出来
LCS
LCS(Longest Common Sequence),顾名思义,就是最长公共子序列问题。
同样的,还是有两种不同时间复杂度的做法,一种 O ( n 2 ) O(n^2) O(n2),一种 O ( n log n ) O(n\log n) O(nlogn)。
O ( n 2 ) O(n^2) O(n2) DP
假设 dp ( i , j ) \operatorname{dp}(i,j) dp(i,j) 为序列 A = a 1 a 2 ⋯ a i A=a_1a_2\cdots a_i A=a1a2⋯ai 与序列 B = b 1 b 2 ⋯ B j B=b_1b_2\cdots B_j B=b1b2⋯Bj 的最长公共子序列的长度。当 i = 0 i=0 i=0 或 j = 0 j=0 j=0 时,空序列是 A A A、 B B B 序列的最长子序列,状态转移方程如下:
d p ( i , j ) = { 0 i = 0 ∨ j = 0 d p ( i − 1 , j − 1 ) + 1 i , j > 0 , x i = y j max ( d p ( i , j − 1 ) , d p ( i − 1 , j ) ) x i ≠ y j dp(i,j)= \begin{cases}0&i=0\vee j=0\\\\ dp(i-1,j-1)+1&i,j>0,x_i=y_j\\\\ \max(dp(i,j-1),dp(i-1,j))&x_i\neq y_j \end{cases} dp(i,j)=⎩ ⎨ ⎧0dp(i−1,j−1)+1max(dp(i,j−1),dp(i−1,j))i=0∨j=0i,j>0,xi=yjxi=yj
O ( n log n ) O(n\log n) O(nlogn) 二分
我们可以建立一个映射,把序列 A A A 中的每一个元素映射为它对应的数组下标(这里本可以用 map 炫技,但是我们还是采用朴素的数组实现),显然这个序列是上升的,我们把 B B B 中可以转换的元素都转换为它在 A A A 中的数组下标,由于要满足递增才能保证序列公共,所以我们就把问题转化成了一个 LIS 问题。
代码如下:
#include <bits/stdc++.h>
using namespace std;
int a[100005],b[100005],c[100005],dp[100005],mp[100005];
int main()
{int n;cin>>n;for(int i=1;i<=n;i++) cin>>a[i],mp[a[i]]=i;for(int i=1;i<=n;i++) scanf("%d",&b[i]);for(int i=1;i<=n;i++)c[i]=mp[b[i]];//c存储公共子序列int temp=0,ans=-0x7fffffff;for(int i=1;i <= n;i++){int j=upper_bound(dp+1,dp+temp+1,c[i])-dp;if(j==temp+1) temp++,dp[j]=c[i];else dp[j]=c[i];}cout<<temp;return 0;
}
状压 DP
状压 DP 的特点:
- 数据规模的某一维或几维很小
- 最优性原理
- 无后效性
状压 DP 的灵魂就是位运算和二进制,可以复习一下 qwq。
详见 P1896题解。
状压 DP 位运算技巧,转载自 Xu brezza,原文链接
询问第 i i i 位是否为 1 1 1:
x&(1<<(i-1))
- 如果这么写返回的不是 1 1 1 !
(x>>(i-1))&1
- 这样才返回 01 01 01
将 x x x 第 i i i 位取反
x^=1<<(i-1)将 x x x 第 i i i 位变为 1 1 1
x|=1<<(i-1)将 x x x 第 i i i 位变为 0 0 0
x&=(~(1<<(i-1)))去掉 x x x 最右边的 1 1 1,也就是 lowbit ( x ) \text{lowbit}(x) lowbit(x)
x&=x-1取出最右边的 1 1 1 ,还是 lowbit ( x ) \text{lowbit}(x) lowbit(x)
x&(-x)判断是否有连续的 1 1 1
x&(x<<1)还是注意,不返回 1 1 1。
- 枚举子集
敲黑板,非常重要且实用!
for(int y=x;y;y=(y-1)&x)
数位 DP
数位 DP,顾名思义,就是针对数位的 DP。
举个栗子,求给定区间中,满足给定条件的,某个进制数或此类数的数量。给定条件通常与数位有关,例如数位之和、指定数码个数、数的大小顺序分组等。邪恶的出题人往往把区间开的很大,让我们的暴力解法无法实现,所以我们就需要采用数位 DP 解决。
数位 DP 的基本思想:逐位确定。
练手板子题:P2657
区间 DP
区间类动态规划问题,首先考虑的就是建立一个数组 f ( i , j ) f(i,j) f(i,j) 存储区间内的最优解,然后枚举断点 k k k, f ( i , j ) = f ( i , k ) + f ( k + 1 , j ) f(i,j)=f(i,k)+f(k+1,j) f(i,j)=f(i,k)+f(k+1,j)。
区间 DP 的解法基本满足:
- 枚举区间
- 枚举左端点
- 枚举断点
区间DP的特点:
- 合并:合并区间或拆分区间
- 特征:能将问题转化为区间合并
- 求解:类似分治
区间DP有一种特殊情况,即环状区间,我们可以把一个长为 n n n 的环转化为 2 n 2n 2n 长的链,枚举 f ( 1 , n ) , f ( 2 , n + 1 ) , ⋯ , f ( n , 2 n − 1 ) f(1,n),f(2,n+1),\cdots,f(n,2n-1) f(1,n),f(2,n+1),⋯,f(n,2n−1) 找到最优值即可。
树形 DP(树上背包)
对于一棵树,每个节点上有一个物品,每个体积为 w i w_i wi,价值为 v i v_i vi。选了一个点必须选它的父亲。问总体积不超过 m m m 的情况下总价值最大值。
乍一看,很像一道 01 01 01 背包,但是又有基于树状数据结构的限制条件。
于是乎,我们请出神级 DP 状态设计。
首先我们来一种更加好懂的三维思路。我们设 f ( i , j , k ) f(i,j,k) f(i,j,k) 表示对于根节点为 i i i 的子树,考虑它的前 k k k 棵子树,给它 j j j 的体积,能得到的最大价值。显然这时候, i i i 物品一定要选。显然,当前状态一定是由前 k − 1 k-1 k−1 棵子树转移而来,于是乎我们可以用 01 01 01 背包的思想压掉一维。
常见状态转移方程:(注意由于要考虑儿子的状态,所以要先 DFS)
void dfs(int x)
{f[x][1]=val[x];for(int i=head[x];i;i=nxt[i]){dfs(to[i]);for(int j=M+1;j;j--)for(int k=1;k<j;k++)f[x][j]=max(f[x][j],f[to[i]][k]+f[x][j-k]);}
}
树上背包的时间复杂度证明(来自大佬 @Steven24):

相关文章:

DP基础相关笔记
基础 DP LIS LIS(Longest Increasing Subsequence),顾名思义,就是最长上升子序列问题。 在这里我们要区分一下子串和子序列的区别,很简单,子串连续,子序列可以不连续。然而就在几小时之前本蒟…...
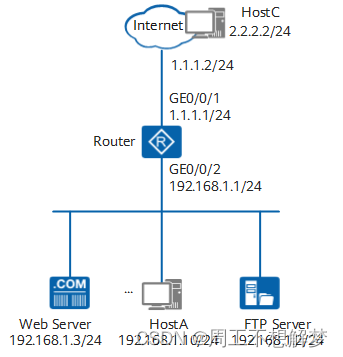
配置公网和私网用户通过非公网口的IP地址访问内部服务器和Internet示例
组网需求 如配置公网和私网用户通过非公网口的IP地址访问内部服务器和Internet示例所示,某小型企业内网部署了一台路由器、一台FTP服务器和一台Web服务器。路由器作为接入网关,为下挂的内网用户提供上网服务,主要包括浏览网页、使用即时通信…...
相机镜头选择与机器视觉控制
相机镜头选择与机器视觉控制 在机器视觉领域,除了图像处理和算法,还需要关注硬件方面的选型和控制。相机镜头的选择是其中重要的一部分,需要考虑像素大小、镜头焦距等因素以满足项目需求。此外,编程技能也包括相机的调用和使用&a…...

Git 为文件添加执行权限
背景 当你是一台Linux,想要给文件加权限很简单,只需要执行以下命令 chmod x filename就可以给文件添加执行权限,但是如果你是Windows那就很麻烦了 解决方案 假设这里有一个名为 file.sh 的文件,内容如下: #!/bin/…...

问题记录:GPU显卡提高后,代码总体运行效率没有提高
问题:GPU显卡提高后,代码总体运行效率没有提高 原先显卡NIVIDA T400换成NVIDIA RTX A4000,CUDA核心(物理GPU线程单位)从三百多提升到了六千多,但是程序总体运行的时间没有变化。 原因分析 显卡没用上或者…...

Reparameterization trick(重参数化技巧)
“Reparameterization trick”(重参数化技巧)是一种在训练生成模型中处理随机性潜在变量的方法,特别常见于变分自动编码器(VAE)等模型中。这个技巧的目的是使模型可微分(differentiable)&#x…...

Kotlin中的可空类型
在 Kotlin 中,可空类型是一项重要的特性,它允许我们声明变量可以为空。在本篇博客中,我们将介绍 Kotlin 中的可空类型,并提供示例代码演示如何处理可空变量、使用安全调用操作符(?.)、Elvis 运算符&#x…...
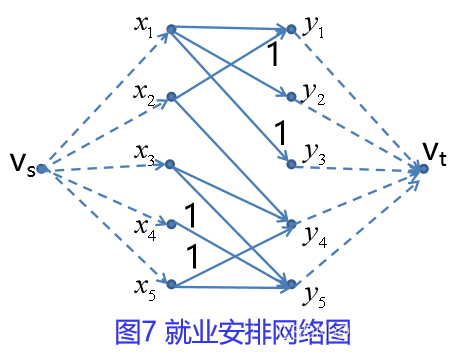
数学建模——最大流问题(配合例子说明)
目录 一、最大流有关的概念 例1 1、容量网络的定义 2、符号设置 3、建立模型 3.1 每条边的容量限制 3.2 平衡条件 3.3 网络的总流量 4、网络最大流数学模型 5、计算 二、最小费用流 例2 【符号说明】 【建立模型】 (1)各条边的流量限制 &a…...

AAOS CarMediaService 服务框架
文章目录 前言MediaSessionCarMediaService作用是什么?提供了哪些接口?如何使用?CarMediaService的实现总结 前言 CarMediaService 是AAOS中统一管理媒体播放控制、信息显示和用户交互等功能的服务。这一服务依赖于android MediaSession框架…...

gRPC之gRPC转换HTTP
1、gRPC转换HTTP 我们通常把RPC用作内部通信,而使用Restful Api进行外部通信。为了避免写两套应用,我们使用grpc- gateway 把gRPC转成HTTP。服务接收到HTTP请求后,grpc-gateway把它转成gRPC进行处理,然后以JSON 形式返回数据。…...

【十四】记一次MySQL宕机恢复过程,MySQL INNODB 损坏恢复
记一次MySQL宕机恢复过程 简介:一个业务数据库疏于运维管理,突然在今天崩溃宕机了,真是让人抓狂,上面也不知道积累了多久的数据,平时也没有定期做好备份,这下岂不是瞎了啊,经过不断的收集信息和…...
从0开始在Vscode中搭建Vue2/3项目详细步骤
1.安装node.js:Node.js下载安装及环境配置教程【超详细】_nodejs下载_WHF__的博客-CSDN博客 node.js自带npm,无需单独安装。 验证: node -v npm -v 2.先简单创建一个空文件夹,vscode进入该文件夹,并打开终端。 3.安装cnpm&…...

JavaScript ES6类的定义与继承
文章目录 一、class方式定义类1.认识class定义类2.类和构造函数的异同3.类的构造函数4.类的实例方法5.类的访问器方法6.类的静态方法 二、继承1.extends实现继承2.super关键字3.继承内置类4.类的混入mixin 三、ES6转ES51.class转换2.extends转换 四、多态 一、class方式定义类 …...

中科芯与IAR共建生态合作,IAR集成开发环境全面支持CKS32系列MCU
中国上海–2023年10月18日–嵌入式开发软件和服务的全球领导者IAR今日宣布,与中科芯集成电路有限公司(以下简称中科芯)达成生态合作,IAR已全面支持CKS32系列MCU的应用开发。这一合作将进一步推动嵌入式系统的发展,并为…...
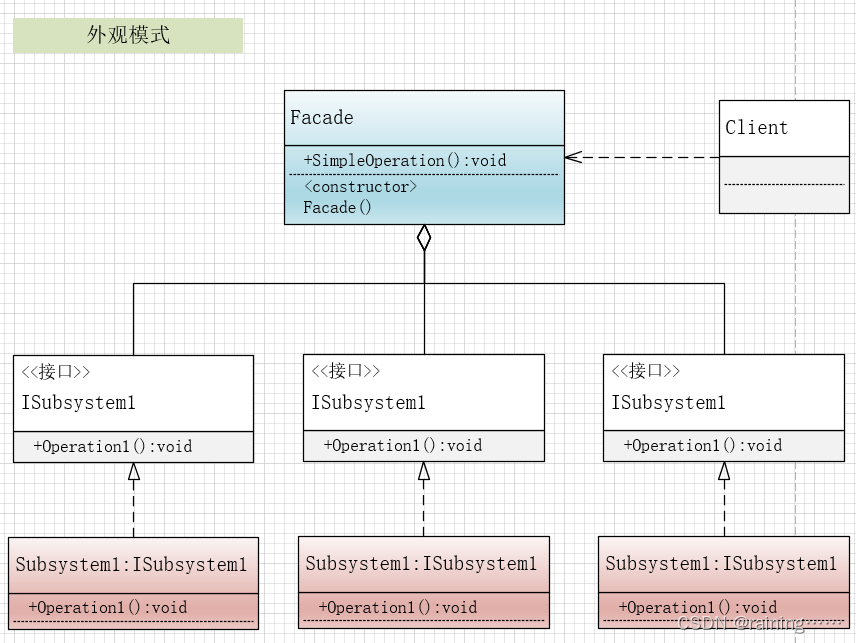
设计模式:外观模式(C#、JAVA、JavaScript、C++、Python、Go、PHP)
大家好!本节主要介绍设计模式中的外观模式。 简介: 外观模式,它是一种设计模式,它为子系统中的一组接口提供一个统一的、简单的接口。这种模式主张按照描述和判断资料来评价课程,关键活动是在课程实施的全过程中进行…...

Leetcode—34.在排序数组中查找元素的第一个和最后一个位置【中等】
2023每日刷题(六) Leetcode—34.在排序数组中查找元素的第一个和最后一个位置 实现代码 /*** Note: The returned array must be malloced, assume caller calls free().*/ int lower_bound(int *arr, int numsSize, int target) {// 左闭右开区间[lef…...
Java 8 新特性 Ⅱ
方法引用 举例: Integer :: compare 理解: 可以看作是基于lambda表达式的进一步简化 当需要提供一个函数式接口的实例时, 可以使用lambda表达式提供实例 当满足一定条件下, 可以使用方法引用or构造器引用替换lambda表达式 实质: 方法引用作为函数式接口的实例 (注: 需要熟悉…...

C语言学习书籍推荐
C语言学习书籍推荐如下: 《C程序设计语言》(The C Programming language):这本书由C语言创始人Brian W. Kernighan和Dennis M. Ritchie所写,是介绍标准C语言及其程序设计方法的权威性经典著作。《C陷阱与缺陷》&#…...
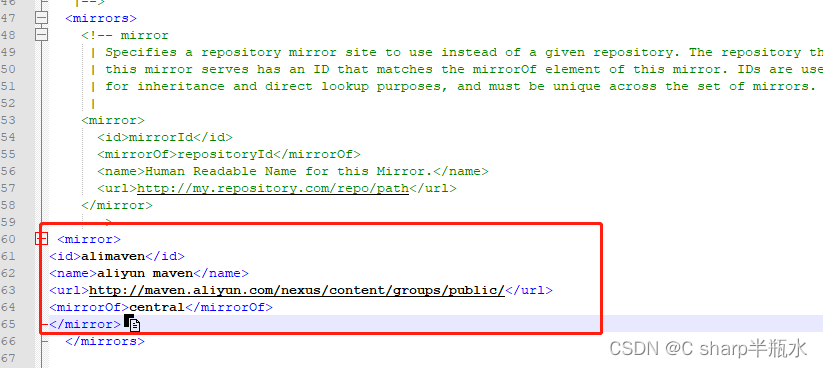
IntelliJ IDEA Maven加载超时问题
IDEA创建Maven项目遇到如下错误: Could not transfer artifact org.apache.maven.plugins:maven-compiler-plugin:pom:3.10.1 from/to central (Central Repository:): Connect to repo.maven.apache.org:443 [repo.maven.apache.org/146.75.112.215] failed: conn…...

Spring中事务失效的几种场景及解决办法
未抛出异常:如果在一个带有事务的方法中没有抛出异常,Spring无法检测到事务失败,从而无法回滚。解决方法是确保在事务中遇到错误时抛出异常。 异常被捕获:如果在一个带有事务的方法中抛出异常,但被捕获并处理了&#…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
