数学建模——最大流问题(配合例子说明)
目录
一、最大流有关的概念
例1
1、容量网络的定义
2、符号设置
3、建立模型
3.1 每条边的容量限制
3.2 平衡条件
3.3 网络的总流量
4、网络最大流数学模型
5、计算
二、最小费用流
例2
【符号说明】
【建立模型】
(1)各条边的流量限制
(2)网络总流量
(3)网络总费用
(4)中间点的流量平衡
【数学模型】
【模型求解】
三、最大匹配问题
例3
【问题假设】
【问题分析】
【符号设置】
【数学模型】
【模型求解】
一、最大流有关的概念
最大流是应用广泛的一类问题,例如交通运输网络中的人流、车流、物流;供水网络中的水流、金融系统中的资金流;通讯系统中的信息流。上世纪50年代Ford,Fulkerson建立的《网络流理论》是网络应用的基础。
例1
如图1所示网络为输油管道网络,vs为起点,vt为终点,v1,v2,v3,v4为中转站,边上的数字表示该管道的最大输油能力(t/h)。问如何安排各管道的输油量,才能使得从vs到vt的输油量最大。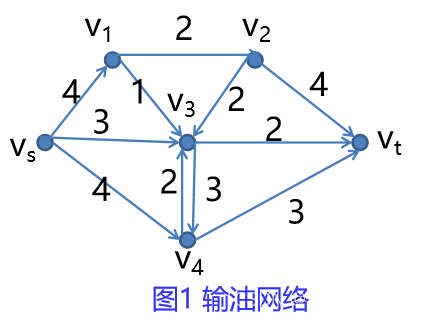
1、容量网络的定义
设有连通图G=(V,E),G的每一条边(vi,vj)上有非负数cij称为容量,仅有一个入次为0的点vs称为发点(源),一个出次为0的点vt称为收点(汇),其余点位中间点,这样的网络G称为容量网络,记为G=(V,E,C)。如图1所示。
2、符号设置
- Cij 边(i,j)的容量限制;
- fij 边(i,j)的实际流量;(称f={fij}为网络的一个流。)
- W 网络的总流量;
3、建立模型
3.1 每条边的容量限制
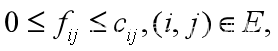
3.2 平衡条件
对中间点u,流入=流出,即
3.3 网络的总流量
称发点流量之和或汇点流量之和为网络总流量(忽略损失)。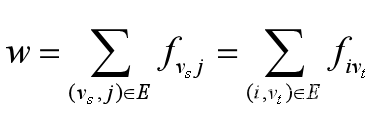
4、网络最大流数学模型
![]()
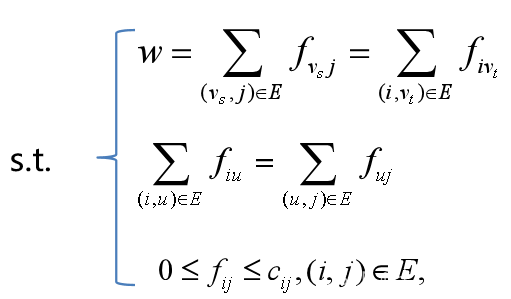
5、计算
编写例1的Lingo计算程序,将计算结果填入表1,将数据反映如图1,得到图2.
sets:
dian/vs v1 v2 v3 v4 vt/:;
bian(dian,dian)/vs,v1 vs,v3 vs,v4 v1,v2 v1,v3 v2,v3 v2,vt v3,vt v3,v4 v4,v3 v4,vt/:c,f;
endsets
data:
c=4 3 4 2 1 2 4 2 3 2 3;
enddata
max=w;
w=@sum(bian(i,j)|j#eq#6:f(i,j));
@for(bian(i,j):f(i,j)<c(i,j));
@for(dian(k)|k#ne#1#and#k#ne#6:@sum(bian(i,k):f(i,k))=@sum(bian(k,j):f(k,j)));表1 流量分布(不唯一)
| fij | V1 | V2 | V3 | v4 | vt |
| Vs | 3 | 4 | |||
| V1 | 2 | 1 | |||
| V2 | 2 | ||||
| V3 | 1 | 2 | |||
| v4 | 2 | 3 |
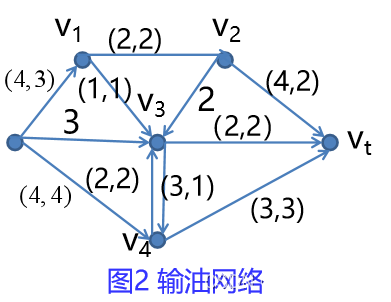
如图2所示,称形如(vs,v4),(v4,vt),(v4,v3),(v1,v2),(v1,v3)为饱和边;其余的边都是非饱和边。
要增大网络的流量,必须对饱和边扩容!!
二、最小费用流
设G=(V,E,C)为流量网络,边(i,j)除了容量限制cij外,还有因为流量而产生的单位费用dij(dij>0),记为G=(V,E,C,d)。这时如果不管流量大小,而只把网络流产生的费用当产目标,最优解必定是0,即各条边的实际流量为0时费用最小。研究方法必须改变为保持流量一定的情况下,使得流量产生的总费用最小。当网络流量保持最大而流量费用最小的网络流称为最小费用最大流。
例2
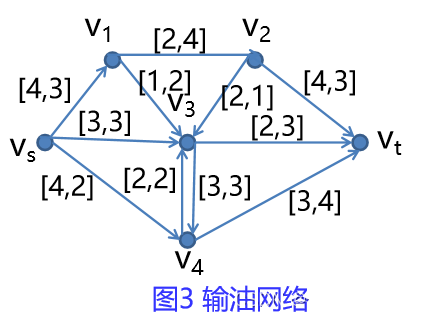
如图3所示网络G=(V,E,c,d),每条边有两个数字,第一个是容量限制,第二个是流量产生的单位费用。求该网络的最小费用最大流(最大流例1求得为7)。
【符号说明】
- G=(V,E,c,d] 如图3所示网络图;
- Cij 边(i,j)的管道容量限制;
- Dij 边(i,j)的单位费用;
- Xij 边(i,j)的实际流量;
- W 网络G的总流量。
【建立模型】
(1)各条边的流量限制
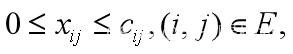
(2)网络总流量
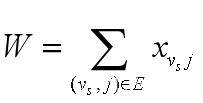
(3)网络总费用
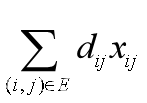
(4)中间点的流量平衡

【数学模型】
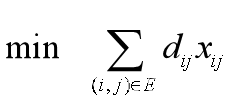
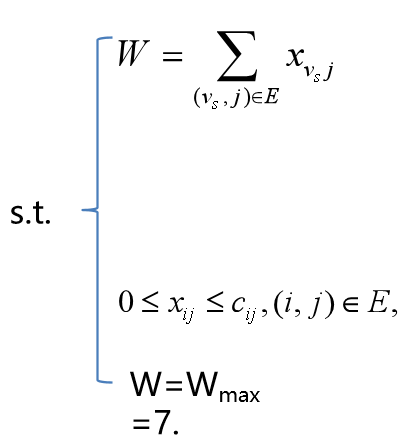
【模型求解】
编写lingo求解程序,计算得个各条边的实际流量见表2和总费用为50.(总流量为7时)
sets:
dian/vs v1 v2 v3 v4 vt/:;
bian(dian,dian)/vs,v1 vs,v3 vs,v4 v1,v2 v1,v3 v2,v3 v2,vt v3,vt v3,v4 v4,v3 v4,vt/:c,x,d;
endsets
data:
c=4 3 4 2 1 2 4 2 3 2 3;
d=3 3 2 4 2 1 3 3 3 2 4;
enddata
min=@sum(bian:d*x);
w=@sum(bian(i,j)|j#eq#6:x(i,j));
@for(bian(i,j):x(i,j)<c(i,j));
@for(dian(k)|k#ne#1#and#k#ne#6:@sum(bian(i,k):x(i,k))=@sum(bian(k,j):x(k,j)));
w=7;
表2 最小费用的流量分布
| fij | V1 | V2 | V3 | v4 | vt |
| Vs | 2 | 2 | 3 | ||
| V1 | 2 | ||||
| V2 | 2 | ||||
| V3 | 2 | ||||
| v4 | 3 |
三、最大匹配问题
问题来源:
有n个人,m件工作,每个人的工作能力不同,各能胜任某几项工作。假设每个只做一件工作;一件工作只需一个人做,怎样分配才能使得尽量多的工人有工作。
转化为匹配问题:
- x1,x2,…,xn表示工人;
- y1,y2,…,ym表示工作,
- X表示{x1,x2,…,xn}, Y表示{y1,y2,…,ym}。
这样就产生一个二部图G=(X,Y,E),其中E中的边(xi,yj)就表示xi胜任工作yj。如图4所示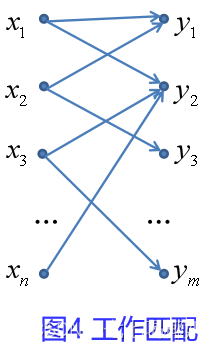
匹配定义:
二部图G=(X,Y,E),M是E的子集,M中任意两条边都没有公共端点,则称M是G的一个匹配(对集)。使得|M|达到最大的匹配称为最大匹配。
例3
设有5位待业者,5项工作,他们各自能胜任的工作情况如图5所示,设计一个就业方案,使尽量多人能就业。
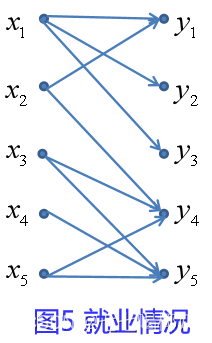
【问题假设】
一人最多一工作,一工作最多一人。
【问题分析】
注意到,对xi来说,出次可能不唯一,但最多有一条边可能实现;对yj来说,入次可能不唯一,但也最多一条边实现。根据流量平衡,在xi前置vs作为发点;在yj后置vt作为汇点,将图5改造为流量网络,见图六。
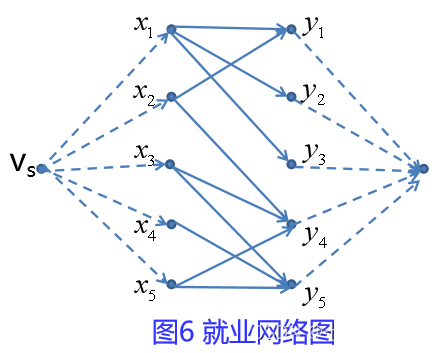
如图6所示流量网络图G=(V,E,C),其中每条边的容量都为1.
【符号设置】
- G=(V,E,C)流量网络图,如图6;
- vs 发点;
- vt 汇点;
- x1,…,x5,y1,…,y5,网络中间点;
- Cij 边(i,j)的容量限制,且cij=1,(i,j)∈E;
- xij 边(i,j)的实际流量,且只取0-1;
【数学模型】
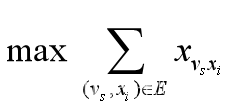
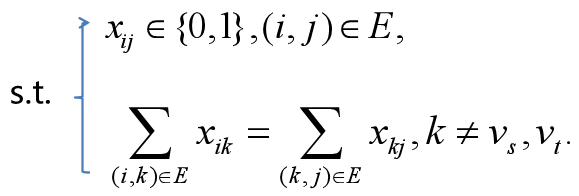
【模型求解】
编写Lingo程序,计算得到最大匹配为4,具体安排反映在图6上,见图7.
sets:
dian/vs x1 x2 x3 x4 x5 y1 y2 y3 y4 y5 vt/:;
bian(dian,dian)/vs,x1 vs,x2 vs,x3 vs,x4 vs,x5
x1,y1 x1,y2 x1,y3 x2,y1 x2,y4 x3,y4 x3,y5 x4,y5
x5,y4 x5,y5 y1,vt y2,vt y3,vt y4,vt y5,vt/:x,c;
endsets
data:
c=1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1;
enddata
n=@size(dian);
max=@sum(bian(i,j)|i#eq#1:x(i,j));
@for(bian:@bin(x));
@for(bian:x<c);
@for(dian(k)|k#ne#1#and#k#ne#n:@sum(bian(i,k):x(i,k))=@sum(bian(k,j):x(k,j))); 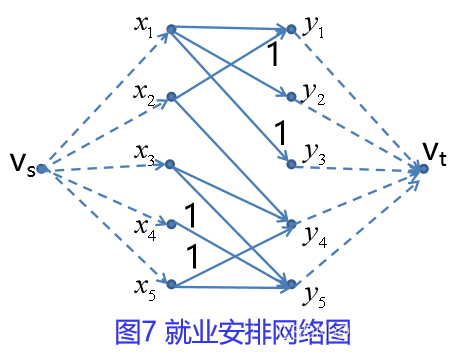
相关文章:

数学建模——最大流问题(配合例子说明)
目录 一、最大流有关的概念 例1 1、容量网络的定义 2、符号设置 3、建立模型 3.1 每条边的容量限制 3.2 平衡条件 3.3 网络的总流量 4、网络最大流数学模型 5、计算 二、最小费用流 例2 【符号说明】 【建立模型】 (1)各条边的流量限制 &a…...

AAOS CarMediaService 服务框架
文章目录 前言MediaSessionCarMediaService作用是什么?提供了哪些接口?如何使用?CarMediaService的实现总结 前言 CarMediaService 是AAOS中统一管理媒体播放控制、信息显示和用户交互等功能的服务。这一服务依赖于android MediaSession框架…...

gRPC之gRPC转换HTTP
1、gRPC转换HTTP 我们通常把RPC用作内部通信,而使用Restful Api进行外部通信。为了避免写两套应用,我们使用grpc- gateway 把gRPC转成HTTP。服务接收到HTTP请求后,grpc-gateway把它转成gRPC进行处理,然后以JSON 形式返回数据。…...

【十四】记一次MySQL宕机恢复过程,MySQL INNODB 损坏恢复
记一次MySQL宕机恢复过程 简介:一个业务数据库疏于运维管理,突然在今天崩溃宕机了,真是让人抓狂,上面也不知道积累了多久的数据,平时也没有定期做好备份,这下岂不是瞎了啊,经过不断的收集信息和…...
从0开始在Vscode中搭建Vue2/3项目详细步骤
1.安装node.js:Node.js下载安装及环境配置教程【超详细】_nodejs下载_WHF__的博客-CSDN博客 node.js自带npm,无需单独安装。 验证: node -v npm -v 2.先简单创建一个空文件夹,vscode进入该文件夹,并打开终端。 3.安装cnpm&…...

JavaScript ES6类的定义与继承
文章目录 一、class方式定义类1.认识class定义类2.类和构造函数的异同3.类的构造函数4.类的实例方法5.类的访问器方法6.类的静态方法 二、继承1.extends实现继承2.super关键字3.继承内置类4.类的混入mixin 三、ES6转ES51.class转换2.extends转换 四、多态 一、class方式定义类 …...

中科芯与IAR共建生态合作,IAR集成开发环境全面支持CKS32系列MCU
中国上海–2023年10月18日–嵌入式开发软件和服务的全球领导者IAR今日宣布,与中科芯集成电路有限公司(以下简称中科芯)达成生态合作,IAR已全面支持CKS32系列MCU的应用开发。这一合作将进一步推动嵌入式系统的发展,并为…...
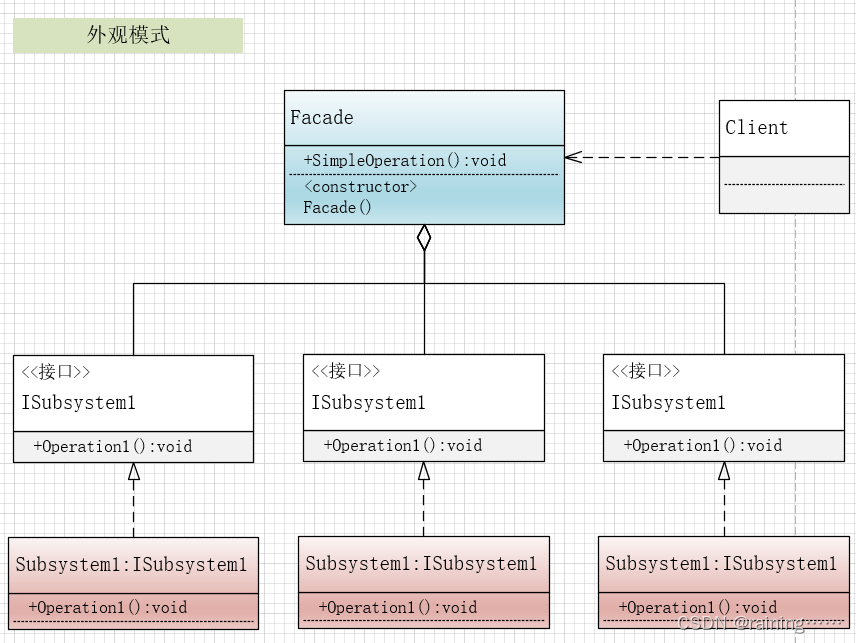
设计模式:外观模式(C#、JAVA、JavaScript、C++、Python、Go、PHP)
大家好!本节主要介绍设计模式中的外观模式。 简介: 外观模式,它是一种设计模式,它为子系统中的一组接口提供一个统一的、简单的接口。这种模式主张按照描述和判断资料来评价课程,关键活动是在课程实施的全过程中进行…...

Leetcode—34.在排序数组中查找元素的第一个和最后一个位置【中等】
2023每日刷题(六) Leetcode—34.在排序数组中查找元素的第一个和最后一个位置 实现代码 /*** Note: The returned array must be malloced, assume caller calls free().*/ int lower_bound(int *arr, int numsSize, int target) {// 左闭右开区间[lef…...
Java 8 新特性 Ⅱ
方法引用 举例: Integer :: compare 理解: 可以看作是基于lambda表达式的进一步简化 当需要提供一个函数式接口的实例时, 可以使用lambda表达式提供实例 当满足一定条件下, 可以使用方法引用or构造器引用替换lambda表达式 实质: 方法引用作为函数式接口的实例 (注: 需要熟悉…...

C语言学习书籍推荐
C语言学习书籍推荐如下: 《C程序设计语言》(The C Programming language):这本书由C语言创始人Brian W. Kernighan和Dennis M. Ritchie所写,是介绍标准C语言及其程序设计方法的权威性经典著作。《C陷阱与缺陷》&#…...
IntelliJ IDEA Maven加载超时问题
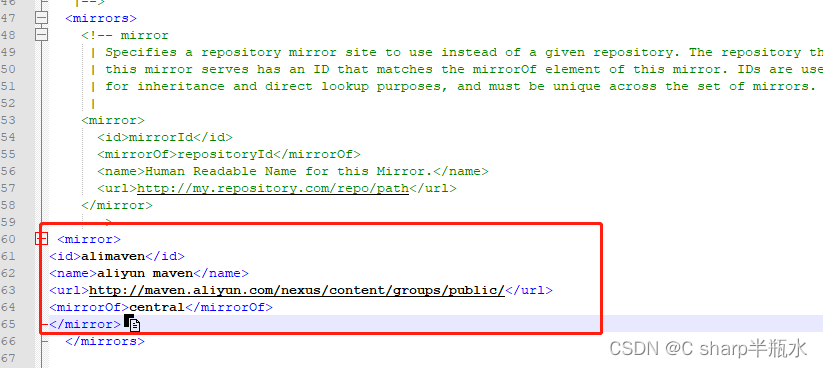
IDEA创建Maven项目遇到如下错误: Could not transfer artifact org.apache.maven.plugins:maven-compiler-plugin:pom:3.10.1 from/to central (Central Repository:): Connect to repo.maven.apache.org:443 [repo.maven.apache.org/146.75.112.215] failed: conn…...

Spring中事务失效的几种场景及解决办法
未抛出异常:如果在一个带有事务的方法中没有抛出异常,Spring无法检测到事务失败,从而无法回滚。解决方法是确保在事务中遇到错误时抛出异常。 异常被捕获:如果在一个带有事务的方法中抛出异常,但被捕获并处理了&#…...
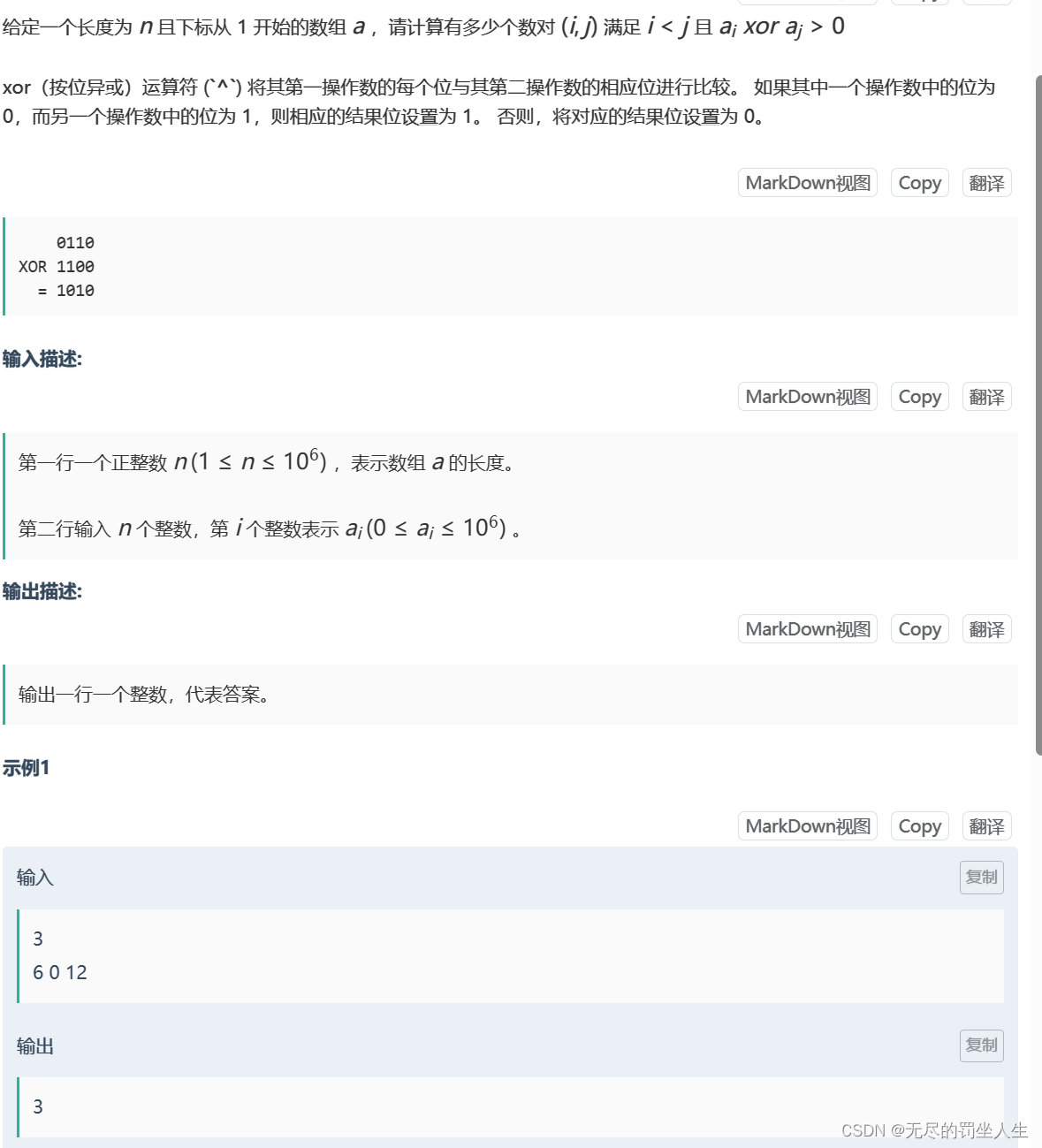
第五届太原理工大学程序设计竞赛新生赛(初赛)题解
第五届太原理工大学程序设计竞赛新生赛(初赛)题解 时隔半年重做一次,还是有几道不会,,,,, ⭐️A.饿饿饭饭 题目: 🌟题解: 很简单,签…...
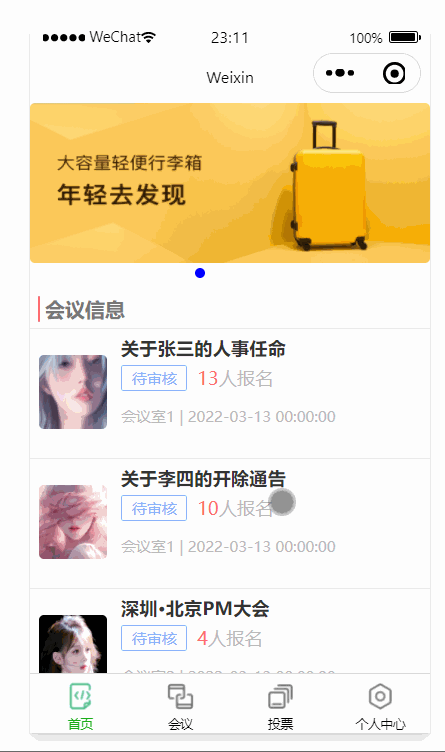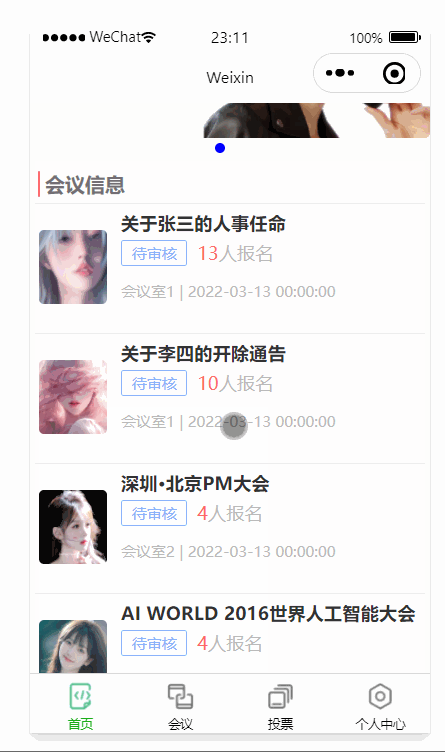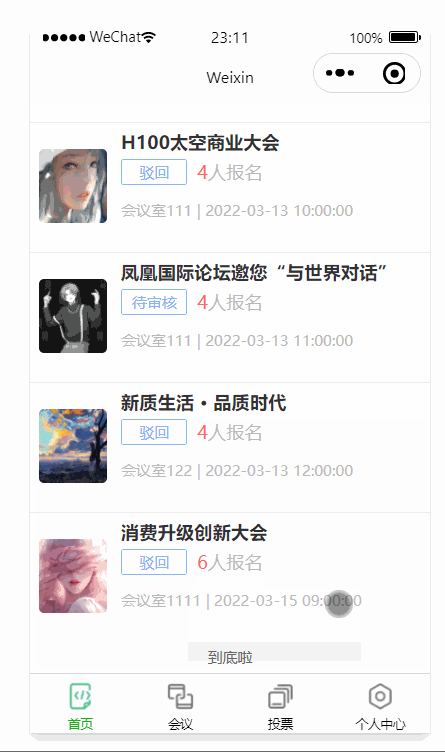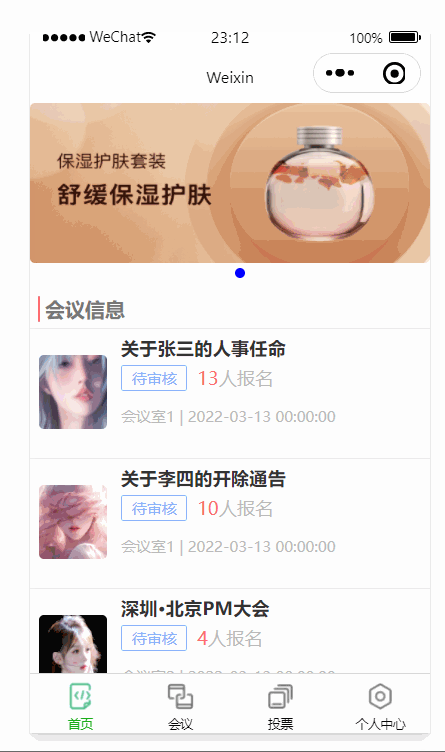
微信小程序开发之后台数据交互及wxs应用
目录 一、后端准备 1. 应用配置 2. 数据源配置 二、数据库 1. 创建 2. 数据表 3. 数据测试 三、前端 1. 请求方法整合 2. 数据请求 3. WXS的使用 4. 样式美化 5. 页面 一、后端准备 通过SpringMVC及mybatis的技术学习,还有前后端分离的技术应用&…...

Java进阶篇--并发容器之ThreadLocal内存泄漏
目录 ThreadLocal内存泄漏的原因? 改进和优化 cleanSomeSlots方法 expungeStaleEntry方法 replaceStaleEntry方法 为什么使用弱引用? Thread.exit() ThreadLocal内存泄漏最佳解决方案 在使用完毕后立即清理ThreadLocal 使用InheritableThreadL…...

js实现红包雨功能(canvas,react,ts),包括图片不规则旋转、大小、转速、掉落速度控制、屏幕最大红包数量控制等功能
介绍 本文功能由canvas实现红包雨功能(index.tsx)本文为react的ts版。如有其他版本需求可评论区观赏地址,需过墙 import React, { Component } from react; // import ./index.css; import moneyx from /assets/images/RedEnvelopeRain/bal…...
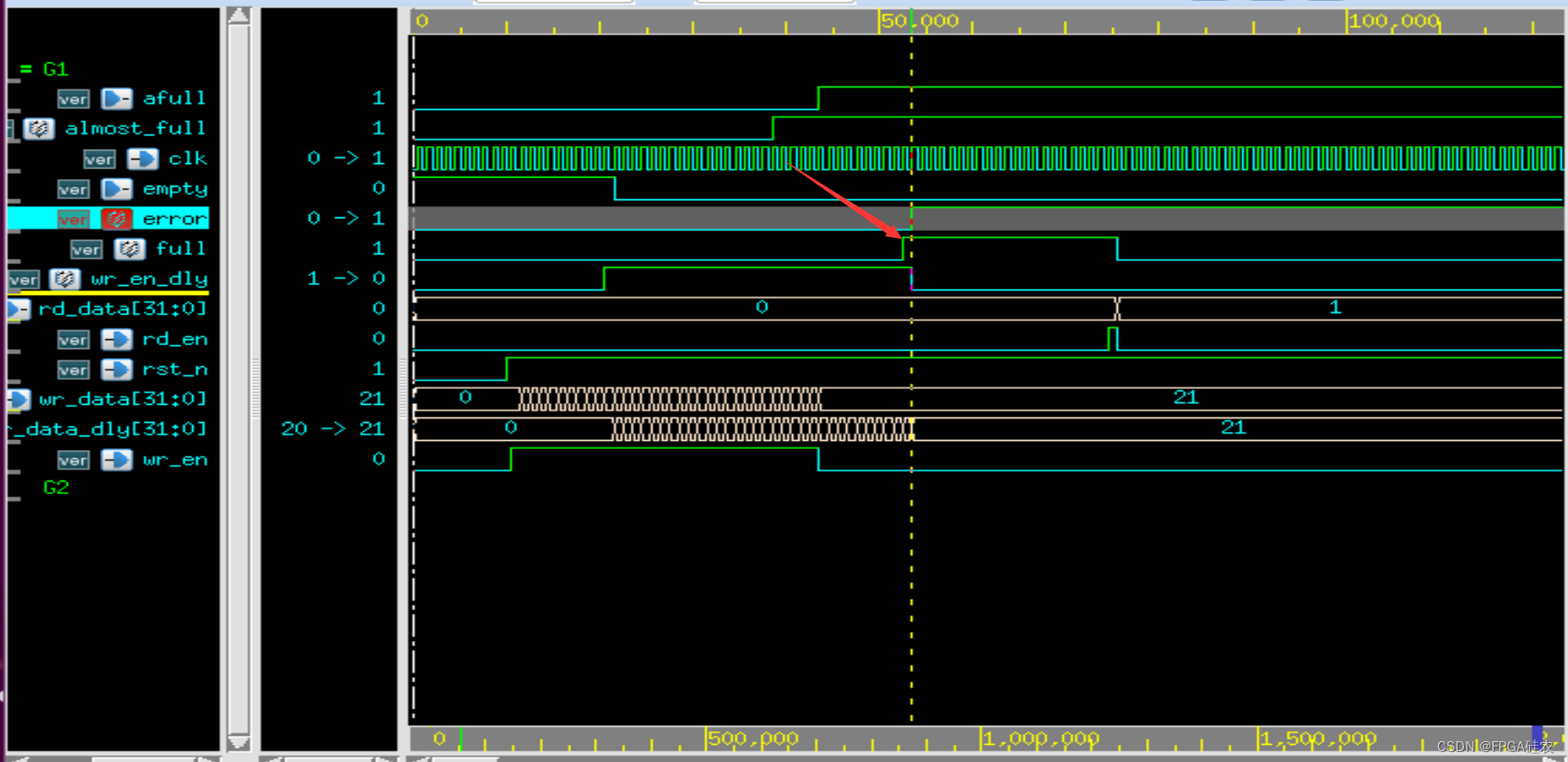
【数字IC设计/FPGA】FIFO与流控机制
流控,简单来说就是控制数据流停止发送。常见的流控机制分为带内流控和带外流控。 FIFO的流水反压机制 一般来说,每一个fifo都有一个将满阈值afull_value(almost full)。当fifo内的数据量达到或超过afull_value时,将满…...
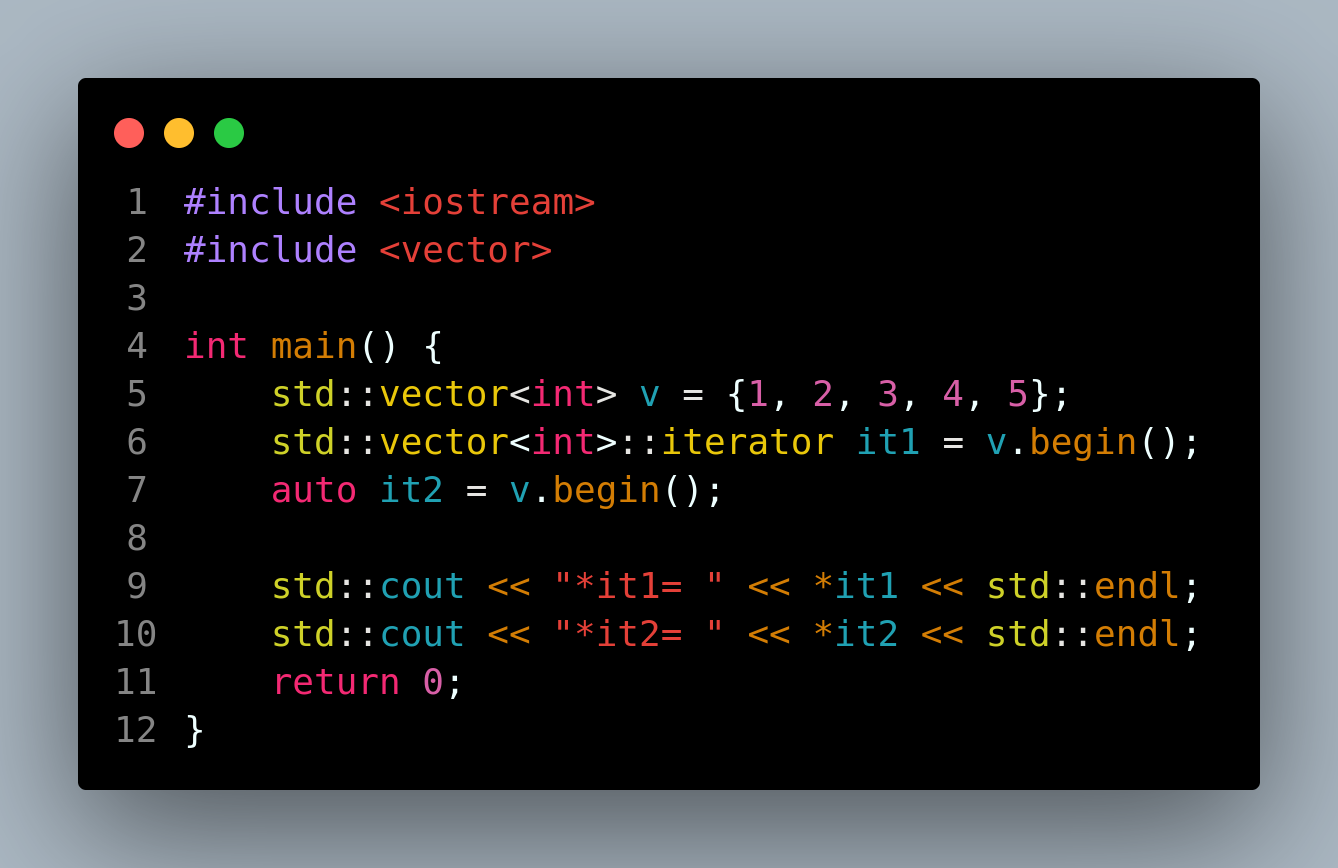
C++笔记之遍历vector的所有方式
C笔记之遍历vector的所有方式 —— 2023年4月15日 上海 code review 文章目录 C笔记之遍历vector的所有方式1.普通for循环2.迭代器版3.const迭代器4.C11引入的范围for循环5.使用auto关键字和迭代器6.使用std::for_each算法7.使用std::for_each和lambda表达式8.普通版vector::at…...

OpenCV 笔记(2):图像的属性以及像素相关的操作
Part11. 图像的属性 11.1 Mat 的主要属性 在前文中,我们大致了解了 Mat 的基本结构以及它的创建与赋值。接下来我们通过一个例子,来看看 Mat 所包含的常用属性。 先创建一个 3*4 的四通道的矩阵,并打印出其相关的属性,稍后会详细…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

初探用uniapp写微信小程序遇到的问题及解决(vue3+ts)
零、关于开发思路 (一)拿到工作任务,先理清楚需求 1.逻辑部分 不放过原型里说的每一句话,有疑惑的部分该问产品/测试/之前的开发就问 2.页面部分(含国际化) 整体看过需要开发页面的原型后,分类一下哪些组件/样式可以复用,直接提取出来使用 (时间充分的前提下,不…...

MAZANOKE结合内网穿透技术实现跨地域图像优化服务的远程访问过程
文章目录 前言1. 关于MAZANOKE2. Docker部署3. 简单使用MAZANOKE4. 安装cpolar内网穿透5. 配置公网地址6. 配置固定公网地址总结 前言 在数字世界高速发展的今天,您是否察觉到那些静默增长的视觉数据正在悄然蚕食存储空间?随着影像记录成为日常习惯&…...

Vue 3 Teleport 实战:优雅实现模态框、通知和全局组件
Vue 3 Teleport:突破 DOM 层级限制的组件渲染利器 在 Vue 应用开发中,组件通常与其模板的 DOM 结构紧密耦合。但当处理模态框(Modal)、通知(Toast)或全局 Loading 指示器时,这种耦合会成为障碍…...
