在pytorch中对于张量维度的理解
原文参考链接:
https://blog.csdn.net/qq_36930921/article/details/121670945.
https://zhuanlan.zhihu.com/p/356951418
张量的计算:https://zhuanlan.zhihu.com/p/140260245
学习过程中对知识的补充学习,谨防原文失效,请大家支持原创
神经网络的数据显示:
- 使用的数据存储在多维Numpy数组中,也叫张量(tensor)。一般来说,当前所有机器学习系统都使用张量作为基本数据结构。张量对这个领域非常重要,重要到Google的TensorFlow都以他来命名。那么什么是张量?
- 张量这一概念的核心在于,它是一个数据容器。它包含的数据几乎总是数值数据,因此它是数字的容器。你可能对矩阵很熟悉,它是二维张量。张量是矩阵向任意维度的推广注意,张量的维度(dimension)通常叫作轴(axis)]。
1.1标量(0D张量)
仅包含一个数字的张量叫作标量(scalar,也叫标量张量、零维张量、0D 张量)。在 Numpy中,一个 float32 或 float64 的数字就是一个标量张量(或标量数组)。你可以用 ndim 属性来查看一个 Numpy 张量的轴的个数。标量张量有 0 个轴( ndim == 0 )。张量轴的个数也叫作阶(rank)。下面是一个 Numpy 标量。
import numpy as np
x = np.array(12)
print(x.ndim)
x
>>>运行结果:
>>>0
>>>array(12)
1.2 向量(1D 张量)
数字组成的数组叫作向量(vector)或一维张量(1D 张量)。一维张量只有一个轴。下面是一个 Numpy 向量。
import numpy as np
x = np.array([12, 3, 6, 14, 7])
print(x.ndim)
x
>>>运行结果:
>>>1
>>>array([12,3,6,14,7])
这个向量有 5 个元素,所以被称为 5D 向量。不要把 5D 向量和 5D 张量弄混! 5D 向量只有一个轴,沿着轴有 5 个维度,而 5D 张量有 5 个轴(沿着每个轴可能有任意个维度)。维度(dimensionality)可以表示沿着某个轴上的元素个数(比如 5D 向量),也可以表示张量中轴的个数(比如 5D 张量),这有时会令人感到混乱。对于后一种情况,技术上更准确的说法是 5 阶张量(张量的阶数即轴的个数),但 5D 张量这种模糊的写法更常见。
1.3矩阵(2D张量)
① 向量组成的数组叫作矩阵(matrix)或二维张量(2D 张量)。矩阵有 2 个轴(通常叫作行和列)。你可以将矩阵直观地理解为数字组成的矩形网格。下面是一个 Numpy 矩阵。
import numpy as np
x = np.array([[5, 78, 2, 34, 0],[6, 79, 3, 35, 1],[7, 80, 4, 36, 2]])
print(x.ndim)
>>>数据结果
>>>2
1.4 3D 张量与更高维张量
将多个矩阵组合成一个新的数组,可以得到一个 3D 张量,你可以将其直观地理解为数字组成的立方体。下面是一个 Numpy 的 3D 张量。
import numpy as np
x = np.array([[[5, 78, 2, 34, 0],[6, 79, 3, 35, 1],[7, 80, 4, 36, 2]],[[5, 78, 2, 34, 0],[6, 79, 3, 35, 1],[7, 80, 4, 36, 2]],[[5, 78, 2, 34, 0],[6, 79, 3, 35, 1],[7, 80, 4, 36, 2]]])
print(x.ndim)>>>数据结果
>>>3
将多个 3D 张量组合成一个数组,可以创建一个 4D 张量,以此类推。深度学习处理的一般是 0D 到 4D 的张量,但处理视频数据时可能会遇到 5D 张量。
1.5关键属性
张量是由以下三个关键属性来定义的。
- 轴的个数(阶)。例如,3D 张量有 3 个轴,矩阵有 2 个轴。这在 Numpy 等 Python 库中也叫张量的 ndim 。
- 形状。这是一个整数元组,表示张量沿每个轴的维度大小(元素个数)。例如,前面矩阵示例的形状为 (3, 5) ,3D 张量示例的形状为
(3, 3, 5) 。向量的形状只包含一个元素,比如 (5,) ,而标量的形状为空,即 () 。 - 数据类型(在 Python 库中通常叫作 dtype )。这是张量中所包含数据的类型,例如,张量的类型可以是 float32 、 uint8 、 float64 等。在极少数情况下,你可能会遇到字符( char )张量。注意,Numpy(以及大多数其他库)中不存在字符串张量,因为张量存储在预先分配的连续内存段中,而字符串的长度是可变的,无法用这种方式存储。
1.6现实世界中的数据张量
我们用几个你未来会遇到的示例来具体介绍数据张量。你需要处理的数据几乎总是以下类别之一。
- 向量数据:2D 张量,形状为 (samples, features) 。
- 时间序列数据或序列数据:3D 张量,形状为 (samples, timesteps, features) 。
- 图像:4D张量,形状为 (samples, height, width, channels) 或 (samples,
channels,height, width) 。 - 视频:5D张量,形状为 (samples, frames, height, width, channels) 或
(samples,frames, channels, height, width) 。
1.7如何判断张量的batch数、行、列、深度
从左边开始数连续[的数量,最多有X个[说明是X维张量。上面的例子就是4维张量。
shape属性中的元素大于等于3时,可以用3维空间来理解。
shape=(3, 4, 2)时,表示3个4行2列的张量
shape=(2, 3, 4, 2)时,表示有2个 3行4列深度为2的张量
shape=(6, 2, 3, 4, 2)时,表示有6个四维张量,这个四维张量又可以表示为2个 3行4列深度为2的张量。
——————————————————————————————
例如:
张量的阶数有时也称维度,或者轴axis。比如矩阵[[1,2],[3,4]],是一个二维张量。
- 沿着第0个轴(axis=0)可以看到[1,2],[3,4]两个向量
- 沿着第1个轴(axis=1)可以看到[1,3],[2,4]两个向量。

一维向量:
const1 = tf.constant([1,2,3,4],tf.float16)二维张量:
# 三行四列
const2 = tf.constant([[1,2,3,4],[5,6,7,8],[9,10,11,12]
],tf.float16)几何表示:

三维张量:
# 3行4列深度为2
const3 = tf.constant([[[1,2],[3,4],[5,6],[7,8]],[[11, 12], [13, 14], [15, 16], [17, 18]],[[21, 22], [23, 24], [25, 26], [27, 28]]
],tf.float16)
shape = (3,4,2)几何表示:

四维张量 (仅用于理解,坐标系已经不再适用)
# 3行4列深度为2
const3 = tf.constant([#第一个3行4列深度为2的三维张量[[[1,2],[3,4],[5,6],[7,8]],[[11, 12], [13, 14], [15, 16], [17, 18]],[[21, 22], [23, 24], [25, 26], [27, 28]]],#第二个3行4列深度为2的三维张量[[[1,2],[3,4],[5,6],[7,8]],[[11, 12], [13, 14], [15, 16], [17, 18]],[[21, 22], [23, 24], [25, 26], [27, 28]]]
],tf.float16)
shape = (2,3,4,2)几何表示:

————————————————————————————
图像数据
① 图像通常具有三个维度:高度、宽度和颜色深度。虽然灰度图像(比如 MNIST 数字图像)只有一个颜色通道,因此可以保存在 2D 张量中,但按照惯例,图像张量始终都是 3D 张量,灰度图像的彩色通道只有一维。因此,如果图像大小为 256×256,那么 128 张灰度图像组成的批量可以保存在一个形状为 (128, 256, 256, 1) 的张量中,而 128 张彩色图像组成的批量则可以保存在一个形状为 (128, 256, 256, 3) 的张量中。
② 图像张量的形状有两种约定:通道在后(channels-last)的约定(在 TensorFlow 中使用)和通道在前(channels-first)的约定(在 Theano 中使用)。Google 的 TensorFlow 机器学习框架将颜色深度轴放在最后: (samples, height, width, color_depth) 。与此相反,Theano将图像深度轴放在批量轴之后: (samples, color_depth, height, width) 。如果采用 Theano 约定,前面的两个例子将变成 (128, 1, 256, 256) 和 (128, 3, 256, 256) 。Keras 框架同时支持这两种格式。
视频数据
① 视频数据是现实生活中需要用到 5D 张量的少数数据类型之一。视频可以看作一系列帧,每一帧都是一张彩色图像。由于每一帧都可以保存在一个形状为 (height, width, color_depth) 的 3D 张量中,因此一系列帧可以保存在一个形状为 (frames, height, width,color_depth) 的 4D 张量中,而不同视频组成的批量则可以保存在一个 5D 张量中,其形状为(samples, frames, height, width, color_depth) 。
② 举个例子,一个以每秒 4 帧采样的 60 秒 YouTube 视频片段,视频尺寸为 144×256,这个视频共有 240 帧。4 个这样的视频片段组成的批量将保存在形状为 (4, 240, 144, 256, 3)的张量中。总共有 106 168 320 个值!如果张量的数据类型( dtype )是 float32 ,每个值都是32 位,那么这个张量共有 405MB。好大!你在现实生活中遇到的视频要小得多,因为它们不以float32 格式存储,而且通常被大大压缩,比如 MPEG 格式。
时间序列数据或序列数据
① 当时间(或序列顺序)对于数据很重要时,应该将数据存储在带有时间轴的 3D 张量中。每个样本可以被编码为一个向量序列(即 2D 张量),因此一个数据批量就被编码为一个 3D 张量(见下图)

② 根据惯例,时间轴始终是第 2 个轴(索引为 1 的轴)。我们来看几个例子。
- 股票价格数据集。每一分钟,我们将股票的当前价格、前一分钟的最高价格和前一分钟的最低价格保存下来。因此每分钟被编码为一个 3D
向量,整个交易日被编码为一个形状为 (390, 3) 的 2D 张量(一个交易日有 390 分钟),而 250
天的数据则可以保存在一个形状为 (250, 390, 3) 的 3D 张量中。这里每个样本是一天的股票数据。 - 推文数据集。我们将每条推文编码为 280 个字符组成的序列,而每个字符又来自于128个字符组成的字母表。在这种情况下,每个字符可以被编码为大小为 128 的二进制向量(只有在该字符对应的索引位置取值为1,其他元素都为 0)。那么每条推文可以被编码为一个形状为 (280, 128) 的 2D 张量,而包含 100万条推文的数据集则可以存储在一个形状为 (1000000, 280, 128) 的张量中。
相关文章:

在pytorch中对于张量维度的理解
原文参考链接: https://blog.csdn.net/qq_36930921/article/details/121670945. https://zhuanlan.zhihu.com/p/356951418 张量的计算:https://zhuanlan.zhihu.com/p/140260245 学习过程中对知识的补充学习,谨防原文失效,请大家支…...
)
JAVA高级教程Java HashMap表达式(7)
目录 7、HashMap的使用students类 7、HashMap的使用 students类 package Map01;import java.util.Objects ;public class Students implements Comparable<Students>{private String name;private int stuNO;public Students() {}public Students(String age, int stuN…...

【iOS】JSON解析
JSON在Web开发和网络通信和传输中广泛应用,常用于存储和传输数据,这些数据一般也都是JSON格式,可以说绝大多数网络请求传输的数据都是JSON格式 在之前有关网络请求文章中,实现了网络数据加载流程,并对加载下来的JSON数…...
【java】A卷+B卷)
华为OD 最大差(100分)【java】A卷+B卷
华为OD统一考试A卷+B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应20022部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入: 我用夸克网盘分享了「华为O…...

打印新闻标题,使用封装get、set方法,打印前15个字符串
package day21; import java.util.ArrayList; import java.util.Collections;/*** author monian* Wo yi wu ta,wei shou shu er!*/ public class Homework01 {SuppressWarnings({"all"})public static void main(String[] args) {News news1 new News("新冠确…...

FL Studio21中文版本好用吗?值不值得下载
今天,我从一个FL Studio忠实且还算资深的用户角度,来为大家深度介绍并评测一下FL Studio的性能以及我四年的使用感受。 FL Studio是一款集剪辑、编曲、录音、混音一体的全能DAW(数字音频工作站)。其所有界面都是支持100%矢量化的…...

微信小程序进阶——Flex弹性布局轮播图会议OA项目(首页)
目录 一、Flex弹性布局 1.1 什么是Flex弹性布局 1.1.1 详解 1.1.2 图解 1.1.3 代码演示效果 1.2 Flex弹性布局的核心概念 1.3 Flex 弹性布局的常见属性 1.4 Flex弹性布局部分属性详解 1.4.1 flex-direction属性 1.4.2 flex-wrap属性 1.4.3 flex-flow属性 1.4.4 ju…...

工程监测仪器振弦传感器信号转换器在桥梁安全监测中的重要性
工程监测仪器振弦传感器信号转换器在桥梁安全监测中的重要性 桥梁是人类社会建设过程中最重要的交通基础设施之一,对于保障人民出行、促进经济发展具有极其重要的作用。由于桥梁结构在长期使用过程中受到环境因素和负荷的影响,会逐渐发生变形和损伤&…...

ArduPilot开源飞控之AP_OpticalFlow
ArduPilot开源飞控之AP_OpticalFlow 1. 源由2. 框架设计2.1 启动代码2.2 任务代码 update2.3 任务代码 handle_msg2.4 任务代码 handle_msp2.5 任务代码 do_aux_function 3. 重要例程3.1 AP_OpticalFlow3.2 init3.3 update3.4 handle_msg3.5 handle_msp3.6 start_calibration3.…...
RHCE8 资料整理(二)
RHCE8 资料整理 第二篇 用户及权限管理第8章 用户管理8.1 基本概念8.2 管理用户8.2.1 创建用户8.2.2 修改用户属性 8.3 用户的密码策略8.4 用户授权8.5 重置root密码 第9章 权限管理9.1 所有者和所属组9.2 查看及修改权限9.3 数字权限9.4 默认权限9.5 特殊权限9.6 隐藏权限 第1…...
— conftest.py文件)
pytest合集(11)— conftest.py文件
1、conftest.py文件 conftest.py文件是pytest框架中的一个特殊文件,用于定义共享的设置、夹具(fixture)和钩子函数(hook)。 在pytest中,conftest.py文件可以用于在整个测试项目中共享夹具、配置和钩子函数。通过在conftest.py文…...

completablefuture的使用
CompletableFuture使用详解 【Java异常】Variable used in lambda expression should be final or effectively final CompletableFuture原理与实践-外卖商家端API的异步化 项目描述 项目接口需要从下游多个接口获取数据,并且下游的网络不稳定还会涉及到循环调用…...
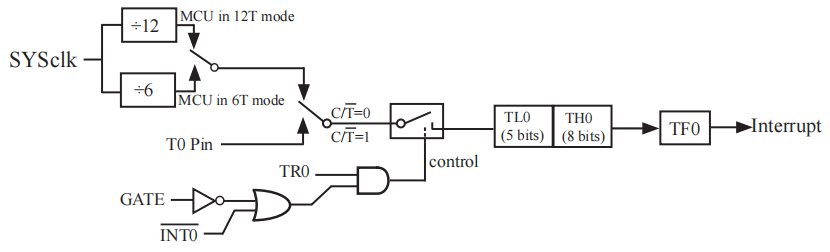
51单片机的时钟系统
1.简介 51内置的时钟系统可以用来计时,与主程序分割开来,在计时过程中不会终端主程序,还可以通过开启时钟中断来执行相应的操作。 2.单片机工作方式 单片机内部有两个十六位的定时器T0和T1。每个定时器有两种工作方式选择,分别…...

神经网络的问题总结
神经网络目前可以分为以下几类问题,每类问题都有其特点和不断取得的进展: 分类问题: 特点:在给定一组数据点的情况下,将它们分为不同的类别。进展:神经网络在图像分类、文本分类、音频分类等方面取得了显著…...

树莓派图像处理基础知识
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、基本函数1. cvtColor(src,tmp,COLOR_BGR2RGB);2.在OpenCV和Qt中,转换cv::Mat到QImage3.Canny(tmp,dst,30,255);4.dst matframe.clone();5.video…...

Kotlin中的Lambda表达式基本定义和使用
在Kotlin中,Lambda表达式是一种简洁的方式来定义匿名函数。Lambda表达式可以作为函数的实际参数或者返回值,使得函数成为高阶函数。本篇博客将介绍Lambda表达式的基本概念以及使用方法,并提供相关的示例代码。 Lambda表达式的基本概念 Lamb…...

递福巴士是不是骗局呢?
递福巴士的背景介绍 递福巴士是社区服务机构软件。递福巴士是一家提供公益服务的平台,为社区居民提供各种服务和支持的软件。多年来,递福巴士一直致力于社区服务和社会公益,积极推动社区的发展,改善社区居民的生活质量。 递福巴士…...
与torch.Size([0])的区别)
torch.Size([])与torch.Size([0])的区别
在PyTorch中,torch.Size([])和torch.Size([0])都表示一个空的维度(dimension)。然而,它们之间有微妙的区别。 torch.Size([]): 表示一个标量(scalar),即一个没有维度的张量。这个张量…...

DP基础相关笔记
基础 DP LIS LIS(Longest Increasing Subsequence),顾名思义,就是最长上升子序列问题。 在这里我们要区分一下子串和子序列的区别,很简单,子串连续,子序列可以不连续。然而就在几小时之前本蒟…...
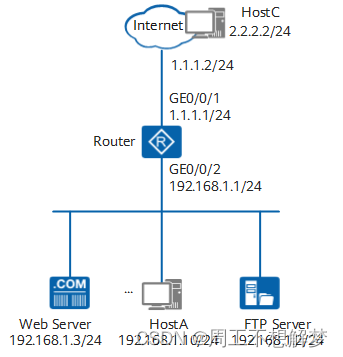
配置公网和私网用户通过非公网口的IP地址访问内部服务器和Internet示例
组网需求 如配置公网和私网用户通过非公网口的IP地址访问内部服务器和Internet示例所示,某小型企业内网部署了一台路由器、一台FTP服务器和一台Web服务器。路由器作为接入网关,为下挂的内网用户提供上网服务,主要包括浏览网页、使用即时通信…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
