探索未来的视觉革命:卷积神经网络的崭新时代(二)
💗💗💗欢迎来到我的博客,你将找到有关如何使用技术解决问题的文章,也会找到某个技术的学习路线。无论你是何种职业,我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章,也欢迎在文章下方留下你的评论和反馈。我期待着与你分享知识、互相学习和建立一个积极的社区。谢谢你的光临,让我们一起踏上这个知识之旅!
文章目录
- 🍋引言
- 🍋GoogleNet的架构
- 🍋1×1 convolution
- 🍋如何有效避免梯度消失?
- 🍋总结
本节在学完刘二大人的卷积神经网络进阶篇,令我感受颇深,下面我先说一下知识点,文章的结尾我再表达一下我的个人看法以及刘二大人对我们的建议。
🍋引言
本节介绍一下GoogleNet,首先说一下它的背景历史,GoogleNet是由Google研究员Christian Szegedy等人于2014年提出的深度卷积神经网络架构。它在当时的ImageNet图像分类挑战赛中取得了惊人的成绩,将错误率大幅度降低,标志着深度学习领域的一次巨大突破。
🍋GoogleNet的架构
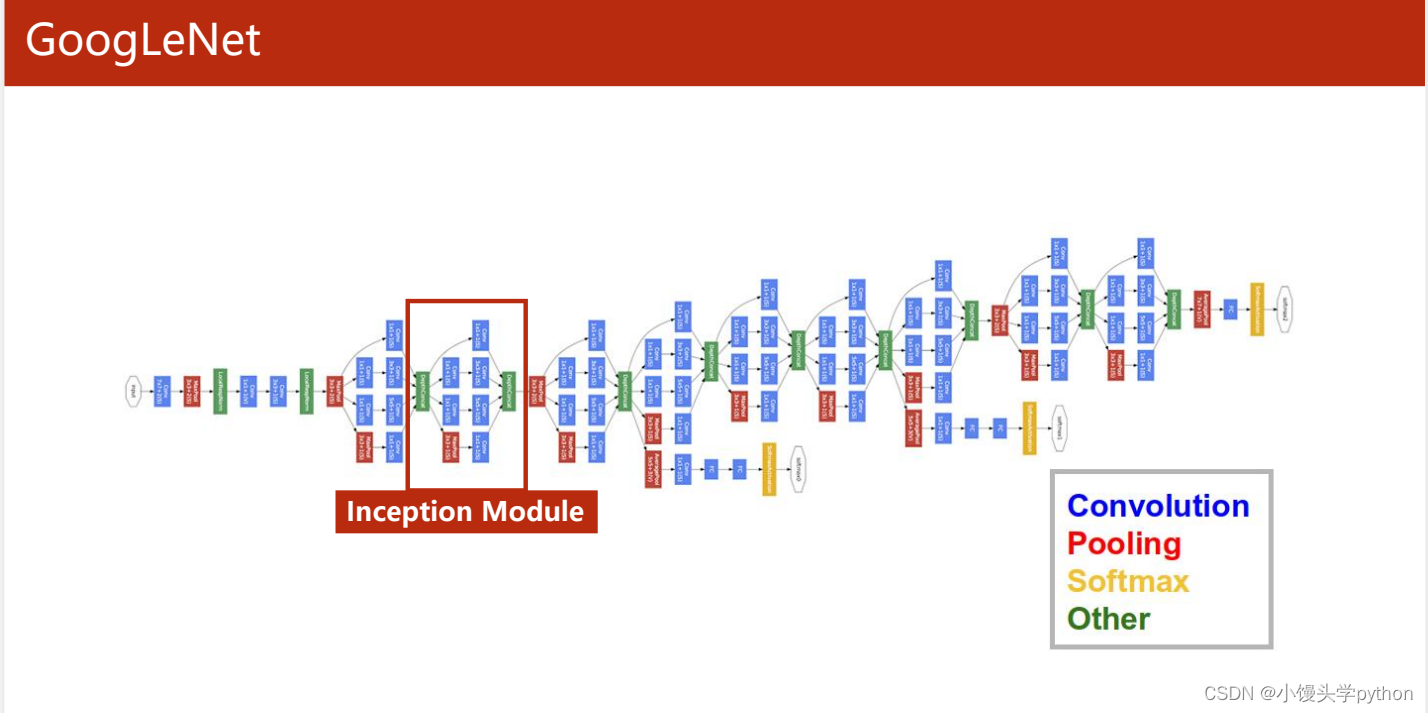
GoogleNet之所以引人注目,是因为它采用了一种全新的架构,即Inception架构。这个架构采用了多尺度卷积核,允许网络同时学习不同尺度的特征。这里解释一下就是类似于多条路一起跑,看看哪个好Inception模块将不同大小的卷积核组合在一起,从而有效捕获图像中的各种特征,无论是边缘、纹理还是高级抽象的特征。
GoogleNet的架构包括多个Inception模块,这些模块由卷积层、池化层、全连接层和辅助分类器组成。此外,GoogleNet采用了1x1卷积核来减少模型的参数数量,从而减小了计算复杂度。上图的图例可以看到一些简单的标识,以及在网络中的分布
刘二二人这里提到了一点,观察网络的共同点,发现有一部分出现的频率很大,如下图红框中所示

🍋1×1 convolution
这解释1×1的卷积前,我们先来看看Inception模型图示,不难发现,每条路都有一个共同的点那就是都经过了1×1的卷积。
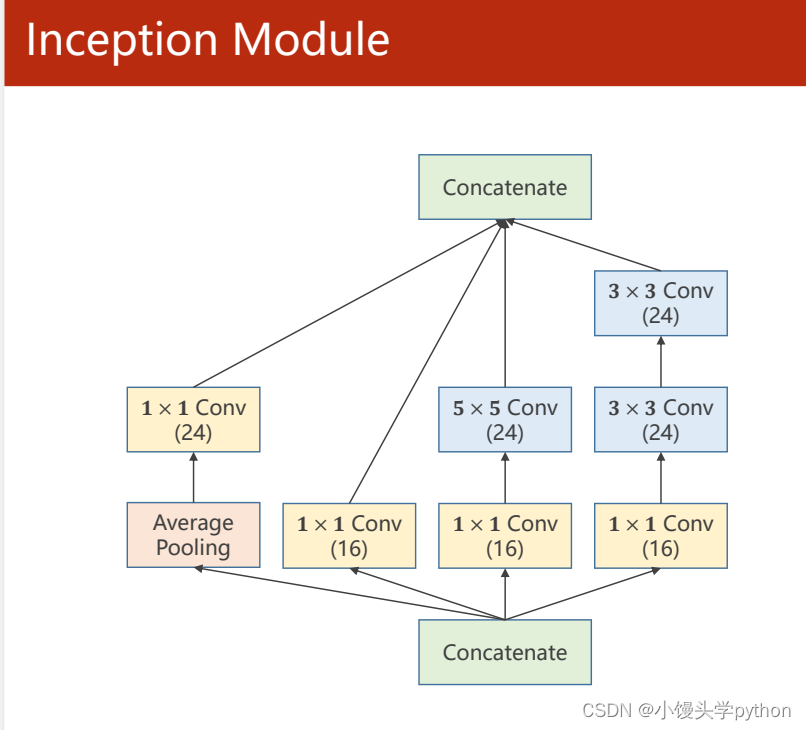
那么1×1的卷积究竟有什么魔力呢?我们先从下方的图示了解一下运算
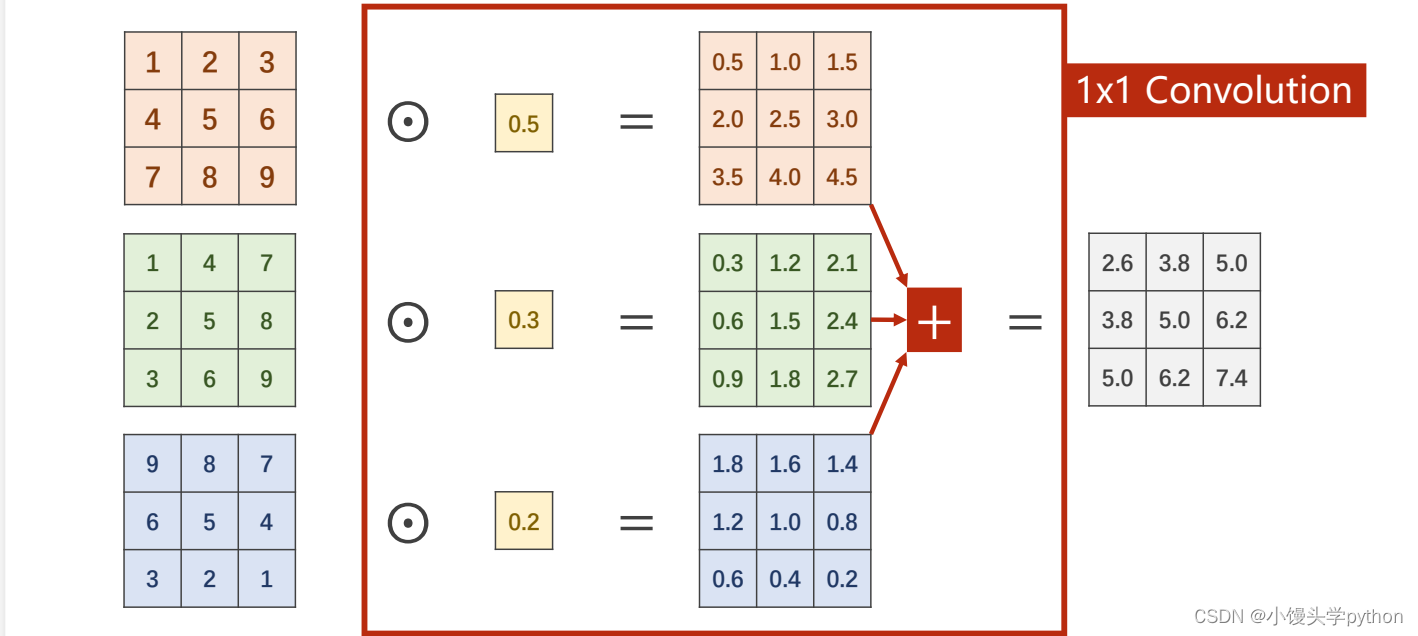
其实就是每个相乘再相加,接下来我们通过一组数据进行对比一下,1×1卷积的作用
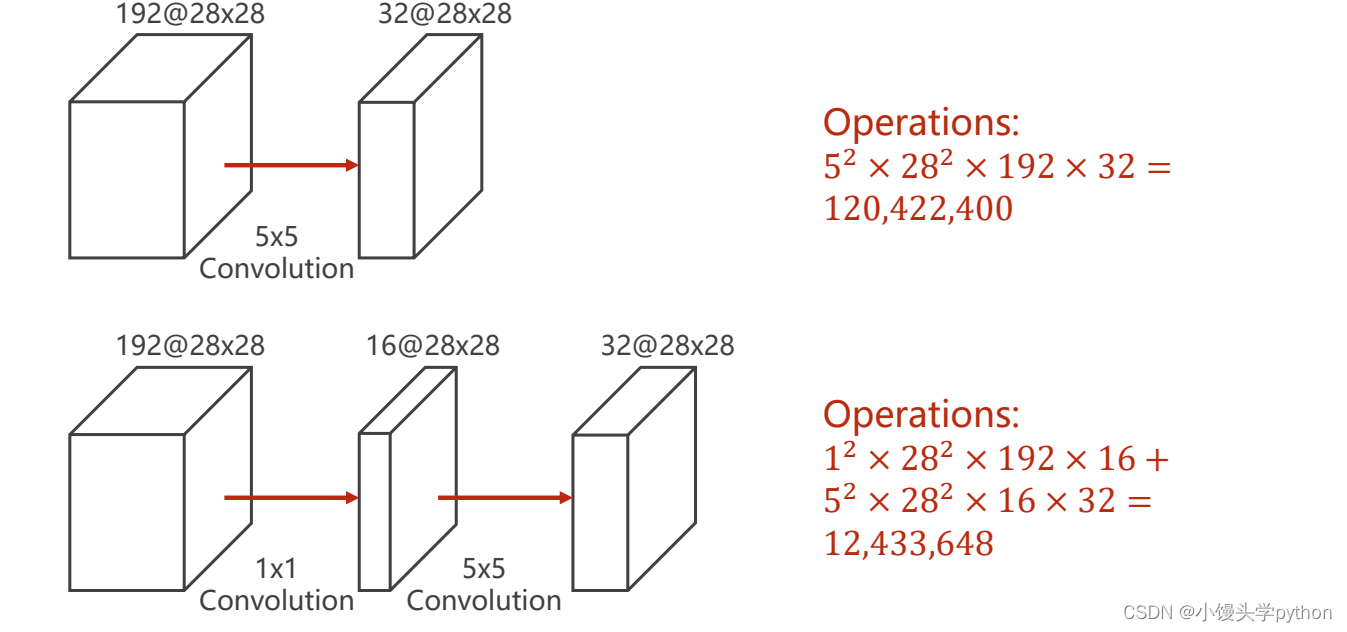
同样都是从192 Channel到32 Channel,前者使用了一个5×5的卷积,后者在5×5的卷积前加了一个1×1的卷积,运算值居然是原来的十分之一,那么从这里我们就清楚了它的主要功能。
-
通道降维(channel dimension reduction):通过应用 1×1 卷积,可以减小特征图的通道数量,从而降低模型的计算负担。这对于减小模型的参数数量和计算复杂度很有帮助。通道降维有时也称为特征压缩。
-
通道混合(channel mixing):1×1 卷积可以将不同通道之间的信息进行混合。它通过学习权重来组合输入通道的信息,以产生更丰富的特征表示。这有助于模型更好地捕获特征之间的关联。
-
非线性变换:虽然 1×1 卷积核的大小为 1x1,但通常会包括非线性激活函数,如ReLU(Rectified Linear Unit)。这使得 1×1 卷积可以执行非线性变换,有助于模型更好地捕获复杂的模式。
如果使用代码进行每条路的编写可以参考下图
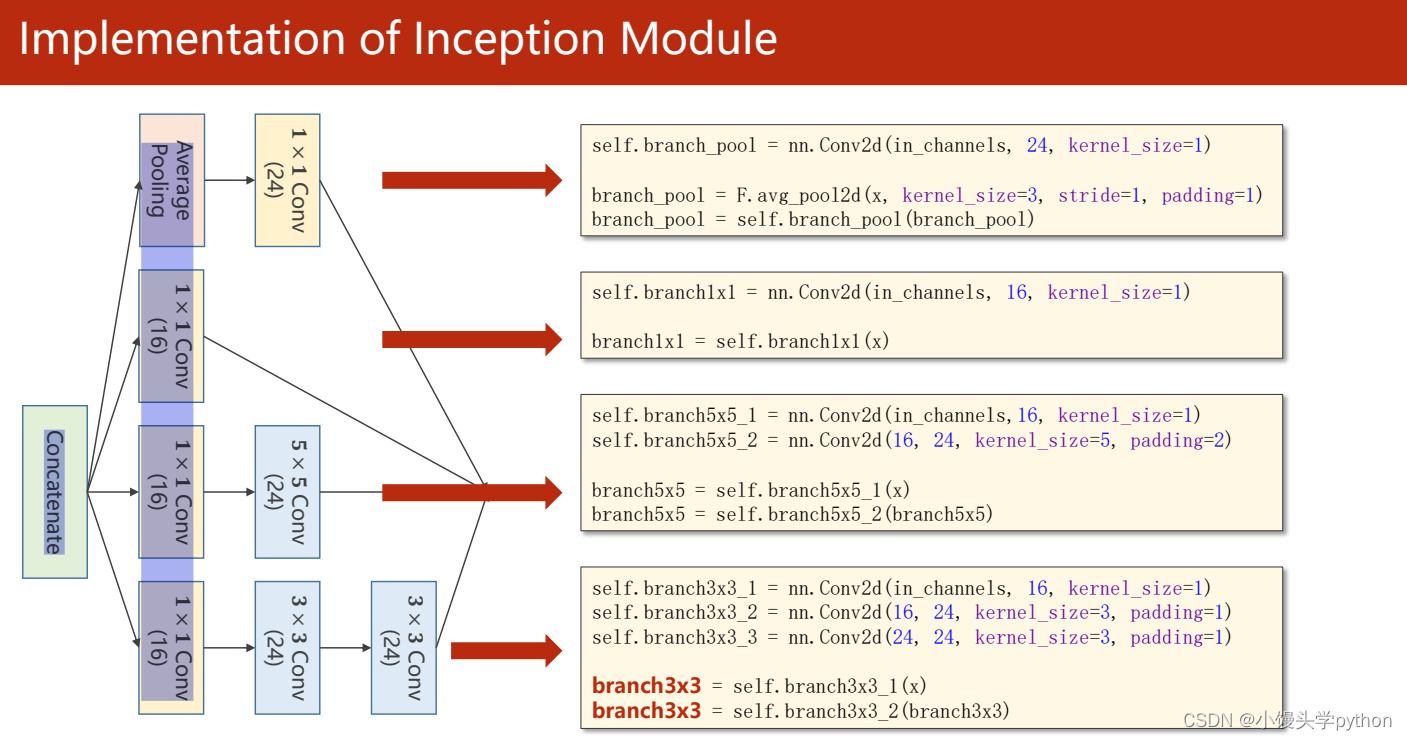
最后一个老师说空间不足,这里需要补充一句
branch3×3 = self.branch3×3_3(branch3×3)
之后需要将它们使用cat拼接起来
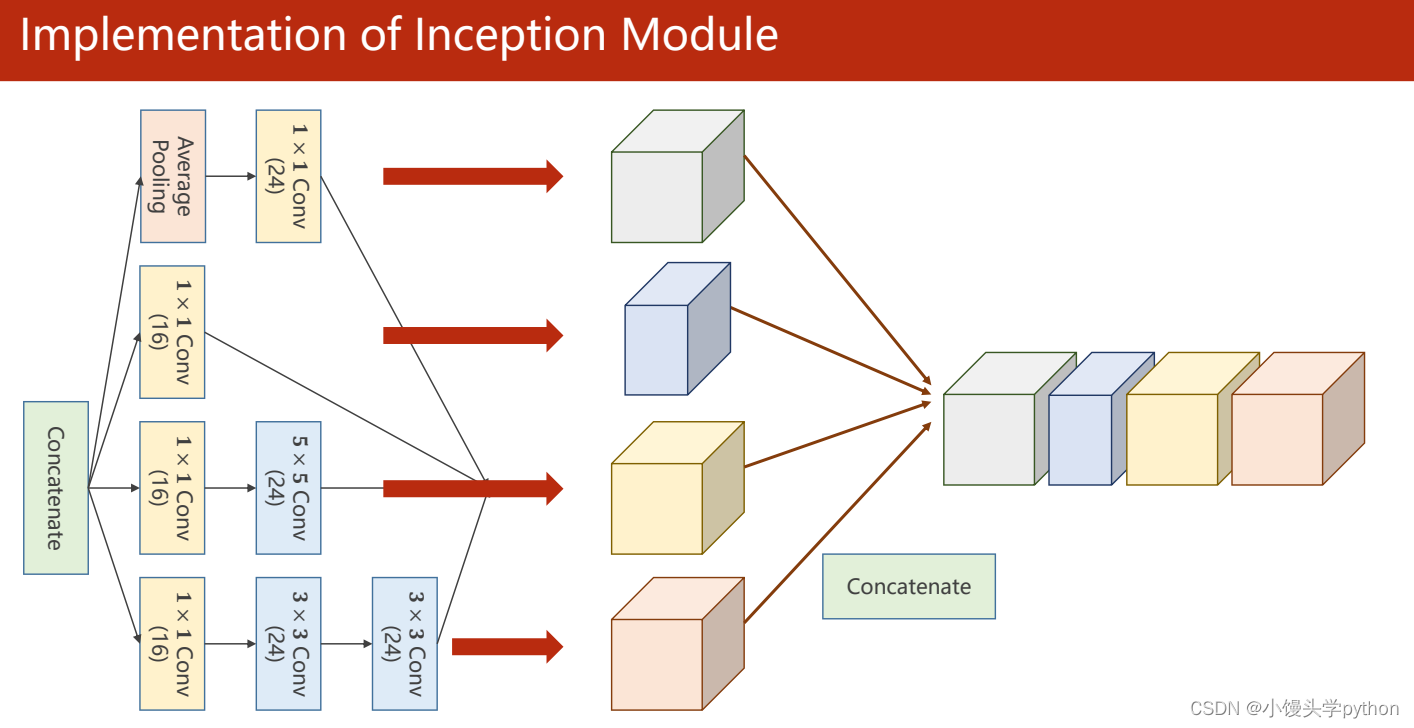
outputs = [branch1x1, branch5x5, branch3x3, branch_pool]
return torch.cat(outputs, dim=1)
这里说明一下拼接的作用,Inception模块中的拼接操作的主要作用是将不同尺度和类型的特征融合在一起,以丰富特征表示并提高网络性能。这是GoogleNet取得成功的一个关键因素,使其在图像分类等任务中表现出色。
完整的代码如下:
class InceptionA(nn.Module):def __init__(self, in_channels):super(InceptionA, self).__init__()self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)self.branch5x5_1 = nn.Conv2d(in_channels,16, kernel_size=1) self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1) self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1) self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)def forward(self, x):branch1x1 = self.branch1x1(x)branch5x5 = self.branch5x5_1(x)branch5x5 = self.branch5x5_2(branch5x5)branch3x3 = self.branch3x3_1(x)branch3x3 = self.branch3x3_2(branch3x3) branch3x3 = self.branch3x3_3(branch3x3)branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1) branch_pool = self.branch_pool(branch_pool)outputs = [branch1x1, branch5x5, branch3x3, branch_pool] return torch.cat(outputs, dim=1)
之后我们需要定义网络层
class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = nn.Conv2d(1, 10, kernel_size=5) self.conv2 = nn.Conv2d(88, 20, kernel_size=5)self.incep1 = InceptionA(in_channels=10) self.incep2 = InceptionA(in_channels=20)self.mp = nn.MaxPool2d(2)self.fc = nn.Linear(1408, 10)def forward(self, x):in_size = x.size(0)x = F.relu(self.mp(self.conv1(x))) x = self.incep1(x)x = F.relu(self.mp(self.conv2(x))) x = self.incep2(x)x = x.view(in_size, -1)x = self.fc(x)return x
🍋如何有效避免梯度消失?
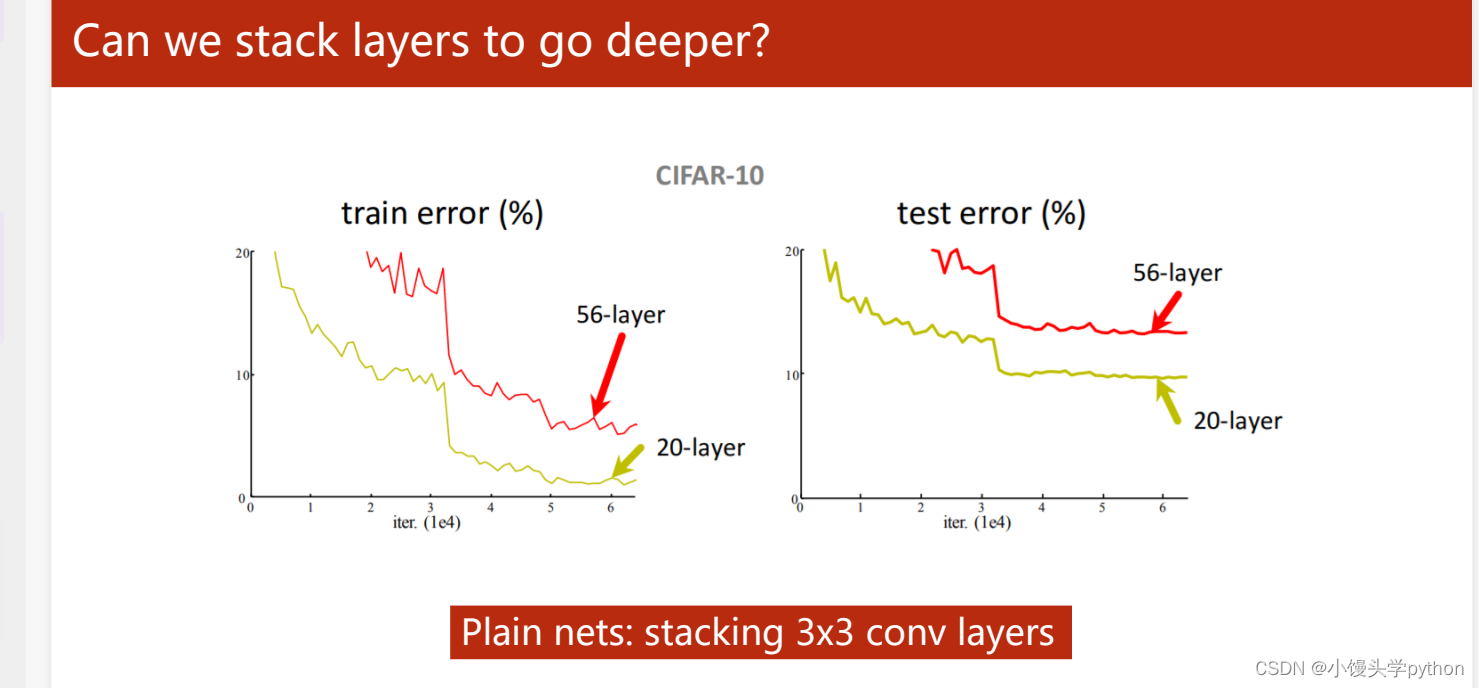
这里我们引入Residual net
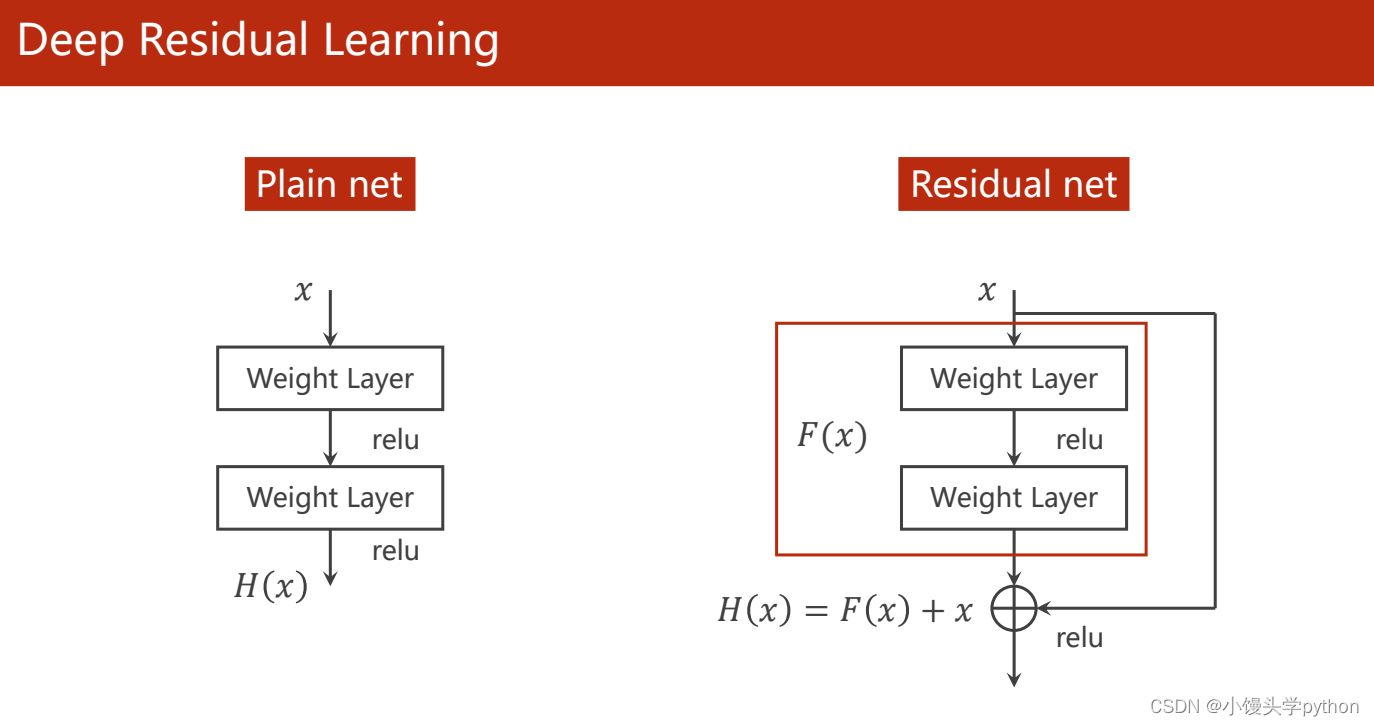
完整的结构与代码如下

🍋总结
GoogleNet是深度学习领域的一项重要成就,它的Inception架构为图像分类和计算机视觉任务提供了高效的解决方案。在Python中,我们可以轻松使用深度学习框架来构建和应用GoogleNet模型。同时文本还介绍了一种避免梯度消失的方法。
视频结尾老师讲述了一些学习方法,主要有四点如下
- 理论《深度学习》
- 阅读pytorch文档(通读一遍)
- 复现经典论文(代码下载,读代码,写代码)
- 扩充视野
本文根据b站刘二大人《PyTorch深度学习实践》完结合集学习后加以整理,文中图文均不属于个人。

挑战与创造都是很痛苦的,但是很充实。
相关文章:

探索未来的视觉革命:卷积神经网络的崭新时代(二)
💗💗💗欢迎来到我的博客,你将找到有关如何使用技术解决问题的文章,也会找到某个技术的学习路线。无论你是何种职业,我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章,也欢…...
博客后台模块续更(三)
四、后台模块-动态路由 实现了这个动态路由功能之后,就能在浏览器web页面登录进博客管理后台了 1. 接口分析 后台系统需要能实现不同的用户权限可以看到不同的功能,即左侧的导航栏 请求方式 请求地址 请求头 GET /getRouters 需要token请求头 …...

第十二届蓝桥杯模拟赛第三期
A填空题 问题描述 请问在 1 到 2020 中,有多少个数与 2020 互质,即有多少个数与 2020 的最大公约数为 1。 参考答案 800 public class Main {public static void main(String[] args) {int ans0;for(int i1;i<2020;i) {if(gcd(2020,i)1) {ans;}}…...

2023年浙大MEM考前80天上岸经验分享
时间过得真快,转眼间已经是十月份了。回想起去年这个时候,我还在为考研而感到焦虑不安。然而,如今我已经在浙大MEM项目学习了一个多月的时间了。在这一个月的学习过程中,我不仅学到了许多专业知识,还结识了很多志同道合…...

增加并行度后,发现Flink窗口不会计算的问题。
文章目录 前言一、现象二、结论三、解决 前言 窗口没有关闭计算的问题,一直困扰了很久,经过多次验证,确定了问题的根源。 一、现象 Flink使用了window,同时使用了watermark ,并且还设置了较高的并行度。生产是设置了…...

使用 JMeter 和 Docker 进行服务存根
用于性能测试的服务存根:简介 随着测试项目的复杂性不断增加,越来越多的被测系统的测试流程受到依赖系统的影响。当我说“依赖系统”时,我指的是: 不受当前开发影响的遗留系统 属于另一个组织的第三方服务 您的组织开发的系统&am…...
《王道计算机考研——操作系统》学习笔记总目录+思维导图
本篇文章是对《王道计算机考研——操作系统》所有知识点的笔记总结归档和计算机网络的思维导图 学习视频:王道计算机考研 操作系统 408四件套【计网、计组、操作系统、数据结构】完整课堂PPT 思维导图 (求Star~):【王道考研】计…...

多模态及图像安全的探索与思考
前言 第六届中国模式识别与计算机视觉大会(The 6th Chinese Conference on Pattern Recognition and Computer Vision, PRCV 2023)已于近期在厦门成功举办。通过参加本次会议,使我有机会接触到许多来自国内外的模式识别和计算机视觉领域的研究…...

基础算法相关笔记
排序 最好情况下: 冒泡排序 最坏时间复杂度 O ( n 2 ) O(n^2) O(n2)。 插入排序 最坏时间复杂度为 O ( n 2 ) O(n^2) O(n2),最优时间复杂度为 O ( n ) O(n) O(n)。 平均情况下: 快速排序 最坏时间复杂度为 O ( n 2 ) O(n^2) O(n2)&…...
Mac电脑无法识别移动硬盘怎么办?
很多人都喜欢在Mac电脑上办公、学习,但有时我们将移动硬盘连接Mac电脑时,却会发现电脑无法识别移动硬盘。那么,Mac电脑无法识别移动硬盘怎么办呢? Mac无法识别移动硬盘的原因 导致Mac不识别移动硬盘的原因有很多,你可…...

14Maven与Tomcat面试题
1MAVEN Maven是一个基于项目对象模型(POM)的项目管理工具,它可以帮助开发者自动化构建、依赖管理、项目报告等。Maven通过一个中央信息片段能够管理项目的构建、报告和文档等步骤,同时也能够管理项目的依赖。Maven的核心概念是POM…...
会议OA小程序【首页布局】
目录 一. Flex布局介绍 1.1 什么是Flex布局 1.2 基本概念 1.3 Flex属性 二. 会议OA首页轮播图的实现 配置 Mock工具 swiper 效果展示 三. 会议OA首页会议信息布局 index.js index.wxml index.wxss 首页整体效果展示 一. Flex布局介绍 布局的传统解决方案&#x…...

高效表达三步
一、高效表达 高效表达定主题搭架子填素材 第一: 1个核心主题,让别人秒懂你的想法 (表达要定主题) 第二: 3种经典框架,帮你快速整理表达思路 第三: 2种表达素材,让发言更具说服力…...

怎样修改ESP32的CPU主频
ESP32的主频默认设置为160mhz,但ESP32最高可以跑到240mhz, 修改方法: idf.py menuconfig --> Component config --> ESP System Settings --> CPU frequency 可以看到三个选项,80,160, 240&…...
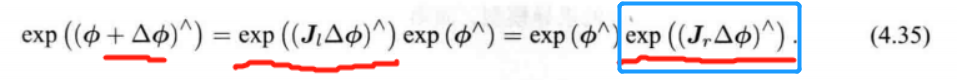
《视觉 SLAM 十四讲》V2 第 10 讲 后端优化2 简化BA 【位姿图】
文章目录 第10讲 后端210.1 滑动窗口滤波 和 优化10.1.2 滑动窗口法 10.2 位姿图10.3 实践: 位姿图优化本讲 CMakeLists.txt 10.3.1 g2o 原生位姿图 【Code】10.3.2 李代数上的位姿优化 【Code】 习题10题1 【没推完】 LaTex 第10讲 后端2 滑动窗口优化 位姿图优化…...

【斗破年番】再遭群嘲,美杜莎怀孕之事被魔改,三方联手除萧潇?
【侵权联系删除】【文/郑尔巴金】 斗破苍穹年番第67集已经更新了。和很多人一样,小郑也去看了,只是小郑万万没有想到,我满怀期待的去看这一集,这一集却能魔改成这样。魔改成什么样了呢?下面来分析下吧! 一&…...

字节面试题——计算机网络,附答案
1.TCP 三次握手和四次挥手 相关面试题: 计算机网络常见面试题总结(上) | JavaGuide(Java面试 学习指南) 为什么要三次握手?第 2 次握手传回了 ACK,为什么还要传回 SYN?为什么要四次挥手?为什么不能把服务器发送的 ACK 和 FIN…...
Flask Web 安装bootstrap失败pip install bootstrap
失败原因:网速太慢了 把公共wifi换成手机热点,成功:) 😃 更新:开了手机热点还是报下面的错,但是把科学上网关了,就成功了,反正就是网络问题...
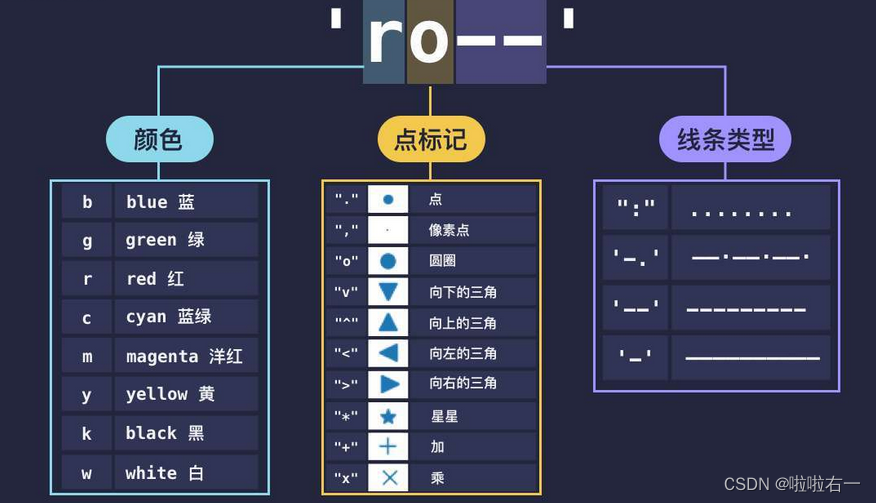
可视化 | python可视化相关库梳理(自用)| pandas | Matplotlib | Seaborn | Pyecharts | Plotly
文章目录 📚Plotly🐇堆叠柱状图🐇环形图🐇散点图🐇漏斗图🐇桑基图🐇金字塔图🐇气泡图🐇面积图⭐️快速作图工具:plotly.express🐇树形图…...
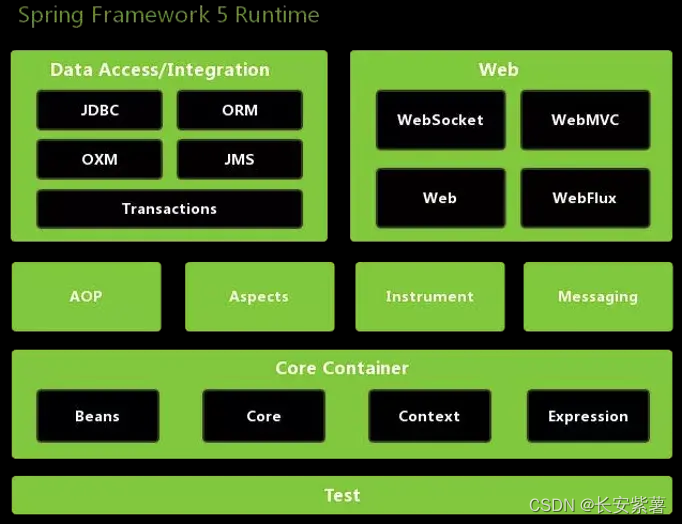
黑豹程序员-架构师学习路线图-百科:Java的第二春Spring框架
文章目录 1、 Spring的发展历史2、为什么Spring能霸屏?2.1、容器的设计2.2、通过四个策略2.3、三种方式 3、学习编程设计的典范 1、 Spring的发展历史 正当SUN公司的EJB在全球开始热炒时,正当程序员纷纷转型EJB开发时,正当程序员为跑通EJB程…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

