模拟退火算法改进
import numpy as np
import matplotlib.pyplot as plt
import math
import random
from scipy.stats import norm
from mpl_toolkits.mplot3d import Axes3D
# 目标函数
def Function(x, y):
return -20 * np.exp(-0.2*np.sqrt(0.5*(x*x+y*y)))\
-np.exp(0.5*(np.cos(2*np.pi*x)+np.cos(2*np.pi*y)))+20+np.e
# 初始化状态
def initN(low, high):
'''
随机生成一组状态取能量最低的状态
:param low:
:param high:
:return:
'''
x = random.uniform(low, high)
y = random.uniform(low, high)
z = Function(x, y)
for i in range(20):
x1 = random.uniform(low, high)
y1 = random.uniform(low, high)
z1 = Function(x1, y1)
if z1 < z:
x = x1
y = y1
z = z1
return x, y
# 绘制目标函数
def figureFuc(low, high):
X = np.linspace(low, high, 500)
Y = np.linspace(low, high, 500)
XX, YY = np.meshgrid(X, Y)
Z = -20 * np.exp(-0.2*np.sqrt(0.5*(XX*XX+YY*YY)))\
-np.exp(0.5*(np.cos(2*np.pi*XX)+np.cos(2*np.pi*YY)))+20+np.e
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(XX, YY, Z, cmap=plt.get_cmap('rainbow'))
plt.show()
# Metropolis准则接受新解
def Metropolis(detaF, T): # detaF为f(n+1) - f(x)
if detaF < 0:
return 1
else:
pTk = math.exp(-detaF/T)
if pTk > random.random():
return 1
else:
return 0
# 利用正态分布产生新解
def get_normal_random_number(x,y,scale): # 正态分布
'''
:param x: 均值
:param y: 均值
:param scale: 方差
:return:
'''
fx = np.random.normal(x, scale)
x = norm.ppf(fx)
fy = np.random.normal(y, scale)
y = norm.ppf(fy)
return x, y
# 利用均匀分布产生新解
def get_uniform_random_number(low, high):
'''
:param low:
:param high:
:return:
'''
x = np.random.uniform(low, high)
y = np.random.uniform(low, high)
return x, y
# 冷却函数
def descT(T, k):
# return T/np.log(1 + k)
return 0.9*T
# 主函数
def startMain():
# 初始化
low = -5
high = 5
T = 10000
Tmin = 10
k = 1
# figureFuc(low, high) # 画图
#x = random.uniform(low, high)
#y = random.uniform(low, high)
x, y = initN(low, high)
z = Function(x, y)
min_value = z
record_value = [] # 用数组记录被接受的新解并绘图,方便分析
while(T > Tmin and k <= 1000):
x1, y1 = get_normal_random_number(x, y, 2) # 利用正态分布产生新解
# x1, y1 = get_uniform_random_number(low, high) # 利用随机分布产生新解
if x1 < low or x1 > high or y1 < low or y1 > high: # 新解不在定义域内时跳出本次循环
break
z1 = Function(x1, y1) # 计算新解的目标函数值
deltaE = z1 - z
min_value = min(min_value, z1)
if Metropolis(deltaE, T) == 1: # 接受按照Metropolis准则接受新解
x = x1
y = y1
z = z1
record_value.append(z)
if deltaE > 0:
T = descT(T, k)
else:
k += 1
print('迭代到组后的解:', z)
print('记录下的最优解:', min_value)
# 打印解的变化曲线
x=[i+1 for i in range(len(record_value))]
plt.plot(x, record_value)
plt.show()
if __name__ == "__main__":
startMain()
相关文章:

模拟退火算法改进
import numpy as np import matplotlib.pyplot as plt import math import random from scipy.stats import norm from mpl_toolkits.mplot3d import Axes3D # 目标函数 def Function(x, y): return -20 * np.exp(-0.2*np.sqrt(0.5*(x*xy*y)))\ -np.exp(0.5*(n…...
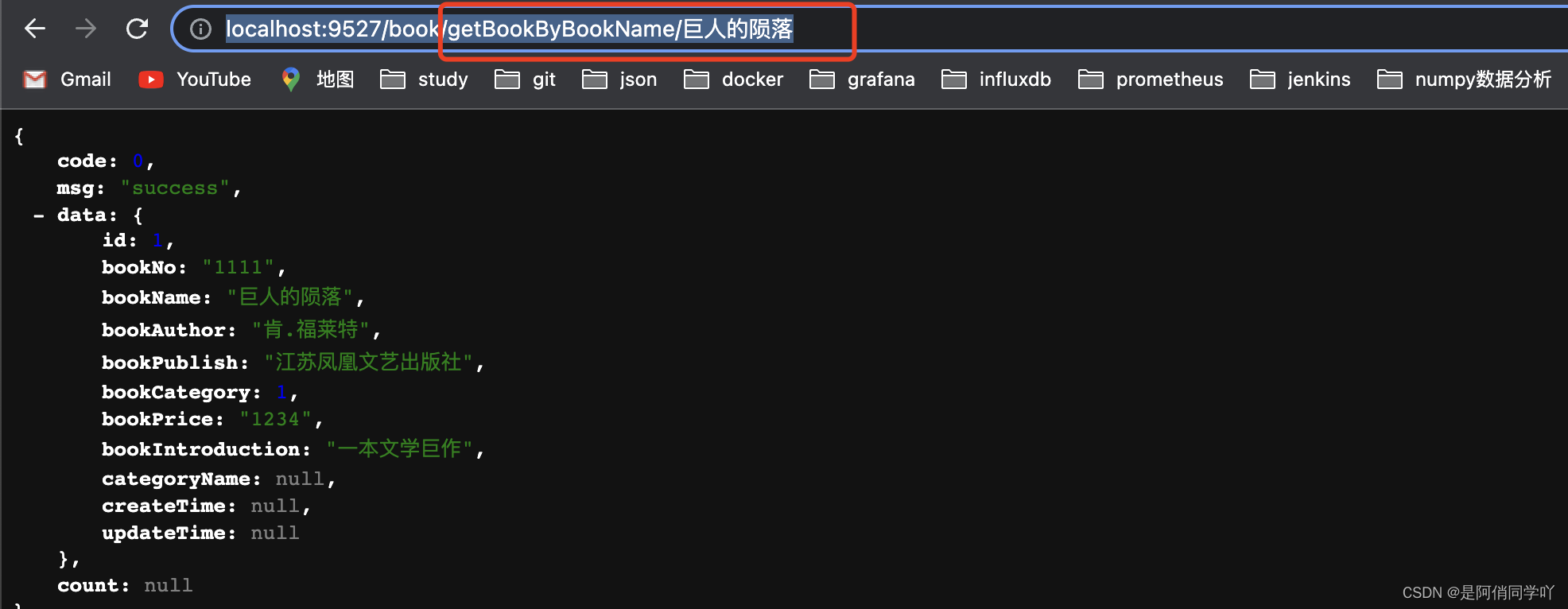
SpringBoot+HttpClient+JsonPath提取A接口返回值作为参数调用B接口
前言 在做java接口自动化中,我们常常需要依赖多个接口,A接口依赖B,C,D接口的响应作为请求参数;或者URL中的参数是从其他接口中提取返回值作获取参数这是必不可少的。那么怎么实现呢?下面就来介绍多业务依赖…...

JUC 之 CompletableFuture
——CompletableFuture Future Future 接口(FutureTask 实现类) 定义了操作异步任务执行的一些方法,如获取异步的执行结果、取消任务的执行、判断任务是否被取消、判断任务执行是否完毕例如: 主线程让一个子线程去执行任务&…...

7-vue-1
谈谈你对MVVM的理解 为什么要有这些模式,目的:职责划分、分层(将Model层、View层进行分类)借鉴后端思想,对于前端而已,就是如何将数据同步到页面上 MVC模式 代表:Backbone underscore jquer…...
OpenAPI SDK组件介绍
背景 公司成立以来,积累了数以万计的可复用接口。上层的SaaS业务,原则上要复用这些接口开发自己的业务,为了屏蔽调用接口的复杂性,基础服务开发了apisdk组件,定义了一套声明OpenAPI的注解、注解解析器,实例…...

【Java】Synchronized锁原理和优化
一、synchronized介绍 synchronized中文意思是同步,也称之为”同步锁“。 synchronized的作用是保证在同一时刻, 被修饰的代码块或方法只会有一个线程执行,以达到保证并发安全的效果。 synchronized是Java中解决并发问题的一种最常用的方法…...
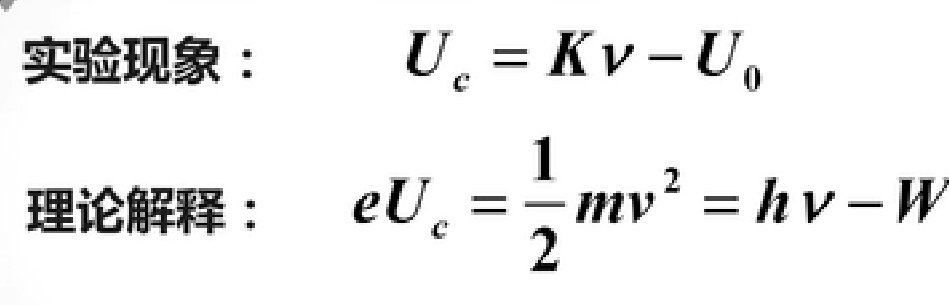
西北工业大学2020-2021学年大物(I)下期末试题选填解析
2 位移电流。磁效应服从安培环路,热效应不服从焦耳-楞次定律。注意,它是变化的电场而非磁场产生。3 又考恒定磁场中安培环路定理。4感生电场5 麦克斯韦速率分布函数。6 相同的高温热源和低温热源之间的一切可逆热机的工作效率相等,无论工质如…...

PHP - ChatGpt API 接入 ,代码,亲测!(最简单!)
由于最近ChatGpt 大火,但是门槛来说是对于大家最头疼的环节, 我自己也先开发了一个个人小程序!大家可以访问使用下, 由此ChatGpt 有一个API 可以仅供大伙对接 让我来说下资质: 1:首先要搞得到一个 ChatGp…...
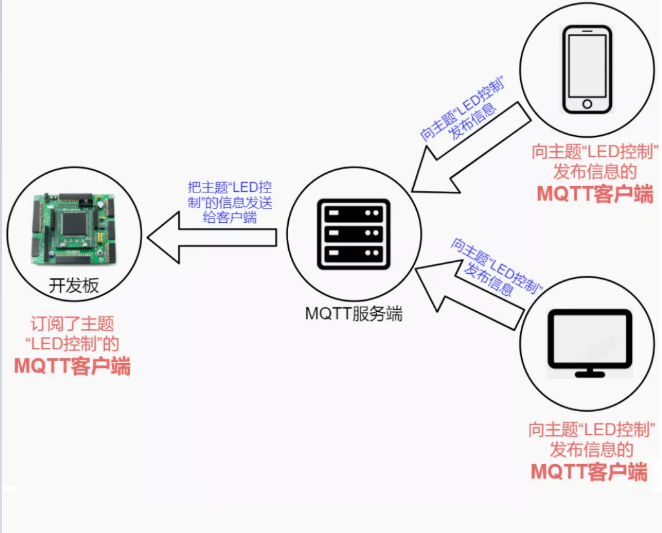
物联网MQTT协议简单介绍
物联网曾被认为是继计算机、互联网之后,信息技术行业的第三次浪潮。随着基础通讯设施的不断完善,尤其是 5G 的出现,进一步降低了万物互联的门槛和成本。物联网本身也是 AI 和区块链应用很好的落地场景之一,各大云服务商也在纷纷上…...
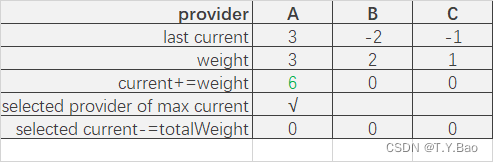
Dubbo 源码解读:负载均衡策略
概览 org.apache.dubbo包下META-INF/dubbo/internal/org.apache.dubbo.rpc.cluster.LoadBalance中内部spi实现类有以下几种: randomorg.apache.dubbo.rpc.cluster.loadbalance.RandomLoadBalance roundrobinorg.apache.dubbo.rpc.cluster.loadbalance.RoundRobinL…...
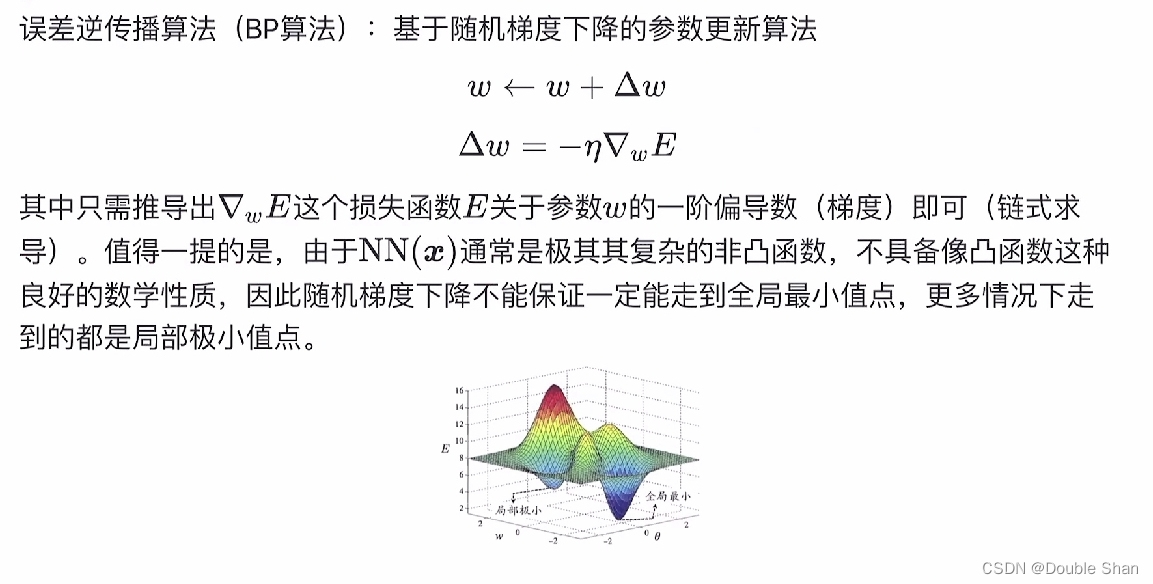
吃瓜教程笔记—Task04
神经网络 知识点 M-P神经元 模型如图所示: 神经元的工作机理:神经元接收来到n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值将与神经元的阈值进行比较,然后通过…...
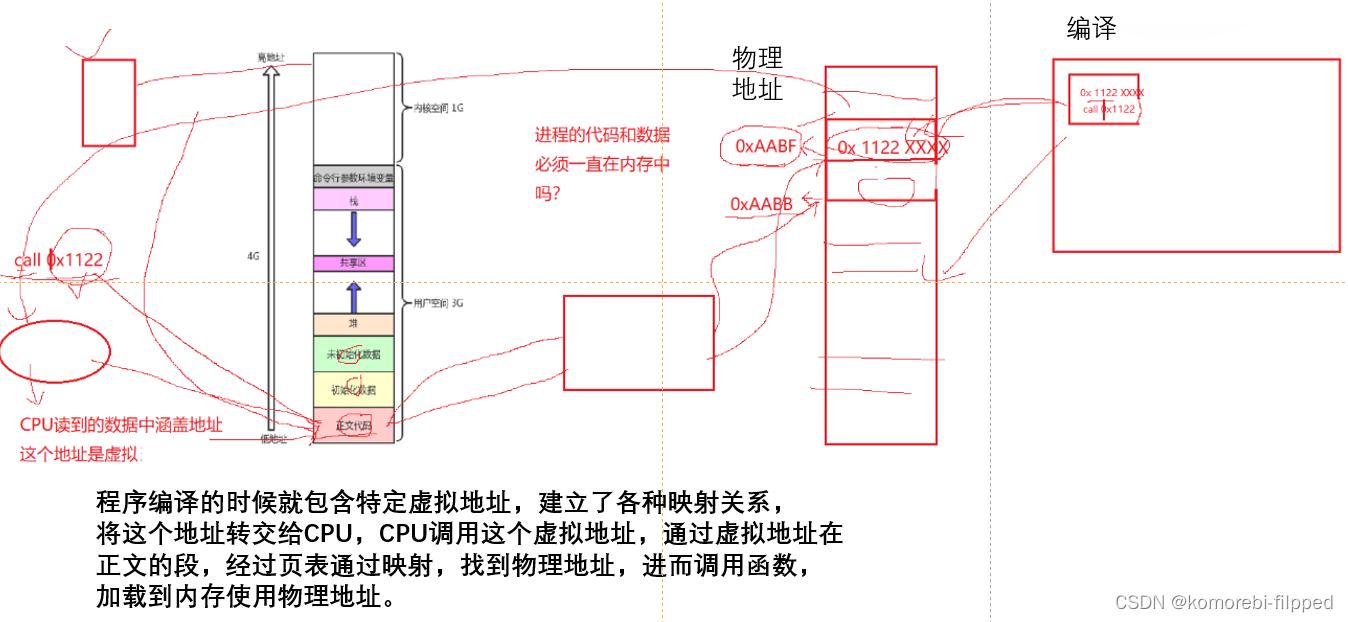
进程地址空间(虚拟地址空间)
目录 引入问题 测试代码 引入地址空间 故事1: 故事二: 解决问题 为什么有虚拟地址空间 扩展 扩展1(没有地址空间,OS如何工作) 扩展2 (代码只读深入了解) 扩展3(malloc本质…...

【项目精选】基于Vue + ECharts的数据可视化系统的设计与实现(论文+源码+视频)
今天给小伙伴们推荐一款超优秀的全新Vue3.0大数据系统Vue3-bigData。 点击下载源码 vue3-bigdata 基于vue3.0echarts构建的可视化大屏图表展示系统。包括各种可视化图表及Vue3新API使用。 功能 柱状图、饼图、词云图、漏斗图 水球图、折线图 仪表盘、雷达图 矩形树图、关系…...

JavaScript Window Screen
文章目录JavaScript Window ScreenWindow ScreenWindow Screen 可用宽度Window Screen 可用高度JavaScript Window Screen window.screen 对象包含有关用户屏幕的信息。 Window Screen window.screen对象在编写时可以不使用 window 这个前缀。 一些属性: screen…...

【双重注意机制:肺癌:超分】
Dual attention mechanism network for lung cancer images super-resolution (肺癌图像超分辨率的双重注意机制网络) 目前,肺癌的发病率和死亡率均居世界恶性肿瘤之首。提高肺部薄层CT的分辨率对于肺癌筛查的早期诊断尤为重要。针对超分辨…...

各种中间件的使用
init background 这一部分我们学习一些常用的, 但是不需要深入理解的中间件 , 例如kafka ,分布式文件系统。 summary Content what is kafka? What time to used it ? 其实消息队列就是解决系统之间复杂交互例如聊天系统和交易系统, …...

Systemverilog覆盖率的合并和计算方式
在systemverilog中,对于一个covergroup来说,可能会有多个instance,我们可能需要对这些instance覆盖率进行操作。 只保存covergroup type的覆盖率,不需要保存instance-specified的覆盖率coverage type和instance-specified的覆盖率…...

(周末公众号解读系列)2000字-视觉SLAM综述
参考链接:https://mp.weixin.qq.com/s?__bizMzg2NzUxNTU1OA&mid2247528395&idx1&sn6c9290dd7fd926f11cbaca312fbe99a2&chksmceb84202f9cfcb1410353c805b122e8df2e2b79bd4031ddc5d8678f8b11c356a25f55f488907&scene126&sessionid1677323905…...

力扣29-两数相除
29. 两数相除 给你两个整数,被除数 dividend 和除数 divisor。将两数相除,要求 不使用 乘法、除法和取余运算。 整数除法应该向零截断,也就是截去(truncate)其小数部分。例如,8.345 将被截断为 8 &#x…...
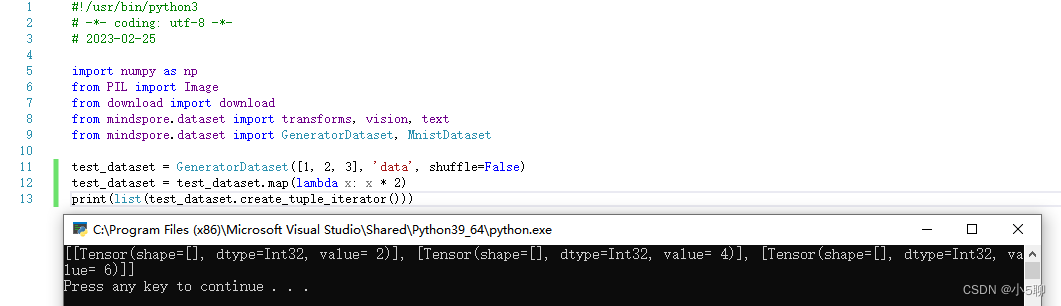
【MindSpore】安装和使用MindSpore 2.0.0版本简单实现数据变换Transforms功能
本篇文章主要是讲讲MindSpore的安装以及根据官方提供的例子实现数据变换功能。 昇思MindSpore是一款开源的AI框架,旨在实现易开发、高效执行、全场景覆盖三大目标。 目录1、加入MindSpore社区2、安装前准备2.1、获取安装命令2.2、安装pip2.3、确认系统环境3、安装Mi…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
