神经网络的梯度优化方法
神经网络的梯度优化是深度学习中至关重要的一部分,它有助于训练神经网络以拟合数据。下面将介绍几种常见的梯度优化方法,包括它们的特点、优缺点以及原理。
-
梯度下降法 (Gradient Descent):
- 特点: 梯度下降是最基本的优化算法,它试图通过迭代更新参数来最小化损失函数。
- 优点:
- 简单易懂。
- 全局收敛性(在凸优化问题中)。
- 缺点:
- 可能收敛速度慢,特别是对于高度非凸的问题。
- 学习率的选择通常需要仔细调整。
- 原理: 参数更新规则如下,其中 η \eta η 是学习率:
θ t + 1 = θ t − η ∇ J ( θ t ) \theta_{t+1} = \theta_{t} - \eta \nabla J(\theta_t) θt+1=θt−η∇J(θt)
-
随机梯度下降法 (Stochastic Gradient Descent, SGD):
- 特点: SGD在每个训练样本上执行参数更新,适用于大型数据集。
- 优点:
- 更快的收敛速度,通常能够在局部最小值附近摆动,有助于跳出局部最小值。
- 可以处理大型数据集。
- 缺点:
- 参数更新噪音较大,不稳定。
- 原理: 参数更新规则如下,其中 η \eta η 是学习率, i i i 表示随机选取的样本索引:
θ t + 1 = θ t − η ∇ J ( θ t ; x i , y i ) \theta_{t+1} = \theta_t - \eta \nabla J(\theta_t; x_i, y_i) θt+1=θt−η∇J(θt;xi,yi)
-
批量梯度下降法 (Mini-Batch Gradient Descent):
- 特点: MBGD是一种折中方法,每次使用一小批量训练数据进行参数更新。
- 优点:
- 收敛速度通常比纯SGD更快。
- 噪音相对较小。
- 缺点:
- 仍然需要手动调整学习率。
- 原理: 参数更新规则如下,其中 η \eta η 是学习率, B B B 表示批量大小:
θ t + 1 = θ t − η 1 B ∑ i = 1 B ∇ J ( θ t ; x i , y i ) \theta_{t+1} = \theta_t - \eta \frac{1}{B} \sum_{i=1}^{B} \nabla J(\theta_t; x_i, y_i) θt+1=θt−ηB1i=1∑B∇J(θt;xi,yi)
-
动量梯度下降 (Momentum):
- 特点: 动量法引入了动量项,有助于加速收敛并减小震荡。
- 优点:
- 加速收敛,特别对于高曲率的损失函数。
- 减小震荡,有助于避免局部最小值。
- 缺点:
- 需要调整动量参数。
- 原理: 参数更新规则如下,其中 η \eta η 是学习率, β \beta β 是动量系数:
v t + 1 = β v t + ( 1 − β ) ∇ J ( θ t ) v_{t+1} = \beta v_t + (1 - \beta) \nabla J(\theta_t) vt+1=βvt+(1−β)∇J(θt)
θ t + 1 = θ t − η v t + 1 \theta_{t+1} = \theta_t - \eta v_{t+1} θt+1=θt−ηvt+1
-
自适应学习率方法 (Adaptive Learning Rate Methods):
- 特点: 这类方法根据参数更新的情况自适应地调整学习率。
- 优点:
- 自适应性,通常无需手动调整学习率。
- 缺点:
- 可能较复杂,不稳定。
- 原理: 代表性方法包括Adagrad、RMSprop、Adam等。以Adam为例,参数更新规则如下,其中 η \eta η是学习率, β 1 \beta_1 β1和 β 2 \beta_2 β2是衰减系数:
m t = β 1 m t − 1 + ( 1 − β 1 ) ∇ J ( θ t ) m_t = \beta_1 m_{t-1} + (1 - \beta_1) \nabla J(\theta_t) mt=β1mt−1+(1−β1)∇J(θt)
v t = β 2 v t − 1 + ( 1 − β 2 ) ( ∇ J ( θ t ) ) 2 v_t = \beta_2 v_{t-1} + (1 - \beta_2) (\nabla J(\theta_t))^2 vt=β2vt−1+(1−β2)(∇J(θt))2
m ^ t = m t 1 − β 1 t \hat{m}_t = \frac{m_t}{1 - \beta_1^t} m^t=1−β1tmt
v ^ t = v t 1 − β 2 t \hat{v}_t = \frac{v_t}{1 - \beta_2^t} v^t=1−β2tvt
θ t + 1 = θ t − η v ^ t + ϵ ⊙ m ^ t \theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \odot \hat{m}_t θt+1=θt−v^t+ϵη⊙m^t
不同的优化方法适用于不同的问题,选择哪种方法通常需要根据具体情况和经验来决定。当在深度学习中选择梯度优化方法时,常常需要进行超参数调整和实验来找到最佳性能。
相关文章:

神经网络的梯度优化方法
神经网络的梯度优化是深度学习中至关重要的一部分,它有助于训练神经网络以拟合数据。下面将介绍几种常见的梯度优化方法,包括它们的特点、优缺点以及原理。 梯度下降法 (Gradient Descent): 特点: 梯度下降是最基本的优化算法,它试图通过迭代…...

linux 装机教程(自用备忘)
文章目录 安装 pyenv 管理多版本 python 环境安装使用使用 pyenv 和 virtualenv 管理虚拟 python 环境 vscode 连接远程服务器tmux 美化zsh 安装 pyenv 管理多版本 python 环境 安装 (教程参考:https://www.modb.pro/db/155036) sudo apt-…...
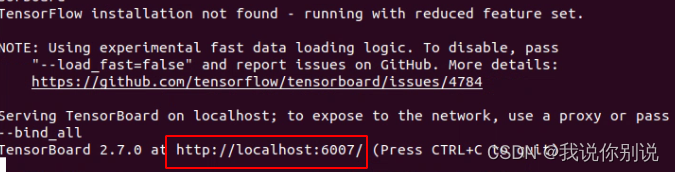
Tensorboard安装及简单使用
Tensorboard 1. tensorboard 简单介绍2. 安装必备环境3. Tensorboard安装4. 可视化命令 1. tensorboard 简单介绍 TensorBoard是一个可视化的模块,该模块功能强大,可用于深度学习网络模型训练查看模型结构和训练效果(预测结果、网络模型结构…...
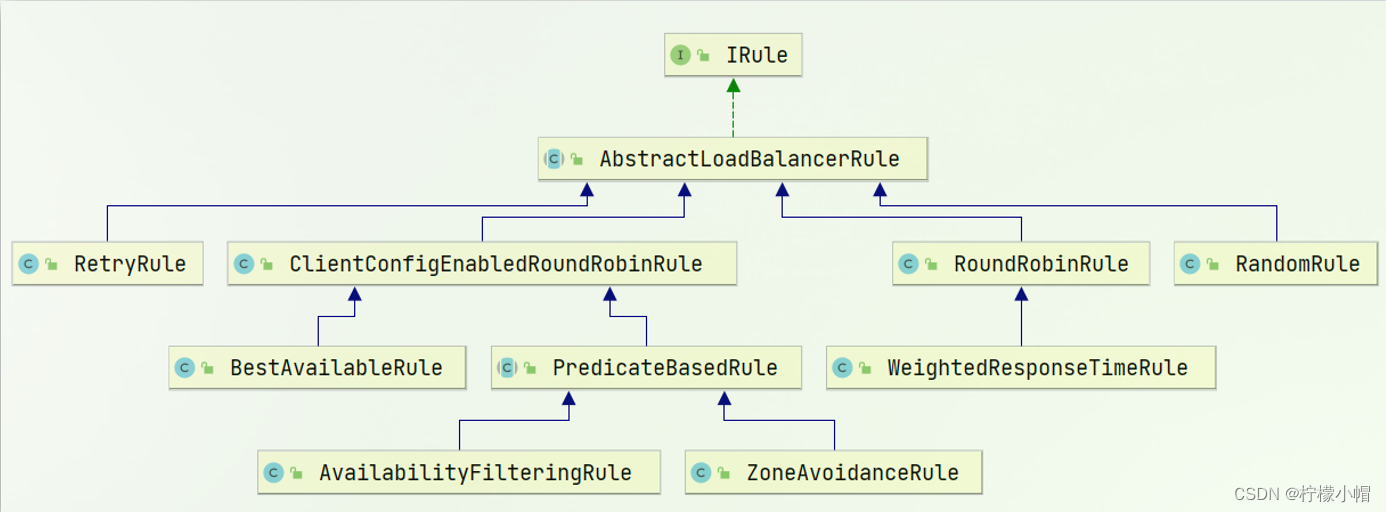
SpringCloud 微服务全栈体系(二)
第三章 Eureka 注册中心 假如我们的服务提供者 user-service 部署了多个实例,如图: 思考几个问题: order-service 在发起远程调用的时候,该如何得知 user-service 实例的 ip 地址和端口?有多个 user-service 实例地址…...

flutter 常用组件:列表ListView
文章目录 总结#1、通过构造方法直接构建 ListView 提供了一个默认构造函数 ListView,我们可以通过设置它的 children 参数,很方便地将所有的子 Widget 包含到 ListView 中。 不过,这种创建方式要求提前将所有子 Widget 一次性创建好,而不是等到它们真正在屏幕上需要显示时才…...
十四天学会C++之第七天:STL(标准模板库)
1. STL容器 什么是STL容器,为什么使用它们。向量(vector):使用向量存储数据。列表(list):使用列表实现双向链表。映射(map):使用映射实现键值对存储。 什么…...
Linux 下安装 miniconda,管理 Python 多环境
安装 miniconda 1、下载安装包 Miniconda3-py37_22.11.1-1-Linux-x86_64.sh,或者自行选择版本 2、把安装包上传到服务器上,这里放在 /home/software 3、安装 bash Miniconda3-py37_22.11.1-1-Linux-x86_64.sh 4、按回车 Welcome to Miniconda3 py37…...
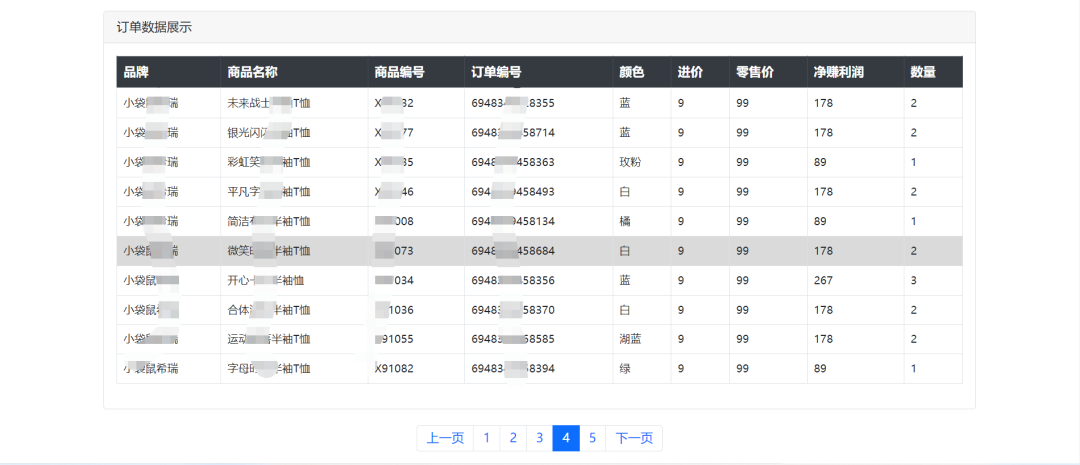
Django和jQuery,实现Ajax表格数据分页展示
1.需求描述 当存在重新请求接口才能返回数据的功能时,若页面的内容很长,每次点击一个功能,页面又回到了顶部,对于用户的体验感不太友好,我们希望当用户点击这类的功能时,能直接加载到数据,请求…...
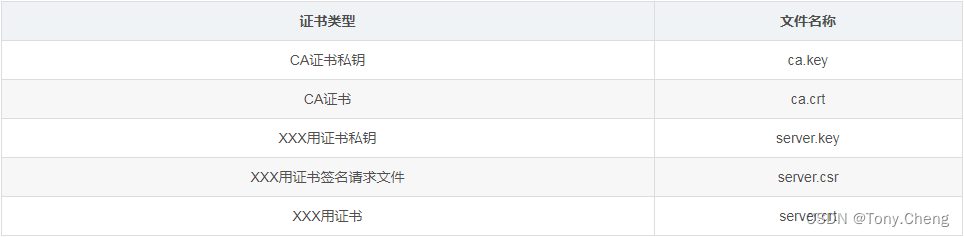
k8s认证
1. 证书介绍 服务端保留公钥和私钥,客户端使用root CA认证服务端的公钥 一共有多少证书: *Etcd: Etcd对外提供服务,要有一套etcd server证书Etcd各节点之间进行通信,要有一套etcd peer证书Kube-APIserver访问Etcd&a…...
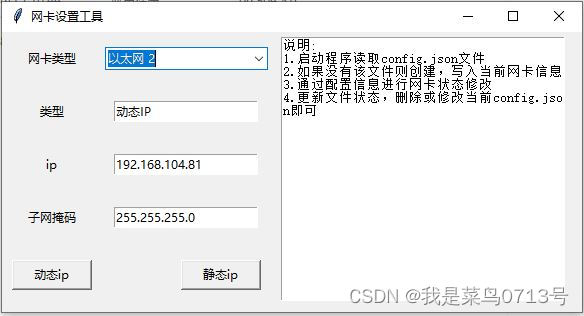
基于python开发的IP修改工具
工作中调试设备需要经常修改电脑IP,非常麻烦,这里使用Pythontkinter做了一个IP修改工具 说明: 1.启动程序读取config.json文件2.如果没有该文件则创建,写入当前网卡信息3.通过配置信息进行网卡状态修改4.更新文件状态,删除或修…...
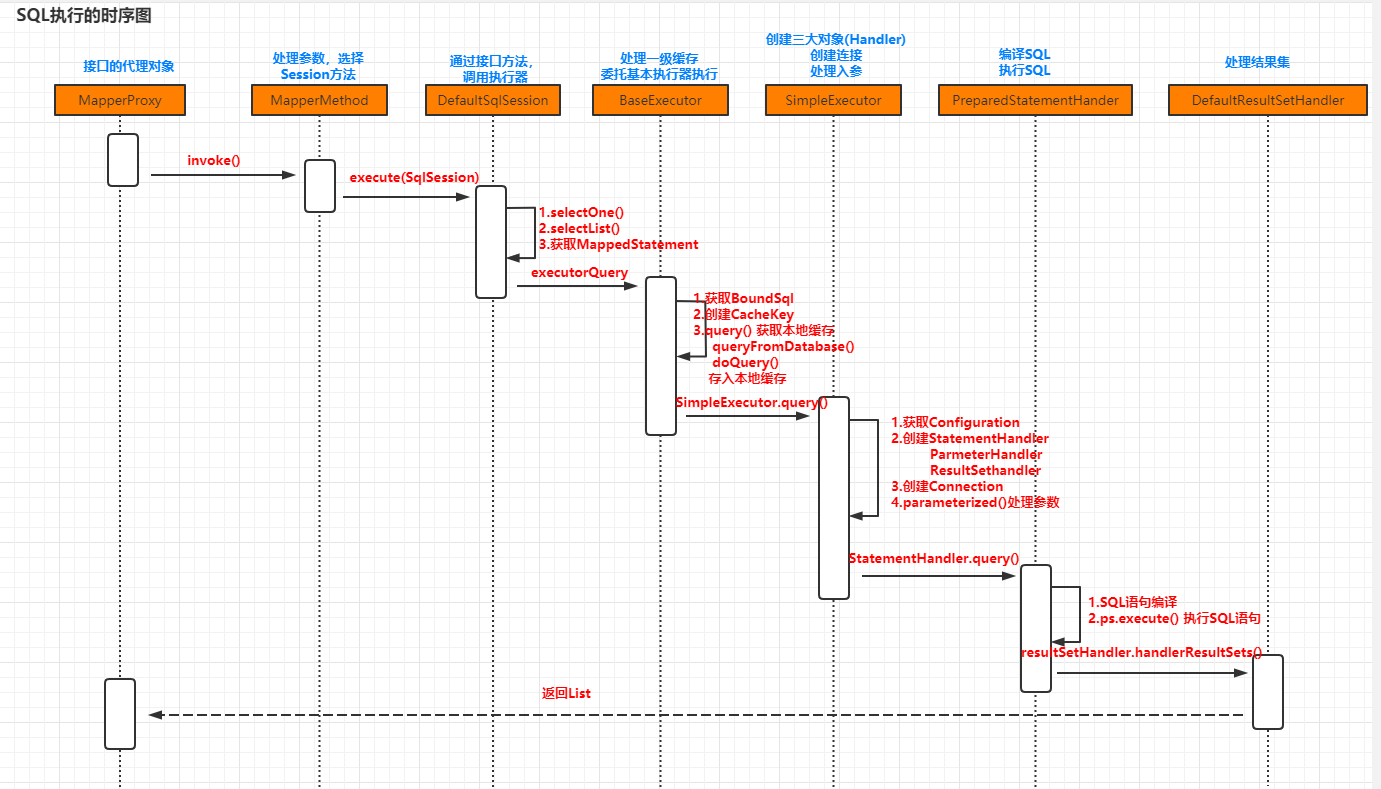
Mybatis源码分析
1. Mybatis整体三层设计 SSM中,Spring、SpringMVC已经在前面文章源码分析总结过了,Mybatis源码相对Spring和SpringMVC而言是的简单的,只有一个项目,项目下分了很多包。从宏观上了解Mybatis的整体框架分为三层,分别是基…...
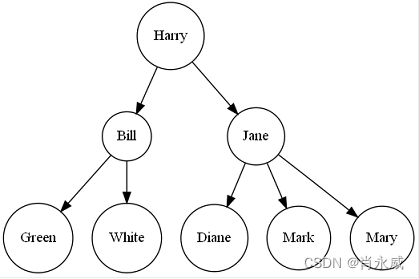
python树结构包treelib入门及其计算应用
树是计算机科学中重要的数据结构。例如决策树等机器学习算法设计、文件系统索引等。创建treelib包是为了在Python中提供树数据结构的有效实现。 Treelib的主要特点包括: 节点搜索的高效操作。支持常见的树操作,如遍历、插入、删除、节点移动、浅/深复制…...
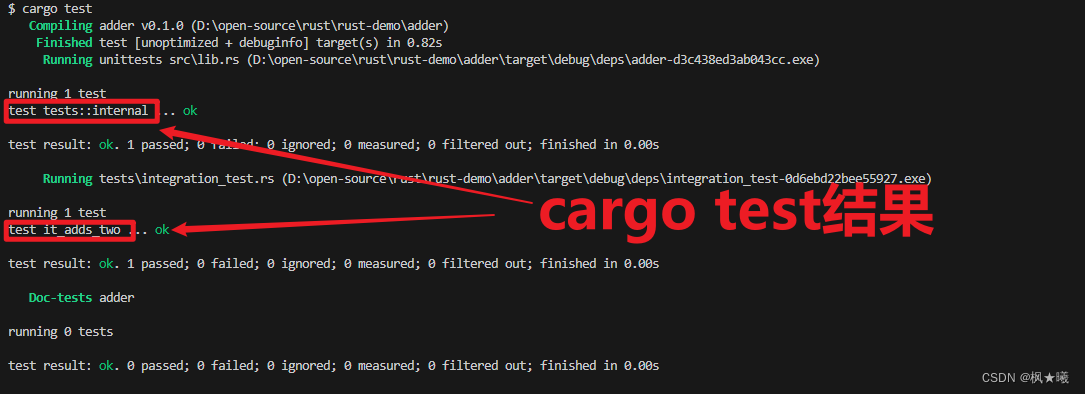
Rust之自动化测试(三): 测试组合
开发环境 Windows 10Rust 1.73.0 VS Code 1.83.1 项目工程 这里继续沿用上次工程rust-demo 测试组合 正如本章开始时提到的,测试是一个复杂的学科,不同的人使用不同的术语和组织。Rust社区根据两个主要类别来考虑测试:单元测试和集成测试。单元测试很…...
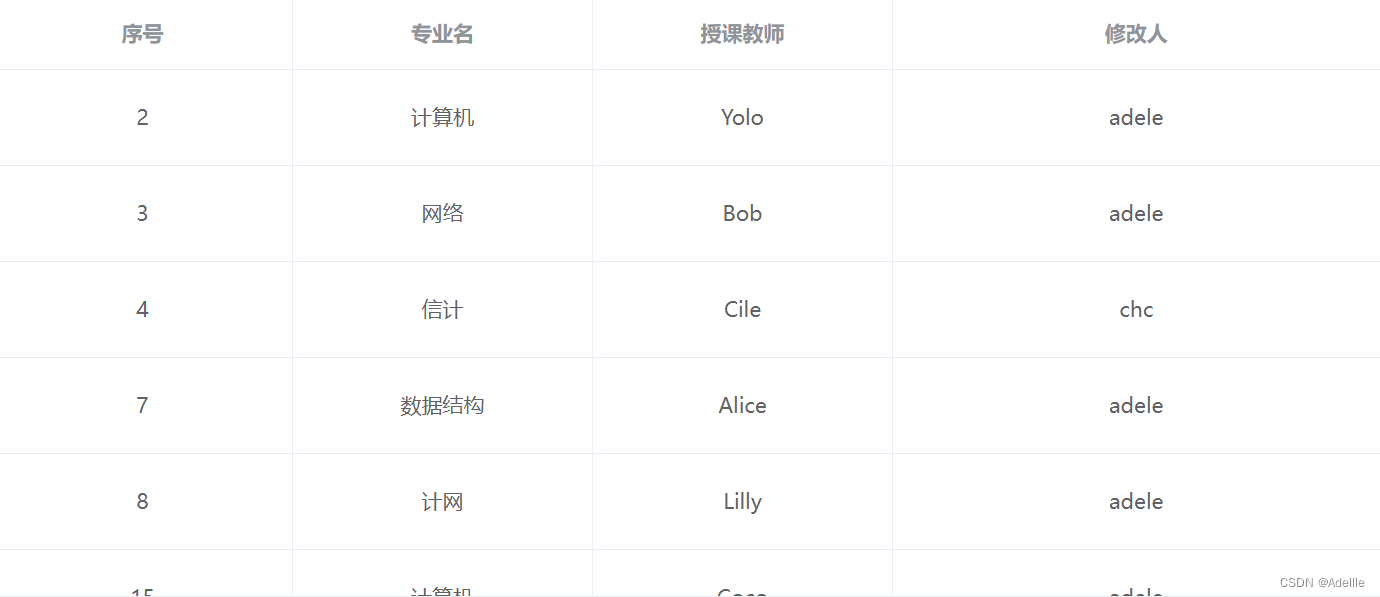
专业管理菜单的增删改、查重
1,点击专业管理菜单------查询所有专业信息列表 ①点击菜单,切换专业组件 ②切换到列表组件后,向后端发送请求到Servlet ③调用DAO层,查询数据库(sql),封装查询到的内容 ④从后端向前端做出…...

vue3插件开发,上传npm
创建插件 在vue3工程下,创建组件vue页: toolset.vue。并设置组件名称。注册全局组件。新建index.js文件。内容如下,可在main.js中引入index.js,注册该组件进行测试。
python【多线程、单线程、异步编程】三个版本--在爬虫中的应用
并发编程在爬虫中的应用 之前的课程,我们已经为大家介绍了 Python 中的多线程、多进程和异步编程,通过这三种手段,我们可以实现并发或并行编程,这一方面可以加速代码的执行,另一方面也可以带来更好的用户体验。爬虫程…...

大模型LLM相关面试题整理-位置编码-tokenizer-激活函数-layernorm
10 LLMs 位置编码篇 10.1.1 什么是位置编码? 位置编码是一种用于在序列数据中为每个位置添加位置信息的技术。在自然语言处理中,位置编码通常用于处理文本序列。由于传统的神经网络无法直接捕捉输入序列中的位置信息,位置编码的引入可以帮助…...

python在nacos注册微服务
安装 首先需要安装python的nacos sdk pip install nacos-sdk-python 注册 注册过程非常简单,需要注意的是,注册完要定时发送心跳,否则服务会被nacos删掉。 import nacos import timeSERVER_ADDRESSES "http://1.2.3.4:8848" …...
tuxera ntfs2024破解版mac电脑磁盘读写软件
大家都知道由于操作系统的原因,在苹果电脑上不能够读写NTFS磁盘,但是,今天小编带来的这款tuxera ntfs 2024 mac版,完美的解决了这个问题。这是一款在macOS平台上使用的磁盘读写软件,能够实现苹果Mac OS X系统读写Micro…...

【源码】C++坦克大战源码
文章目录 题目介绍你收到的所有文件源码效果展示报告内容 题目介绍 代码量:1450 语言:C 你收到的所有文件 其中一个是devc版本,也可以用visual stdio 运行。 源码效果展示 typedef struct //这里的出现次序指的是一个AI_ta…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...
