2023年9月青少年软件编程(C 语言) 等级考试试卷(三级)
2023年9月青少年软件编程(C 语言) 等级考试试卷(三级)含答案
1.谁是你的潜在朋友
题目描述
“臭味相投”——这是我们描述朋友时喜欢用的词汇。两个人是朋友通常意味着他们存在着许多共同的兴趣。然而作为一个宅男,你发现自己与他人相互了解的机会并不太多。幸运的是,你意外得到了一份北大图书馆的图书借阅记录,于是你挑灯熬夜地编程,想从中发现潜在的朋友。 首先你对借阅记录进行了一番整理,把N个读者依次编号为1,2,…,N,把M本书依次编号为1,2,…,M。同时,按照“臭味相投”的原则,和你喜欢读同一本书的人,就是你的潜在朋友。你现在的任务是从这份借阅记录中计算出每个人有几个潜在朋友。
输入
第一行两个整数N,M,2 <= N ,M<= 200。接下来有N行,第i(i = 1,2,…,N)行每一行有一个数,表示读者i-1最喜欢的图书的编号P(1<=P<=M)
输出
包括N行,每行一个数,第i行的数表示读者i有几个潜在朋友。如果i和任何人都没有共同喜欢的书,则输出“BeiJu”(即悲剧,^ ^)
样例输入
4 5
2
3
2
1
样例输出
1
BeiJu
1
BeiJu
参考答案
#include<iostream>
using namespace std;
int n,m;
int a[300];
int main() {cin>>n>>m;for(int i=0;i<n;i++) {cin>>a[i];}for(int i=0;i<n;i++) {int sum=0;for(int j=0;j<n;j++) {if(a[i]==a[j]&&i!=j) {sum++;}}if(sum!=0) {cout<<sum<<endl;} else {cout<<"BeiJu"<<endl;}}return 0;
}
2.课程冲突
题目描述
小 A 修了 n 门课程, 第 i 门课程是从第 ai 天一直上到第 bi 天。
定义两门课程的冲突程度为 : 有几天是这两门课程都要上的。
例如 a1=1,b1=3,a2=2,b2=4 时, 这两门课的冲突程度为 2。
现在你需要求的是这 n 门课中冲突程度最大的两门课的冲突程度。
输入
第一行一个正整数 n 表示课程数量。 接下来 n 行,每行两个正整数 ai,bi。 2 ≤ n≤ 1000, 1 ≤ ai ≤ bi ≤ 1000。
输出
输出一个整数表示最大的冲突程度
样例输入
3
1 3
2 4
5 5
样例输出
2
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
struct project {int start;int end;project(int a,int b):start(a),end(b){}bool operator <(const project A)const {if (start == A.start)return end < A.end;elsereturn start < A.start;}
};
int main() {int n;cin >> n;vector<project>alls;for (int i = 0; i < n; i++){int a, b;cin >> a >> b;alls.push_back(project(a, b));}sort(alls.begin(), alls.end());int result = 0;for (int i = 0; i < n; i++) {if (alls[i].end - alls[i].start < result)//剪枝continue;for (int j = i + 1; j < n; j++) {if (alls[j].start > alls[i].end)break;int t = min(alls[i].end, alls[j].end) - alls[j].start + 1;result = max(t, result);}}cout << result << endl;return 0;
}更多内容请查看网站:【试卷中心 -- C/C++ 三级】
网站链接
青少年软件编程历年真题模拟题实时更新
相关文章:
 等级考试试卷(三级))
2023年9月青少年软件编程(C 语言) 等级考试试卷(三级)
2023年9月青少年软件编程(C 语言) 等级考试试卷(三级)含答案 1.谁是你的潜在朋友 题目描述 “臭味相投”——这是我们描述朋友时喜欢用的词汇。两个人是朋友通常意味着他们存在着许多共同的兴趣。然而作为一个宅男,你…...

用节点亲和性把 Pod 分配到节点
用节点亲和性把 Pod 分配到节点 当前集群信息: rootk8s-master:~# kubectl get node -o wide NAME STATUS ROLES AGE VERSION INTERNAL-IP EXTERNAL-IP OS-IMAGE KERNEL-VERSION CONTAINER-RUNTIME k8s…...
GB28181学习(十)——视音频文件下载
要求 SIP服务器接收到媒体接收者发送的视音频文件下载请求后向媒体流发送者发送媒体文件下载命令,媒体流发送者采用RTP将视频流传输给媒体流接收者,媒体流接收者直接将视频流保存为媒体文件;媒体流接收者或SIP服务器可通过配置查询等方式获取…...
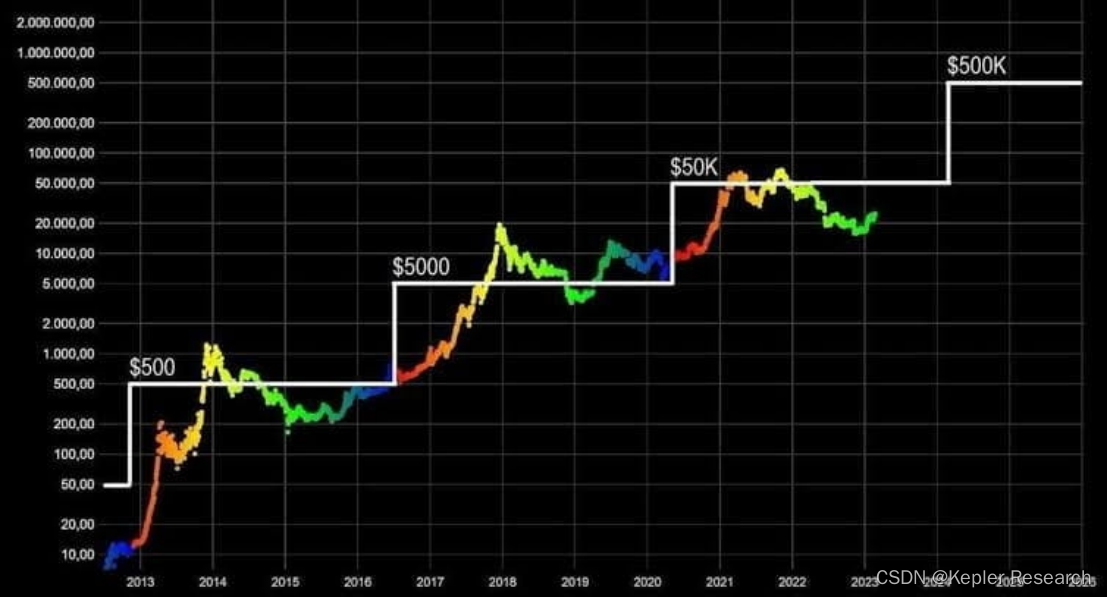
2023 年和 2024 年 10 个最佳加密货币趋势
1.熊市低迷 加密货币市场已进入持续数月的长期看跌阶段。尽管 2023 年初出现了一些看涨走势,但大多数领先的加密货币随后都出现了看跌低迷,导致其市值大幅下跌。 此外,持续的熊市可归因于一系列因素,包括宏观经济不确定性、利率…...

0026【Edabit ★☆☆☆☆☆】Convert Hours and Minutes into Seconds
0026【Edabit ★☆☆☆☆☆】Convert Hours and Minutes into Seconds language_fundamentals math Instructions Write a function that takes two integers (hours, minutes), converts them to seconds, and adds them. Examples convert(1, 3) // 3780 convert(2, 0) //…...
Java 枚举类
一、枚举类简介 1、枚举类概念 类的对象只有有限个且确定的,这种类称之为枚举类;因为在jdk1.5之前没有enum关键字来定义枚举类,只能采用class定义一个类然后将类做一些修改满足对象个数有限且确定,那么这种类就是枚举类…...
SQL sever中的存储过程
在Oracle的专篇中我也有仔细总结了存储过程的相关内容, 文章链接:http://t.csdnimg.cn/Z8AnH 尽管Oracle和SQL sever之间是存在一些区别,但许多基本的概念和原则在Oracle和SQL Server之间是通用的。它们之间有一些常见的区别,如下…...
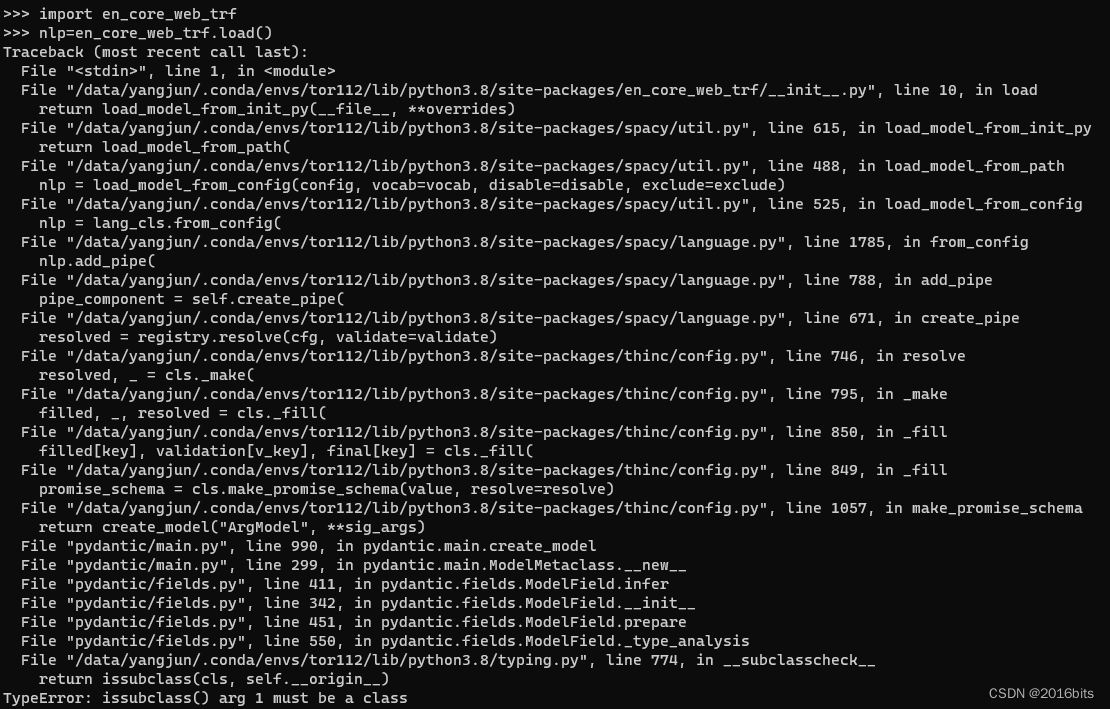
spacy.load(“en_core_web_trf“)报错TypeError: issubclass() arg 1 must be a class
使用spacy时遇到的问题 写在最前面: 安装spacy和en_core_web_trf时需要保证二者版本一致 安装及查看对应spacy版本 安装 pip install spacy查看版本 import spacy spacy.__version__安装en_core_web_trf 直接安装(如果可以的话) pytho…...
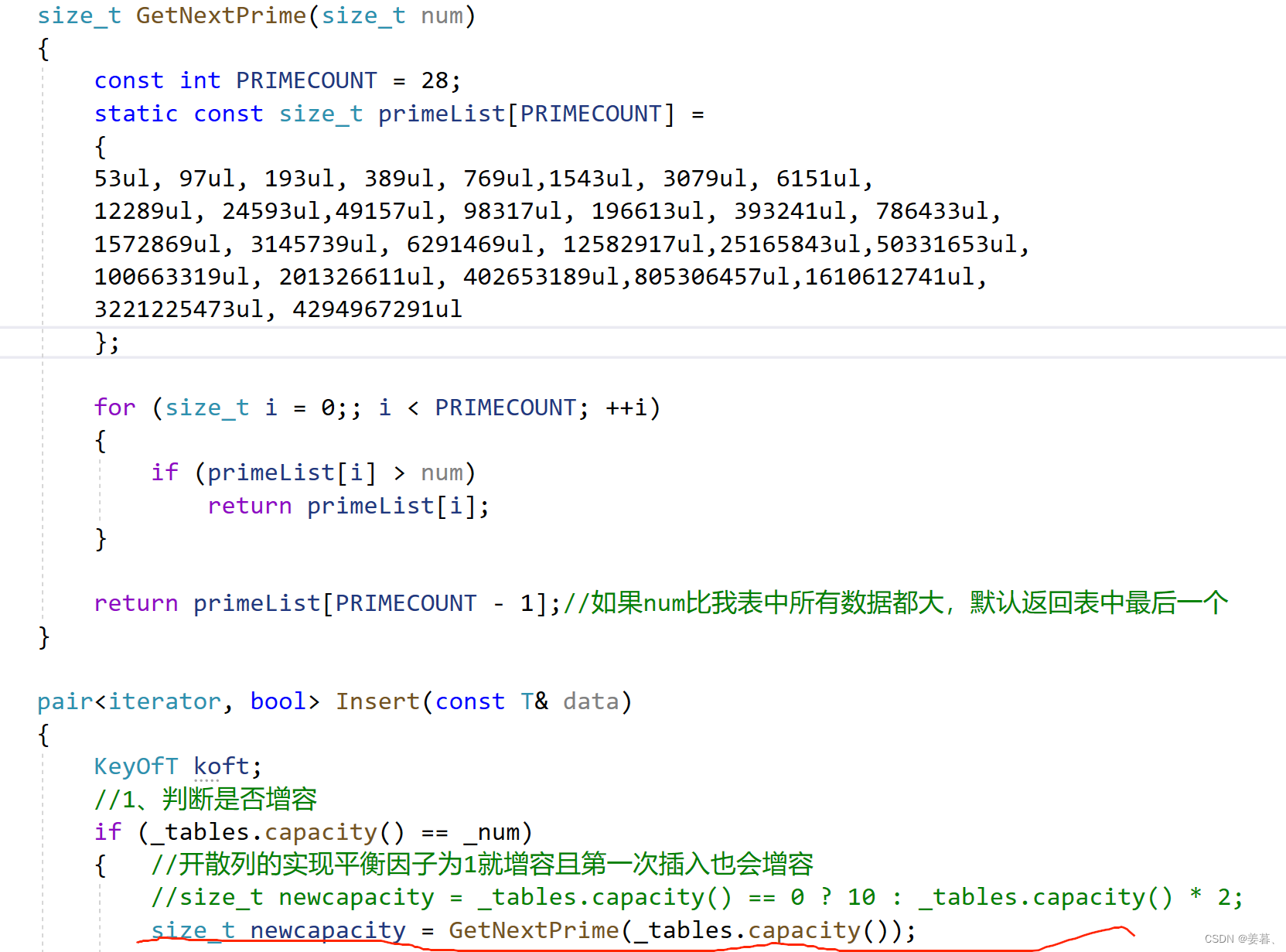
【C++和数据结构】模拟实现哈希表和unordered_set与unordered_map
目录 一、哈希的概念与方法 1、哈希概念 2、常用的两个哈希函数 二、闭散列的实现 1、基本结构: 2、两种增容思路 和 插入 闭散列的增容: 哈希表的插入: 3、查找 4、删除 三、开散列的实现 1、基本结构 2、仿函数Hash 3、迭代器…...

十四天学会C++之第五天:类的详细讨论
1. 友元函数和友元类 什么是友元函数和友元类,它们的作用。如何声明和使用友元函数和友元类,访问类的私有成员。 友元函数(Friend Functions) 友元函数是一种特殊的函数,它被允许访问类的私有成员。这意味着即使成员…...

字典树学习笔记
trie 树,即字典树,是一种可以实现 O ( S ) O(S) O(S) 的预处理( S S S 为所有字符串的长度和), O ( N ) O(N) O(N)( N N N 为查询的字符串的长度)的查询的数据结构。 举个栗子,对于…...

web各个指标理解
QPS : 单位时间得请求次数 TPS :单位时间得事务数 并发 : QPS *单位响应时间 pv :进入一个网站,又单击打开该网站的其他页面,每打开一个页面就 增加一个PV,甚至在同一页面每刷新一次也多一个PV 二八定律:百…...
-- 在gitee上部署远程仓库,通过idea上传本地代码(用idea2022版本开发))
Java后端开发(七)-- 在gitee上部署远程仓库,通过idea上传本地代码(用idea2022版本开发)
目录 1. 在Gitee上创建gitee远程仓库 2.在打开idea,再打开您要上传的idea代码,先创建 本地git仓库...

Go语言入门心法(十二): GORM映射框架
Go语言入门心法(一): 基础语法 Go语言入门心法(二): 结构体 Go语言入门心法(三): 接口 Go语言入门心法(四): 异常体系 Go语言入门心法(五): 函数 Go语言入门心法(六): HTTP面向客户端|服务端编程 Go语言入门心法(七): 并发与通道 Go语言入门心法(八): mysql驱动安装报错o…...

Ubuntu更新镜像源切换
概述 用ubuntu用apt命令,自动安装或更新包的时候,默认的镜像源服务器非常卡,很不方便。切换到国内的镜像源,下载更新非常快。为防止以后忘记,本文以国内服务器阿里巴巴的为例简单描述。 版本 Ubuntu23.10 找到更新…...
“一键合并剪辑,轻松添加片头——全新的视频编辑工具让你成为视频制作达人“
在日常生活中,我们时常会遇到需要制作视频的情况。但面对繁琐的视频剪辑和合并,你是否感到无从下手?今天,我们为你带来一款全新的视频编辑工具,让你轻松成为视频制作达人! 首先我们要进入好简单批量智剪主页…...

1.3 矩阵
一、向量与矩阵 下面是三个向量 u \boldsymbol u u、 v \boldsymbol v v、 w \boldsymbol w w: u [ 1 − 1 0 ] v [ 0 1 − 1 ] w [ 0 0 1 ] \boldsymbol u\begin{bmatrix}\,\,\,\,1\\-1\\\,\,\,\,0\end{bmatrix}\kern 10pt\boldsymbol v\begin{bmatrix}\,\,\,…...

阿里云-AnalyticDB【分析型数据库】总结介绍
一、背景 随着企业IT和互联网系统的发展,产生了越来越多的数据。数据量的积累带来了质的飞跃,使得数据应用从业务系统的一部分演变得愈发独立。物流、交通、新零售等越来越多的行业需要通过OLAP做到精细化运营,从而调控生产规则、运营效率、企…...

数二思维导图
高数上 第一章:函数、极限、连续 函数 函数的单调性、周期性、奇偶性复合函数 极限 求直接代入型的极限求∞∞型的极限用等价无穷小代换求00型的极限用洛必达法则求00型或∞∞型的极限求∞•0型的极限求幂指函数的极限函数的左右极限及需要求左右极限的情形极限的…...
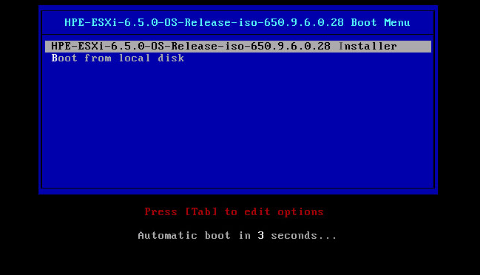
ESXI6.5安装教程
设置从IPMI Virtual Disk 3000启动,出现如下界面: 默认选择第一项,回车安装 安装程序正在检测服务器硬件信息,如果不满足系统安装条件会跳出错误提示。 检测完成之后会出现下面界面 回车 按F11 这里列出了服务器硬盘信息&#…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
