数二思维导图
高数上
第一章:函数、极限、连续
-
函数
- 函数的单调性、周期性、奇偶性
- 复合函数
-
极限
- 求直接代入型的极限
- 求∞∞型的极限
- 用等价无穷小代换求00型的极限
- 用洛必达法则求00型或∞∞型的极限
- 求∞•0型的极限
- 求幂指函数的极限
- 函数的左右极限及需要求左右极限的情形
- 极限的拆分
- 无穷小的比较
- 无穷小与函数极限之间的关系
- 利用极限的保号性判定极值点
- 求函数图像的渐近线
- 利用夹逼定理求数列极限
- 证明单调有界数列的极限存在(上)
- 证明单调有界数列的极限存在(中)
- 证明单调有界数列的极限存在(下)
-
连续
- 证明连续、已知连续求未知参数
- 零点定理
- 介值定理推论
- 间断点
第二章:一元函数微分学
- 第一课判断函数在某点的可导性
- 第二课一般函数求导
- 第三课隐函数求导
- 第四课求高阶导数
- 第五课利用导数定义求极限
- 第六课参数方程求导
- 第七课反函数求导
- 第八课求函数的极值
- 第九课求函数的最值
- 第十课求函数图像的凹凸区间、拐点
- 第十一课求函数图像在某点处的切线方程、法线方程
- 第十二课单调区间、极值点、凹凸区间、拐点、切线斜率在函数
- 第十三课根据已知的变化率求变化率
- 第十四课利用单调性比较大小
- 第十五课证明不等式
- 第十六课利用拉格朗日中值定理证明函数不等式
- 第十七课利用函数图像的凹凸性证明函数不等式
- 第二十课利用单调性求根的个数
- 第二十一课利用罗尔定理推论求根的个数
- 第二十二课微分中值定理(上)
- 第二十三课微分中值定理(中)
- 第二十四课微分中值定理(下)
- 第二十五课泰勒公式
- 第二十六课利用泰勒公式证明不等式
第三章:一元函数积分学
- 第一课求简单的不定积分
- 第二课用第一类换元法计算不定积分
- 第三课用第二类换元法计算不定积分
- 第四课用分部积分法计算不定积分
- 第五课计算定积分、广义积分(广义积分也叫反常积分)
- 第六课判断广义积分的敛散性(广义积分也叫反常积分)
- 第七课积分中值定理
- 第八课利用拉格朗日中值定理证明积分不等式
- 第九课利用柯西积分不等式证明积分不等式
- 第十课变限积分函数的性质
- 第十一课变限积分函数求导
- 第十二课利用变上限积分函数证明积分不等式
- 第十三课利用定积分求数列极限
- 第十四课利用定积分求平面区域面积
- 第十五课利用定积分求旋转体侧面积
- 第十六课利用定积分求旋转体体积
- 关于有理函数的不定积分的说明
第四章:常微分方程
- 第一课一阶微分方程(上)
- 第二课一阶微分方程(中)
- 第四课常系数齐次线性微分方程
- 第五课常系数非齐次线性微分方程
- 第六课线性微分方程的解的结构
- 第七课可降阶的高阶微分方程
高数下
第一章:多元函数微分学
-
极值
- 第一课一般函数求无条件极值
- 第二课利用定义判断极值点
- 第三课在约束条件下找出可能的极值点
-
连续、可导、可微
- 第一课判断函数在点(x0,y0)处是否可微
- 第二课判断函数在点(x0,y0)处是否连续
- 第三课连续、可导、可微的关系
-
偏导
- 第一课求偏导(简单情况)
- 第二课求偏导(复杂情况)
- 第三课用f′表示部分偏导
- 第四课用公式法求隐函数的偏导
- 第五课用两边同求偏导法求隐函数的偏导
- 第六课求某点的偏导值
- 第七课已知偏导数,通过积分求表达式
- 第八课变量代换下化简偏导数满足的关系式
-
全微分
- 第一课求全微分
- 第二课已知全微分,求全微分里的未知数
-
重极限
- 第一课计算重极限
- 第二课证明重极限不存在
-
最值
- 第一课在约束条件下求最值、最值点
- 第二课在区域上求最值、最值点
第二章:二重积分
- 第一课计算二次积分
- 第二课求二重积分
- 第三课交换二次积分的积分次序
- 第四课通过交换二次积分的积分次序来计算积分
- 第五课通过极坐标变换来计算积分
- 第六课通过直角坐标变换来计算积分
- 第七课通过对称性来计算积分
- 第八课通过轮换对称性来计算积分
- 第九课通过积分区域的形心来计算积分
- 第十课比较二重积分的大小
- 第十一课二重积分中值定理
- 第十二课函数表达式含二重积分
线性代数
课时1行列式的性质
课时2行列式的计算及应用
课时3矩阵的运算上(加减、相乘、取行列式)
课时4矩阵的运算下(转置、逆、秩)
课时5向量组与线性空间
课时6解方程组
课时7方阵对角化及其应用
课时8二次型

相关文章:

数二思维导图
高数上 第一章:函数、极限、连续 函数 函数的单调性、周期性、奇偶性复合函数 极限 求直接代入型的极限求∞∞型的极限用等价无穷小代换求00型的极限用洛必达法则求00型或∞∞型的极限求∞•0型的极限求幂指函数的极限函数的左右极限及需要求左右极限的情形极限的…...
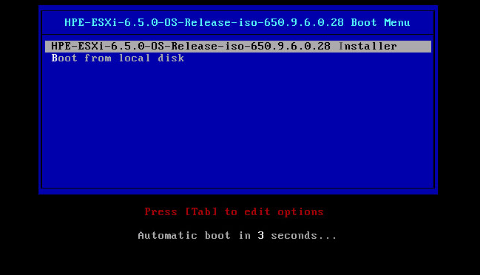
ESXI6.5安装教程
设置从IPMI Virtual Disk 3000启动,出现如下界面: 默认选择第一项,回车安装 安装程序正在检测服务器硬件信息,如果不满足系统安装条件会跳出错误提示。 检测完成之后会出现下面界面 回车 按F11 这里列出了服务器硬盘信息&#…...

2023-9-25 美团售后服务系统后端一面【2024秋招】
1 实习 1.1 讲讲你做的一个需求,为什么这么做之类的 答: 1.2 什么是接线 1.3 什么的初始接线,和权威接线 答:初始接线是现状,权威是规划中的 1.4 为什么要做比较呢? 答:运维人员需要查看…...

YOLOv5改进实战 | GSConv + SlimNeck双剑合璧,进一步提升YOLO!
前言 轻量化网络设计是一种针对移动设备等资源受限环境的深度学习模型设计方法。下面是一些常见的轻量化网络设计方法: 网络剪枝:移除神经网络中冗余的连接和参数,以达到模型压缩和加速的目的。分组卷积:将卷积操作分解为若干个较小的卷积操作,并将它们分别作用于输入的不…...

Redis之zset在异步队列上的应用
当遇到并发的客户端请求时,为了缓解服务端的处理压力,当请求对响应的处理的实时性要求不高时,可以实现一个异步的请求消息队列。 一种实现策略是使用redis的zset,将消息的到期处理时间作为score,然后用多个线程去轮训…...

day4:Node.js 核心库
day4:Node.js 核心库 文章目录 day4:Node.js 核心库常用工具模块util 模块Moment 模块Lodash 模块web模块文件模块path 模块常用工具模块 Node.js有许多常用的工具,以下是一些常见的: util: 是一个Node.js 核心模块,提供常用函数的集合,用于弥补核心 JavaScript 的功能…...

PHP非对称与对称双向加密解密的方式
目录 RSA非对称加密解密: 什么是RSA非对称加密解密解析: 解析: 为什么使用: 有什么优点: DEMO: AES、DES、3DES等对称加密解密: 解析: 为什么使用: 有什么优点: DEMO: RSA非对称加密解密: 什么是RSA非对称加密解密解析: 解析: RSA非对称加密…...

C++之struct匿名结构体实例(二百四十四)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

npm publish发布到在线仓库时,提示:Scope not found
当npm publish发布时,控制台提示:Scope not found,具体错误信息如下: npm notice npm ERR! code E404 npm ERR! 404 Not Found - PUT https://registry.npmjs.org/xxx%2fxxx - Scope not found npm ERR! 404 npm ERR! 404 xxx/xx…...

AWS Lambda 操作 RDS 示例
实现目标 创建一个 Lambda 接收调用时传入的数据, 写入 RDS 数据库 Post 表存储文章信息. 表结构如下: idtitlecontentcreate_date1我是标题我是正文内容2023-10-21 15:20:00 AWS 资源准备 RDS 控制台创建 MySQL 实例, 不允许 Public access (后面 Lambda 需要通过 VPC 访问…...
【java爬虫】使用selenium获取某交易所公司半年报数据
引言 上市公司的财报数据一般都会进行公开,我们可以在某交易所的官方网站上查看这些数据,由于数据很多,如果只是手动收集的话可能会比较耗时耗力,我们可以采用爬虫的方法进行数据的获取。 本文就介绍采用selenium框架进行公司财…...
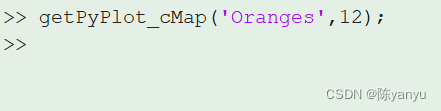
MATLAB - 不能使用PYTHON,缺少matplotlib模块的解决办法
matlab缺少python-matplotlib模块的解决办法 1. 前言、概述2. 解决办法3. 可能出现问题4. 结果 1. 前言、概述 起因是我用习惯的colormap函数getPyPlot_cMap不能用了:【这个函数要调用PYTHON】 报错的地方: ModuleNotFoundError: No module named ‘ma…...
mk语法示例
这里写自定义目录标题 欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants 创建一个自定义列表如何创建一个…...

英语什么时候加s和es
名词变复数一般情况下加s,以s,x,ch,sh结尾加es。一个名词如果表示一个或一样东西,它取单数形式,如果表示两个或更多的这类东西,则需要用名词复数形式。 1 以s,x,sh,ch结尾的词,加es。 2 以辅音字母(除a/e/…...
unity中方向的两种表示:欧拉角和四元数
欧拉角:简单来说就是你可以选择 0度~360度 的范围 四元数:在计算机图像学中,四元数用于物体的旋转,是一种复杂,但效率较高的旋转方式 Quaternion结构体代表一个四元数,包含一个标量和一个三维向量&#x…...

ViT-L-14.pt下载load checkpoint from xxx
load checkpoint from E:\BaiduNetdiskDownload\sd-webui-aki-v4\models\BLIP\model_base_caption_capfilt_large.pth stable diffusion反推提示词出现此提示时,需安装以下模型至sd-webui-aki-v4.cache\clip\目录 ViT-L-14.pt https://openaipublic.azureedge.net/…...
机械设备经营小程序商城的作用是什么
由于机械设备厂商品牌需要各地招商代理,因此在管理方面也需要工具进行高效管理。如今各个行业都在开展数字化转型解决行业所遇难题或通过线上销售解决传统三公里难题及品牌扩张难题、用户消费渠道少等难题,构建会员体系精细化管理,同时还需要…...

小程序跨页面传递参数的几种方式
当我们在开发小程序时,经常会遇到需要在不同页面之间传递数据的情况。为了实现页面间的数据传递,小程序提供了多种方法。下面将介绍几种常用的传递数据的方法。 URL参数传递:这是一种简单直接的传递数据的方式。在跳转页面时,可以…...

【算法与数据结构】--高级算法和数据结构--高级数据结构
一、堆和优先队列 堆(Heap)是一种特殊的树状数据结构,通常用于实现优先队列。堆有两种主要类型:最大堆和最小堆。最大堆是一棵树,其中每个父节点的值都大于或等于其子节点的值,而最小堆是一棵树࿰…...

小工具 - Python图片转PDF文件
前言 主要整理记载一些python实现的小脚本,网上基本转换要会员,懒得搞了,这个一键生成,可以打包成exe文件使用 单张图片转换成pdf、图片批量转换成pdf # coding UTF-8 import os from io import BytesIO from PIL import Imag…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...
