【算法与数据结构】--高级算法和数据结构--高级数据结构
一、堆和优先队列
堆(Heap)是一种特殊的树状数据结构,通常用于实现优先队列。堆有两种主要类型:最大堆和最小堆。最大堆是一棵树,其中每个父节点的值都大于或等于其子节点的值,而最小堆是一棵树,其中每个父节点的值都小于或等于其子节点的值。堆的主要特点是根节点具有最大或最小值,这使得堆非常适合处理具有优先级的数据。
优先队列(Priority Queue)是一种抽象数据类型,通常基于堆实现。它允许在插入元素时指定优先级,并在删除元素时始终返回具有最高(或最低)优先级的元素。这使得优先队列适用于需要按优先级处理元素的应用,如任务调度、图算法(如Dijkstra算法)、模拟系统等。
以下是关于堆和优先队列的关键点:
1.1 堆的特点:
- 堆是一棵树,通常是二叉树,具有最大堆和最小堆两种类型。
- 在最大堆中,根节点具有最大值,每个父节点的值大于或等于子节点的值。
- 在最小堆中,根节点具有最小值,每个父节点的值小于或等于子节点的值。
- 堆通常是一个完全二叉树,可以使用数组来表示。
- 常见的堆操作包括插入元素和删除根节点。
1.2 优先队列的特点:
- 优先队列是一个抽象数据类型,允许插入元素并根据优先级删除元素。
- 通常基于堆来实现优先队列,因为堆可以高效地维护元素的优先级。
- 优先队列的常见操作包括插入元素、删除具有最高(或最低)优先级的元素。
- 优先队列通常用于任务调度、最短路径算法、模拟系统等需要按优先级处理元素的应用。
当在C#和Java中实现堆和优先队列时,可以使用内置的数据结构和类来完成这些任务。以下是使用C#和Java的示例代码:
1.3 在C#中使用堆和优先队列:
C#中可以使用 System.Collections.Generic 命名空间提供的 SortedSet 类或 PriorityQueue 来实现堆和优先队列。
使用 SortedSet(最小堆)实现优先队列:
using System;
using System.Collections.Generic;class Program
{static void Main(){SortedSet<int> minHeap = new SortedSet<int>();minHeap.Add(3);minHeap.Add(1);minHeap.Add(4);int highestPriority = minHeap.Min;Console.WriteLine("Highest priority element: " + highestPriority);minHeap.Remove(highestPriority);}
}
1.4 在Java中使用堆和优先队列:
在Java中,你可以使用 PriorityQueue 类来实现堆和优先队列。
使用 PriorityQueue(最小堆)实现优先队列:
import java.util.PriorityQueue;public class Main {public static void main(String[] args) {PriorityQueue<Integer> minHeap = new PriorityQueue<>();minHeap.add(3);minHeap.add(1);minHeap.add(4);int highestPriority = minHeap.poll();System.out.println("Highest priority element: " + highestPriority);}
}
这两个示例分别展示了如何在C#和Java中使用内置的数据结构实现最小堆和优先队列。这些数据结构提供了高效的元素插入和删除,适用于按优先级处理元素的场景。需要注意的是,PriorityQueue 在Java中默认是最小堆,如果需要最大堆,可以通过提供自定义比较器来实现。
二、树的高级应用
树是计算机科学中一种重要的数据结构,具有许多高级应用。下面将讨论一些树的高级应用,并提供C#和Java的示例代码。
2.1 平衡二叉搜索树(Balanced Binary Search Tree)
平衡二叉搜索树是一种特殊的二叉搜索树,确保树的高度保持平衡,以便快速的查找、插入和删除操作。在C#和Java中,可以使用 SortedSet(C#)和 TreeSet(Java)实现平衡二叉搜索树。
C#示例:
using System;
using System.Collections.Generic;class Program
{static void Main(){SortedSet<int> balancedBST = new SortedSet<int>();balancedBST.Add(5);balancedBST.Add(3);balancedBST.Add(7);Console.WriteLine("In-order traversal of the balanced BST:");foreach (var item in balancedBST){Console.WriteLine(item);}}
}
Java示例:
import java.util.TreeSet;public class Main {public static void main(String[] args) {TreeSet<Integer> balancedBST = new TreeSet<>();balancedBST.add(5);balancedBST.add(3);balancedBST.add(7);System.out.println("In-order traversal of the balanced BST:");for (int item : balancedBST) {System.out.println(item);}}
}
2.2 红黑树(Red-Black Tree)
红黑树是一种自平衡的二叉搜索树,它确保在插入和删除操作后树仍然保持平衡。在C#和Java中,可以使用内置的 SortedSet(C#)和 TreeSet(Java)来实现红黑树。
2.3 堆(Heap)
堆是一种特殊的树形数据结构,常用于实现优先队列。堆可以是最小堆或最大堆,允许高效的插入和删除操作。
C#示例:
using System;
using System.Collections.Generic;class Program
{static void Main(){// 使用 SortedSet 实现最小堆SortedSet<int> minHeap = new SortedSet<int>();minHeap.Add(5);minHeap.Add(3);minHeap.Add(7);int highestPriority = minHeap.Min;Console.WriteLine("Highest priority element: " + highestPriority);}
}
Java示例:
import java.util.PriorityQueue;public class Main {public static void main(String[] args) {// 使用 PriorityQueue 实现最小堆PriorityQueue<Integer> minHeap = new PriorityQueue<>();minHeap.add(5);minHeap.add(3);minHeap.add(7);int highestPriority = minHeap.poll();System.out.println("Highest priority element: " + highestPriority);}
}
2.4 字典树(Trie)
字典树是一种树形数据结构,用于高效地存储和检索字符串数据。它通常用于搜索引擎和拼写检查等应用。
C#示例:
public class TrieNode
{public Dictionary<char, TrieNode> Children = new Dictionary<char, TrieNode>();public bool IsEndOfWord;
}public class Trie
{private TrieNode root = new TrieNode();public void Insert(string word){TrieNode node = root;foreach (char c in word){if (!node.Children.ContainsKey(c))node.Children[c] = new TrieNode();node = node.Children[c];}node.IsEndOfWord = true;}public bool Search(string word){TrieNode node = root;foreach (char c in word){if (!node.Children.ContainsKey(c))return false;node = node.Children[c];}return node.IsEndOfWord;}
}
Java示例:
class TrieNode {Map<Character, TrieNode> children = new HashMap<>();boolean isEndOfWord;
}public class Trie {private TrieNode root = new TrieNode();public void insert(String word) {TrieNode node = root;for (char c : word.toCharArray()) {node.children.putIfAbsent(c, new TrieNode());node = node.children.get(c);}node.isEndOfWord = true;}public boolean search(String word) {TrieNode node = root;for (char c : word.toCharArray()) {if (!node.children.containsKey(c))return false;node = node.children.get(c);}return node.isEndOfWord;}
}
这些示例展示了在C#和Java中实现平衡二叉搜索树、红黑树、堆和字典树的方法。这些高级应用树结构在各种领域中发挥着关键作用,包括数据库索引、搜索引擎、数据结构、字符串处理等。
四、高级图算法
高级图算法是计算机科学中的重要领域,用于解决各种复杂问题,如最短路径、最小生成树、网络流、最大流最小割等。以下是一些高级图算法的介绍,并提供C#和Java的示例代码。
4.1 最短路径算法
最短路径算法用于找到两个节点之间的最短路径,通常用于导航、路线规划和网络分析。其中最著名的算法之一是Dijkstra算法。
C#示例:
using System;
using System.Collections.Generic;class Dijkstra
{public void FindShortestPath(Dictionary<int, Dictionary<int, int>> graph, int start){// Implementation of Dijkstra's algorithm}static void Main(){Dictionary<int, Dictionary<int, int>> graph = new Dictionary<int, Dictionary<int, int>>{{ 1, new Dictionary<int, int> { { 2, 5 }, { 3, 3 } } },{ 2, new Dictionary<int, int> { { 3, 2 }, { 4, 6 } } },{ 3, new Dictionary<int, int> { { 4, 7 } } },{ 4, new Dictionary<int, int> { } }};Dijkstra dijkstra = new Dijkstra();dijkstra.FindShortestPath(graph, 1);}
}
Java示例:
import java.util.*;
import java.util.stream.Collectors;public class Dijkstra {public void findShortestPath(Map<Integer, Map<Integer, Integer>> graph, int start) {// Implementation of Dijkstra's algorithm}public static void main(String[] args) {Map<Integer, Map<Integer, Integer>> graph = new HashMap<>();graph.put(1, new HashMap<>() {{ put(2, 5); put(3, 3); }});graph.put(2, new HashMap<>() {{ put(3, 2); put(4, 6); }});graph.put(3, new HashMap<>() {{ put(4, 7); }});graph.put(4, new HashMap<>());Dijkstra dijkstra = new Dijkstra();dijkstra.findShortestPath(graph, 1);}
}
4.2 最小生成树算法
最小生成树算法用于找到一个连通图中生成树,其中边的权重总和最小。其中最著名的算法之一是Prim算法。
C#示例:
using System;
using System.Collections.Generic;class Prim
{public List<Tuple<int, int, int>> FindMinimumSpanningTree(List<Tuple<int, int, int>> edges, int vertexCount){// Implementation of Prim's algorithm}static void Main(){List<Tuple<int, int, int>> edges = new List<Tuple<int, int, int>>{Tuple.Create(1, 2, 5),Tuple.Create(1, 3, 3),Tuple.Create(2, 3, 2),Tuple.Create(2, 4, 6),Tuple.Create(3, 4, 7)};int vertexCount = 4;Prim prim = new Prim();var minimumSpanningTree = prim.FindMinimumSpanningTree(edges, vertexCount);}
}
Java示例:
import java.util.*;public class Prim {public List<Edge> findMinimumSpanningTree(List<Edge> edges, int vertexCount) {// Implementation of Prim's algorithm}public static void main(String[] args) {List<Edge> edges = Arrays.asList(new Edge(1, 2, 5),new Edge(1, 3, 3),new Edge(2, 3, 2),new Edge(2, 4, 6),new Edge(3, 4, 7));int vertexCount = 4;Prim prim = new Prim();List<Edge> minimumSpanningTree = prim.findMinimumSpanningTree(edges, vertexCount);}
}class Edge {int source, destination, weight;Edge(int source, int destination, int weight) {this.source = source;this.destination = destination;this.weight = weight;}
}
这些示例涵盖了最短路径算法和最小生成树算法的基本实现。根据具体需求和图的表示,你可以使用不同的数据结构和算法来解决高级图问题。这些算法在各种应用中都非常有用,包括网络规划、运输优化、社交网络分析等。
五、总结
堆和优先队列是处理具有优先级的数据的重要工具。堆分为最大堆和最小堆,用于快速查找最大或最小元素。优先队列是基于堆的数据结构,用于按优先级处理元素。堆和优先队列可以在C#和Java中使用内置的数据结构实现。树的高级应用包括平衡二叉搜索树、红黑树、堆、字典树等,这些树结构在数据库索引、搜索引擎、字符串处理等领域发挥着关键作用。高级图算法涵盖最短路径和最小生成树算法,如Dijkstra算法和Prim算法,用于网络规划、运输优化和社交网络分析等应用。
相关文章:

【算法与数据结构】--高级算法和数据结构--高级数据结构
一、堆和优先队列 堆(Heap)是一种特殊的树状数据结构,通常用于实现优先队列。堆有两种主要类型:最大堆和最小堆。最大堆是一棵树,其中每个父节点的值都大于或等于其子节点的值,而最小堆是一棵树࿰…...

小工具 - Python图片转PDF文件
前言 主要整理记载一些python实现的小脚本,网上基本转换要会员,懒得搞了,这个一键生成,可以打包成exe文件使用 单张图片转换成pdf、图片批量转换成pdf # coding UTF-8 import os from io import BytesIO from PIL import Imag…...
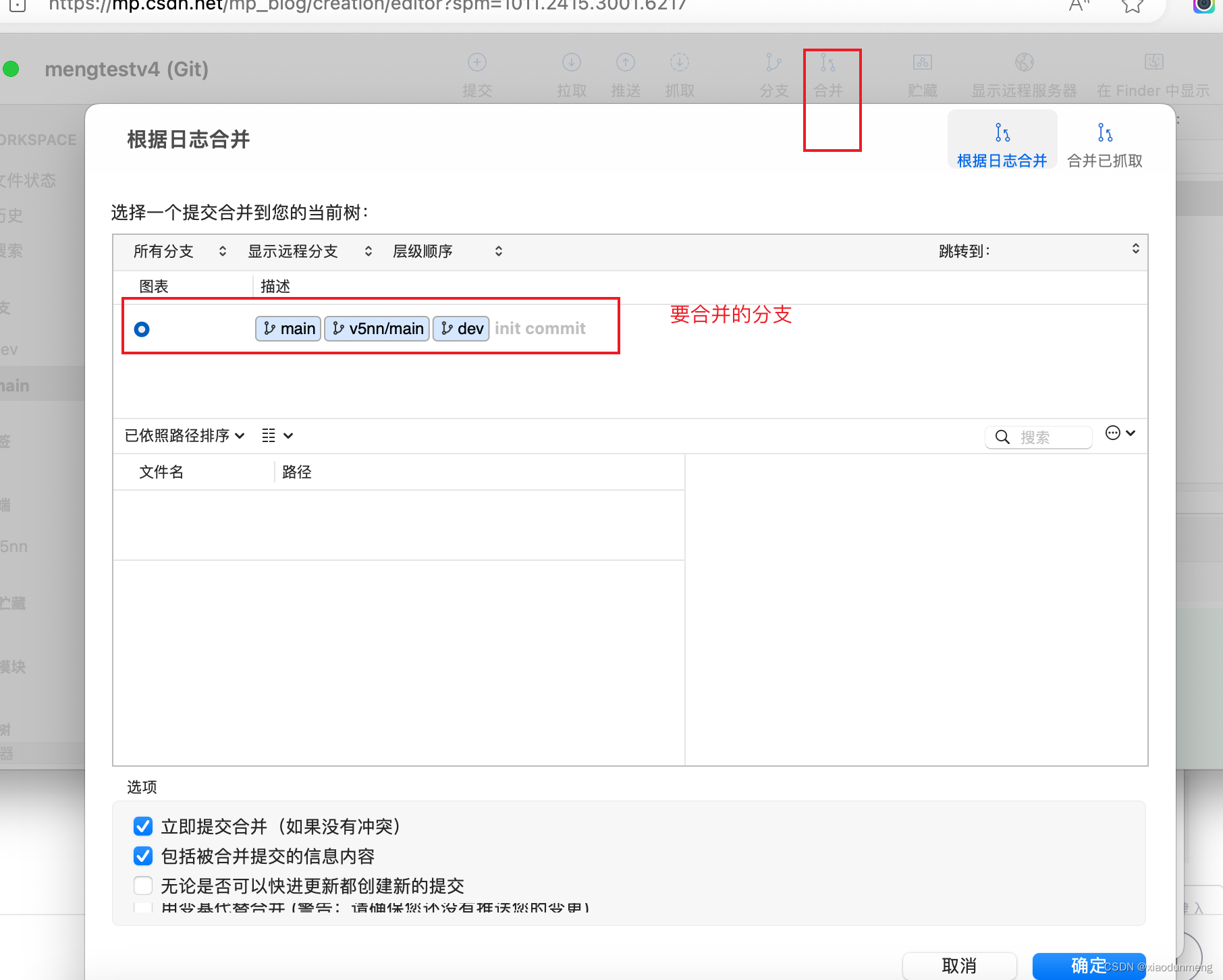
bitbucket.org 用法
这个网站需要魔法,注册完成后添加厂库时间2023.10 图1 图2 第二张图 ,不要.gitignore文件 sourcetree 1,创建前端项目 npm create vitelatest 2.打开vscode创建本地Git 看到Git代提交的文件 sourcetree,新建 已存在的本地厂库 提交到Git 添…...

lodash常用方法合集
安装lodash 建议安装lodash-es,lodash-es 是 lodash 的 es modules 版本 ,是着具备 ES6 模块化的版本,体积小。按需引入。 示例 npm i lodash-es import { chunk,compact } from lodash-es; /**按需引入*/ 1.chunk 数组分组 chunk(arra…...

Nginx平滑升级重定向rewrite
文章目录 Nginx平滑升级&重定向rewritenginx平滑升级流程环境查看旧版的配置信息下载新版nginx源码包和功能模块包编译配置新版本平滑升级验证 重定向rewrite配置重定向准发访问测试 Nginx平滑升级&重定向rewrite nginx平滑升级 流程 平滑升级: (升级版本、增加新功…...

Mysql基础与高级汇总
SQL语言分类 DDL:定义 DML:操作 DCL:控制(用于定义访问权限和安全级别) DQL:查询 Sql方言 ->sql:结构化查询语言 mysql:limit oracle:rownum sqlserver:top 但是存储过程:每一种数据库软件一样SQL语法要求: SQL语句可以单行或多行书写&…...

为什么避免在循环、条件或嵌套函数中调用 Hooks
为什么避免在循环、条件或嵌套函数中调用 Hooks 为了确保 Hook 在每一次渲染中都按照同样的顺序被调用。这让 React 能够在多次的 useState 和 useEffect 调用之间保持 hook 状态的正确。 我们可以在单个组件中使用多个 State Hook 或 Effect Hook: function Form…...

自然语言处理---Transformer机制详解之BERT模型特点
1 BERT的优点和缺点 1.1 BERT的优点 通过预训练, 加上Fine-tunning, 在11项NLP任务上取得最优结果.BERT的根基源于Transformer, 相比传统RNN更加高效, 可以并行化处理同时能捕捉长距离的语义和结构依赖.BERT采用了Transformer架构中的Encoder模块, 不仅仅获得了真正意义上的b…...

c语言基础:L1-048 矩阵A乘以B
给定两个矩阵A和B,要求你计算它们的乘积矩阵AB。需要注意的是,只有规模匹配的矩阵才可以相乘即若A有Ra行、Ca列,B有Rb行、Cb列,则只有Ca与Rb相等时,两个矩阵才能相乘。 输入格式: 输入先后给出…...
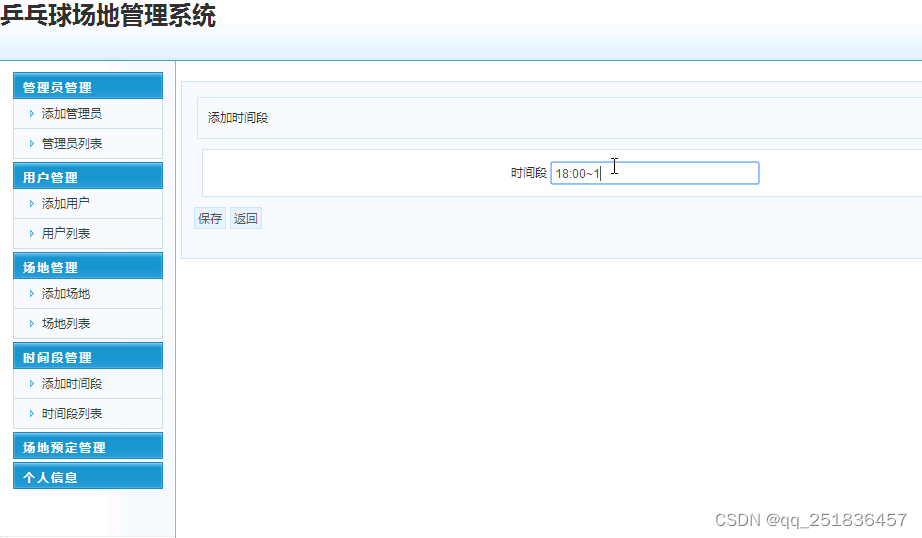
asp.net乒乓球场地管理系统VS开发sqlserver数据库web结构c#编程Microsoft Visual Studio
一、源码特点 asp.net乒乓球场地管理系统是一套完善的web设计管理系统,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为vs2010,数据库为sqlserver2008,使用c#语 言开发 asp.net 乒乓球场地管理系统 二…...

git仓库中增加子仓库
在 Git 中包含另一个 Git 仓库通常使用 Git 子模块(Git Submodule)来实现。子模块允许你在一个 Git 仓库中包含另一个 Git 仓库,从而在一个仓库中管理多个相关但独立的项目。 以下是如何将一个 Git 仓库包含为另一个 Git 仓库的子模块的步骤…...
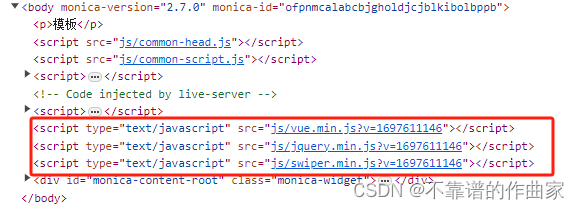
html中公用css、js提取、使用
前言 开发中,页面会有引用相同的css、js的情况,如需更改则每个页面都需要调整,重复性工作较多,另外在更改内容之后上传至服务器中会有缓存问题,特针对该情况对公用css、js进行了提取并对引用时增加了版本号 一、提取…...

Jprofiler V14中文使用文档
JProfiler介绍 什么是JProfiler? JProfiler是一个用于分析运行JVM内部情况的专业工具。 在开发中你可以使用它,用于质量保证,也可以解决你的生产系统遇到的问题。 JProfiler处理四个主要问题: 方法调用 这通常被称为"CPU分析"。方法调用可以通过不同的方式进行测…...
基于PHP的蛋糕甜品商店管理系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding) 代码参考数据库参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者&am…...
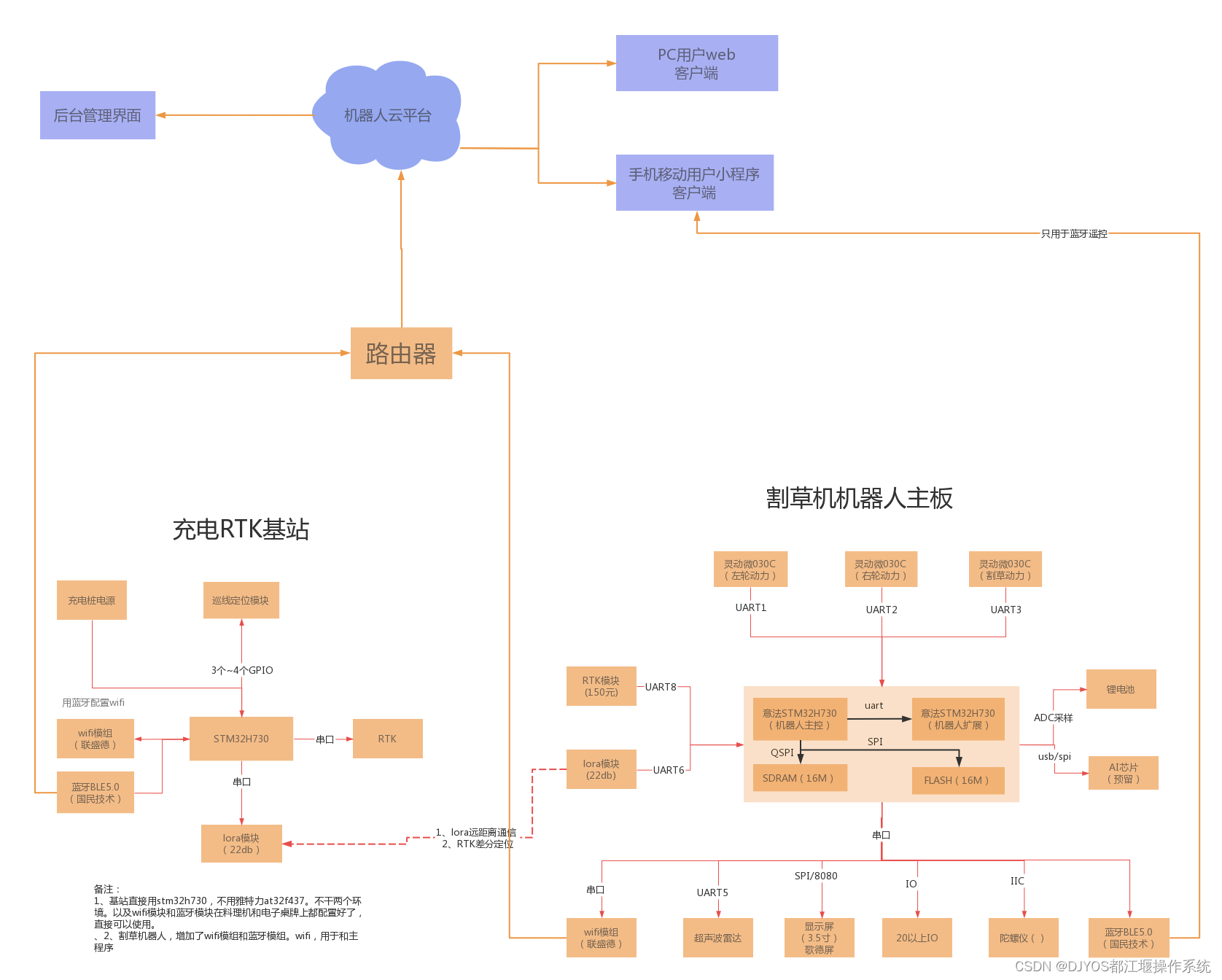
DJYROS产品:基于DJYOS的国产自主割草机器人解决方案
基于都江堰泛计算操作系统的国产自主机器人操作系统即将发布…… 1、都江堰机器人操作系统命名:DJYROS 2、机器人算法:联合行业自主机器人厂家,构建机器人算法库。 3、机器人芯片:联合行业机器人AI芯片公司,构建专用…...

A预测蛋白质结构
基于AlphaFold2进行蛋白质结构预测的文章解析 RoseTTAFold: Tunyasuvunakool, K., Adler, J., Wu, Z. et al. Highly accurate protein structure prediction for the human proteome. Nature 596, 590–596 (2021) AlphaFold2: Accurate prediction of protein structures a…...

rust学习~slice迭代器
背景 pub fn iter(&self) -> Iter<_, T>查看Iter 结构体 pub struct Iter<a, T> whereT: a, {/* private fields */ }对迭代器求和 sum fn sum<S>(self) -> S whereSelf: Sized, // 该函数只能在具有已知大小的类型上调用S: Sum<Self::Item…...
python免杀初探
文章目录 loader基础知识loader参数介绍 evilhiding项目地址免杀方式修改加载器花指令混淆loader源码修改签名加壳远程条件触发修改ico的md5加密 loader基础知识 loader import ctypes #(kali生成payload存放位置) shellcode bytearray(b"shellc…...
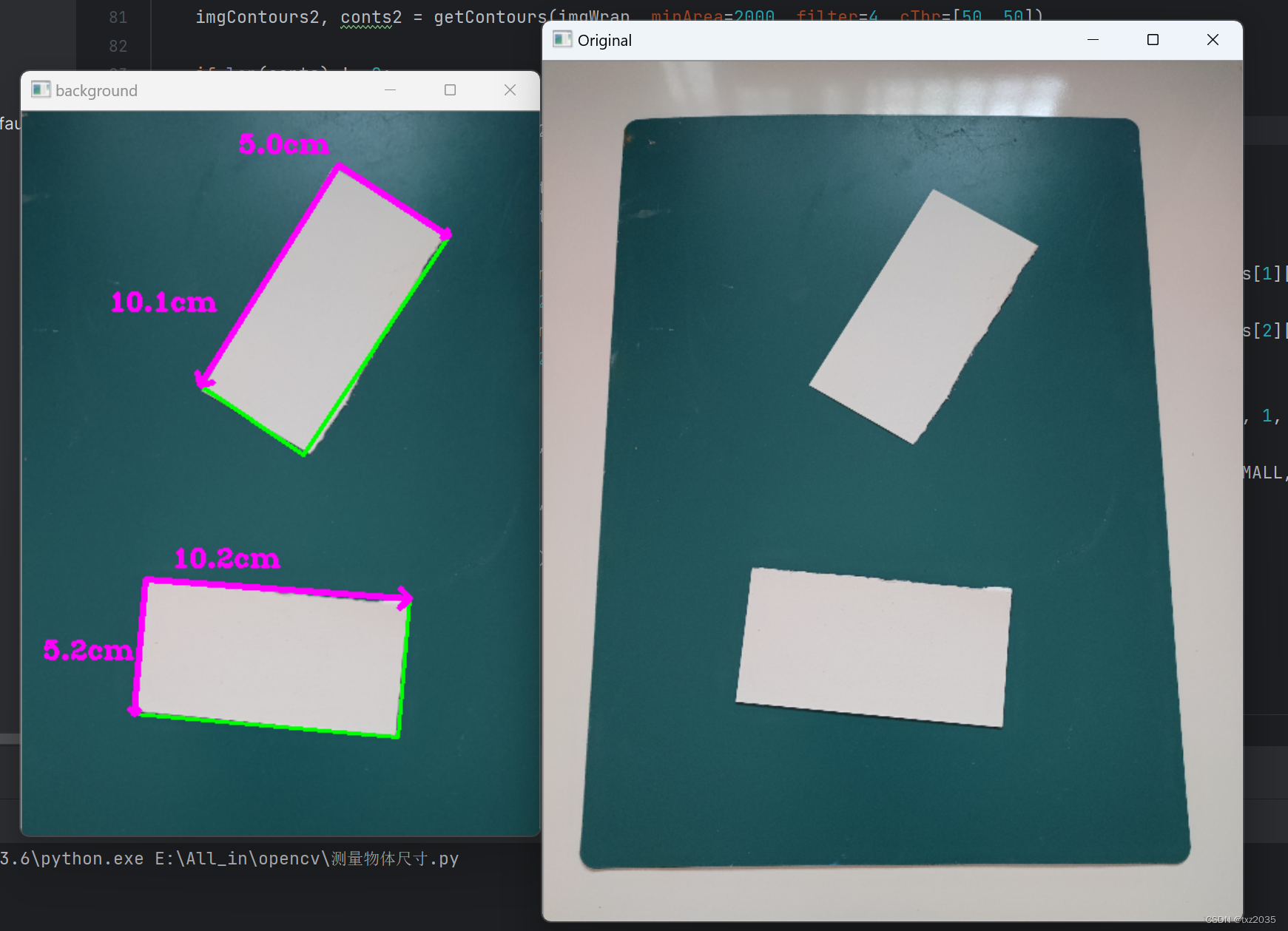
OpenCV实现物体尺寸的测量
一 ,项目分析 物体尺寸测量的思路是找一个确定尺寸的物体作为参照物,根据已知的计算未知物体尺寸。 如下图所示,绿色的板子尺寸为220*300(单位:毫米),通过程序计算白色纸片的长度。 主要是通过…...

投资研报的优质网站
投资研报:https://www.zhihu.com/question/357713923/answer/2304672553...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
