PHP非对称与对称双向加密解密的方式
目录
RSA非对称加密解密:
什么是RSA非对称加密解密解析:
解析:
为什么使用:
有什么优点:
DEMO:
AES、DES、3DES等对称加密解密:
解析:
为什么使用:
有什么优点:
DEMO:
RSA非对称加密解密:
什么是RSA非对称加密解密解析:
解析:
RSA非对称加密解密算法是一种广泛应用于信息安全领域的加密算法。它不同于常规的对称加密,如相同的密钥用于加密和解密,而是使用一对不同的密钥,即公钥和私钥,进行加密和解密的过程。
在RSA加密算法中,甲方首先生成一对密钥,并将其中的一个作为公钥公开给其他方;得到公钥的乙方则使用该公钥对机密信息进行加密后发送给甲方;最后,甲方用自己的另一个专用密钥,即私钥,对接收到的加密信息进行解密。
值得一提的是,RSA加密算法的加密原理基于一个非常简单但有深远影响的数论事实:两个大质数相乘易事,但一个大数分解为两个质数的乘积却困难重重。这就使得RSA算法具有极高的安全性,极其难以被破解。
然而,虽然RSA算法的安全性极高,但其实施过程中可能会面临一些问题,例如密钥配送问题。这是因为在确定下来的密钥如何让双方都知道的过程中,密钥本身也是信息,其传输过程也可能被拦截和窃取。因此,解决密钥配送问题对于确保RSA算法的安全性至关重要。
为什么使用:
RSA非对称加密解密算法在信息安全领域得到广泛应用,其最主要的优点在于安全性极高。与常规的对称加密不同,如相同的密钥用于加密和解密,RSA算法使用的是一对不同的密钥,即公钥和私钥,进行加密和解密的过程。公钥是公开的,私钥是自己保存的,无需将私钥给别人。
然而,RSA算法也存在一些缺点。首要的一点就是加密和解密花费时间长、速度慢,只适合对少量数据进行加密。此外,RSA算法的加密长度为2048位,因此对于服务端的消耗是比较大的,所以计算的速度也会比较慢,效率相对较低。
总的来说,虽然RSA算法的安全性和兼容性都很强,但是由于其加密解密效率较低,所以在实际应用中通常结合其他加密方法一起使用,例如:针对C/S模型,服务端计算出一对秘钥pub/pri。将私钥保密,将公钥公开。客户端请求服务端时,拿到服务端的公钥pub。客户端通过AES计算出一个对称加密的秘钥X。然后使用pub将X进行加密。客户端将加密后的密文发送给服务端。
有什么优点:
1.RSA非对称加密解密算法的优点主要体现在其高度的安全性上。首先,该算法的运作原理基于一个深奥的数论事实:将两个大素数相乘很容易,但反之却极其困难。因此,只要这两个素数的秘密被妥善保管,用它们加密的信息就能得到有效保护。
2.RSA算法的一个显著特点是它使用两把不同的密钥,公钥和私钥。公钥可以公开,而私钥则需要保密保存,无需将其提供给他人。这一特性使得RSA在许多场合变得非常有用,特别是在需要通过网络传输密钥的情况下。由于不需要在网络中传输密钥,因此可以避免密钥在传输过程中被窃取或篡改的风险。
3.尽管RSA算法具有很高的安全性,但它也存在一些缺点。比如,RSA算法的加解密过程可能会花费较长的时间,因此它更适合对少量数据进行加密。此外,RSA算法的效率相对较低,因此在处理大量数据时可能不太适用。为了解决这个问题,实际应用中常常会结合其他加密方式,如AES等进行混合使用。例如在C/S模型中,服务端计算出一对秘钥pub/pri,将私钥保密,将公钥公开。客户端请求服务端时,拿到服务端的公钥pub,通过AES计算出一个对称加密的秘钥X,然后使用pub将X进行加密,最后将加密后的密文发送给服务端。
DEMO:
<?php
// 生成密钥对
$keyPair = openssl_pkey_new(array("private_key_bits" => 2048,"private_key_type" => OPENSSL_KEYTYPE_RSA,
));// 获取私钥和公钥
openssl_pkey_export($keyPair, $privateKey);
$publicKey = openssl_pkey_get_details($keyPair)["key"];// 要加密的数据
$data = "Hello, World!";// 使用公钥进行加密
$encryptedData = '';
openssl_public_encrypt($data, $encryptedData, $publicKey, OPENSSL_PKCS1_OAEP_PADDING);
echo "Encrypted data: " . base64_encode($encryptedData) . PHP_EOL;// 使用私钥进行解密
$decryptedData = '';
openssl_private_decrypt($encryptedData, $decryptedData, $privateKey, OPENSSL_PKCS1_OAEP_PADDING);
echo "Decrypted data: " . $decryptedData . PHP_EOL;
?>
在这个示例中,我们首先生成了一个RSA密钥对,然后使用公钥对数据进行了加密,最后使用私钥对数据进行了解密。注意,由于RSA算法的特性,加密和解密的过程可能会花费一些时间。
AES、DES、3DES等对称加密解密:
解析:
AES、DES、3DES都是对称加密算法,也就是说加密和解密使用的是同一个密钥。
DES(Data Encryption Standard)是一种使用密钥进行加密的块算法,出自IBM的研究,后来被美国政府正式采用并开始广泛流传。然而,现在普遍认为DES由于其56位密钥长度较短,安全性不足,已经可以在短时间内被破解,因此现在使用越来越少。
3DES(Triple DES),也称TDES,是DES的加强版本,为了解决DES安全性不足的问题而出现。它使用3条56位的密钥对数据进行三次加密,使得即使攻击者拥有大量的计算资源,也难以破解。
AES(Advanced Encryption Standard)则是目前最流行的对称加密算法之一,它的密钥长度比DES更长,因此更安全。AES算法的出现正是为了取代DES。
在对称加密中,发信方将明文和加密密钥一起经过特殊加密算法处理后,使其变成复杂的加密密文发送出去。收信方收到密文后,若想解读原文,则需要使用加密用过的密钥及相同算法的逆算法对密文进行解密,才能使其恢复成可读明文。
为什么使用:
对称加密算法,如AES、DES和3DES等,被广泛使用是因为它们提供了一种高效且可靠的方法来保护数据的机密性。这些算法通过使用相同的密钥进行加密和解密操作,使得加解密过程变得相对简单快速。
然而,这些算法的安全性各不相同。例如,DES是一种早期的对称加密算法,其密钥长度为56位,虽然加密速度较快,但由于其安全性较低,易受到暴力破解和差分攻击等攻击手段的攻击,因此现在使用越来越少。 为了提高安全性,出现了3DES,也称Triple DES,这是DES向AES过渡的加密算法,它使用3条56位的密钥对数据进行三次加密,从而大大提高了加密的强度。
再进一步,AES(高级加密标准)是目前最流行的对称加密算法之一,它的密钥长度为128位或256位,安全性比DES和3DES更高。 AES算法的出现正是为了取代安全性较低的DES。 因此,在需要高度安全的场合,通常会选择使用AES等高安全性的对称加密算法来保护数据的机密性。
有什么优点:
加密速度快:相对于非对称加密算法,对称加密算法由于只需要一个密钥进行加解密操作,所以其加密速度通常更快,适合加密大文件。
安全性较高:虽然早期的DES算法由于密钥长度较短,易受到暴力破解和差分攻击等攻击手段的攻击,但是通过将其发展为3DES(Triple DES),也就是使用3条56位的密钥对数据进行三次加密,安全性得到了极大的提高。而目前最流行的AES(高级加密标准)的密钥长度为128位或256位,安全性更高。
可逆性:对称加密算法的另一个特点是密文可逆,即可以通过同一个密钥进行解密操作,从而获取原始明文。
DEMO:
<?php
// 定义密钥和明文
$key = '0123456789abcdef'; // 密钥长度为16字节(128位)
$plaintext = 'Hello, world!'; // 明文// 创建加密器对象,并指定加密模式为ECB模式
$cipher = "aes-128-ecb";
$ivlen = openssl_cipher_iv_length($cipher);
$iv = openssl_random_pseudo_bytes($ivlen);
$ciphertext = openssl_encrypt($plaintext, $cipher, $key, OPENSSL_RAW_DATA, $iv);
echo "密文:".bin2hex($ciphertext)."\n";// 创建解密器对象,并指定加密模式为ECB模式
$decipher = "aes-128-ecb";
$decrypted_text = openssl_decrypt($ciphertext, $decipher, $key, OPENSSL_RAW_DATA, $iv);
echo "解密后的明文:".$decrypted_text."\n";
?>
在这个示例中,我们首先定义了一个密钥和一个明文,然后使用AES算法对其进行了加密和解密操作.
相关文章:

PHP非对称与对称双向加密解密的方式
目录 RSA非对称加密解密: 什么是RSA非对称加密解密解析: 解析: 为什么使用: 有什么优点: DEMO: AES、DES、3DES等对称加密解密: 解析: 为什么使用: 有什么优点: DEMO: RSA非对称加密解密: 什么是RSA非对称加密解密解析: 解析: RSA非对称加密…...

C++之struct匿名结构体实例(二百四十四)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

npm publish发布到在线仓库时,提示:Scope not found
当npm publish发布时,控制台提示:Scope not found,具体错误信息如下: npm notice npm ERR! code E404 npm ERR! 404 Not Found - PUT https://registry.npmjs.org/xxx%2fxxx - Scope not found npm ERR! 404 npm ERR! 404 xxx/xx…...

AWS Lambda 操作 RDS 示例
实现目标 创建一个 Lambda 接收调用时传入的数据, 写入 RDS 数据库 Post 表存储文章信息. 表结构如下: idtitlecontentcreate_date1我是标题我是正文内容2023-10-21 15:20:00 AWS 资源准备 RDS 控制台创建 MySQL 实例, 不允许 Public access (后面 Lambda 需要通过 VPC 访问…...
【java爬虫】使用selenium获取某交易所公司半年报数据
引言 上市公司的财报数据一般都会进行公开,我们可以在某交易所的官方网站上查看这些数据,由于数据很多,如果只是手动收集的话可能会比较耗时耗力,我们可以采用爬虫的方法进行数据的获取。 本文就介绍采用selenium框架进行公司财…...
MATLAB - 不能使用PYTHON,缺少matplotlib模块的解决办法
matlab缺少python-matplotlib模块的解决办法 1. 前言、概述2. 解决办法3. 可能出现问题4. 结果 1. 前言、概述 起因是我用习惯的colormap函数getPyPlot_cMap不能用了:【这个函数要调用PYTHON】 报错的地方: ModuleNotFoundError: No module named ‘ma…...
mk语法示例
这里写自定义目录标题 欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants 创建一个自定义列表如何创建一个…...

英语什么时候加s和es
名词变复数一般情况下加s,以s,x,ch,sh结尾加es。一个名词如果表示一个或一样东西,它取单数形式,如果表示两个或更多的这类东西,则需要用名词复数形式。 1 以s,x,sh,ch结尾的词,加es。 2 以辅音字母(除a/e/…...
unity中方向的两种表示:欧拉角和四元数
欧拉角:简单来说就是你可以选择 0度~360度 的范围 四元数:在计算机图像学中,四元数用于物体的旋转,是一种复杂,但效率较高的旋转方式 Quaternion结构体代表一个四元数,包含一个标量和一个三维向量&#x…...

ViT-L-14.pt下载load checkpoint from xxx
load checkpoint from E:\BaiduNetdiskDownload\sd-webui-aki-v4\models\BLIP\model_base_caption_capfilt_large.pth stable diffusion反推提示词出现此提示时,需安装以下模型至sd-webui-aki-v4.cache\clip\目录 ViT-L-14.pt https://openaipublic.azureedge.net/…...
机械设备经营小程序商城的作用是什么
由于机械设备厂商品牌需要各地招商代理,因此在管理方面也需要工具进行高效管理。如今各个行业都在开展数字化转型解决行业所遇难题或通过线上销售解决传统三公里难题及品牌扩张难题、用户消费渠道少等难题,构建会员体系精细化管理,同时还需要…...

小程序跨页面传递参数的几种方式
当我们在开发小程序时,经常会遇到需要在不同页面之间传递数据的情况。为了实现页面间的数据传递,小程序提供了多种方法。下面将介绍几种常用的传递数据的方法。 URL参数传递:这是一种简单直接的传递数据的方式。在跳转页面时,可以…...

【算法与数据结构】--高级算法和数据结构--高级数据结构
一、堆和优先队列 堆(Heap)是一种特殊的树状数据结构,通常用于实现优先队列。堆有两种主要类型:最大堆和最小堆。最大堆是一棵树,其中每个父节点的值都大于或等于其子节点的值,而最小堆是一棵树࿰…...

小工具 - Python图片转PDF文件
前言 主要整理记载一些python实现的小脚本,网上基本转换要会员,懒得搞了,这个一键生成,可以打包成exe文件使用 单张图片转换成pdf、图片批量转换成pdf # coding UTF-8 import os from io import BytesIO from PIL import Imag…...
bitbucket.org 用法
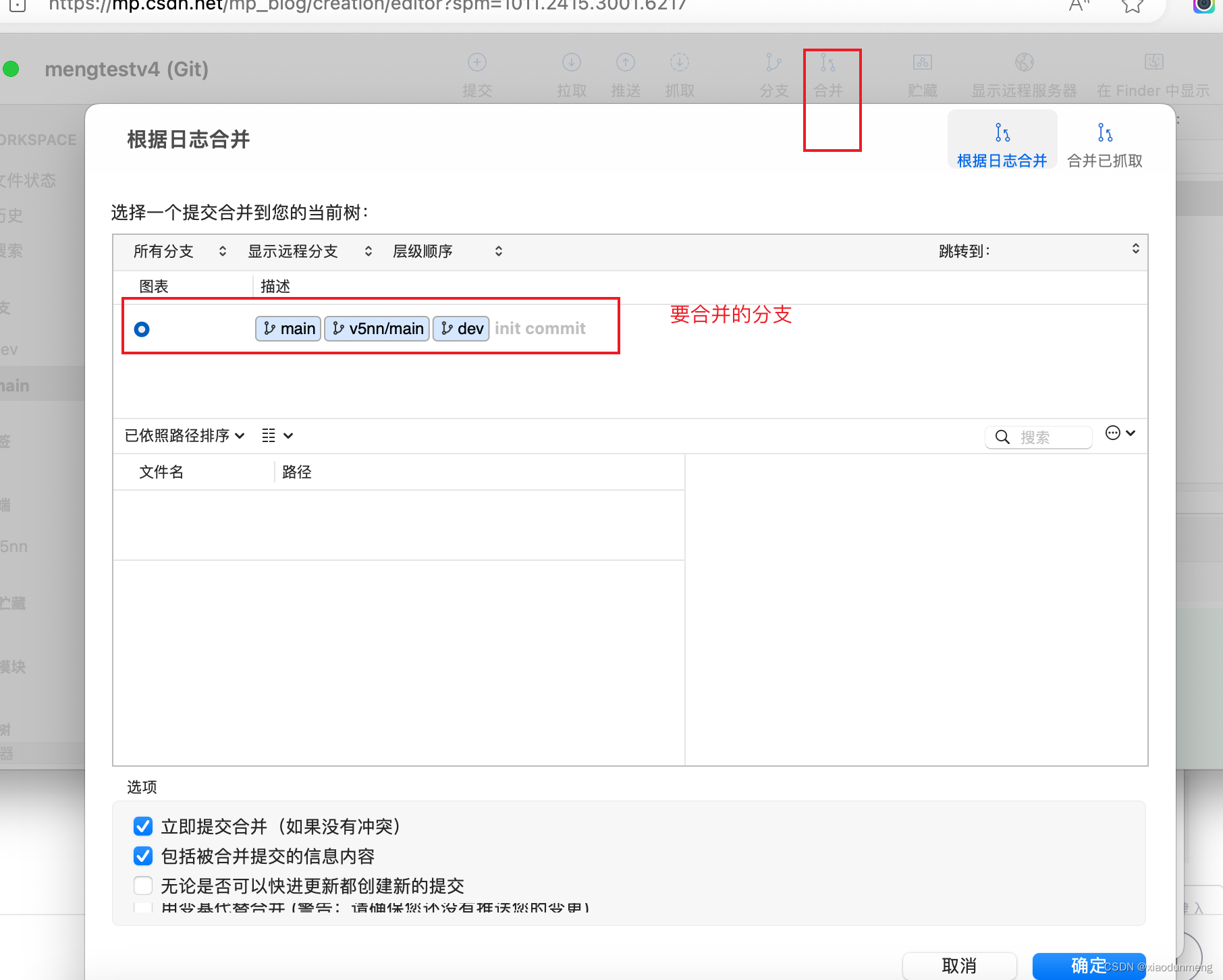
这个网站需要魔法,注册完成后添加厂库时间2023.10 图1 图2 第二张图 ,不要.gitignore文件 sourcetree 1,创建前端项目 npm create vitelatest 2.打开vscode创建本地Git 看到Git代提交的文件 sourcetree,新建 已存在的本地厂库 提交到Git 添…...

lodash常用方法合集
安装lodash 建议安装lodash-es,lodash-es 是 lodash 的 es modules 版本 ,是着具备 ES6 模块化的版本,体积小。按需引入。 示例 npm i lodash-es import { chunk,compact } from lodash-es; /**按需引入*/ 1.chunk 数组分组 chunk(arra…...

Nginx平滑升级重定向rewrite
文章目录 Nginx平滑升级&重定向rewritenginx平滑升级流程环境查看旧版的配置信息下载新版nginx源码包和功能模块包编译配置新版本平滑升级验证 重定向rewrite配置重定向准发访问测试 Nginx平滑升级&重定向rewrite nginx平滑升级 流程 平滑升级: (升级版本、增加新功…...

Mysql基础与高级汇总
SQL语言分类 DDL:定义 DML:操作 DCL:控制(用于定义访问权限和安全级别) DQL:查询 Sql方言 ->sql:结构化查询语言 mysql:limit oracle:rownum sqlserver:top 但是存储过程:每一种数据库软件一样SQL语法要求: SQL语句可以单行或多行书写&…...

为什么避免在循环、条件或嵌套函数中调用 Hooks
为什么避免在循环、条件或嵌套函数中调用 Hooks 为了确保 Hook 在每一次渲染中都按照同样的顺序被调用。这让 React 能够在多次的 useState 和 useEffect 调用之间保持 hook 状态的正确。 我们可以在单个组件中使用多个 State Hook 或 Effect Hook: function Form…...

自然语言处理---Transformer机制详解之BERT模型特点
1 BERT的优点和缺点 1.1 BERT的优点 通过预训练, 加上Fine-tunning, 在11项NLP任务上取得最优结果.BERT的根基源于Transformer, 相比传统RNN更加高效, 可以并行化处理同时能捕捉长距离的语义和结构依赖.BERT采用了Transformer架构中的Encoder模块, 不仅仅获得了真正意义上的b…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
