超详细 | 差分进化算法原理及其实现(Matlab/Python)
差分进化(Differential Evolution,DE)算法是由美国学者Storn和 Price在1995年为求解Chebyshev多项式拟合问题而提出的。算法主要通过基于差分形式的变异操作和基于概率选择的交叉操作进行优化搜索,虽然其操作名称和遗传算法相同,但实现方法有本质区别。
差分进化算法的原理简单,参数设置较少,易于编程实现,目前已被证明为是一种高效的智能优化算法,已在人工神经网络、电力、机器人、信号处理等领域得到了应用。
本文将介绍其理论模型和代码实现。
00 目录
1 差分进化算法原理
2 代码目录
3 算法性能
4 源码获取
01 差分进化算法原理
差分进化算法的基本思想源于遗传算法。
变异:DE算法是通过把种群中两个个体之间的加权差向量加到第三个个体上来产生新参数向量;
交叉:将变异向量的参数与另外预先决定的目标向量的参数按照一定的规则混合起来产生子个体;
选择:新产生的子个体只有当它比种群中的目标个体优良时才对其进行替换;
DE算法的选择操作是在完成变异、交叉之后由父代个体与新产生的候选个体――对应地进行竞争,优胜劣汰,使得子代个体总是等于或优于父代个体。
而且,DE算法给予父代所有个体以平等的机会进入下一代,不歧视劣质个体。
差分进化算法把一定比例的多个个体的差分信息作为个体的扰动量,使得算法在跳跃距离和搜索方向上具有自适应性。在进化的早期,因为种群中个体的差异性较大,使得扰动量较大,从而使得算法能够在较大范围内搜索,具有较强的勘探能力﹔到了进化的后期﹐当算法趋向于收敛时,种群中个体的差异性较小,算法在个体附近搜索,这使得算法具有较强的局部开采能力。
正是由于差分进化算法具有向种群个体学习的能力,使得其拥有其他进化算法无法比拟的性能。其具体操作如下:
(1)变异
当种群进化至第 G 代时,对父代个体Xi,G 实施变异操作得到变异个体,即:
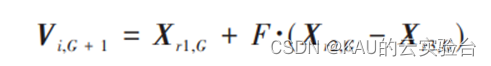
式中下标 r1,r2,r3 是在 1 和 NP(种群规模) 之间随机选择的与i不同的互异整数,Xr1,G称为基向量,( Xr2,G - Xr3,G ) 称为差分向量,F为缩放因子。如果变异个体中的参数超出边界,则该参数的值将被边界值替换。
(2)交叉
通过交叉操作产生试验个体为:
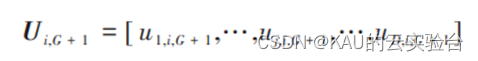
其中,
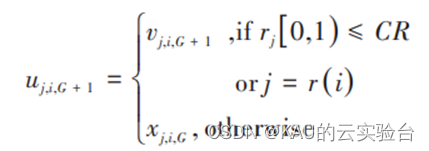
式中 rj[ 0,1) 代表第 j 次计算的随机数,CR 为交叉率。r(i)是在1和D之间随机选取的 整数,可使Ui,G + 1从Vi,G + 1获得至少一个变量。
(3)选择
对于最小化问题,在试验个体Ui,G + 1与父代个体Xi,G中选择目标函数较小的个体进入下一代种群,即:
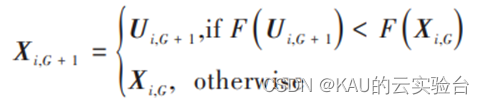
式中 F (X)代表目标函数。
算法中主要的控制参数为种群规模NP、缩放因子F、交叉率CR,通常这些参数在进化时都保持不变。
算法流程图如下:
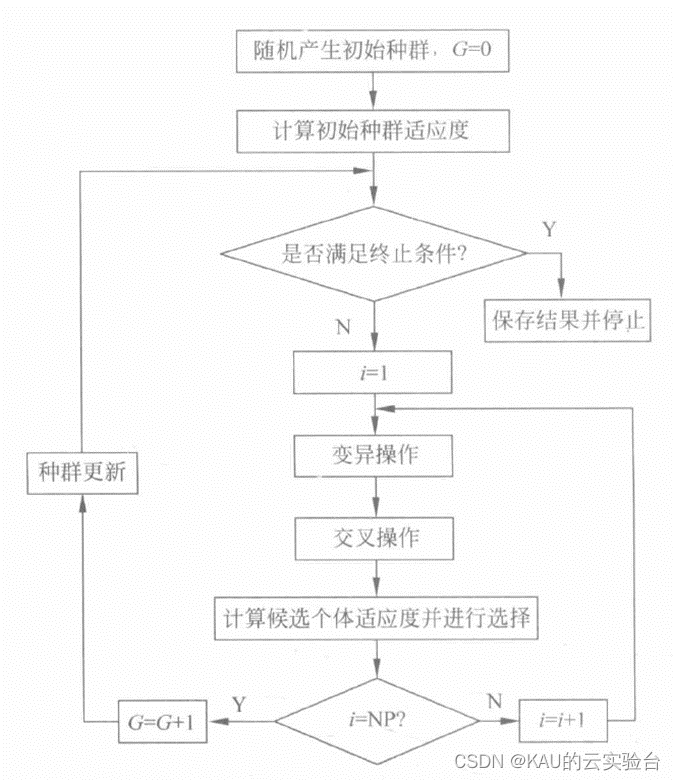
02 代码目录

MATLAB

Python

包含MATLAB 和Python的程序,考虑到很多同学获取代码后有乱码(matlab版本问题),可以将matlab版本改为2020-2022,或使用乱码解决文件夹中的txt文件即可。
部分代码:
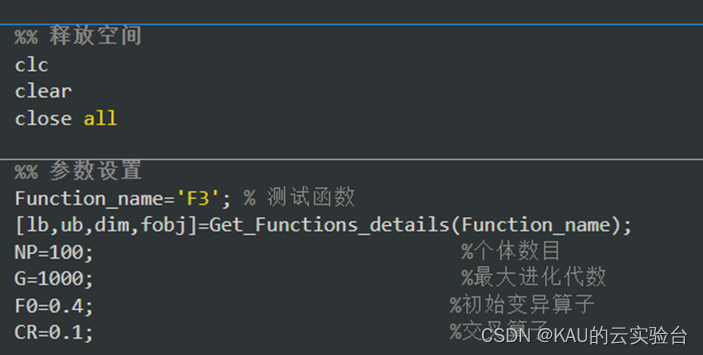

03 算法性能
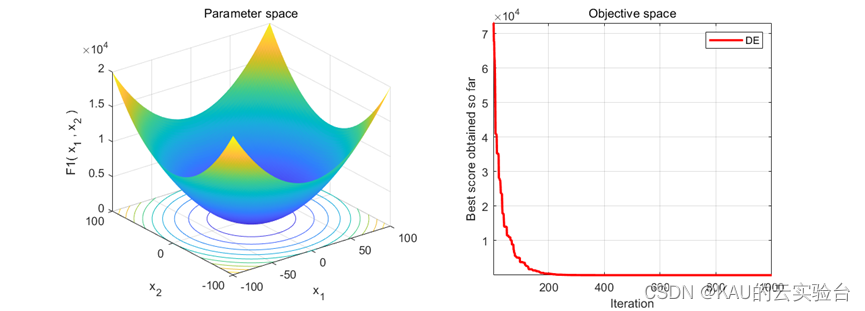
采用CEC中的测试函数来初步检验其寻优性能,在MATLAB中执行程序结果如下:
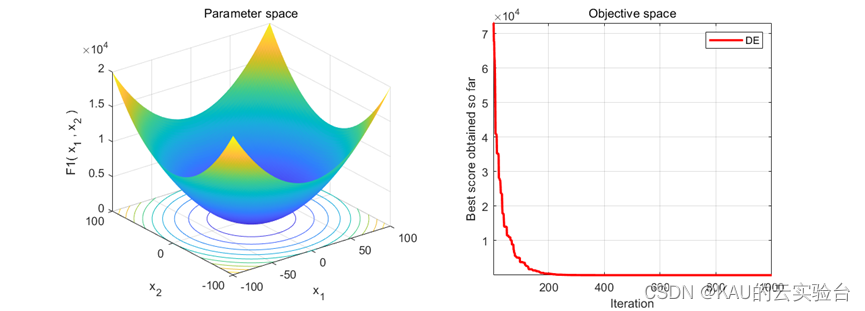
在Python中结果:
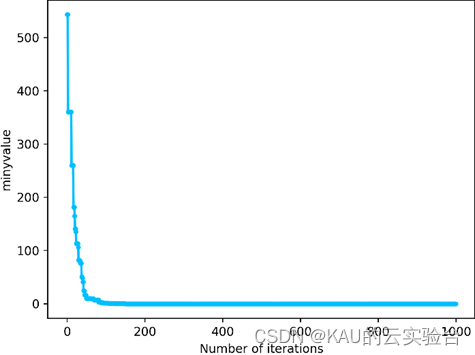
04 源码获取
在GZH(KAU的云实验台)加粗样式回复 DE 即可
DE算法具有较强的通用性,不依赖于问题信息,且原理简单,容易实现,能够利用个体的局部信息和群体的全局信息指导算法搜索,能够易于与其他算法结合,同样,DE算法也存在局部搜索能力弱、搜索效率低等缺点,为此,可采用不同的变异策略或是种群更新机制等方法提升其性能。
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看(ง •̀_•́)ง(不点也行),你们的鼓励就是我坚持的动力!若有定制需求,可私信作者。
相关文章:

超详细 | 差分进化算法原理及其实现(Matlab/Python)
差分进化(Differential Evolution,DE)算法是由美国学者Storn和 Price在1995年为求解Chebyshev多项式拟合问题而提出的。算法主要通过基于差分形式的变异操作和基于概率选择的交叉操作进行优化搜索,虽然其操作名称和遗传算法相同,但实现方法有…...

大二第三周总结(算法+生活)
算法: 题目:有效的括号 这个题目也是做过很多回了。主要就是数据结构中”栈“的应用,先进后出。 解题思路: 1.创建 Map 哈希表形成键值对映射 2.进行遍历字符串 在遍历过程中 如果 遍历到的字符c 是左括号,则入栈 pu…...

Lake Formation 和 IAM 之间的区别与联系
IAM 和 Lake Formation 都是 AWS 上的权限管理服务,且默认都是自动开启并生效的,只是如果你没有特别配置过它们,可能感觉不到它们的存在,特别是Lake Formation(后文简写为 LF),通常情况下都是“透明”的,但它确实在每次请求时进行了权限检查。本文会详细介绍一下两者之…...

音频抓取代码示例
以下是一个使用DefaultsKit库的简单爬虫程序,用于爬取音频。代码中使用了https://www.duoip.cn/get_proxy的API获取代理服务器。 import Foundation import DefaultsKit let url "https://www.douban.com/music" // 目标网站URL let proxyUrl "…...

Hexo搭建个人博客系列之环境准备
环境准备 Git Git官网,安装过程,就是一直下一步,详细的看这篇文章 Git的安装 Node.js Node.js官网 Node.js的安装 注册一个GitHub账号 安装hexo 新建一个文件夹(位置任意),运行cmd(若出现了operation not permitted,就以管理员的权限来运行cmd),运行…...

小程序技术在信创操作系统中的应用趋势:适配能力有哪些?
小程序技术在信创操作系统中的应用前景非常广阔,但也面临着一些挑战和问题。开发者需要积极应对这些挑战和问题,为信创操作系统的发展和推广做出贡献。同时,开发者也需要关注小程序技术在信创操作系统中的应用趋势,积极探索新的应…...
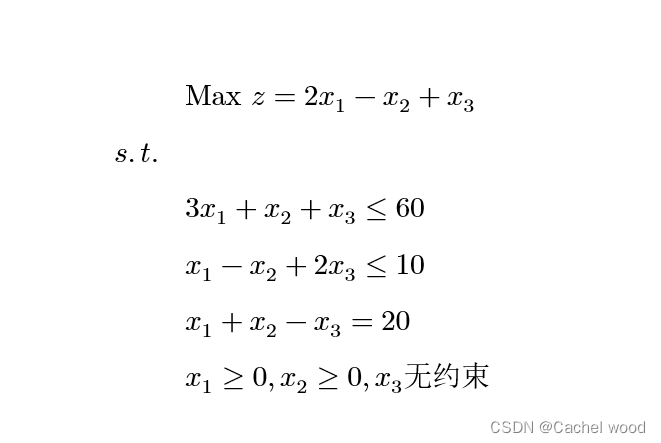
word修改公式默认字体并打出漂亮公式
文章目录 word公式简介传统方法1——mathtype传统方法2——word自带公式编辑器最简洁方法——更改word自带公式字体快捷方式效果展示 word公式简介 word自带的公式字体Cambria Math不可否认很丑,要打出latex格式的漂亮字体很困难。使用Markdown工具很多只能导出为不…...

Day 08 python学习笔记
函数 作用域 作用域:变量的访问权限 全局变量与局部变量 声明在函数外边的变量----全局变量 ----》全局作用域 函数内部的变量------局部变量 ----》局部作用域顶格创建的函数也是全局的 例: a 100def test_01():a 0b 110print…...

Qt Designer如何安装,打开方式
Qt Designer分为PyQt5 Qt Designer、PySide6 Qt Designer,下面分别介绍各自的安装方式和打开方式 首先,检查是否安装了python,使用cmd打开命令行窗口,输入: python --version若出现python的版本号,则已安…...
--让自己习惯C++)
《Effective C++》知识点(1)--让自己习惯C++
多年前看过的这本书(侯捷翻译的),忘得差不多了,重温复习一下。 1. 视C为一个语言联邦 C并不只是一个带有一组守则的一体语言;它是从四个次语言组成的联邦(federation)政府,每个次语言都有自己的规约。 次语言说明CC是C的基础&am…...
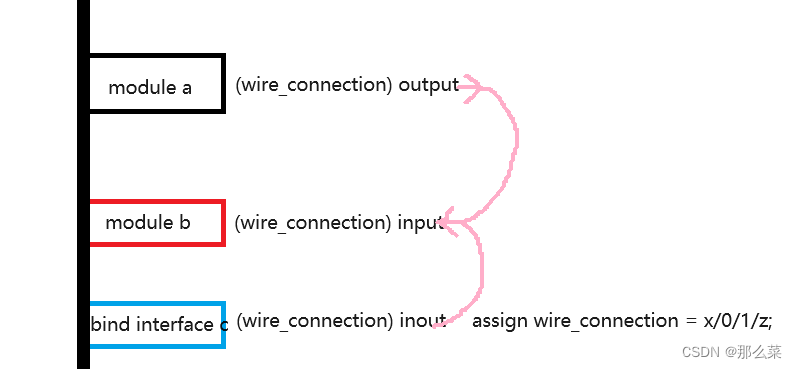
UVM 验证方法学之interface学习系列文章(八)《interface不小心引入X态问题》
前面的文章学习,想必大家都对interface 有了深入了解。大家可不要骄傲哦,俗话说:小心驶得万年船。今天,再给大家介绍一个工作中,不是经常遇到,但是一旦遇到,会让你纠结很久的事情。 前面文章提到,随着验证复杂度的不断增加,interface 的bind 的操作,是必不可少的用法…...

BBR算法的几种状态
BBR(Bottleneck Bandwidth and Round-trip propagation time)算法根据互联网的拥塞行为定义了四种状态:STARTUP、DRAIN、PROBE_BW和PROBE_RTT。下面对每种状态进行详细解释,并说明它们之间的区别: STARTUP(…...

利用jupyter进行分类
Jupyter Notebook是一个非常强大的工具,可以用于各种数据分析和机器学习任务,包括分类问题。在Jupyter Notebook中进行分类通常需要以下步骤: 导入所需的库:首先,你需要导入必要的Python库,例如NumPy、Pand…...

【LeetCode 算法专题突破】滑动窗口(⭐)
文章目录 前言1. 长度最小的子数组题目描述代码 2. 无重复字符的最长子串题目描述代码 3. 最大连续1的个数 III题目描述代码 4. 将 x 减到 0 的最小操作数题目描述代码 5. 水果成篮题目描述代码 6. 找到字符串中所有字母异位词题目描述代码 7. 串联所有单词的子串题目描述代码 …...
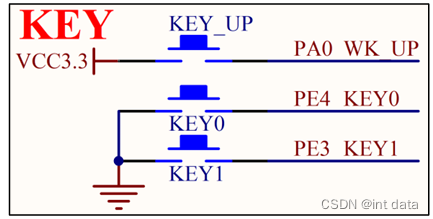
按键中断控制LED灯亮灭
EXTI—外部中断/事件控制器 EXTI(External interrupt/event controller)—外部中断/事件控制器,管理了控制器的 20 个中断/事 件线。每个中断/事件线都对应有一个边沿检测器,可以实现输入信号的上升沿检测和下降沿的 检测。EXTI可…...
YOLOV8目标检测——模型训练
文章目录 1下载yolov8([网址](https://github.com/ultralytics/ultralytics))2用pycharm打开文件3训练自己的YOLOV8数据集4run下运行完了之后没有best.pt文件5导出为onnx文件 本章内容主要解决如何训练自己的YOLOV8模型。 1下载yolov8(网址&a…...

利用dockerfile升级flink的curl
最近Nusses扫出flink镜像有CURL漏洞,才发现要更新到最新版本 8.4.0,笔者当时flink版本为: flink:1.17.1-scala_2.12-java8 官方镜像仓库:https://hub.docker.com/_/flinkapt源 我试了如上2种方法,都不能更新curl到8…...
element 日期选择器禁止选择指定日期前后时间
画圈重点:disabledDate的写法要用箭头函数,不能用普通函数写法,否则this指向就错了,会报 undefined <el-date-picker v-model"time" type"date" value-format"yyyy-MM-dd" :…...

00TD时尚女童睡衣,蕾丝边+蝴蝶结太好看了
甜美又可爱的蕾丝花边加蝴蝶结 真的一下子戳中了我的心巴, 满满的少女风真的很好看, 妥妥的可爱小公主一枚 柔软又亲肤,厚厚的很保暖 睡觉真的很舒服 还有袖口和裤脚都做了松紧设计哟!...

网络基础知识点
osi七层模型: 应用层:提供用户接口,与用户进行交互 表示层:进行数据格式的转换 会话层:建立、维护和验证会话 传输层:保证目标从源到目的地的传输(传输协议和端口号) 网络层&#x…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
