openMP学习笔记 -编程模型
OpenMP模型
gcc编译openmp指令:gcc test.cpp -o test -fopenmp
定积分计算 函数面积
给定一个定积分,计算其面积:
∫ 0 1 4.0 ( 1 + x 2 ) d x \int^{1}_{0}{\frac{4.0}{(1+x^2)}dx} ∫01(1+x2)4.0dx
omp 概念
并行区域
并行区域用于多线程并行执行指令
#pragma omp parallel
{... do lots of stuff
}//end of parallel region
临界区
临界区用于解决:内存竞争问题,该区块中的代码只能有一个线程执行,其他线程必须等待。
#pragma omp critical
{... one or more lines of code
}
栅栏
栅栏用于解决线程同步问题,通过栅栏设置的锚点,必须等所有线程均执行到该位置才能继续往下执行。
#pragma omp barrier
//... continue work栅栏通常用于这种情况,即必须在所有线程完成栅栏前的工作内容,才能继续往下执行。栅栏后的工作内容应当依赖所有线程栅栏前的工作全部完成才能执行,否则得不偿失。
因为栅栏所带来开销很大。这一点相当于cuda中的同步函数。
omp相关函数
int omp_get_num_threads(): 获取正在运行的线程数int omp_get_thread_num(): 获取线程idvoid omp_set_num_threads(int): 获取要执行的线程数double omp_get_wtime(): 返回以秒为单位的时间
串行执行
以横坐标为单位划分为指定数量的小块,取每个小块的中值作为该块的值,累加获得最终值。代码如下:
#include <stdio.h>
#include <omp.h>
#include <iostream>
static long num_steps = 100000000;
double step;
int main(){int i;double x , pi , sum=0.0;double start_time , run_time;step = 1.0 / (double)num_steps;start_time = omp_get_wtime();for (int i=0; i<num_steps; ++i) {x = (i+0.5)*step;sum += 4.0 / (1.0 +x*x);}pi = step*sum;run_time = omp_get_wtime() - start_time;std::cout<<"area result: "<<pi<<" steps: "<<num_steps<<" runtime: "<<run_time<<std::endl;return 0;
}
以padding的方式解决多线程计算总和问题
#include <stdio.h>
#include <omp.h>
#include <iostream>
#include <math.h>
#include <functional>
#define NTHREADS 12
double func(const double &x){return 4.0/(1.0+x*x);
}
template<typename FunctionType> double Area(FunctionType func,const double &start, const double &end, const long &num_steps){double width = (end-start)/num_steps;double hight[NTHREADS]={0.0};int actual_RunThreads;// omp_set_num_threads(NTHREADS);double start_time = omp_get_wtime();#pragma omp parallel{//获取线程idlong thread_ID = omp_get_thread_num();//获取实际运行的线程数if(!thread_ID) actual_RunThreads = omp_get_num_threads();for(long i = thread_ID; i<num_steps ; i+=actual_RunThreads){double x = start +(i+0.5)*width;hight[thread_ID]+=func(x);}}double hightSum=0.0;for (int i =0;i!=actual_RunThreads ; ++i) {hightSum+=hight[i]; }double runtime = omp_get_wtime()-start_time;std::cout<<"runtime: "<<runtime<<" actual_RunThreads: "<<actual_RunThreads<<std::endl;return hightSum*width;
}template<typename FunctionType, typename... Args> double AreaAgent(FunctionType func ,Args... args){return Area( func, args...);
}int main(){std::function<double(const double&)> f = func;double area = AreaAgent(f , 0.0 , 1.0 , 100000000);std::cout<<"area: "<<area<<std::endl;return 0;
}
以临界区方式计算面积总和问题
#include <stdio.h>
#include <omp.h>
#include <iostream>
#include <math.h>
#include <functional>
double func(const double &x){return 4.0/(1.0+x*x);
}
template<typename FunctionType> double Area(FunctionType func,const double &start, const double &end, const long &num_steps){//获取每块的宽度//num_steps表示分为多少块double width = (end-start)/num_steps;double sum=0.0;int actual_RunThreads;double start_time = omp_get_wtime();//并行执行区域#pragma omp parallel{double partial_sum=0.0;//获取线程idlong thread_ID = omp_get_thread_num();//获取实际运行的线程数if(!thread_ID) actual_RunThreads = omp_get_num_threads();//actual_RunThreads表示步长for(long i = thread_ID; i<num_steps ; i+=actual_RunThreads){//以块中间的函数值作为整块的面积double x = start +(i+0.5)*width;partial_sum+=func(x);}//互斥方式计算总面积,相当于原子操作#pragma omp critical{sum+=partial_sum;}}double runtime = omp_get_wtime()-start_time;std::cout<<"runtime: "<<runtime<<" actual_RunThreads: "<<actual_RunThreads<<std::endl;return sum*width;
}template<typename FunctionType, typename... Args> double AreaAgent(FunctionType func ,Args... args){return Area( func, args...);
}int main(){std::function<double(const double&)> f = func;double area = AreaAgent(f , 0.0 , 1.0 , 100000000);std::cout<<"area: "<<area<<std::endl;return 0;
}
执行时间统计
| 线程数 | 串行 | OMP | OMP消除伪共享 | OMP临界区同步 |
|---|---|---|---|---|
| 1 | 0.290821 | 2.49737 | 2.51376 | 2.50391 |
| 2 | 0.290821 | 2.46001 | 2.55435 | 1.25341 |
| 3 | 0.290821 | 2.92166 | 1.90781 | 0.991777 |
| 4 | 0.290821 | 4.09134 | 1.26799 | 0.630626 |
| 5 | 0.290821 | 3.13144 | 2.53815 | 0.627318 |
| 6 | 0.290821 | 2.93112 | 1.24541 | 0.579776 |
| 7 | 0.290821 | 2.83655 | 2.95334 | 0.527468 |
| 8 | 0.290821 | 2.9195 | 0.826844 | 0.458585 |
| 9 | 0.290821 | 2.39431 | 0.852851 | 0.409409 |
| 10 | 0.290821 | 3.20907 | 0.82156 | 0.381328 |
| 11 | 0.290821 | 3.02943 | 1.91977 | 0.352992 |
| 12 | 0.290821 | 2.95709 | 0.737233 | 0.343221 |
相关文章:

openMP学习笔记 -编程模型
OpenMP模型 gcc编译openmp指令:gcc test.cpp -o test -fopenmp 定积分计算 函数面积 给定一个定积分,计算其面积: ∫ 0 1 4.0 ( 1 x 2 ) d x \int^{1}_{0}{\frac{4.0}{(1x^2)}dx} ∫01(1x2)4.0dx omp 概念 并行区域 并行区域用于…...

【Hive SQL 每日一题】环比增长率、环比增长率、复合增长率
文章目录 环比增长率同比增长率复合增长率测试数据需求说明需求实现 环比增长率 环比增长率是指两个相邻时段之间某种指标的增长率。通常来说,环比增长率是比较两个连续时间段内某项数据的增长量大小的百分比。 环比增长率反映了两个相邻时间段内某种经济指标的变…...
)
Java设计模式之外观模式(Facade Pattern)
外观模式(Facade Pattern)是一种结构型设计模式,它提供了一个统一的接口,用于访问子系统中的一组接口。外观模式通过隐藏子系统的复杂性,简化了客户端与子系统之间的交互,提供了一个更简单、更直观的接口。…...

【大疆智图】大疆智图(DJI Terra 3.0.0)安装及使用教程
大疆智图是一款以二维正射影像与三维模型重建为主的软件,同时提供二维多光谱重建、激光雷达点云处理、精细化巡检等功能。它能够将无人机采集的数据可视化,实时生成高精度、高质量三维模型,满足事故现场、工程监测、电力巡线等场景的展示与精确测量需求。 文章目录 1. 安装D…...
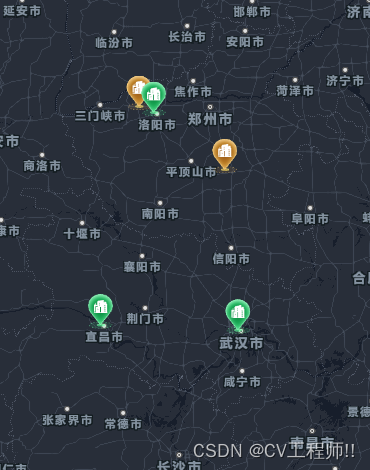
腾讯地图基本使用(撒点位,点位点击,弹框等...功能) 搭配Vue3
腾讯地图的基础注册账号 展示地图等基础功能在专栏的上一篇内容 大家有兴趣可以去看一看 今天说的是腾讯地图的在稍微一点的基础操作 话不多说 直接上代码 var marker ref(null) var map var center ref(null) // 地图初始化 const initMap () > {//定义地图中心点坐标…...
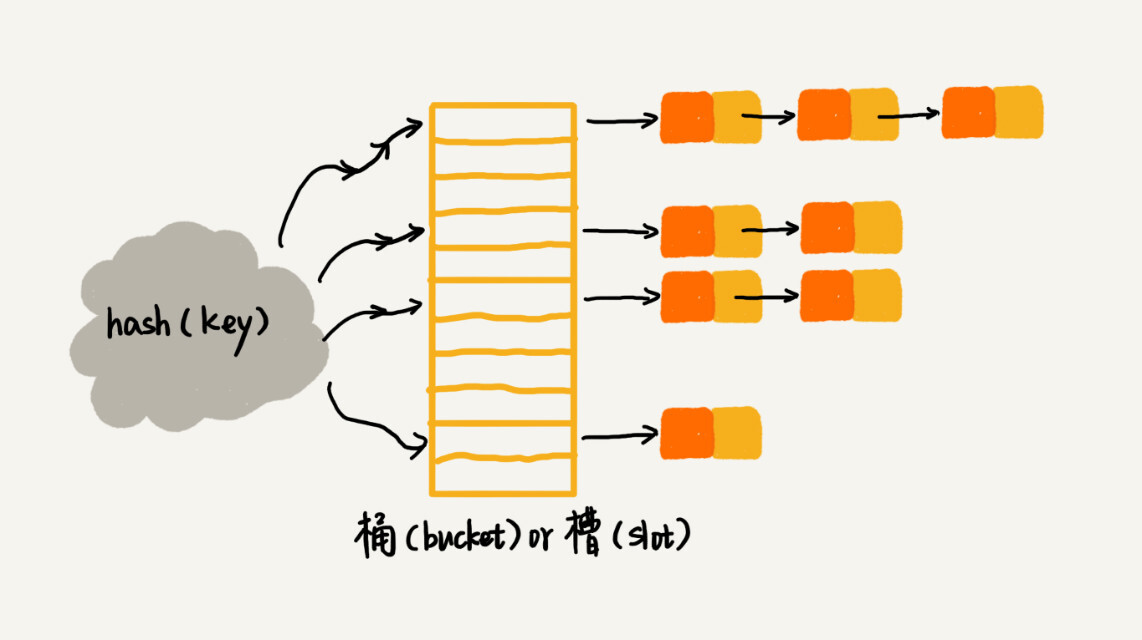
散列表:Word文档中的单词拼写检查功能是如何实现的?
文章来源于极客时间前google工程师−王争专栏。 一旦我们在Word里输入一个错误的英文单词,它就会用标红的方式提示“编写错误”。Word的这个单词拼写检查功能,虽然很小但却非常实用。这个功能是如何实现的? 散列别(Hash Table&am…...

智慧公厕蜕变多功能城市智慧驿站公厕的创新
随着城市发展的不断推进,对公共设施的便利性和智能化要求也日益提高。为满足市民对高品质、便捷、舒适的公共厕所的需求,智慧公厕行业的领航厂家广州中期科技有限公司,全新推出了一体化智慧公厕驿站。凭借着“高科技碳中和物联网创意设计新经…...

R语言清洗与处理数据常用代码段
去掉数据框df的某一列: # 删除不必要的变量 data$unnecessary_var <- NULL 选择需要的列进行读入数据框: # 选择需要的列 selected_cols <- c("col1", "col2", "col3") data <- fread("data.csv", s…...

centos 7.9 安装python 3.10的tls问题,
本地开发升级成了py3.10.6,服务器测试时安装py3.10.4 发现无法正常使用pip3 pip is configured with locations that require TLS/SSL, however the ssl module in Python is not available. 印象中py3的高版本依赖高版本的openssl,centos 7下默认的openssl为1.0.x, 问题很简…...

pytorch,tf维度理解RNN
input_t input_t.squeeze(1) 这行代码用于从 input_t 中去除尺寸为1的维度。在深度学习中,经常会出现具有额外尺寸为1的维度,这些维度通常是为了匹配模型的期望输入维度而添加的。 在这里,input_t可能具有形状 (batch_size, 1, feature_dim…...

算法刷题-数组
算法刷题 209. 长度最小的子数组-二分或者滑动窗口 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl1, ..., numsr-1, numsr] ,并返回其长度**。**如果不存在符合条件的子数…...
可视化数学分析软件 MATLAB R2021b mac中文版软件介绍
MATLAB R2021b mac作为数学类科技应用软件中首屈一指的商业数学软件,可以帮助您进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。…...

罗技摄像头左右翻转
需要下载驱动lws(我的是c310) LWS 罗技摄像头驱动下载 打开驱动程序,高级设置。有个镜像。...
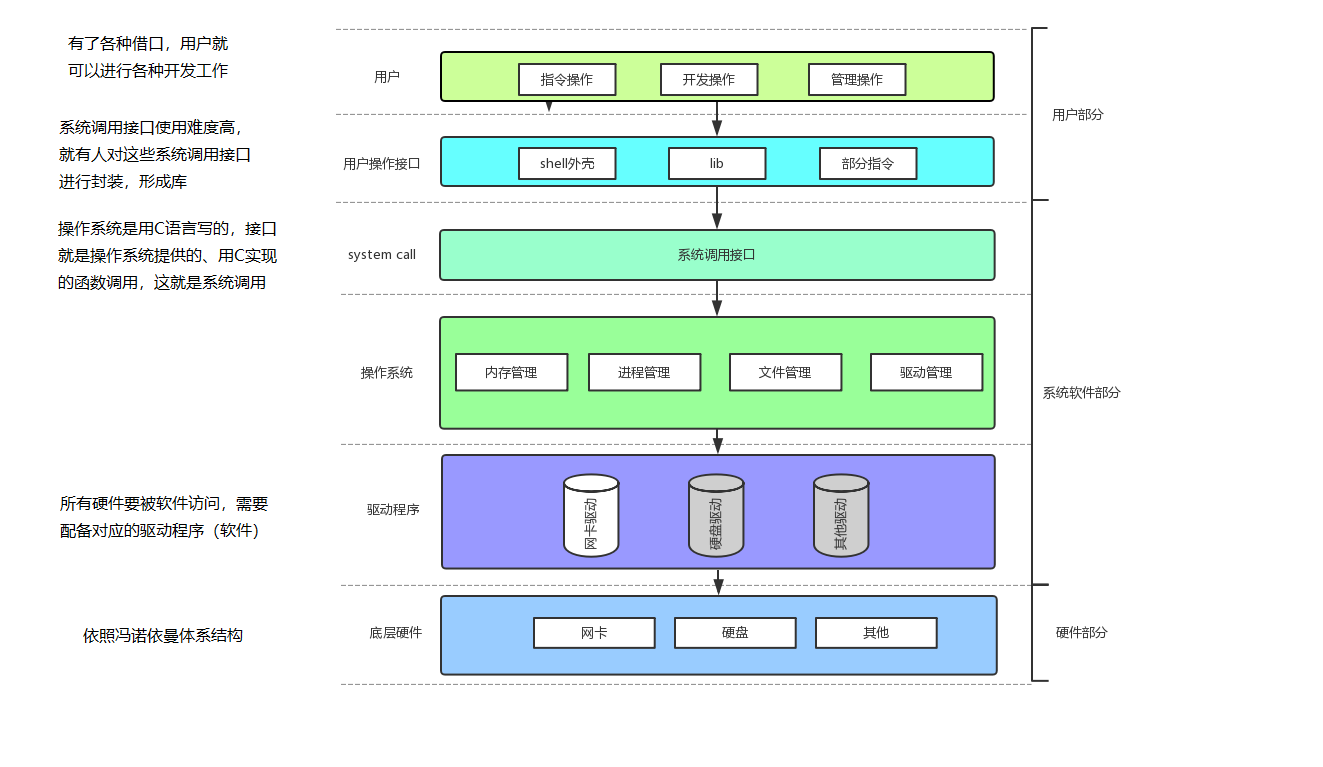
【Linux】操作系统的认识
操作系统 1. 冯诺依曼体系结构2. 操作系统 1. 冯诺依曼体系结构 冯诺依曼体系结构的介绍 冯.诺依曼结构消除了原始计算机体系中,只能依靠硬件控制程序的状况(程序作为控制器的一部分,作为硬件存在),将程序编码存储在…...

【论文阅读】(2023TPAMI)PCRLv2
目录 AbstractMethodMethodnsU-Net中的特征金字塔多尺度像素恢复多尺度特征比较从多剪切到下剪切训练目标 总结 Abstract 现有方法及其缺点:最近的SSL方法大多是对比学习方法,它的目标是通过比较不同图像视图来保留潜在表示中的不变合判别语义ÿ…...
-mapreduce task详解)
大数据学习(17)-mapreduce task详解
&&大数据学习&& 🔥系列专栏: 👑哲学语录: 承认自己的无知,乃是开启智慧的大门 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝支持一下博主哦ᾑ…...

HCIA --- DHCP服务、路由器、网络部署及基本配置
带宽计算公式: 速率 约等于 (带宽/8)*85% 网线分类: RJ-45双绞线 非屏蔽线 最佳距离100M; 民用 1000M/S 商用100000M/S 数字 光纤 光信号 RJ-11 电话线 模拟信号 同轴电缆 数字信号 光信号 数字信号--二进制 …...
手把手入门Node框架Egg.js
0.介绍 Egg.js 是一个面向企业级应用开发的 Node.js 框架,它建立在 Koa.js 之上,提供了一种更简单、灵活的开发方式。Egg.js 提供了一些默认约定和最佳实践,可以帮助开发者快速构建可靠、可扩展的应用程序。 基于 Koa.js:Egg.js …...

百度智能云推出,国内首个大模型全链路生态支持体系
在10月17日举行的百度世界2023上,百度智能云宣布,百度智能云千帆大模型服务平台已服务17000多家客户,覆盖近500个场景。 同时,新的企业和开发者还正在不断地涌入千帆,大模型调用量高速攀升。平台上既有年龄仅14岁的小…...
CUDA学习笔记(八)Branch Divergence and Unrolling Loop
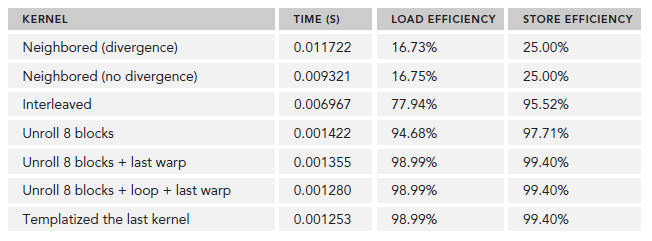
Avoiding Branch Divergence 有时,控制流依赖于thread索引。同一个warp中,一个条件分支可能导致很差的性能。通过重新组织数据获取模式可以减少或避免warp divergence(该问题的解释请查看warp解析篇)。 The Parallel Reduction …...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...
