【考研数学】线性代数第六章 —— 二次型(3,正定矩阵与正定二次型)
文章目录
- 一、基本概念
- 1.1 引例
- 1.2 正定二次型概念
- 二、正定二次型的判别
- 写在最后
一、基本概念
1.1 引例
(1)二次型 f ( x 1 , x 2 , x 3 ) = x 1 2 + 3 x 2 2 + 2 x 3 2 = X T A X f(x_1,x_2,x_3)=x_1^2+3x_2^2+2x_3^2=\pmb{X^TAX} f(x1,x2,x3)=x12+3x22+2x32=XTAX 有如下特点:
- 对任意的 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3 ,有 f ( x 1 , x 2 , x 3 ) ≥ 0 f(x_1,x_2,x_3)\geq0 f(x1,x2,x3)≥0 ;
- f ( x 1 , x 2 , x 3 ) = 0 f(x_1,x_2,x_3)=0 f(x1,x2,x3)=0 当且仅当 x 1 = x 2 = x 3 = 0 x_1=x_2=x_3=0 x1=x2=x3=0 ,或对任意 X ≠ 0 \pmb{X}\ne\pmb{0} X=0 ,有 X T A X > 0 \pmb{X^TAX}>0 XTAX>0 。
(2)二次型 f ( x 1 , x 2 , x 3 ) = x 1 2 − 2 x 1 x 2 + 4 x 2 2 + 6 x 3 2 = ( x 1 − x 2 ) 2 + 3 x 2 2 + 6 x 3 2 = X T A X f(x_1,x_2,x_3)=x_1^2-2x_1x_2+4x_2^2+6x_3^2=(x_1-x_2)^2+3x_2^2+6x_3^2=\pmb{X^TAX} f(x1,x2,x3)=x12−2x1x2+4x22+6x32=(x1−x2)2+3x22+6x32=XTAX 有如下特点:
- 对任意的 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3 ,有 f ( x 1 , x 2 , x 3 ) ≥ 0 f(x_1,x_2,x_3)\geq0 f(x1,x2,x3)≥0 ;
- f ( x 1 , x 2 , x 3 ) = 0 f(x_1,x_2,x_3)=0 f(x1,x2,x3)=0 当且仅当 x 1 = x 2 = x 3 = 0 x_1=x_2=x_3=0 x1=x2=x3=0 ,或对任意 X ≠ 0 \pmb{X}\ne\pmb{0} X=0 ,有 X T A X > 0 \pmb{X^TAX}>0 XTAX>0 。
1.2 正定二次型概念
对二次型 f ( x 1 , x 2 , ⋯ , x n ) = X T A X f(x_1,x_2,\cdots,x_n)=\pmb{X^TAX} f(x1,x2,⋯,xn)=XTAX ,若对任意 X ≠ 0 \pmb{X}\ne\pmb{0} X=0 ,总有 X T A X > 0 \pmb{X^TAX}>0 XTAX>0 ,称 X T A X \pmb{X^TAX} XTAX 为正定二次型, A \pmb{A} A 为正定矩阵。
二、正定二次型的判别
定理 1 —— 二次型 X T A X \pmb{X^TAX} XTAX 为正定二次型的充分必要条件是 A \pmb{A} A 的特征值均为正数。
定理 2 —— 二次型 X T A X \pmb{X^TAX} XTAX 为正定二次型的充分必要条件是 A \pmb{A} A 的顺序主子式都大于 0 ,即 a 11 > 0 , ∣ a 11 a 12 a 21 a 22 ∣ > 0 , ⋯ , ∣ A ∣ > 0. a_{11}>0,\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}>0,\cdots,|\pmb{A}|>0. a11>0, a11a21a12a22 >0,⋯,∣A∣>0. 定理 3 —— 设 A T = A \pmb{A^T=A} AT=A ,则 A \pmb{A} A 为正定矩阵的充分必要条件是存在可逆矩阵 B \pmb{B} B 使得 A = B T B \pmb{A=B^TB} A=BTB 。
定理 4 —— 设 A T = A \pmb{A^T=A} AT=A ,则 A \pmb{A} A 为正定矩阵的充分必要条件是 A \pmb{A} A 与 E \pmb{E} E 合同。
定理 5 —— 设 A T = A \pmb{A^T=A} AT=A ,则 A \pmb{A} A 为正定矩阵的充分必要条件是 A \pmb{A} A 的正惯性指数为 n n n 。
定理 6 —— 设 A , B \pmb{A,B} A,B 分别为 m m m 阶和 n n n 阶实对称矩阵,则 [ A 0 0 B ] \begin{bmatrix} \pmb{A} & \pmb{0} \\ \pmb{0} & \pmb{B} \end{bmatrix} [A00B] 为正定矩阵的充分必要条件为 A , B \pmb{A,B} A,B 均为正定矩阵。
二次型 f ( X ) = X T A X f(\pmb{X})=\pmb{X^TAX} f(X)=XTAX 正定的必要条件是 a i i > 0 ( i = 1 , 2 , ⋯ , n ) ; ∣ A ∣ > 0 a_{ii}>0(i=1,2,\cdots,n);|A|>0 aii>0(i=1,2,⋯,n);∣A∣>0 。
即可以先看看对角线元素和行列式是否大于 0 ,作初步判别。
若 A \pmb{A} A 为正定矩阵,则其一定可逆;且 A − 1 , A ∗ \pmb{A}^{-1},\pmb{A}^* A−1,A∗ 均正定。
若 A , B \pmb{A,B} A,B 都是正定矩阵,则 A + B \pmb{A}+\pmb{B} A+B 也是正定矩阵。
写在最后
那线性代数到这,理论也就基本结束了。
相关文章:
)
【考研数学】线性代数第六章 —— 二次型(3,正定矩阵与正定二次型)
文章目录 一、基本概念1.1 引例1.2 正定二次型概念 二、正定二次型的判别写在最后 一、基本概念 1.1 引例 (1)二次型 f ( x 1 , x 2 , x 3 ) x 1 2 3 x 2 2 2 x 3 2 X T A X f(x_1,x_2,x_3)x_1^23x_2^22x_3^2\pmb{X^TAX} f(x1,x2,x3)x123…...

【Java 进阶篇】手把手教你创建 Bootstrap 旅游网站
随着互联网的普及,旅游行业在全球范围内迅速发展。人们通过网络规划、预订和分享他们的旅行经历。因此,拥有一个令人印象深刻的旅游网站对于吸引游客和提供有用信息至关重要。在本篇博客中,我们将手把手教您如何创建一个令人兴奋的旅游网站&a…...
一百九十二、Flume——Flume数据流监控工具Ganglia单机版安装
一、目的 在安装好Flume之后,需要用一个工具可以对Flume数据传输进行实时监控,这就是Ganglia 二、Ganglia介绍 Ganglia 由 gmond、gmetad 和 gweb 三部分组成。 (一)第一部分——gmond gmond(Ganglia Monitoring Da…...

光学知识整理-偏振光
偏振光 目录基础概念基础概念的补充平面偏振光(线偏振光)部分偏振光圆偏振光椭圆偏振光菲涅耳公式相位关系 反射折射所引起的偏振态的改变斯托克斯倒逆关系重要参数 目录 基础概念 光是横波:光是电磁波,其电场分量(电场强度)E、磁场分量(磁…...

CUDA纹理内存tex1D/tex2D/tex3D函数
CUDA的tex1D是用于从一维纹理中读取数据的函数。纹理是一种特殊的内存区域,可以用来存储图像、视频或其他数据。tex1D函数可以用于从纹理中读取数据,并将其传递给CUDA程序。 tex1D函数的语法如下: float tex1D(sampler_t sampler, float te…...

【Java基础面试三十八】、请介绍Java的异常接口
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:请介绍Java的异常接口 …...

LabVIEW中的数据通信方法
LabVIEW中的数据通信方法 LabVIEW中包含多种数据通信方法,不同的方法适用于不同的场景。应该先了解概述,确保在应用程序中使用正确的数据通信方法。 数据通信类型: 数据流元素 缓冲接口 变量接口 应用场景: 在多数程序框图对…...

记调试SMBUS的心得
为什么电池电压读的不对 仔细一看是I2C读取数据的时候少了一个CLK I2C是非常严密的 读数据之后,发送 ACK,让从机准备数据 发送NACK,告诉从机别准备了 ACK和NACK的区别是啥,告诉你,就是NACK先拉高SDA,再…...

【C++】:类和对象(中)之拷贝构造函数+赋值运算符重载
拷贝构造函数 概念 在现实生活中,可能存在一个与你一样的自己,我们称其为双胞胎 那在创建对象时,可否创建一个与已存在对象一某一样的新对象呢? 拷贝构造函数:只有单个形参,该形参是对本类类型对象的引用…...
C++迭代器失效
在STL中,有些操作会导致迭代器失效,即之前获取的迭代器无法再安全地使用。这是因为这些操作可能会改变容器的结构,例如插入、删除元素等。 具体来说,以下情况下迭代器会失效: 1. 当插入或删除元素导致容器中的内存重新…...
--iotauth - IoT鉴权库, 用于生成各种云平台的参数)
LuatOS-SOC接口文档(air780E)--iotauth - IoT鉴权库, 用于生成各种云平台的参数
iotauth.aliyun(product_key, device_name,device_secret,method,cur_timestamp) 阿里云物联网平台三元组生成 参数 传入值类型 解释 string product_key string device_name string device_secret string method 加密方式,”hmacmd5” “hmacsha1” “hmacsha256”…...
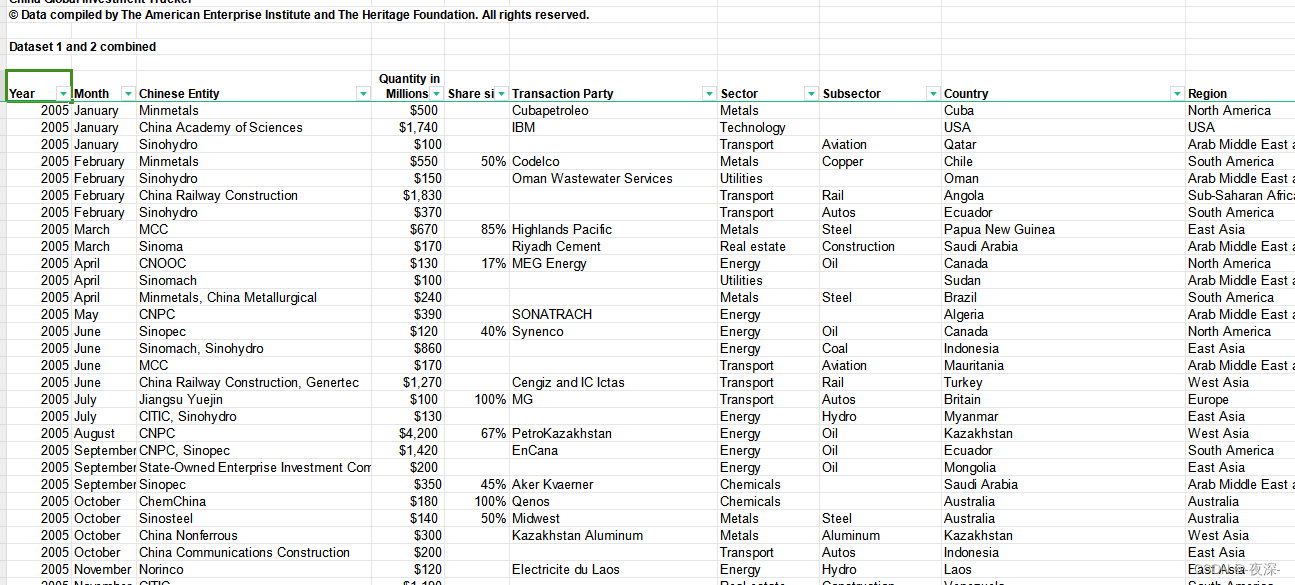
2005.6-2018.6月中国企业OFDI微观数据
2005.6-2018.6月中国企业OFDI微观数据 1、时间:2005.6-2018.6 2、范围:公司 3、指标:Year、Month、Chinese Entity、 Quantity in Millions 、Share size、Transaction Party、Sector、Subsector、Country、Region、BRI 4、数据解释&…...

Spring和SpringBoot学习
Spring和SpringBoot学习 Spring中常用注解及其作用 Spring中常用注解及其作用 SpringBoot注解扫描范围 SpringBoot | ComponentScan()注解默认扫描包范围分析 spring boot的包扫描范围 springBoot的自动扫描包范围 SpringBoot中new对象不能自动注入对象 SpringBoot中new对…...
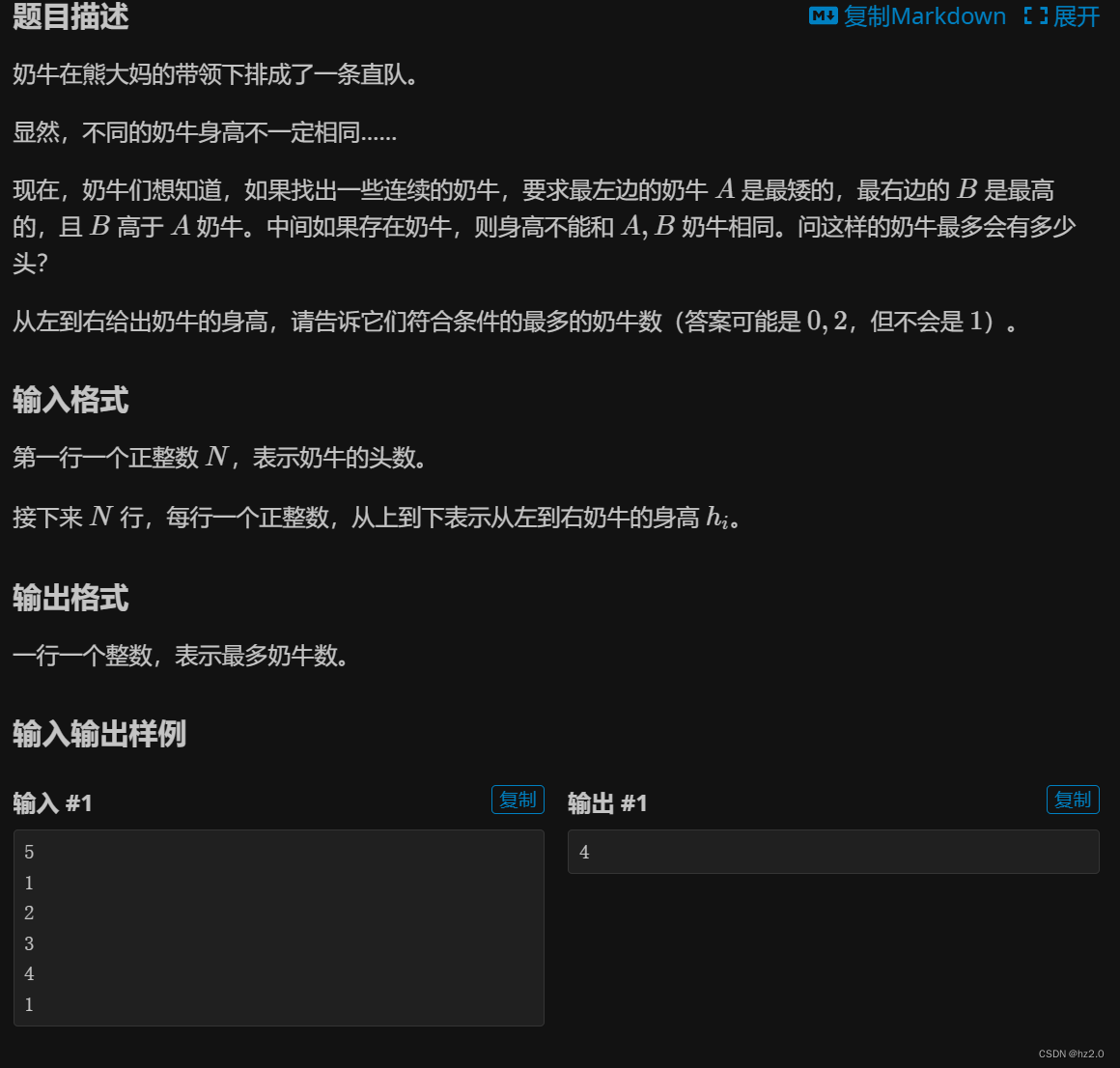
P6510 奶牛排队
题目 P6510 奶牛排队 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 思路 1.dp求最大。(dp即前后关联)arr[]用于存储输入的数据,brr[i]用于存储以第i头牛为右端点的队列最大值。 2.数组空间不够大,我们可以自己开辟对空间&…...
修改ConsoleApplication17_2项目实现oss上线
首先创建号oss,上传文件,复制临时链接 木马内写 可以看到能成功上线但是有个问题就是占用cpu大小为9%左右,这里我用的是腾讯云oss实现的,用阿里云oss实现也是9%左右 我再次进行url的aes加密 还是百分之9左右, 这里…...
Android学习之路(21) 进程间通信-AIDL与Servce基本使用
Service 与 Thread 和 进程 之间的关系 进程:应用程序在内存中分配的空间。(正在运行中的程序)线程:负责程序执行的单元,也称为执行路径。(需要线程来执行代码)。一个进程至少包含一条线程&…...
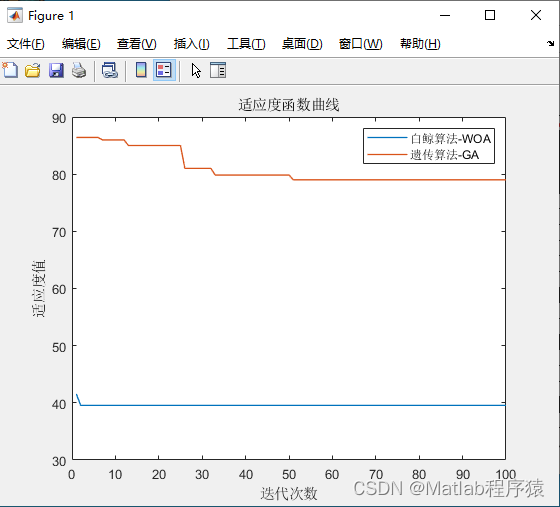
【MATLAB源码-第54期】基于白鲸优化算法(WOA)和遗传算法(GA)的栅格地图路径规划最短路径和适应度曲线对比。
操作环境: MATLAB 2022a 1、算法描述 1.白鲸优化算法(WOA): 白鲸优化算法是一种受白鲸捕食行为启发的优化算法。该算法模拟了白鲸群体捕食的策略和行为,用以寻找问题的最优解。其基本思想主要包括以下几点&#x…...

关于计算机找不到vcomp140.dll无法继续执行怎么修复
在计算机使用过程中,我们可能会遇到各种问题,其中之一就是vcomp140.dll文件丢失。vcomp140.dll是一个动态链接库文件,它通常用于支持软件运行和系统功能。当这个文件丢失时,可能会导致程序无法正常运行,甚至系统出现错…...
qt-C++笔记之信号与槽
qt-C笔记之信号与槽 code review! 本文抄自公众号:嵌入式小生 文章目录 qt-C笔记之信号与槽一.信号2.1.信号的发出2.2.信号的处理 二.槽函数2.1.带有默认参数的信号和槽函数2.2.使用QObject::connect()将信号连接到槽函数的三种方法2.2.1.第一种方法:使…...
linux安装visual studio code
下载 https://code.visualstudio.com/ 下载.deb文件 安装 假如文件被下载到了 /opt目录下 进入Opt目录,右键从当前目录打开终端。 输入下面的安装命令。 sudo apt-get install ./code_1.83.1-1696982868_amd64.deb 安装成功。 配置 打开 visual studio cod…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
