当前位置： 首页 > news >正文

双势阱模型

news 2026/2/10 20:28:45
  • 双势阱模型

原子钟

  • 传统的原子钟利用氨分子
    • 由于隧道效应，上顶点的氮原子可以贯穿三个氢原子形成的势垒，到达下顶点
    • 对体系注入微波能量后，氮原子在上下定点之间振荡，体系的能量在两个稳定态之间交替变换，其振荡频率决定了氨分子钟的频率标准
    • 2012年诺贝尔奖----离子钟

双势垒模型：低势垒

V(x)=\left\{\begin{matrix} \infty&|x|\geq L\\ 0&a< |x|< L\\ V_0&|a|\leq a \end{matrix}\right.

V_0<E

  • 微操之后，体系存在无穷多个本征态
  • 体系在L\rightarrow \infty 的极限下变为连续谱

双势垒模型：高势垒

V_0>E

量子振荡现象

\Phi(x,t)=\frac{1}{\sqrt{2}}[\phi_1(x)exp(-\frac{i}{\hbar}E_1t)-\phi_2(x)exp(-\frac{i}{\hbar}E_2t)]

  • 由复变函数的知识得：e^{i\theta}=e^{i(\theta+2\pi)}
  • 量子体系振荡频率：v=\frac{E_2-E_1}{2\pi \hbar}
  • 粒子质量，势垒宽度，本征能量越高，振荡频率越低

相关文章：

双势阱模型

双势阱模型 原子钟 传统的原子钟利用氨分子 由于隧道效应&#xff0c;上顶点的氮原子可以贯穿三个氢原子形成的势垒&#xff0c;到达下顶点对体系注入微波能量后&#xff0c;氮原子在上下定点之间振荡&#xff0c;体系的能量在两个稳定态之间交替变换&#xff0c;其振荡频率决…...

编程日记 2023/10/22 22:21:40

文献阅读：The Reversal Curse: LLMs trained on “A is B” fail to learn “B is A”

文献阅读&#xff1a;The Reversal Curse: LLMs trained on “A is B” fail to learn “B is A” 1. 文章简介2. 实验 & 结果考察 1. finetune实验2. 真实知识问答 3. 结论 & 思考 文献链接&#xff1a;https://arxiv.org/abs/2309.12288 1. 文章简介 这篇文章是前…...

编程日记 2023/10/22 22:20:39

真实感受：是智能家居在选择合适的技术！

科技从来都是为了让我们的生活更加的简单、舒适&#xff0c;而智能家居的智能&#xff0c;体现在如何更更更方便的使用我需要控制的家居。 例如&#xff1a;下班躺在床上想休息&#xff0c;房间和大厅的灯还开着&#xff0c;这时你会选择什么产品躺着解决问题&#xff1f; 红外…...

编程日记 2023/10/22 22:19:38

前端 TS 快速入门之二：接口

1. 接口有什么用 通过 interface 定义接口。 检测对象的属性&#xff0c;不会去检查属性的顺序&#xff0c;只要相应的属性存在并且类型也是对的就可以。 interface IPerson {name: string;age: number; } function say(person: IPerson): void {console.log(my name is ${pers…...

编程日记 2023/10/22 22:18:36

论文生成器（论文、文献综述、开题报告……），Java、Python、C++

“让论文生成器为您省时省力&#xff0c;轻松写出高质量的论文&#xff01;” 2022年&#xff0c;腾讯全球数字生态大会腾讯云智能专场发布。 链接&#xff1a;http://xiezuo.saiertewl.cn/tb/xrWQed?dCodeh1xDrXmuhZbKPKgI&couponCodexiaoweilunwen...

编程日记 2023/10/22 22:17:35

【Java基础面试三十六】、遇到过异常吗，如何处理？

文章底部有个人公众号&#xff1a;热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享&#xff1f; 踩过的坑没必要让别人在再踩&#xff0c;自己复盘也能加深记忆。利己利人、所谓双赢。 面试官&#xff1a;遇到过异常吗&#xff0…...

编程日记 2023/10/22 22:16:33

DASCTF-CBCTF-2023 Crypto部分复现

文章目录 EzRSACB backpack 这次比赛没打&#xff0c;记错时间了&#xff0c;看了一下&#xff0c;如果去做的话大概也只能做出那两道简单的题&#xff0c;还是太菜啦 EzRSA 题目描述&#xff1a; from Crypto.Util.number import * import random from gmpy2 import * from …...

编程日记 2023/10/22 22:15:30

为什么要做字节对齐 alignment？

下面这段 C 代码的输出是什么&#xff1f;定义的 Type 占用的字节数&#xff08;下面简称为字节数&#xff09;是多少呢&#xff1f; #include <iostream>struct Type {char a;int b; };int main(void) {std::cout << sizeof(Type) << \n; }经过编译运行&am…...

编程日记 2023/10/22 22:14:29

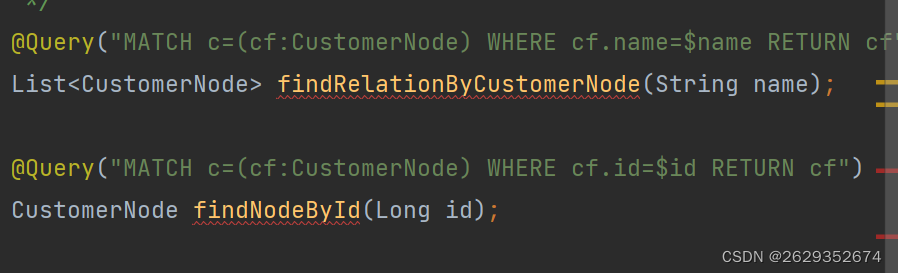
（零基础学习）Neo4j+Spring boot 自行定义属性

前置知识 1.Neo4j :属性 节点和关系都可以设置自己的属性。 属性是由Key-Value键值对组成&#xff0c;键名是字符串。属性值是要么是原始值&#xff0c;要么是原始值类型的一个数组。比如String&#xff0c;int和iint[]都是合法的。 注意 null不是一个合法的属性值。 Nulls能…...

编程日记 2023/10/22 22:13:29

【JavaEE】Java的文件IO

文件IO操作 Linux 下的文件操作讲解Java中的文件操作 -- 对文件的增删改查Java中对文件内容的操作 -- 读写操作使用案例 Linux 下的文件操作讲解 在我的Linux栏目下有, 如有需要, 点击下面进行跳转: 内存级文件系统语言级别的文教操作磁盘文件 Java中的文件操作 – 对文件的…...

编程日记 2023/10/22 22:12:28

域名解析与记录

域名解析是将域名转换为IP的过程&#xff0c;使得人们能够直接通过域名访问网站&#xff0c;而不用记繁琐的IP地址信息。而在域名解析中&#xff0c;CNAME记录和A记录是两个不同的记录类型。 A记录&#xff08;Address Record&#xff0c;地址记录&#xff09;是指将一个域名解…...

编程日记 2023/10/22 22:11:26

Android 13.0 第三方无源码apk授予QUERY_ALL_PACKAGES等其他权限的方法

1.概述 在13.0的系统产品中，对于内置第三方低版本app时，会有某些权限的冲突，导致在启动app时，崩溃掉，在查询相关日志发现是报权限的问题，所以就需要在安装解析app的时候，授予权限 2.第三方无源码apk授予QUERY_ALL_PACKAGES等其他权限的方法的核心类 /frameworks/base…...

编程日记 2023/10/22 22:10:25

【CSS】gird 网格

网格&#xff08;Grid&#xff09;是一种基于列数的布局系统&#xff0c;它可以帮助开发者创建具有水平和垂直分隔的页面布局。在CSS中&#xff0c;Grid是一种非常强大的布局工具&#xff0c;可以轻松地创建复杂的布局结构。Grid的主要属性包括&#xff1a; grid-template-col…...

编程日记 2023/10/22 22:09:24

（未完待续）【Netty专题】Netty实战与核心组件详解

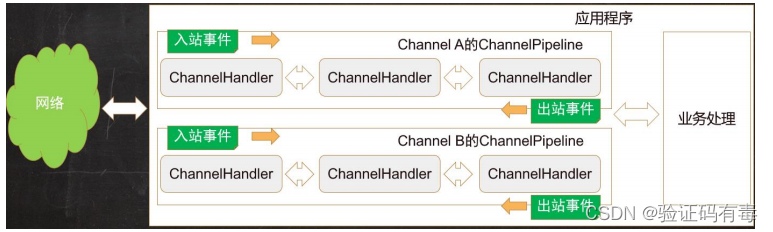
目录 前言阅读对象阅读导航前置知识课程内容一、Netty简介1.1 Netty是什么1.2 Netty有什么优势 二、第一个Netty程序2.1 Netty简单使用示例2.2 代码解读2.3 Netty的特性2.3.1 Netty的事件 2.4 Netty线程模型 三、Netty核心组件详解&#xff08;未完待续&#xff09;3.1 EventLo…...

编程日记 2023/10/22 22:08:23

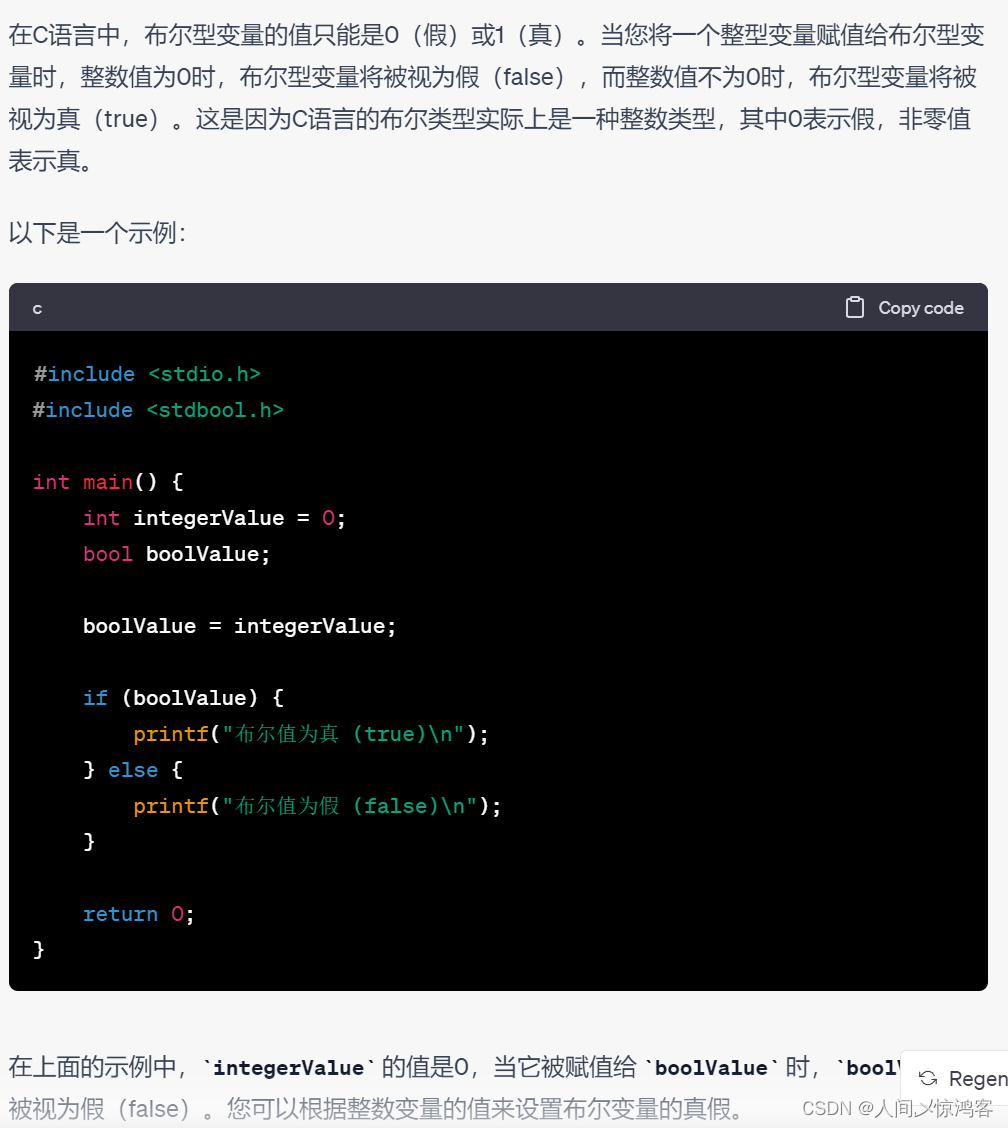
“第四十五天” 数据结构基本概念

目前看的有关数据结构的课&#xff0c;估计这周就看完了&#xff0c;但感觉差很多&#xff0c;还是和c一样&#xff0c;这样过一下吧。但可能比较急&#xff0c;目前是打算争取寒假回家之前把四大件都先大致过一遍。 数据结构里面有很多新的定义和概念&#xff0c;学到现在&am…...

编程日记 2023/10/22 22:07:22

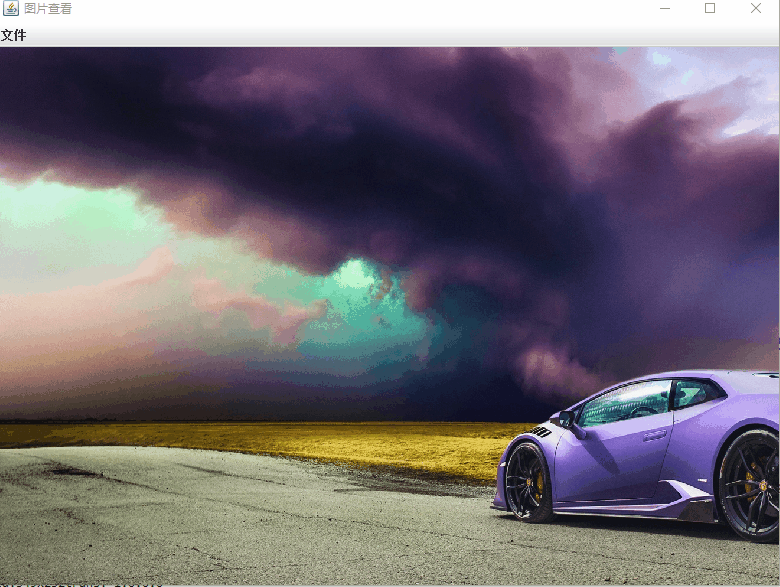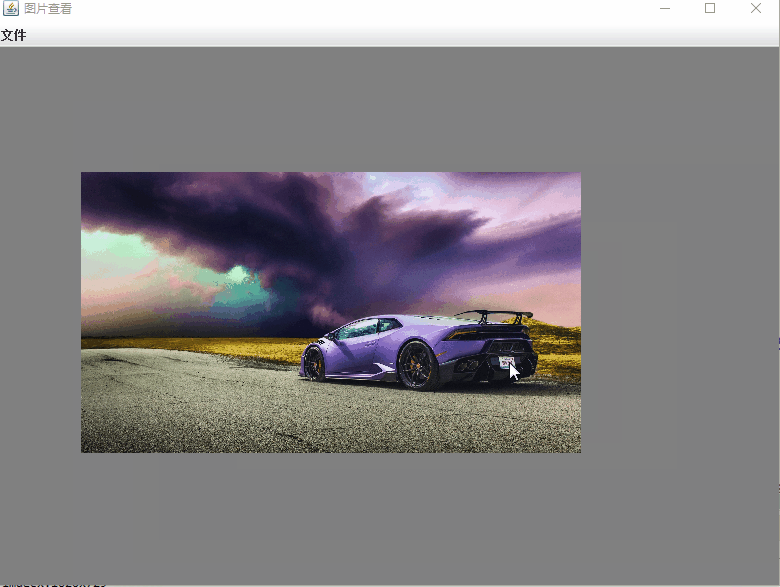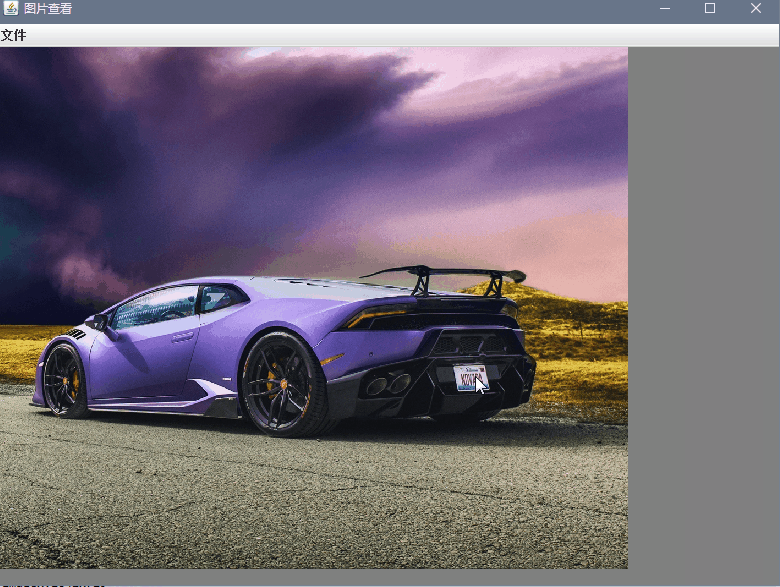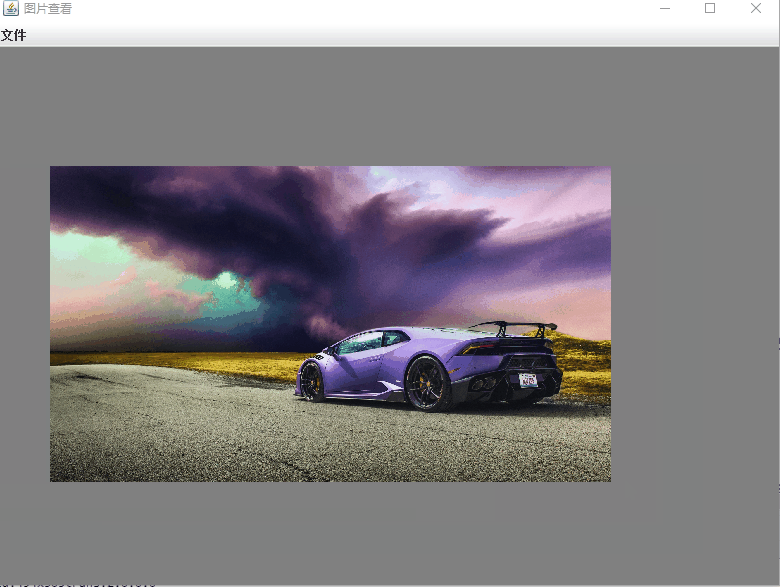
《java 桌面软件开发》swing 以鼠标为中心放大缩小移动图片

swing 使用Graphic2D 绘制图片&#xff0c;要实现对图片进行缩放和自由拖动。 1.以鼠标所在的位置为中心&#xff0c;滚轮控制缩放 2.缩放后再支持鼠标拖动。 基本原理&#xff1a; 利用scale() 函数。进行缩放。但是要注意的地方是&#xff0c;如果是在 public void paintCom…...

编程日记 2023/10/22 22:06:21

浅析人脸活体检测技术的功能及几种分类

在日常生活工作中&#xff0c;出现了人脸验证、人脸支付、人脸乘梯、人脸门禁等等常见的应用场景。这说明人脸识别技术已经在门禁安防、金融行业、教育医疗等领域被广泛地应用&#xff0c;人脸识别技术的高速发展与应用同时也出现不少质疑。其中之一就是人脸识别很容易被照片、…...

编程日记 2023/10/22 22:05:17

【Java基础面试三十五】、谈谈你对面向接口编程的理解

文章底部有个人公众号&#xff1a;热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享&#xff1f; 踩过的坑没必要让别人在再踩&#xff0c;自己复盘也能加深记忆。利己利人、所谓双赢。 面试官&#xff1a;谈谈你对面向接口编程的…...

编程日记 2023/10/22 22:04:16

利用TreeMap来达成离散化的目的

假如有一些奶牛&#xff0c;他们有种类的区别&#xff0c;我们设黑色奶牛的id为1000010000&#xff0c;白色为1&#xff0c;诸如此类以此类推还有红色等各种颜色&#xff0c;接下来给你一群奶牛的颜色id让你统计每种颜色的奶牛有几头。 如过我们使用数组显然1000010000会爆空间…...

编程日记 2023/10/22 22:03:15

PG14安装_rpm方式

一、前期准备 发现生产环境有用rpm安装&#xff0c;故整理安装rpm安装步骤&#xff0c;目的是准备walminer恢复数据用的环境 二、安装包下载 https://download.postgresql.org/pub/repos/yum/ 含多个版本 https://download.postgresql.org/pub/repos/yum/14/redhat/rhel-7-x…...

编程日记 2023/10/22 22:02:14

通过Wrangler CLI在worker中创建数据库和表

官方使用文档&#xff1a;Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后&#xff0c;会在本地和远程创建数据库&#xff1a; npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库&#xff1a; 现在&#xff0c;您的Cloudfla…...

编程新知 2026/1/31 6:18:08

Mybatis逆向工程，动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件

今天呢&#xff0c;博主的学习进度也是步入了Java Mybatis 框架&#xff0c;目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学&#xff0c;希望能对大家有所帮助&#xff0c;也特别欢迎大家指点不足之处&#xff0c;小生很乐意接受正确的建议&…...

编程新知 2026/1/31 15:00:15

汽车生产虚拟实训中的技能提升与生产优化​

在制造业蓬勃发展的大背景下&#xff0c;虚拟教学实训宛如一颗璀璨的新星&#xff0c;正发挥着不可或缺且日益凸显的关键作用&#xff0c;源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例&#xff0c;汽车生产线上各类…...

编程新知 2026/1/27 7:46:36

【git】把本地更改提交远程新分支feature_g

创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

编程新知 2025/12/13 4:20:30

深入解析C++中的extern关键字：跨文件共享变量与函数的终极指南

&#x1f680; C extern 关键字深度解析&#xff1a;跨文件编程的终极指南 &#x1f4c5; 更新时间&#xff1a;2025年6月5日 &#x1f3f7;️ 标签&#xff1a;C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言&#x1f525;一、extern 是什么&#xff1f;&…...

编程新知 2026/2/1 6:50:07

学习STC51单片机32（芯片为STC89C52RCRC）OLED显示屏2

每日一言 今天的每一份坚持&#xff0c;都是在为未来积攒底气。 案例&#xff1a;OLED显示一个A 这边观察到一个点&#xff0c;怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 &#xff1a; 如果代码里信号切换太快&#xff08;比如 SDA 刚变&#xff0c;SCL 立刻变&#…...

编程新知 2026/2/6 0:50:24

sipsak：SIP瑞士军刀！全参数详细教程！Kali Linux教程！

简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求&#xff0c;并检查收到的响应。它以以下模式之一…...

编程新知 2026/1/29 8:51:33

Netty从入门到进阶（二）

二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架&#xff0c;用于…...

编程新知 2026/1/26 5:44:16

在树莓派上添加音频输入设备的几种方法

在树莓派上添加音频输入设备可以通过以下步骤完成&#xff0c;具体方法取决于设备类型&#xff08;如USB麦克风、3.5mm接口麦克风或HDMI音频输入&#xff09;。以下是详细指南&#xff1a; 1. 连接音频输入设备 USB麦克风/声卡&#xff1a;直接插入树莓派的USB接口。3.5mm麦克…...

编程新知 2025/11/22 14:54:34

热烈祝贺埃文科技正式加入可信数据空间发展联盟

2025年4月29日&#xff0c;在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上&#xff0c;可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞&#xff0c;强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

编程新知 2026/2/7 20:23:55