DASCTF-CBCTF-2023 Crypto部分复现
文章目录
- EzRSA
- CB backpack
这次比赛没打,记错时间了,看了一下,如果去做的话大概也只能做出那两道简单的题,还是太菜啦
EzRSA
题目描述:
from Crypto.Util.number import *
import random
from gmpy2 import *
from libnum import *
from flag import flagdef padding(f):random_chars = bytes([random.randint(0, 255) for _ in range(32)])f = f + random_charsreturn fdef guess_p(p):e = 65537P = pn1 = getPrime(512)*getPrime(512)with open('enc.txt', 'w+') as f:while jacobi(2,n1) == 1:n1 = getPrime(512)*getPrime(512)while P:pad = random.randint(0, 2**2023)**2 message = pad << 1 + P % 2cipher = pow(message, e, n1)f.write(str(cipher)+'n')P //= 2print("n1 = "+ str(n1) ) def guess_q(q):def encrypt(q, n):e = random.randint(1000,2000)noise = random.randint(0, n - 1)c = pow(q+noise,e,n)return e, noise,c n2 = getPrime(512)*getPrime(512)e1, noise1, c1 = encrypt(q, n2)e2, noise2, c2 = encrypt(q, n2)print("n2 = "+ str(n2) ) print('(e1, noise1, c1) =', (e1,noise1,c1))print('(e2, noise2, c2) =', (e2,noise2,c2))
p = getPrime(512)
q = getPrime(512)n = p*q
guess_p(p)
guess_q(q)
e = 0x10001
flag = padding(flag)
m = bytes_to_long(flag)
c = pow(m,e,n)print("c = " + str(c))
'''
n1 = 65634094430927080732256164808833233563732628654160389042977689628512527168256899310662239009610512772020503283842588142453533499954947692968978190310627721338357432052800695091789711809256924541784954080619073213358228083200846540676931341013554634493581962527475555869292091755676130810562421465063412235309
n2 = 103670293685965841863872863719573676572683187403862749665555450164387906552249974071743238931253290278574192713467491802940810851806104430306195931179902098180199167945649526235613636163362672777298968943319216325949503045377100235181706964846408396946496139224344270391027205106691880999410424150216806861393
(e1, noise1, c1) = (1743, 44560588075773853612820227436439937514195680734214431948441190347878274184937952381785302837541202705212687700521129385632776241537669208088777729355349833215443048466316517110778502508209433792603420158786772339233397583637570006255153020675167597396958251208681121668808253767520416175569161674463861719776, 65643009354198075182587766550521107063140340983433852821580802983736094225036497335607400197479623208915379722646955329855681601551282788854644359967909570360251550766970054185510197999091645907461580987639650262519866292285164258262387411847857812391136042309550813795587776534035784065962779853621152905983)
(e2, noise2, c2) = (1325, 35282006599813744140721262875292395887558561517759721467291789696459426702600397172655624765281531167221787036009507833425145071265739486735993631460189629709591456017092661028839951392247601628468621576100035700437892164435424035004463142959219067199451575338270613300215815894328788753564798153516122567683, 50327632090778183759544755226710110702046850880299488259739672542025916422119065179822210884622225945376465802069464782311211031263046593145733701591371950349735709553105217501410716570601397725812709771348772095131473415552527749452347866778401205442409443726952960806789526845194216490544108773715759733714)
c = 124349762993424531697403299350944207725577290992189948388824124986066269514204313888980321088629462472088631052329128042837153718129149149661961926557818023704330462282009415874674794190206220980118413541269327644472633791532767765585035518183177197863522573410860341245613331398610013697803459403446614221369
'''
题目分析:
gen_q:
看到jacobi(2,n1)便知道是二次剩余的知识
c = ( 2 ∗ a 2 ) e ,当 P % 2 = 0 c = ( 2 ∗ a 2 + 1 ) e ,当 P % 2 = 1 c ( n 1 − 1 ) / / 2 ≡ ( 2 ∗ a 2 ) e ∗ ( n 1 − 1 ) / / 2 ≡ − 1 ∗ 1 m o d n 1 ⇒ j a c o b i ( e n c i , n 1 ) = − 1 , p = 0 + p c = (2 * a^2)^e ,当P \% 2 = 0\\ c = (2 * a^2 + 1)^e,当P \% 2 = 1\\ c^{(n1 - 1) // 2} \equiv (2 * a^2)^{e *(n1 - 1) //2} \equiv -1 * 1 \mod n1\\ \Rightarrow jacobi(enc_i,n1) = -1,p = 0 + p\\ c=(2∗a2)e,当P%2=0c=(2∗a2+1)e,当P%2=1c(n1−1)//2≡(2∗a2)e∗(n1−1)//2≡−1∗1modn1⇒jacobi(enci,n1)=−1,p=0+p
gen_q:
相关消息攻击直接解啦
exp:
import binascii
import libnum
from gmpy2 import *
from Crypto.Util.number import *
n1 = 65634094430927080732256164808833233563732628654160389042977689628512527168256899310662239009610512772020503283842588142453533499954947692968978190310627721338357432052800695091789711809256924541784954080619073213358228083200846540676931341013554634493581962527475555869292091755676130810562421465063412235309
(e1, noise1, c1) = (1743, 44560588075773853612820227436439937514195680734214431948441190347878274184937952381785302837541202705212687700521129385632776241537669208088777729355349833215443048466316517110778502508209433792603420158786772339233397583637570006255153020675167597396958251208681121668808253767520416175569161674463861719776, 65643009354198075182587766550521107063140340983433852821580802983736094225036497335607400197479623208915379722646955329855681601551282788854644359967909570360251550766970054185510197999091645907461580987639650262519866292285164258262387411847857812391136042309550813795587776534035784065962779853621152905983)
(e2, noise2, c2) = (1325, 35282006599813744140721262875292395887558561517759721467291789696459426702600397172655624765281531167221787036009507833425145071265739486735993631460189629709591456017092661028839951392247601628468621576100035700437892164435424035004463142959219067199451575338270613300215815894328788753564798153516122567683, 50327632090778183759544755226710110702046850880299488259739672542025916422119065179822210884622225945376465802069464782311211031263046593145733701591371950349735709553105217501410716570601397725812709771348772095131473415552527749452347866778401205442409443726952960806789526845194216490544108773715759733714)
c = 124349762993424531697403299350944207725577290992189948388824124986066269514204313888980321088629462472088631052329128042837153718129149149661961926557818023704330462282009415874674794190206220980118413541269327644472633791532767765585035518183177197863522573410860341245613331398610013697803459403446614221369
n2 = 103670293685965841863872863719573676572683187403862749665555450164387906552249974071743238931253290278574192713467491802940810851806104430306195931179902098180199167945649526235613636163362672777298968943319216325949503045377100235181706964846408396946496139224344270391027205106691880999410424150216806861393ciphers = []
with open('enc.txt') as f:for line in f.read().split('n'):if line.strip():ciphers.append(int(line.strip()))p = ''
for i in ciphers:if jacobi(i,n1) == -1:p = '0' + pelse:p = '1' + pp = int(p,2)def franklinReiter(n,e1,e2,c1,c2,noise1,noise2):PR.<x> = PolynomialRing(Zmod(n))g1 = (x + noise1)^e1 - c1g2 = (x + noise2)^e2 - c2def gcd(g1, g2):while g2:g1, g2 = g2, g1 % g2return g1.monic() # return -gcd(g1, g2)[0]q=franklinReiter(n2,e1,e2,c1,c2,noise1,noise2)
q = 13189337905641321257372188436353844418280745284875462357019668708167547026960641869513283218672677712590326347601424108528959315675307896082223561007980457
p = 9473204278465588641589315677772678997836862033858760337441231265335880892205102590571357305720744128962068300763212493598006400853597404586755248901932203
e = 0x10001
phi = (p - 1) * (q - 1)
d = inverse(e,phi)
print(long_to_bytes(int(pow(c,d,p * q))))
# DASCTF{W05-y03r_m2st1r-j2c0b1_2nd_p01yn0mi2l!}
CB backpack
题目描述:
from random import shuffledef gen_e():e = []for i in range(8):ee = [0]*3+[1]*3shuffle(ee)e += eereturn ee = gen_e()
nbit = len(e) # 48
flag = 'DASCTF{'+sha256(''.join([str(i) for i in e]).encode()).hexdigest()+'}'a = [randint(1,2^nbit) for i in range(nbit)]re = 0
for i in range(nbit):re += e[i]*a[i]print(a)
print(re)
题目分析:
一开始看到,感觉很熟悉啊,这不妥妥的背包加密吗,结果。。。是我想简单了
又涉及到了知识盲区,跟着大佬的wp做了一遍,学习到了
总的来说就是数据给的不够大,直接用背包格解出不来,需要爆破几位,通过jsdn测试密度是否达标(d < 0.9408)
测试了一下,得爆破10位以上才能出结果,尽管爆破8位也满足d < 0.9408,但确实是得不到
这样的话我爆破12位吧
from math import *
n = 37
a = [65651991706497, 247831871690373, 120247087605020, 236854536567393, 38795708921144, 256334857906663, 120089773523233, 165349388120302, 123968326805899, 79638234559694, 259559389823590, 256776519514651, 107733244474073, 216508566448440, 39327578905012, 118682486932022, 263357223061004, 132872609024098, 44605761726563, 24908360451602, 237906955893793, 204469770496199, 7055254513808, 221802659519968, 169686619990988, 23128789035141, 208847144870760, 272339624469135, 269511404473473, 112830627321371, 73203551744776, 42843503010671, 118193938825623, 49625220390324, 230439888723036, 241486656550572, 107149406378865, 233503862264755, 269502011971514, 181805192674559, 152612003195556, 184127512098087, 165959151027513, 188723045133473, 241615906682300, 216101484550038, 81190147709444, 124498742419309]
a = a[11:]
d = n / log2(max(a))
N = ceil(1 / 2 * sqrt(n))
assert d < 0.9408, f"Density should be less than 0.9408 but was {d}."
print(d) # 0.7715984980953817
为了节省时间这里直接逆序,很快,几分钟就出来了
from tqdm import tqdm
a=[65651991706497, 247831871690373, 120247087605020, 236854536567393, 38795708921144, 256334857906663, 120089773523233, 165349388120302, 123968326805899, 79638234559694, 259559389823590, 256776519514651, 107733244474073, 216508566448440, 39327578905012, 118682486932022, 263357223061004, 132872609024098, 44605761726563, 24908360451602, 237906955893793, 204469770496199, 7055254513808, 221802659519968, 169686619990988, 23128789035141, 208847144870760, 272339624469135, 269511404473473, 112830627321371, 73203551744776, 42843503010671, 118193938825623, 49625220390324, 230439888723036, 241486656550572, 107149406378865, 233503862264755, 269502011971514, 181805192674559, 152612003195556, 184127512098087, 165959151027513, 188723045133473, 241615906682300, 216101484550038, 81190147709444, 124498742419309]
re=4051501228761632
A = a[12:]
bits=36
def ju(j):for i in j:if abs(i)!=1:return 0return 1
for i in tqdm(range(2^12,1,-1)):temp=[int(j) for j in bin(i)[2:].zfill(12)]t1,t2=temp[:6],temp[6:12]if sum(t1)!=3 or sum(t2)!=3:continuerr = sum([i*j for i,j in zip(temp,a[:12])])new_re = re - rrM=Matrix(ZZ,bits+1)for i in range(bits):M[i,i]=2M[i,-1]=A[i]for i in range(bits):M[-1,i]=1M[-1,-1]=new_reres=M.LLL()if ju(res[0][:-1]):print('find')print(temp)print(res[0])break

CB ezDHKE
这题很常见也很简单就不说了
CB curve
CB cipher
这两题等有时间再继续复现吧
学习到了爆破+背包格
相关文章:

DASCTF-CBCTF-2023 Crypto部分复现
文章目录 EzRSACB backpack 这次比赛没打,记错时间了,看了一下,如果去做的话大概也只能做出那两道简单的题,还是太菜啦 EzRSA 题目描述: from Crypto.Util.number import * import random from gmpy2 import * from …...

为什么要做字节对齐 alignment?
下面这段 C 代码的输出是什么?定义的 Type 占用的字节数(下面简称为字节数)是多少呢? #include <iostream>struct Type {char a;int b; };int main(void) {std::cout << sizeof(Type) << \n; }经过编译运行&am…...
(零基础学习)Neo4j+Spring boot 自行定义属性
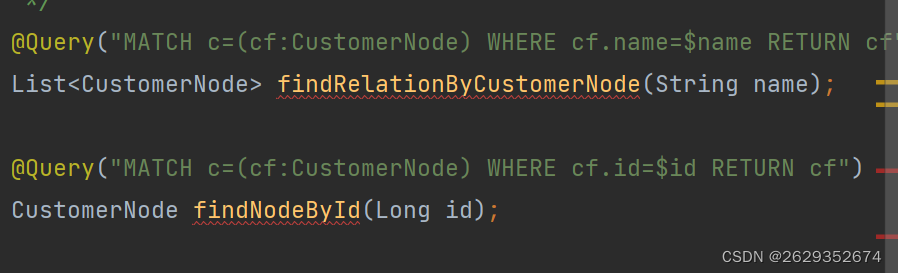
前置知识 1.Neo4j :属性 节点和关系都可以设置自己的属性。 属性是由Key-Value键值对组成,键名是字符串。属性值是要么是原始值,要么是原始值类型的一个数组。比如String,int和iint[]都是合法的。 注意 null不是一个合法的属性值。 Nulls能…...

【JavaEE】Java的文件IO
文件IO操作 Linux 下的文件操作讲解Java中的文件操作 -- 对文件的增删改查Java中对文件内容的操作 -- 读写操作使用案例 Linux 下的文件操作讲解 在我的Linux栏目下有, 如有需要, 点击下面进行跳转: 内存级文件系统语言级别的文教操作磁盘文件 Java中的文件操作 – 对文件的…...

域名解析与记录
域名解析是将域名转换为IP的过程,使得人们能够直接通过域名访问网站,而不用记繁琐的IP地址信息。而在域名解析中,CNAME记录和A记录是两个不同的记录类型。 A记录(Address Record,地址记录)是指将一个域名解…...

Android 13.0 第三方无源码apk授予QUERY_ALL_PACKAGES等其他权限的方法
1.概述 在13.0的系统产品中,对于内置第三方低版本app时,会有某些权限的冲突,导致在启动app时,崩溃掉,在查询相关日志发现是报权限的问题,所以就需要在安装解析app的时候,授予权限 2.第三方无源码apk授予QUERY_ALL_PACKAGES等其他权限的方法的核心类 /frameworks/base…...

【CSS】gird 网格
网格(Grid)是一种基于列数的布局系统,它可以帮助开发者创建具有水平和垂直分隔的页面布局。在CSS中,Grid是一种非常强大的布局工具,可以轻松地创建复杂的布局结构。Grid的主要属性包括: grid-template-col…...
(未完待续)【Netty专题】Netty实战与核心组件详解
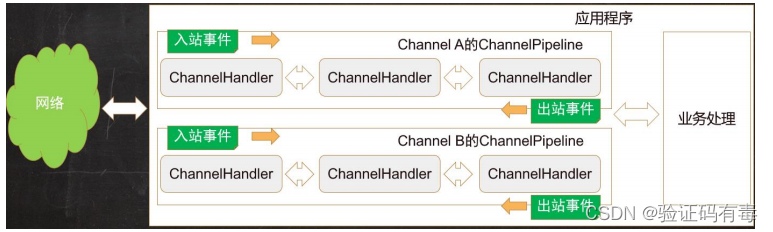
目录 前言阅读对象阅读导航前置知识课程内容一、Netty简介1.1 Netty是什么1.2 Netty有什么优势 二、第一个Netty程序2.1 Netty简单使用示例2.2 代码解读2.3 Netty的特性2.3.1 Netty的事件 2.4 Netty线程模型 三、Netty核心组件详解(未完待续)3.1 EventLo…...
“第四十五天” 数据结构基本概念
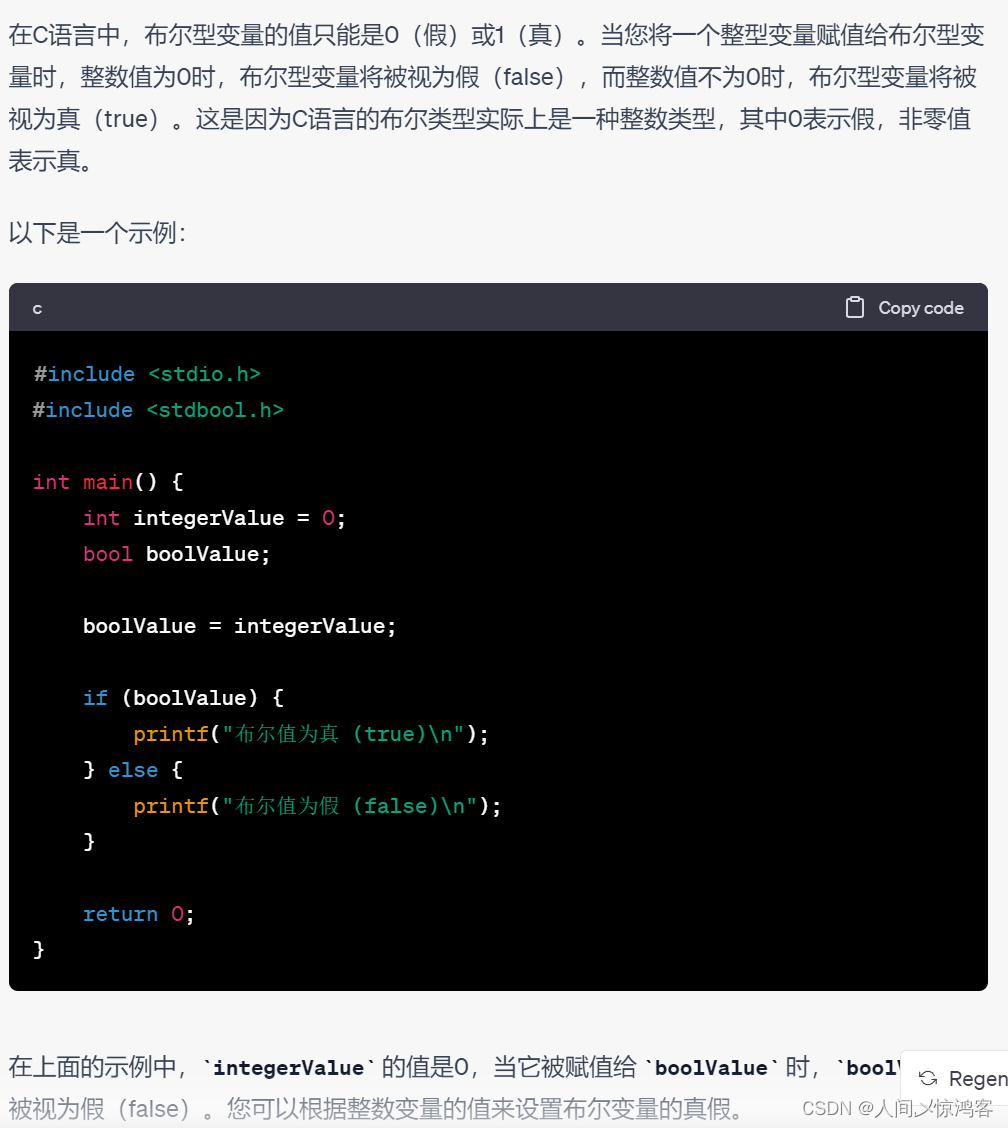
目前看的有关数据结构的课,估计这周就看完了,但感觉差很多,还是和c一样,这样过一下吧。但可能比较急,目前是打算争取寒假回家之前把四大件都先大致过一遍。 数据结构里面有很多新的定义和概念,学到现在&am…...
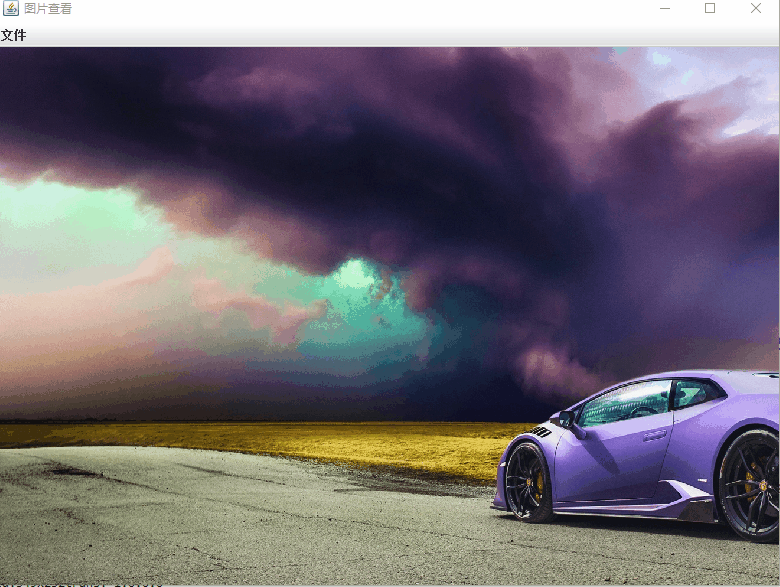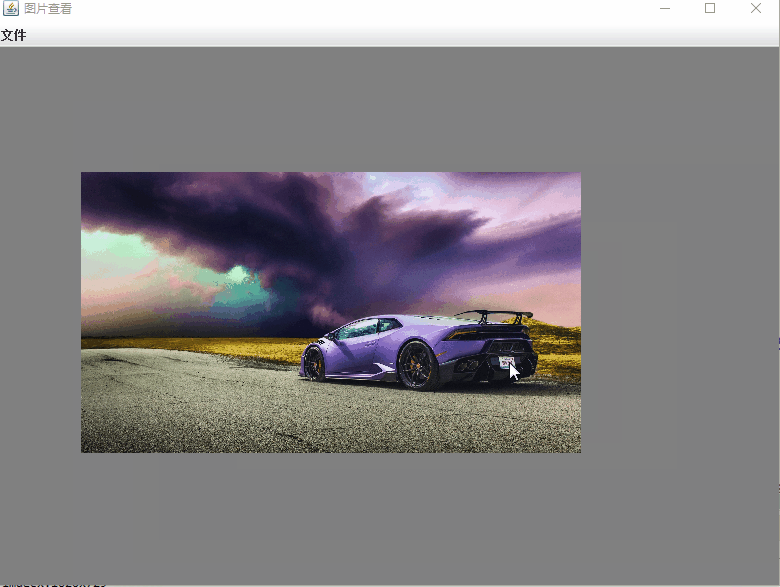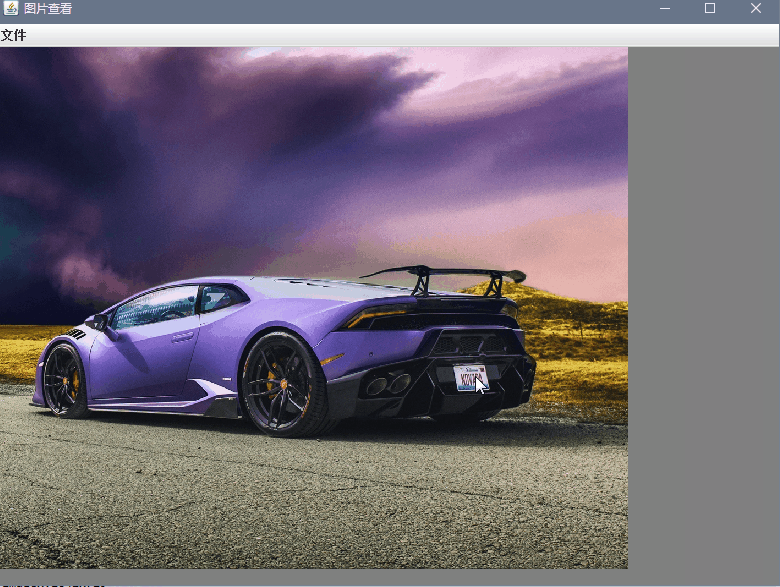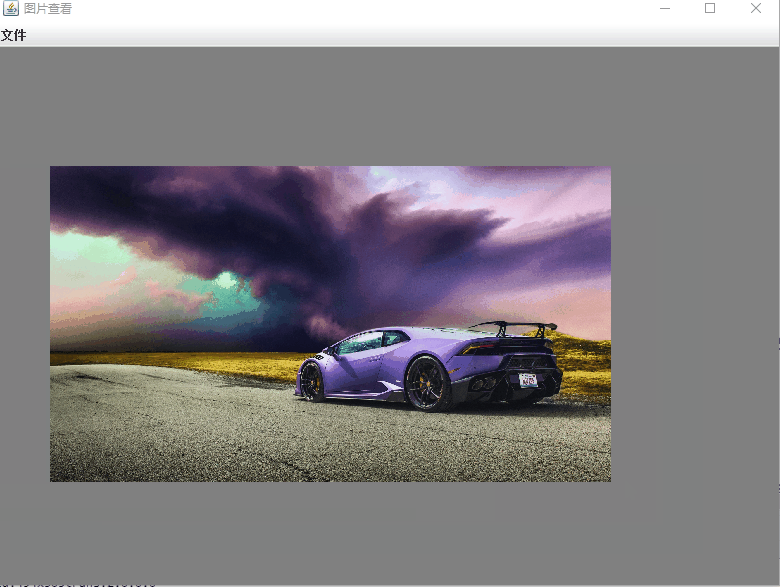
《java 桌面软件开发》swing 以鼠标为中心放大缩小移动图片
swing 使用Graphic2D 绘制图片,要实现对图片进行缩放和自由拖动。 1.以鼠标所在的位置为中心,滚轮控制缩放 2.缩放后再支持鼠标拖动。 基本原理: 利用scale() 函数。进行缩放。但是要注意的地方是,如果是在 public void paintCom…...

浅析人脸活体检测技术的功能及几种分类
在日常生活工作中,出现了人脸验证、人脸支付、人脸乘梯、人脸门禁等等常见的应用场景。这说明人脸识别技术已经在门禁安防、金融行业、教育医疗等领域被广泛地应用,人脸识别技术的高速发展与应用同时也出现不少质疑。其中之一就是人脸识别很容易被照片、…...

【Java基础面试三十五】、谈谈你对面向接口编程的理解
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:谈谈你对面向接口编程的…...

利用TreeMap来达成离散化的目的
假如有一些奶牛,他们有种类的区别,我们设黑色奶牛的id为1000010000,白色为1,诸如此类以此类推还有红色等各种颜色,接下来给你一群奶牛的颜色id让你统计每种颜色的奶牛有几头。 如过我们使用数组显然1000010000会爆空间…...

PG14安装_rpm方式
一、前期准备 发现生产环境有用rpm安装,故整理安装rpm安装步骤,目的是准备walminer恢复数据用的环境 二、安装包下载 https://download.postgresql.org/pub/repos/yum/ 含多个版本 https://download.postgresql.org/pub/repos/yum/14/redhat/rhel-7-x…...

水管安装过滤器笔记
文章目录 方案准备工具剪管钳热熔器软管接头及单向阀扳手 操作过程花洒 搬家后,水质不行,洗脸掉皮,洗头以前不掉头皮屑的,居然也掉头皮屑。有必要简单过滤下了。 水质情况,并不是脏脏的的那种水,看上去还比…...

【Objective-C】浅析Block及其捕获机制
目录 Block的基本使用Block的声明Block的实现Block的调用 Block作为形参使用Block作为属性使用给Block起别名Block的copy Block的捕获机制auto类型的局部变量__block浅析static类型的局部变量全局变量 其他问题 Block的基本使用 什么是Block? Block (块…...
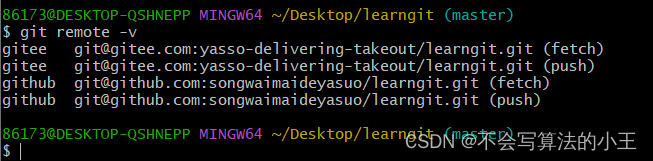
GitHub和Gitee的区别以及具体使用
文章目录 GitHub和GiteeGitHub和Gitee区别GitHub的使用Gitee的使用 GitHub和Gitee GitHub和Gitee区别 速度不同:GitHub位于美国,而Gitee位于中国。这意味着在中国使用Gitee可能会有更快的访问速度和更好的稳定性。如果我们希望体验Git飞一般的速度&…...

使用Redis实现分布式锁解决商品超卖问题(接上篇文章)
1. RedLock(红锁)简介 RedLock是一种用于分布式系统的锁定算法,旨在提供分布式锁的高可用性和分布式容错性。它是由Redis的创建者Salvatore Sanfilippo提出的,用于克服Redis单实例的单点故障问题。RedLock的目标是确保在多个Redis…...
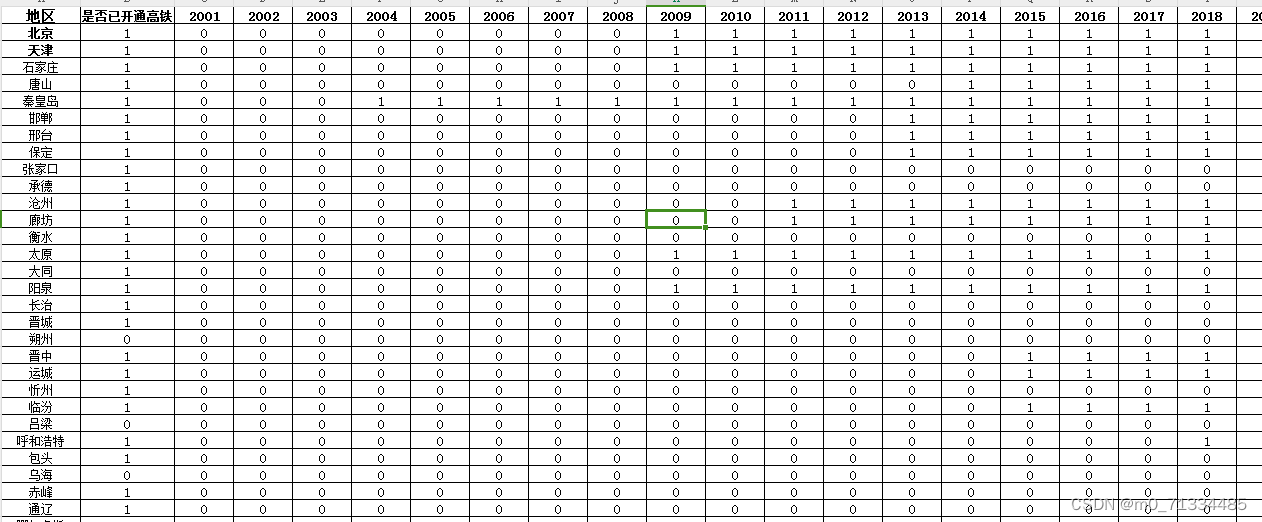
2001-2022年全国290+个地级市高铁开通数据
2001-2022年全国290个地级市高铁开通数据 1、时间:2001-2022年 2、范围:298地级市(293地级市数(其中莱芜市2019年撤市设区)4直辖市数 ) 3、来源:国家铁路局、铁路客货运输专刊及相关统计 国…...

【Java 进阶篇】深入浅出:Bootstrap 轮播图
在现代网页设计中,轮播图是一个常见的元素。它们可以用于展示图片、广告、新闻、产品或任何您希望吸引用户注意力的内容。要实现一个轮播图,您通常需要一些复杂的HTML、CSS和JavaScript代码,这对于初学者来说可能会感到困难。但幸运的是&…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
