使用Redis实现分布式锁解决商品超卖问题(接上篇文章)
1. RedLock(红锁)简介

RedLock是一种用于分布式系统的锁定算法,旨在提供分布式锁的高可用性和分布式容错性。它是由Redis的创建者Salvatore Sanfilippo提出的,用于克服Redis单实例的单点故障问题。RedLock的目标是确保在多个Redis实例上获取锁时,锁定操作在大多数实例上都成功。
RedLock的基本思想是,获取分布式锁需要在多个Redis实例上获取锁,至少需要在N/2 + 1个Redis实例上成功获取锁,其中N表示Redis实例的总数。这样做是为了保证锁在大多数实例上是可用的。
RedLock的步骤如下:
-
获取当前时间戳。
-
在每个Redis实例上尝试获取锁,使用相同的锁名称、唯一标识符和超时时间。
-
统计成功获取锁的实例数量。
-
如果成功获取锁的实例数量大于等于N/2 + 1,则认为锁获取成功。
-
否则,在成功获取锁的实例上释放锁,确保锁不会被占用。
RedLock的优点是它提供了高可用性,即使其中一个Redis实例出现问题,其他实例仍可以提供服务。然而,需要注意的是,RedLock仍然依赖于Redis,如果所有Redis实例都无法正常工作,那么RedLock也无法正常运行。
总之,RedLock是一种用于提供分布式锁的算法,它充分考虑了高可用性和分布式容错性,适用于需要可靠锁定机制的分布式系统。
2. Redisson简介
Redisson是一个开源的Java框架,它为Redis提供了一组分布式Java对象和服务,使得在Java应用程序中使用Redis变得更加容易。Redisson的目标是简化分布式系统的开发,提供易于使用的API和丰富的功能集合,以满足不同分布式应用的需求。
Redisson提供了一些常见的分布式数据结构和服务,如分布式锁、分布式集合、分布式Map、分布式队列、分布式消息发布/订阅等,这些功能可以方便地在分布式应用中使用。Redisson还提供了一种流畅的API,使开发人员可以更容易地与Redis进行交互,同时还提供了许多性能优化和线程安全的功能。
使用Redisson,开发人员可以更容易地构建分布式系统,从而充分利用Redis的强大功能,提高应用程序的性能和可伸缩性。这个框架已经被广泛用于构建各种分布式应用,如缓存、任务队列、分布式锁和会话管理等。
3. 解决方案
3.1 版本12
使用基于红锁的Redission客户端实现分布式加锁多台Redis实例:
-
添加Redisson依赖:首先,确保你的项目中引入了Redisson依赖。
-
初始化Redisson:创建Redisson的客户端并配置多个Redis实例的信息。
Config config = new Config();
config.useClusterServers().addNodeAddress("redis://server1:6379").addNodeAddress("redis://server2:6379").addNodeAddress("redis://server3:6379").addNodeAddress("redis://server4:6379").addNodeAddress("redis://server5:6379");RedissonClient redisson = Redisson.create(config);- 获取锁并执行业务逻辑:
RLock lock = redisson.getLock("order_lock");try {boolean isLocked = lock.tryLock(1, 10, TimeUnit.SECONDS); // 尝试获取锁,等待1秒,锁定10秒if (isLocked) {String retMessage = "";try{// 1.查询库存String resultFromRedis = stringRedisTemplate.opsForValue().get(key);// 判断库存是否足够Integer num=resultFromRedis == null?0:Integer.parseInt(resultFromRedis);if(num-count > 0){stringRedisTemplate.opsForValue().set(key,String.valueOf(--num));retMessage = "成功卖出"+count+"件商品"+"服务端口号:"+serverPort;System.out.println(retMessage+"当前商品剩余:"+(num+1-count)+"件。");// 模拟长业务try {TimeUnit.SECONDS.sleep(200);} catch (InterruptedException e) {e.printStackTrace();}}else{retMessage="商品已售罄!非常抱歉!";System.err.println(retMessage);}}} else {// 获取锁失败,可以处理一些逻辑,如返回错误信息}
} finally {lock.unlock();
}- 关闭Redisson客户端:在应用程序关闭时,记得关闭Redisson客户端。
redisson.shutdown();这个示例中,我们使用了Redisson的RLock来获取分布式锁,确保只有一个线程能够执行扣减库存的逻辑。如果你的应用需要高可用性和分布式容错性,你可以使用RedLock算法,它需要至少在N/2 + 1个Redis实例上获取锁,以保证锁的可用性。
相关文章:

使用Redis实现分布式锁解决商品超卖问题(接上篇文章)
1. RedLock(红锁)简介 RedLock是一种用于分布式系统的锁定算法,旨在提供分布式锁的高可用性和分布式容错性。它是由Redis的创建者Salvatore Sanfilippo提出的,用于克服Redis单实例的单点故障问题。RedLock的目标是确保在多个Redis…...
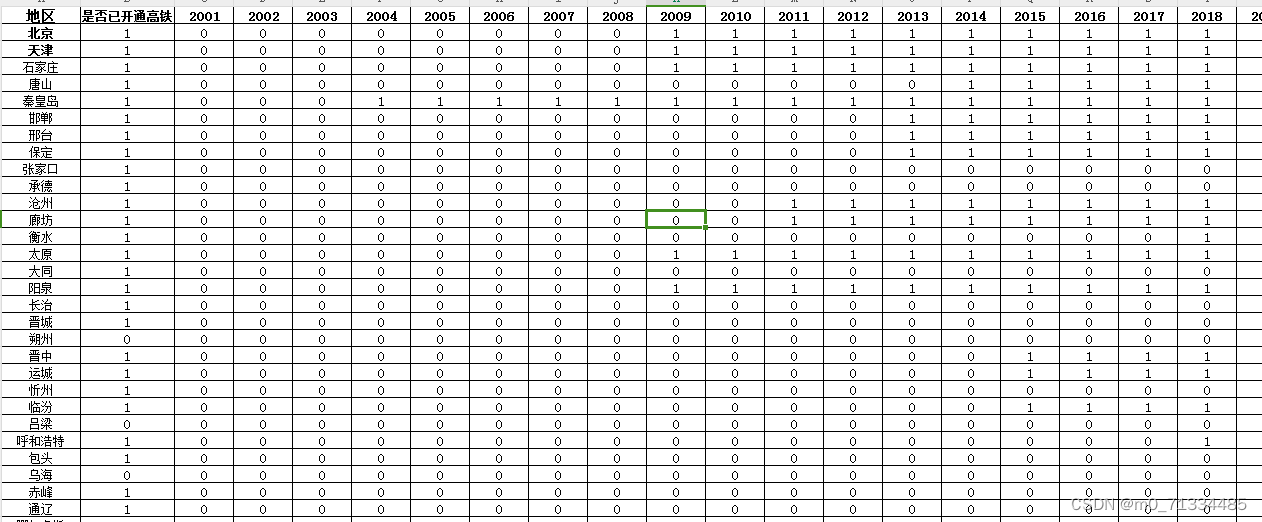
2001-2022年全国290+个地级市高铁开通数据
2001-2022年全国290个地级市高铁开通数据 1、时间:2001-2022年 2、范围:298地级市(293地级市数(其中莱芜市2019年撤市设区)4直辖市数 ) 3、来源:国家铁路局、铁路客货运输专刊及相关统计 国…...

【Java 进阶篇】深入浅出:Bootstrap 轮播图
在现代网页设计中,轮播图是一个常见的元素。它们可以用于展示图片、广告、新闻、产品或任何您希望吸引用户注意力的内容。要实现一个轮播图,您通常需要一些复杂的HTML、CSS和JavaScript代码,这对于初学者来说可能会感到困难。但幸运的是&…...

75. 颜色分类
75. 颜色分类 双指针——快慢指针 class Solution {public void sortColors(int[] nums) {int n nums.length;int p0 0;for(int i 0; i < n; i){if(nums[i] 0){swap(nums, p0, i);p0;}}int p1 p0;for(int i p0; i < n; i){if(nums[i] 1){swap(nums, p1, i);p1;}…...

网络协议--IP:网际协议
3.1 引言 IP是TCP/IP协议族中最为核心的协议。所有的TCP、UDP、ICMP及IGMP数据都以IP数据报格式传输(见图1-4)。许多刚开始接触TCP/IP的人对IP提供不可靠、无连接的数据报传送服务感到很奇怪。 不可靠(unreliable)的意思是它不能…...
)
【考研数学】线性代数第六章 —— 二次型(3,正定矩阵与正定二次型)
文章目录 一、基本概念1.1 引例1.2 正定二次型概念 二、正定二次型的判别写在最后 一、基本概念 1.1 引例 (1)二次型 f ( x 1 , x 2 , x 3 ) x 1 2 3 x 2 2 2 x 3 2 X T A X f(x_1,x_2,x_3)x_1^23x_2^22x_3^2\pmb{X^TAX} f(x1,x2,x3)x123…...

【Java 进阶篇】手把手教你创建 Bootstrap 旅游网站
随着互联网的普及,旅游行业在全球范围内迅速发展。人们通过网络规划、预订和分享他们的旅行经历。因此,拥有一个令人印象深刻的旅游网站对于吸引游客和提供有用信息至关重要。在本篇博客中,我们将手把手教您如何创建一个令人兴奋的旅游网站&a…...
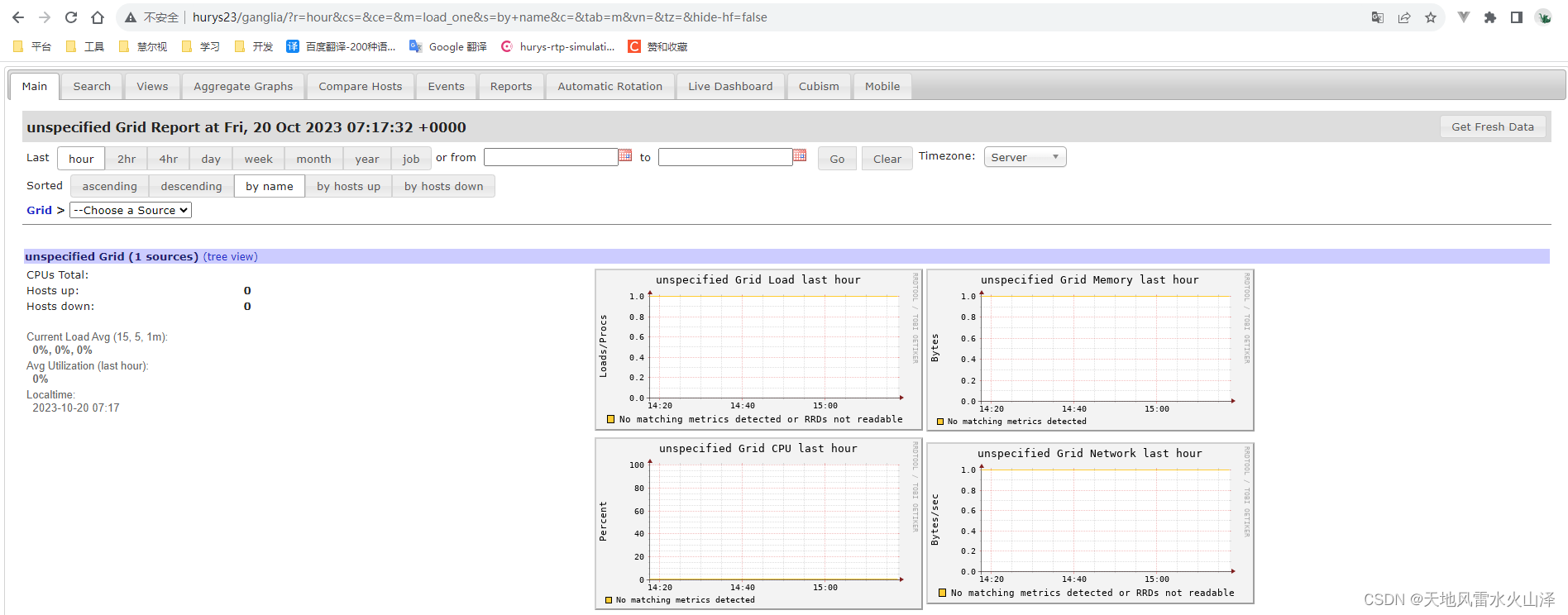
一百九十二、Flume——Flume数据流监控工具Ganglia单机版安装
一、目的 在安装好Flume之后,需要用一个工具可以对Flume数据传输进行实时监控,这就是Ganglia 二、Ganglia介绍 Ganglia 由 gmond、gmetad 和 gweb 三部分组成。 (一)第一部分——gmond gmond(Ganglia Monitoring Da…...

光学知识整理-偏振光
偏振光 目录基础概念基础概念的补充平面偏振光(线偏振光)部分偏振光圆偏振光椭圆偏振光菲涅耳公式相位关系 反射折射所引起的偏振态的改变斯托克斯倒逆关系重要参数 目录 基础概念 光是横波:光是电磁波,其电场分量(电场强度)E、磁场分量(磁…...

CUDA纹理内存tex1D/tex2D/tex3D函数
CUDA的tex1D是用于从一维纹理中读取数据的函数。纹理是一种特殊的内存区域,可以用来存储图像、视频或其他数据。tex1D函数可以用于从纹理中读取数据,并将其传递给CUDA程序。 tex1D函数的语法如下: float tex1D(sampler_t sampler, float te…...

【Java基础面试三十八】、请介绍Java的异常接口
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:请介绍Java的异常接口 …...

LabVIEW中的数据通信方法
LabVIEW中的数据通信方法 LabVIEW中包含多种数据通信方法,不同的方法适用于不同的场景。应该先了解概述,确保在应用程序中使用正确的数据通信方法。 数据通信类型: 数据流元素 缓冲接口 变量接口 应用场景: 在多数程序框图对…...

记调试SMBUS的心得
为什么电池电压读的不对 仔细一看是I2C读取数据的时候少了一个CLK I2C是非常严密的 读数据之后,发送 ACK,让从机准备数据 发送NACK,告诉从机别准备了 ACK和NACK的区别是啥,告诉你,就是NACK先拉高SDA,再…...

【C++】:类和对象(中)之拷贝构造函数+赋值运算符重载
拷贝构造函数 概念 在现实生活中,可能存在一个与你一样的自己,我们称其为双胞胎 那在创建对象时,可否创建一个与已存在对象一某一样的新对象呢? 拷贝构造函数:只有单个形参,该形参是对本类类型对象的引用…...
C++迭代器失效
在STL中,有些操作会导致迭代器失效,即之前获取的迭代器无法再安全地使用。这是因为这些操作可能会改变容器的结构,例如插入、删除元素等。 具体来说,以下情况下迭代器会失效: 1. 当插入或删除元素导致容器中的内存重新…...
--iotauth - IoT鉴权库, 用于生成各种云平台的参数)
LuatOS-SOC接口文档(air780E)--iotauth - IoT鉴权库, 用于生成各种云平台的参数
iotauth.aliyun(product_key, device_name,device_secret,method,cur_timestamp) 阿里云物联网平台三元组生成 参数 传入值类型 解释 string product_key string device_name string device_secret string method 加密方式,”hmacmd5” “hmacsha1” “hmacsha256”…...
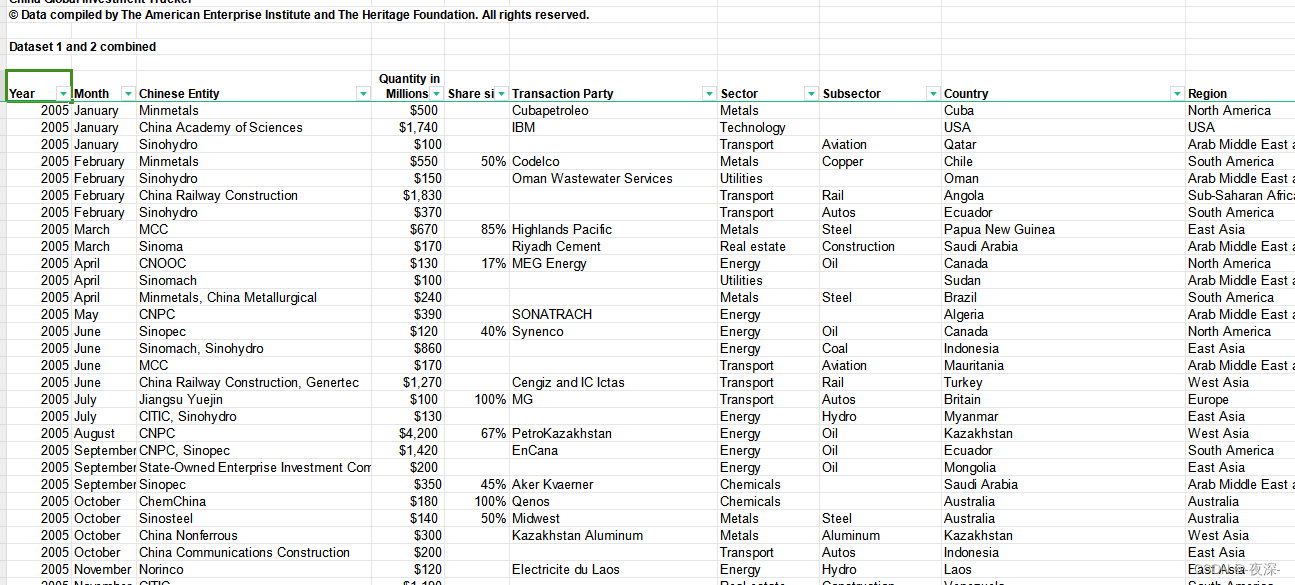
2005.6-2018.6月中国企业OFDI微观数据
2005.6-2018.6月中国企业OFDI微观数据 1、时间:2005.6-2018.6 2、范围:公司 3、指标:Year、Month、Chinese Entity、 Quantity in Millions 、Share size、Transaction Party、Sector、Subsector、Country、Region、BRI 4、数据解释&…...

Spring和SpringBoot学习
Spring和SpringBoot学习 Spring中常用注解及其作用 Spring中常用注解及其作用 SpringBoot注解扫描范围 SpringBoot | ComponentScan()注解默认扫描包范围分析 spring boot的包扫描范围 springBoot的自动扫描包范围 SpringBoot中new对象不能自动注入对象 SpringBoot中new对…...
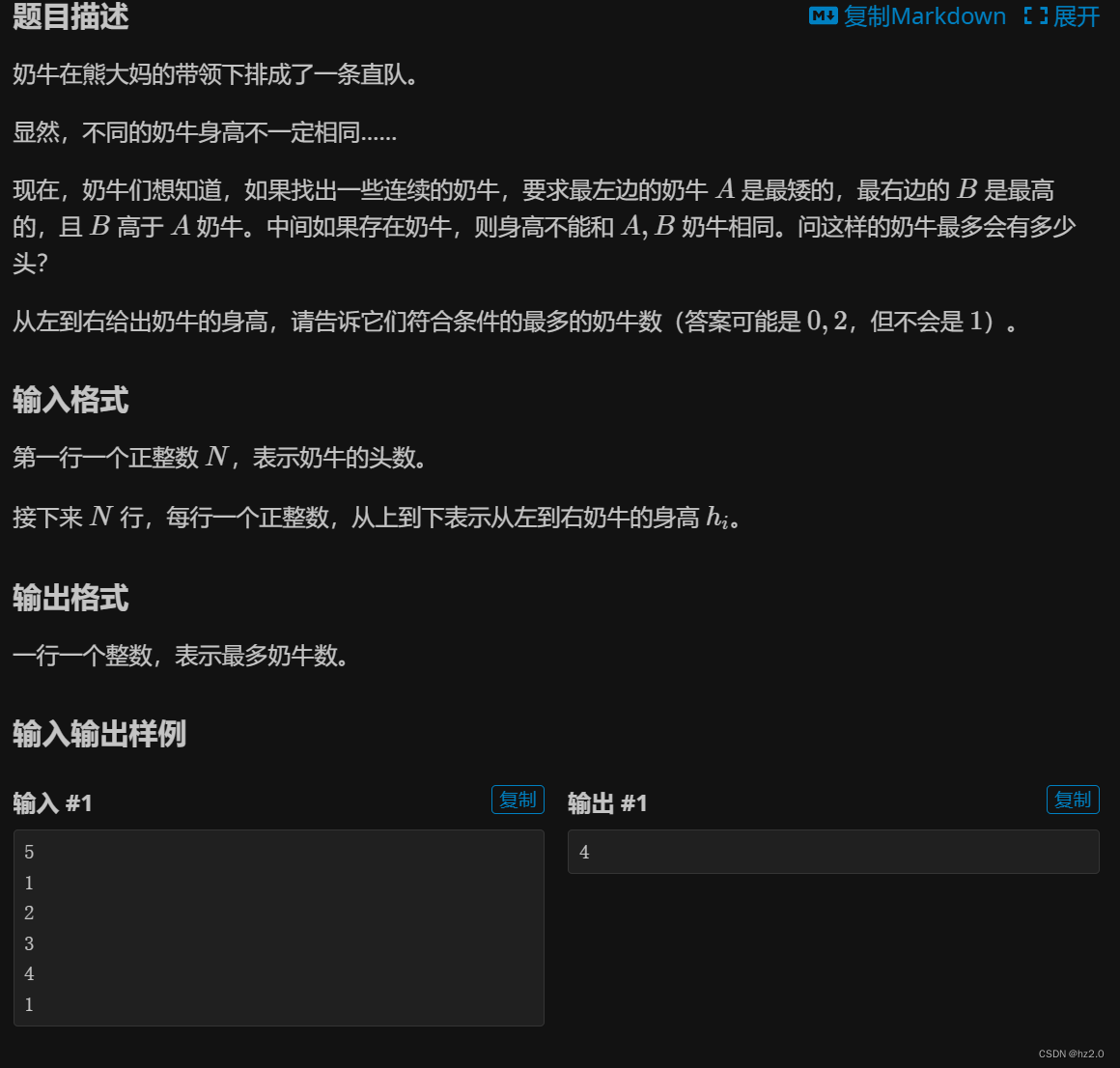
P6510 奶牛排队
题目 P6510 奶牛排队 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 思路 1.dp求最大。(dp即前后关联)arr[]用于存储输入的数据,brr[i]用于存储以第i头牛为右端点的队列最大值。 2.数组空间不够大,我们可以自己开辟对空间&…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...