当前位置： 首页 > news >正文

【试题039】 多个逻辑或例题

news 2026/2/8 14:50:52
  1. 题目：设int n;,执行表达式(n=0)||(n=1)||(n=2)||(n=3)后,n的值是？
  2. 代码+分析：
  //设int n; , 执行表达式(n = 0) || (n = 1) ||(n = 2) ||(n = 3)后, n的值是?int n;printf("n=%d\n", (n = 0) || (n = 1) || (n = 2) || (n = 3));//分析：先考虑逻辑或是否短路，再看运算符优先级// 首先赋值n=0,不短路，继续n=1,逻辑或是有一个为真即为真，后边不用再执行//此时n=1,表达式结果也是1
}

3.截图：

相关文章：

【试题039】 多个逻辑或例题

题目：设int n;,执行表达式(n0)||(n1)||(n2)||(n3)后,n的值是？代码分析： //设int n; , 执行表达式(n 0) || (n 1) ||(n 2) ||(n 3)后, n的值是?int n;printf("n%d\n", (n 0) || (n 1) || (n 2) || (n 3));//分析&#xff1…...

编程日记 2023/10/23 3:03:49

打卡go学习第一天

8.1 下面展示一些 代码。 package mainimport ("fmt""net""os""time" )type Clock struct {Name stringAddr string ｝ func main() {clocks : []Clock{{Name: "New York", Addr: "localhost:8000"…...

编程日记 2023/10/23 3:02:48

julia 笔记： 流程控制

1 复合表达式 用一个表达式有序地计算若干子表达式&#xff0c;并返回最后一个子表达式的值 1.1 begin代码块 z beginx 1y 2x yend z #3begin x 1; y 2; x y end #3 1.2 ;链 (x 1; y 2; x y) #3(x 1; y 2; x y) 3 2 条件表达式 x1 y2if x < yprintln(&q…...

编程日记 2023/10/23 3:01:47

【c++】 跟webrtc学周期性任务：tgcalls 5 网络超时检查

tgcalls 网络超时检查 G:\CDN\P2P-DEV\tdesktop-offical\Telegram\ThirdParty\tgcalls\tgcalls\NetworkManager.cppPostDelayedTask 使用的是rtc thread 方法 PostDelayedTask ：G:\CDN\P2P-DEV\Libraries\tg_owt\src\rtc_base\thread.htemplate <class Closure,typename st…...

编程日记 2023/10/23 2:59:45

面试算法33：变位词组

题目 给定一组单词&#xff0c;请将它们按照变位词分组。例如&#xff0c;输入一组单词[“eat”&#xff0c;“tea”&#xff0c;“tan”&#xff0c;“ate”&#xff0c;“nat”&#xff0c;“bat”]&#xff0c;这组单词可以分成3组&#xff0c;分别是[“eat”&#xff0c;“…...

编程日记 2023/10/23 2:58:44

【C语言】每日一题（旋转数组）

旋转数组&#xff0c;链接奉上 目录 方法:创建额外的数组&#xff1a;整体思路&#xff1a;代码实现&#xff1a; 数组反转&#xff1a;整体思路&#xff1a;代码实现&#xff1a;小插曲&#xff1a; 方法: 创建额外的数组&#xff1a; 整体思路&#xff1a; 创建一个额外的…...

编程日记 2023/10/23 2:56:41

系统架构师考试科目一：综合知识

某软件公司欲开发一个 Windows 平台上的公告板系统。在明确用户需求后&#xff0c;该公司的 架构师决定采用 Command 模式实现该系统的界面显示部分&#xff0c;并设计 UML 类图如下 图所示。图中与 Command 模式中的 Invoker 角色相对应的类是( ) &#xff0c;与 ConcreteComm…...

编程日记 2023/10/23 2:55:40

面向对象与面向过程讲解

目录 简介 面向过程编程&#xff08;Procedural Programming&#xff09; 什么是面向过程编程&#xff1f; 特点&#xff1a; 面向对象编程&#xff08;Object-Oriented Programming&#xff09; 什么是面向对象编程&#xff1f; 特点&#xff1a; 面向对象 vs. 面向过程…...

编程日记 2023/10/23 2:54:40

【SA8295P 源码分析 (四)】23 - QNX Ethernet MAC 驱动 之 emac1_config.conf 配置文件解析

【SA8295P 源码分析】23 - QNX Ethernet MAC 驱动 之 emac1_config.conf 配置文件解析 系列文章汇总见：《【SA8295P 源码分析 (四)】网络模块 文章链接汇总 - 持续更新中》 本文链接：《【SA8295P 源码分析 (四)】23 - QNX Ethernet MAC 驱动 之 emac1_config.conf 配置文件解…...

编程日记 2023/10/23 2:53:39

Python【list列表去重】

目录 要求&#xff1a; 将list中的重复数据去重&#xff0c;至少使用两种方案 方案一&#xff1a; 方案二&#xff1a; 要求&#xff1a; 将list中的重复数据去重&#xff0c;至少使用两种方案 方案一&#xff1a; 使用set &#xff0c;可以将list转换为set&#xff0…...

编程日记 2023/10/23 2:51:36

Leetcode——字符

520. 检测大写字母 class Solution { public:bool detectCapitalUse(string word) {int big 0, small 0, len word.length();for (int i 0; i < len; i) {if (word[i] > 65 && word[i] < 90) {big;}else {small;}}if (big len || small len) {return tr…...

编程日记 2023/10/23 2:50:35

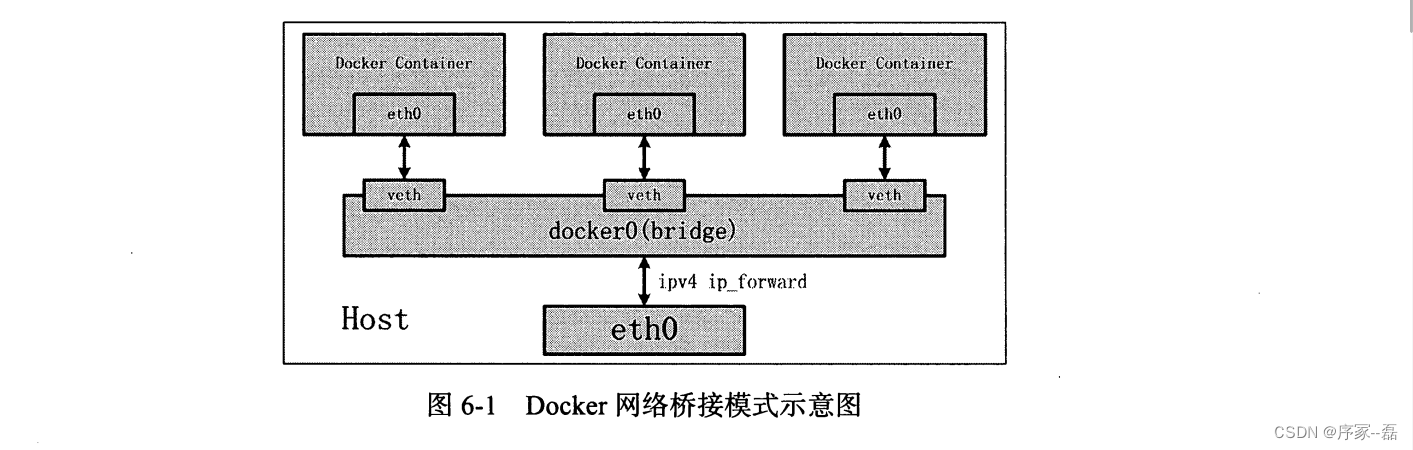
深入解析docker内核网桥

今天做虚拟桌面&#xff0c;朋友问我&#xff0c;为什么vnc 连接另一个docker 容器一直超时&#xff0c;原因是在docker 启动的时候没有组网&#xff0c;那么接下来我就要解析下docker的内核网络。 我们思考几个问题&#xff0c;带你了解linux 中docker 网络实现的基本原理。 文…...

编程日记 2023/10/23 2:49:32

ubuntu18.04服务器双网口配置上外网

记录一下配置服务器过程&#xff0c;本以为简单&#xff0c;结果整了一天。 服务器有2个网口&#xff0c;网口2是用来上外网的&#xff0c;原来用的01-netcfg.yaml进行ip地址设置&#xff0c;主要就用2条命令&#xff1a; vi /etc/netplan/01-netcfg.yaml &#xff08;打开后…...

编程日记 2023/10/23 2:48:31

【安全体系架构】——防御深度架构

防御深度架构&#xff1a; 防御深度架构是一种多层次的安全模型&#xff0c;旨在通过在网络和系统的各个层次上部署多个安全措施&#xff0c;以抵御不同类型的威胁和攻击。这个模型承认单一的安全措施可能无法全面防御所有潜在威胁&#xff0c;因此采用了多层次的安全防御策略…...

编程日记 2023/10/23 2:46:28

Opencv之RANSAC算法用于直线拟合及特征点集匹配详解

Opencv之RANSAC算法用于直线拟合及特征点集匹配详解 讲述Ransac拟合与最小二乘在曲线拟合上的优缺点 讲述在进行特征点匹配时&#xff0c;最近邻匹配与Ransac匹配的不同之处 另外&#xff0c;Ransac也被用于椭圆拟合、变换矩阵求解等 1. 直线拟合 1.1 原理 RANSAC(RANdom …...

编程日记 2023/10/23 2:45:26

Jenkins环境部署与任务构建

一、CI/CD 1、CI/CD 概念&#xff1a; CI/CD 是一种软件开发和交付方法&#xff0c;旨在加速应用程序的开发、测试和部署过程&#xff0c;以提高软件交付的质量和效率。 (1) 持续集成 (CI Continuous Integration): 持续集成是开发团队频繁集成其代码更改的过程。开发者将其…...

编程日记 2023/10/23 2:44:26

ES6 Class和Class继承

1.class的基本语法 class可以理解为是一个语法糖&#xff0c;将js只能通过构造函数创建实例的方法进行了补充 构造函数&#xff1a; function Person ({ name, age18 }) {this.name namethis.age age } new Person({name: 张三}) Class类&#xff1a; class Person {con…...

编程日记 2023/10/23 2:42:22

C++11 packaged_task

std::packaged_task 把一个方法打包成一个task扔到线程中执行&#xff0c;然后通过packaged_task中的furture等待执行结果。 void test_promise() {std::packaged_task <int()> task([]()->int {std::cout << "packaged_task begin \n" << std…...

编程日记 2023/10/23 2:40:20

delete、drop、truncate三兄弟

比较方面/具体命令deletetruncatedrop删除范围逐行删除&#xff08;记录行&#xff09;逐页删除&#xff08;数据页&#xff09;整张表&#xff08;数据表结构&#xff09;所属范畴数据操作语言&#xff08;DML&#xff09;数据定义语言&#xff08;DDL&#xff09;数据定义语言…...

编程日记 2023/10/23 2:39:19

C/C++运算优先级

文章目录 前言1.运算优先级表2.举例说明&#xff1a;总结 前言 最近复习C基础知识的时候&#xff0c;发现对这部分还是有些模糊。常用的 - &#xff0c;括号等运算符对于它们的优先级还是比较明确的。但是涉及到移位运算&#xff0c;逻辑运算这种&#xff0c;再结合四则运算…...

编程日记 2023/10/23 2:36:17

spring：实例工厂方法获取bean

spring处理使用静态工厂方法获取bean实例&#xff0c;也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下&#xff1a; 定义实例工厂类&#xff08;Java代码&#xff09;&#xff0c;定义实例工厂&#xff08;xml&#xff09;&#xff0c;定义调用实例工厂&#xff…...

编程新知 2025/11/25 22:46:30

Spring Boot+Neo4j知识图谱实战：3步搭建智能关系网络！

一、引言 在数据驱动的背景下&#xff0c;知识图谱凭借其高效的信息组织能力&#xff0c;正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合&#xff0c;探讨知识图谱开发的实现细节&#xff0c;帮助读者掌握该技术栈在实际项目中的落地方法。 …...

编程新知 2025/9/17 21:39:04

什么？连接服务器也能可视化显示界面？：基于X11 Forwarding + CentOS + MobaXterm实战指南

文章目录 什么是X11？环境准备实战步骤1️⃣ 服务器端配置（CentOS）2️⃣ 客户端配置（MobaXterm）3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/55aefaea8a9f477e86d065227851fe3d.pn…...

编程新知 2025/10/2 17:12:14

LLMs 系列实操科普（1）

写在前面&#xff1a; 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容&#xff0c;原视频时长 ~130 分钟&#xff0c;以实操演示主流的一些 LLMs 的使用&#xff0c;由于涉及到实操&#xff0c;实际上并不适合以文字整理&#xff0c;但还是决定尽量整理一份笔…...

编程新知 2026/1/31 11:35:24

Python+ZeroMQ实战：智能车辆状态监控与模拟模式自动切换

目录 关键点 技术实现1 技术实现2 摘要&#xff1a; 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式&#xff08;自动驾驶、人工驾驶、远程驾驶、主动安全&#xff09;&#xff0c;并通过实时消息推送更新车…...

编程新知 2025/11/12 0:06:50

c++第七天 继承与派生2

这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分&#xff1a;派生类构造函数与析构函数 当创建一个派生类对象时&#xff0c;基类成员是如何初始化的&#xff1f; 1.当派生类对象创建的时候&#xff0c;基类成员的初始化顺序 …...

编程新知 2026/2/2 21:55:02

Elastic 获得 AWS 教育 ISV 合作伙伴资质，进一步增强教育解决方案产品组合

作者&#xff1a;来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布&#xff0c;Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明&#xff0c;Elastic 作为 …...

编程新知 2026/2/7 16:38:17

第八部分：阶段项目 6：构建 React 前端应用

现在&#xff0c;是时候将你学到的 React 基础知识付诸实践&#xff0c;构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段&#xff0c;你可以先使用模拟数据&#xff0c;或者如果你的后端 API&#xff08;阶段项目 5&#xff09;已经搭建好&#xff0c;可以直接连…...

编程新知 2025/9/21 1:58:01

AD学习（3）

1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分&#xff1a; &#xff08;1&#xff09;PCB焊盘&#xff1a;表层的铜 &#xff0c;top层的铜 &#xff08;2&#xff09;管脚序号&#xff1a;用来关联原理图中的管脚的序号&#xff0c;原理图的序号需要和PCB封装一一…...

编程新知 2026/2/8 10:47:16

Python常用模块：time、os、shutil与flask初探

一、Flask初探 & PyCharm终端配置 目的： 快速搭建小型Web服务器以提供数据。 工具： 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask： 建议： 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装，避免频繁切换。 PyCharm Terminal 配置建议： 打开 Py…...

编程新知 2026/2/7 9:52:39