数据结构与算法之[把数字翻译成字符串]动态规划
前言:最近在刷动态规划的算法题目,感觉这一类题目还是有一点难度的,但是不放弃也还是能学好的,今天给大家分享的是牛客网中的编程题目[把数字翻译成字符串],这是一道经典的面试题目,快手,字节跳动等大厂出国这道题目。题目有点绕,需要进行分类讨论最好配合画图工具进行理解,这样能更好理解这道题目。
一.题目

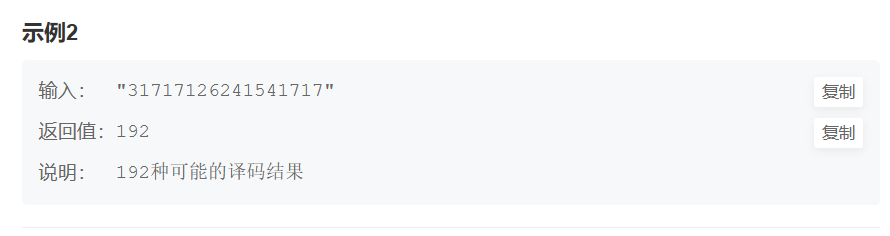
二.进一步剖析题目
1.关于动态规划思想
动态规划算法的基本思想是:将待求解的问题分解成若干个相互联系的子问题,先求解子问题,然后从这些子问题的解得到原问题的解;对于重复出现的子问题,只在第一次遇到的时候对它进行求解,并把答案保存起来,让以后再次遇到时直接引用答案,不必重新求解。动态规划算法将问题的解决方案视为一系列决策的结果。
2.分析题目
①分析题目:能够译码的数字不会大于26,即有效的译码范围为 [1,26]。
②确定状态:以数组 "12345" 为例,首先要明确两点:
依题意可知,数组中所有的数字都必须参与译码,比如数组 "1234" 的某一种译码方式为 “1,2,3,4",那么当数组尾再添加一个元素 "5" 时,刚才的译码方式就会变为 "1,2,3,4,5",即 "1,2,3,4" 和 "1,2,3,4,5" 是同一种译码方式。
由于所有数字都要参与译码,所以只要译码方式中存在个位数 "0",那么就都是无效的。
当新加入一个数字"5" 时,其除了可以单独作为一个数字参与译码外,也可以与其左边的数字组成数字组合后再参与译码,即 "45" ,然后此时有多少种译码方式就取决于剩余的数字 即 "123" 了,这和前面所说的是同一个道理,只是此时把 "4"和"5" 看作是一个整体,可以理解为:原本数组 "123" 存在某种译码方式为 "1,2,3",现在加入 "45",译码方式就变成了 "1,2,3,45"。
由于有效的译码范围为 [1,26],所以新加入的数字 "5" 只需要考虑与其左边的数字组成两位数组合,无需再考虑组成更大的组合了,比如三位数 "345" 等等。
数字组合必须是十位数,比如 "0"和"2" 组成的 "02" 也是不符合译码要求的。
理解了上面两点后,现在我们从数组 "12345" 的子串"1"开始分析,然后逐步往后添加元素,设数组 x 有 f(x) 种有效的译码方式:
当数组为 "1" 时,有以下译码方式:
①1
f("1")=1
接着加入数字"2",数组为 "12" 时,有以下译码方式:
①1,2
②12
f("12")=2
其中第①种是从 数组 "1" 的译码方式 演变过来的,就是在其基础上再加上单个数字 "2"。
接着加入数字"3",数组为 "123" 时,有以下译码方式:
①1,2,3
②12,3
③1,23
f("123")=3
其中第①、②种是从 数组 "12" 的译码方式 演变过来的,就是在其基础上再加上单个数字 "3";
而第③种是从 数组 "1" 的译码方式 演变过来的,就是在其基础上再加上数字组合 "23"。
接着加入数字"4",数组为 "1234" 时,有以下译码方式:
①1,2,3,4
②12,3,4
③1,23,4
④1,2,34
⑤12,34
其中第①、②、③种是从 数组 "123" 的译码方式 演变过来的,就是在其基础上再加上单个数字 "4";
而第④、⑤种是从 数组 "12" 的译码方式 演变过来的,就是在其基础上再加上数字组合 "34";
由于 "45" 不在有效译码的范围内,所以这两种译码方式会被抛弃掉。
f("1234")=3
可见,数组 "1234" 的译码方式 是由 数组 "123"的译码方式 和 数组 "12"的译码方式 组成的。
根据上面的分析,当数组继续扩张到 "12345" 时,那么其译码方式就为:
当新加入的数字 "5" 单独作为个位数参与译码时,此时的译码方式 就等同于 数组 "1234" 的译码方式,这组译码方式是有效的,因为个位数 "5" 在有效的译码范围内;
而 "5" 与其前一位数字组成十位数 "45" 时,此时的译码方式 就等同于 数组 "123" 的译码方式,而这组译码是否有效则取决于 "45" 是否在有效的译码范围内。
即 f("12345") = f("12345" - "5") + f("12345" - "45") = f("1234") + f("123") = 3+3 = 6,但是由于 "45" 不在有效的译码范围内,所以 f("123") 的结果不能算在内,所以最终结果应该为3。
可见,枚举到某位数字时,此时有多少种译码方式,可以由之前的译码方式相加得出,即当前的状态可以利用之前的状态,这是典型的动态规划。
③状态转移方程:f(x)=f(x-1)+f(x-2)(其中 x 表示数组长度,f(x) 表示有多少种有效的译码方式;是否加上 f(x-1) 取决于 nums[x] 是否在 [1,9] 内,即 nums[x] 需要满足不为0;是否加上 f(x-2) 则取决于 nums[i-1] 与 nums[i] 的数字组合是否在 [10,26] 内)
时间复杂度:O(N) ,需要遍历一次数组
空间复杂度:O(N) ,需要声明一个状态数组记录f(x)
3.C++代码
class Solution {public:int solve(string nums) {// write code hereif(nums[0]=='0')return 0;vector<int>dp(nums.size(),0);dp[0]=1;for(int i=1;i<dp.size();i++){if(nums[i]!='0'){if(nums[i-1]=='1'){dp[i]=dp[i-1]+(i-2>=0?dp[i-2]:1);continue;}if(nums[i-1]=='2'&&(nums[i]-'0'>0&&nums[i]-'0'<7)){dp[i]=dp[i-1]+(i-2>=0?dp[i-2]:1);continue;} dp[i]=dp[i-1]; }else {if(nums[i-1]-'0'==1||nums[i-1]-'0'==2){dp[i]=dp[i-1];continue;}return 0; }}return dp[nums.size()-1];
}
};相关文章:

数据结构与算法之[把数字翻译成字符串]动态规划
前言:最近在刷动态规划的算法题目,感觉这一类题目还是有一点难度的,但是不放弃也还是能学好的,今天给大家分享的是牛客网中的编程题目[把数字翻译成字符串],这是一道经典的面试题目,快手,字节跳…...
java 面向对象三大特性之多态 万字详解(超详细)
目录 前言 : 一、为什么需要多态 : 1.白璧微瑕 : 2.举栗(请甘雨,刻晴,钟离吃饭): 3.代码 : 4.问题 : 二、什么是多态 : 1.定义 : 2.多态的实现步骤(重要) : 三、多态的使用 : 1.多态中成员方法的使用(重要…...

git push origin master 情况
📢📢📢📣📣📣哈喽!大家好,我是「奇点」,江湖人称 singularity。刚工作几年,想和大家一同进步🤝🤝一位上进心十足的【Java ToB端大厂领…...

ElasticSearch查询优化routing
如果一个索引分片多达一百,再加上每个分片数据量大的情况下ES查询速度会慢,这种情况可以根据业务情况考虑使用_routing优化。 _routing 路由 当索引一个文档的时候,文档会被存储在一个主分片上。在存储时一般都会有多个主分片。Elasticsearch 如何知道一个文档应该放置在哪…...

【HashMap 1.7和1.8】
Java中的HashMap是一种常用的数据结构,用于存储键值对。在Java 1.7和1.8中,HashMap的实现有一些不同。 Java 1.7中的HashMap实现是基于“拉链法”的哈希表。每个哈希桶(bucket)是一个链表,存储了散列值相同的键值对。当键值对数量过多时&…...

【Zabbix实战之故障处理篇】Zabbix监控中文乱码问题解决方法
【Zabbix实战之故障处理篇】Zabbix监控中文乱码问题解决方法 一、问题展现1.查看Zabbix仪表盘2.问题分析二、检查Zabbix环境1.检查Zabbix监控主机2.检查Zabbix各组件状态三、在宿主机安装中文字体库1.安装中文字体2.查看字体文件四、安装中文字库1.查看Zabbix所有组件容器2.拷贝…...
学习(mianshi)必备-ClickHouse高性能查询/写入和常见注意事项(五)
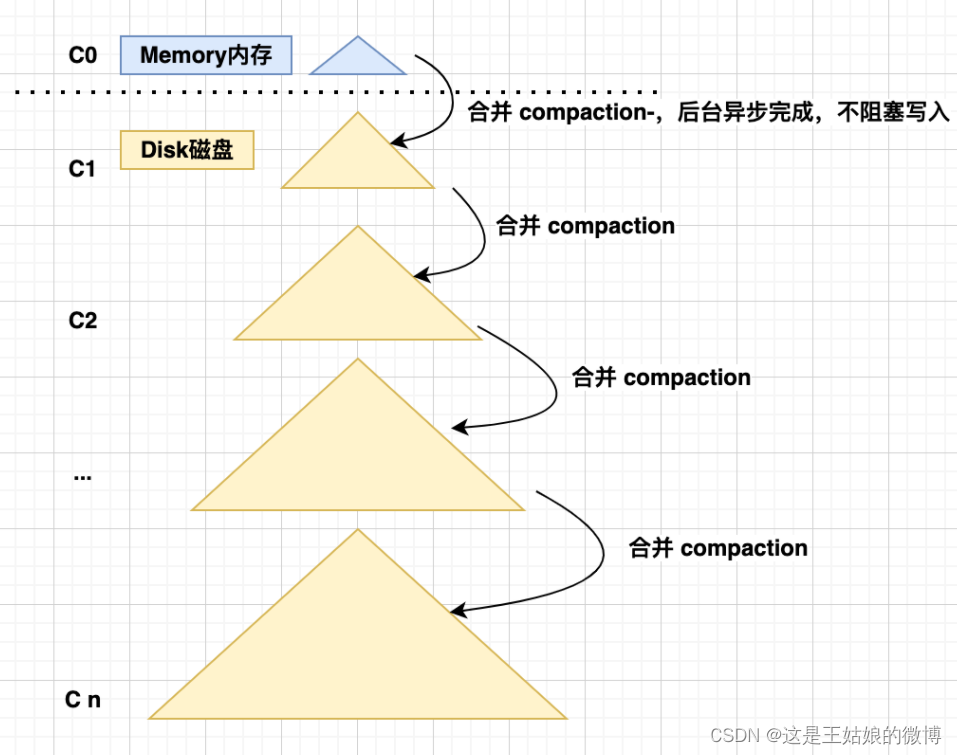
目录 一、ClickHouse高性能查询原因-稀疏索引 二、ClickHouse高性能写入-LSM-Tree存储结构 什么是LSM-Tree 三、ClickHouse的常见注意事项和异常问题排查 一、ClickHouse高性能查询原因-稀疏索引 密集索引: 在密集索引中,数据库中的每个键值都有一个索引记录&…...
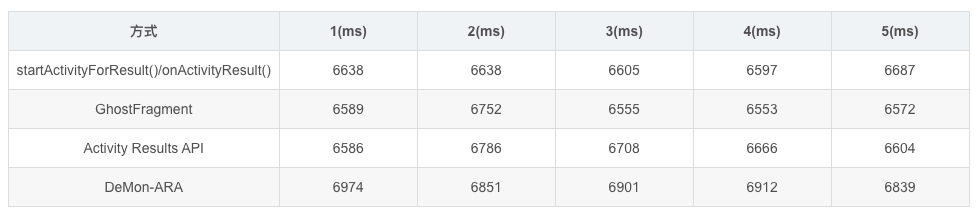
在Kotlin中探索 Activity Results API 极简的解决方案
Activity Results APIActivity Result API提供了用于注册结果、启动结果以及在系统分派结果后对其进行处理的组件。—Google官方文档https://developer.android.google.cn/training/basics/intents/result?hlzh-cn一句话解释:官方Jetpack组件用于代替startActivity…...

样式冲突太多,记一次前端CSS升级
目前平台前端使用的是原生CSSBEM命名,在多人协作的模式下,容易出现样式冲突。为了减少这一类的问题,提升研效,我调研了业界上主流的7种CSS解决方案,并将最终升级方案落地到了工程中。 样式冲突的原因 目前遇到的样式…...

如何解决报考PMP的那些问题?
关于PMP的报考条件,报考PMP都需要什么条件呢?【学历条件】:需要满足23周岁/高中毕业5年以上/大专以上学历,三个满足一个即可;【PDU条件】:报考PMP需要PDU证明(学习项目管理课程的学时证明&#…...
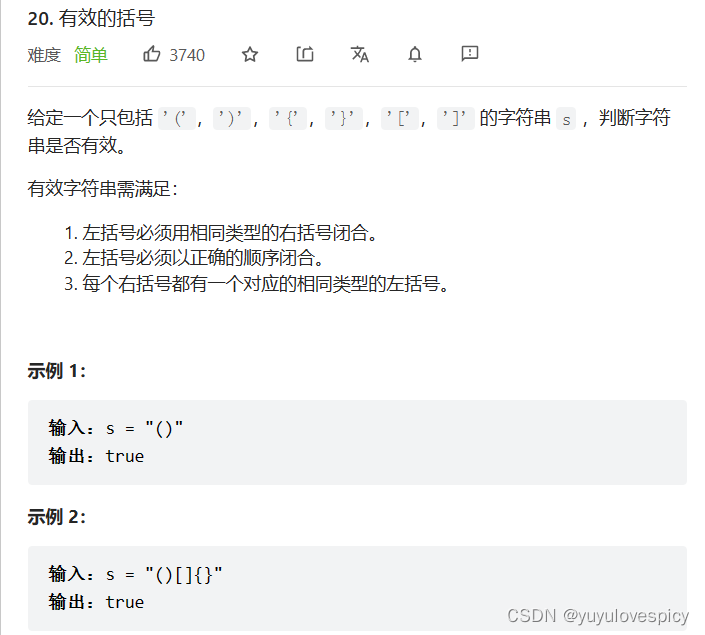
数据结构栈的经典OJ题【leetcode最小栈问题大剖析】【leetcode有效的括号问题大剖析】
目录 0.前言 1.最小栈 1.1 原题展示 1.2 思路分析 1.2.1 场景引入 1.2.2 思路 1.3 代码实现 1.3.1 最小栈的删除 1.3.2 最小栈的插入 1.3.3 获取栈顶元素 1.3.4 获取当前栈的最小值 2. 有效的括号 0.前言 本篇博客已经把两个关于栈的OJ题分块,可以根据目…...
数据结构与算法之打家劫舍(一)动态规划思想
动态规划里面一部题目打家劫舍是一类经典的算法题目之一,他有各种各样的变式,这一篇文章和大家分享一下打家劫舍最基础的一道题目,掌握这一道题目,为下一道题目打下基础。我们直接进入正题。一.题目大家如果刚接触这样的题目&…...

无人驾驶路径规划论文简要
A Review of Motion Planning Techniques for Automated Vehicles综述和分类0Motion Planning for Autonomous Driving with a Conformal Spatiotemporal Lattice从unstructured环境向structured环境的拓展,同时还从state lattice拓展到了spatiotemporal lattice从而…...
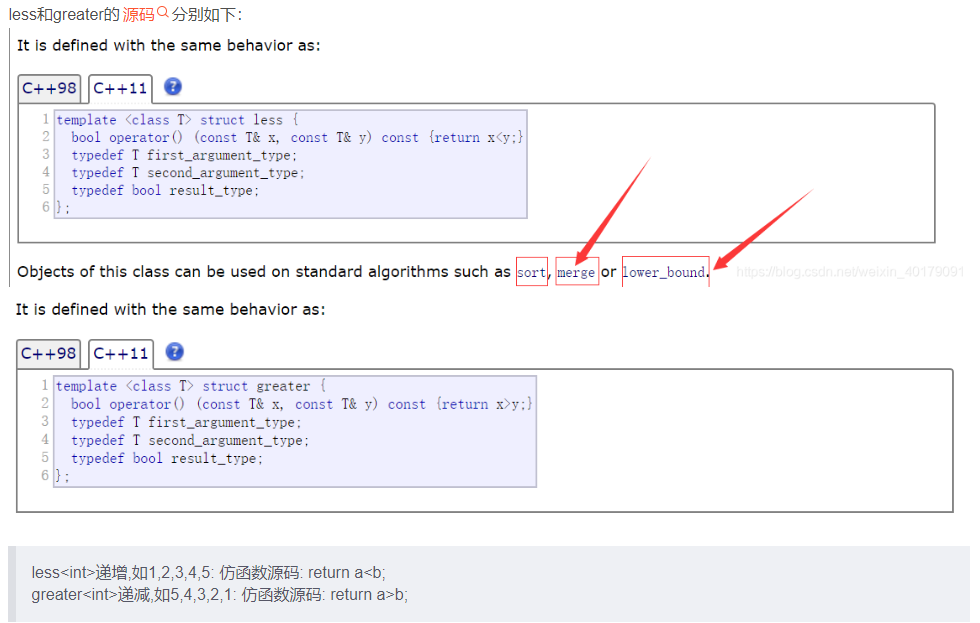
C++ sort()函数和priority_queue容器中比较函数的区别
普通的queue是一种先进先出的数据结构,元素在队列尾追加,而从队列头删除。priority_queue中元素被赋予优先级。在创建的时候根据优先级进行了按照从大到小或者从小到大进行了自动排列(大顶堆or小顶堆)。可以以O(log n) 的效率查找…...
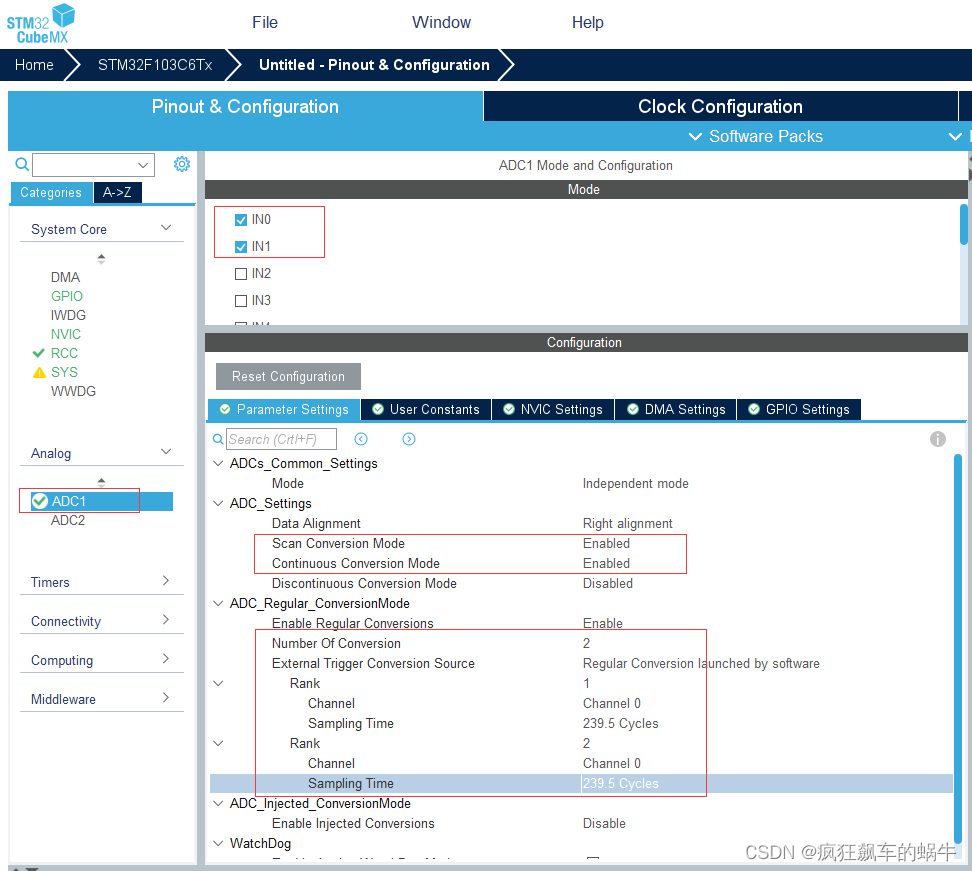
STM32开发(14)----CubeMX配置ADC
CubeMX配置ADC前言一、什么是ADC?二、实验过程1.单通道ADC采集STM32CubeMX配置代码实现2.多通道ADC采样(非DMA)STM32CubeMX配置代码实现3.多通道ADC采样(DMA)STM32CubeMX配置代码实现总结前言 本章介绍使用STM32CubeMX对ADC进行配置的方法&a…...
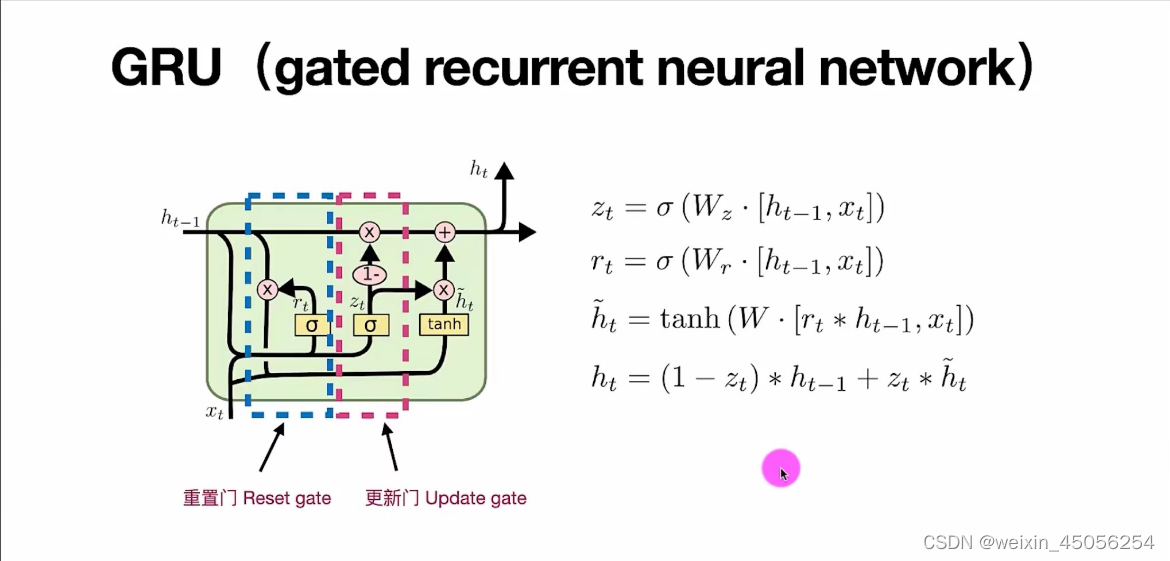
Simple RNN、LSTM、GRU序列模型原理
一。循环神经网络RNN 用于处理序列数据的神经网络就叫循环神经网络。序列数据说直白点就是随时间变化的数据,循环神经网络它能够根据这种数据推出下文结果。RNN是通过嵌含前一时刻的状态信息实行训练的。 RNN神经网络有3个变种,分别为Simple RNN、LSTM、…...
【原创】java+swing+mysql生肖星座查询系统设计与实现
今天我们来开发一个比较有趣的系统,根据生日查询生肖星座,输入生日,系统根据这个日期自动计算出生肖和星座信息反馈到界面。我们还是使用javaswingmysql去实现这样的一个系统。 功能分析: 生肖星座查询系统,顾名思义…...

CentOS 环境 OpneSIPS 3.1 版本安装及使用
文章目录1. OpenSIPS 源码下载2. 工具准备3. 编译安装4. opensips-cli 工具安装5. 启动 OpenSIPS 实例1. OpenSIPS 源码下载 使用以下命令即可下载 OpenSIPS 的源码,笔者下载的是比较稳定的 3.1 版本,读者有兴趣也可前往 官方传送门 sudo git clone htt…...

SQL95 从 Products 表中检索所有的产品名称以及对应的销售总数
描述 Products 表中检索所有的产品名称:prod_name、产品id:prod_idprod_idprod_namea0001egga0002socketsa0013coffeea0003colaOrderItems代表订单商品表,订单产品:prod_id、售出数量:quantityprod_idquantitya0001105…...

平时技术积累很少,面试时又会问很多这个难题怎么破?别慌,没事看看这份Java面试指南,解决你的小烦恼!
前言技术面试是每个程序员都需要去经历的事情,随着行业的发展,新技术的不断迭代,技术面试的难度也越来越高,但是对于大多数程序员来说,工作的主要内容只是去实现各种业务逻辑,涉及的技术难度并不高…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
