图论06-【无权无向】-图的遍历并查集Union Find-力扣695为例
文章目录
- 1. 代码仓库
- 2. 思路
- 2.1 UF变量设计
- 2.2 UF合并两个集合
- 2.3 查找当前顶点的父节点 find(element)
- 3. 完整代码
1. 代码仓库
https://github.com/Chufeng-Jiang/Graph-Theory
2. 思路
2.1 UF变量设计

parent数组保存着每个节点所指向的父节点的索引,初始值为当前顶点编号,指向自己。
后期在合并的时候均指向其合并的另一个元素的父节点,也就是p->a, q->q,合并p和q时,改变q的指向,q->a.
最终a下面挂两个节点,分别为p, q.
//parent数组中保存着每个节点所指向的父节点的索引
private int[] parent;sz数组来保存每个根节点所代表的子树中元素的数量
private int[] sz;
2.2 UF合并两个集合
查找两个元素的父节点,父节点相同则属于同一个集合
public void unionElements(int p, int q) {int pRoot = find(p); // 找到p的父节点int qRoot = find(q); // 找到q的父节点if (pRoot == qRoot) // 如果pq的父节点相同,说明在同一个集合内return;parent[pRoot] = qRoot; //如果不相同,将p的父节点挂到q的父节点下,进行合并sz[qRoot] += sz[pRoot]; //q的集合大小合并
}
2.3 查找当前顶点的父节点 find(element)
递归查找父节点,只要不满足p = parent[p],就肯定没有到达最上层。find(parent[p])为查找p节点的
public int find(int p) {if (p != parent[p]) //还没找到根节点parent[p] = find(parent[p]); //递归实现//p = parent[p]时,就是父节点return parent[p];
}
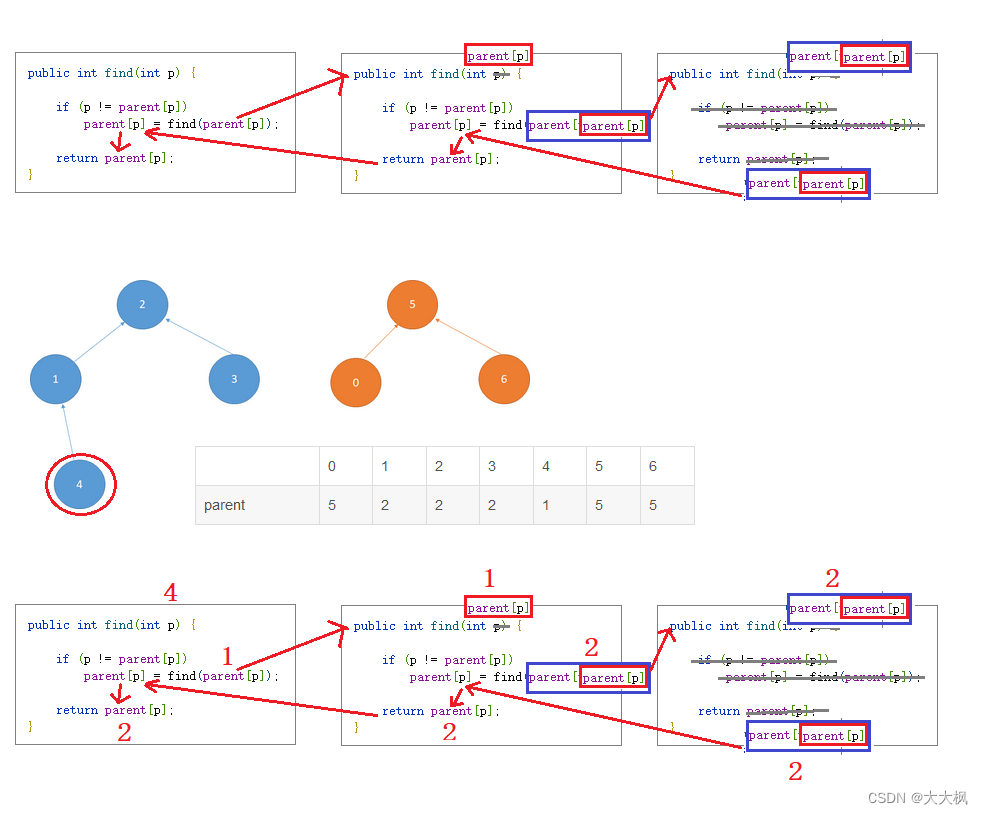
3. 完整代码
public class Union_Find {class UF {private int[] parent; //parent数组中保存着每个节点所指向的父节点的索引private int[] sz;public UF(int n) {parent = new int[n];sz = new int[n];for (int i = 0; i < n; i++) {parent[i] = i; //初始化的时候当前节点的父节点都是自己sz[i] = 1; //当前所属集合的大小}}// 不断去查询自己的父亲节点, 直到到达根节点// 根节点的特点: parent[p] == ppublic int find(int p) {if (p != parent[p]) //还没找到根节点parent[p] = find(parent[p]); //递归实现return parent[p]; //终于找到根节点}public boolean isConnected(int p, int q) {return find(p) == find(q);}public void unionElements(int p, int q) {int pRoot = find(p); //找到p的父节点int qRoot = find(q); //找到q的父节点if (pRoot == qRoot)//如果pq的父节点相同,说明在同一个集合内return;parent[pRoot] = qRoot; //如果不相同,将p的父节点挂到q的父节点下,进行合并sz[qRoot] += sz[pRoot]; //q的集合大小合并}public int size(int p) {return sz[find(p)];}}private int[][] dirs = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};private int R, C;public int maxAreaOfIsland(int[][] grid) {if (grid == null) return 0;R = grid.length;if (R == 0) return 0;C = grid[0].length;if (C == 0) return 0;UF uf = new UF(R * C);for (int v = 0; v < R * C; v++) {int x = v / C, y = v % C;if (grid[x][y] == 1)for (int d = 0; d < 4; d++) {int nextx = x + dirs[d][0], nexty = y + dirs[d][1];if (inArea(nextx, nexty) && grid[nextx][nexty] == 1) {int next = nextx * C + nexty;uf.unionElements(v, next);}}}int res = 0;for (int v = 0; v < R * C; v++) {int x = v / C, y = v % C;if (grid[x][y] == 1)res = Math.max(res, uf.size(v)); //遍历找到最大的size}return res;}private boolean inArea(int x, int y) {return x >= 0 && x < R && y >= 0 && y < C;}
}
相关文章:

图论06-【无权无向】-图的遍历并查集Union Find-力扣695为例
文章目录 1. 代码仓库2. 思路2.1 UF变量设计2.2 UF合并两个集合2.3 查找当前顶点的父节点 find(element) 3. 完整代码 1. 代码仓库 https://github.com/Chufeng-Jiang/Graph-Theory 2. 思路 2.1 UF变量设计 parent数组保存着每个节点所指向的父节点的索引,初始值为…...
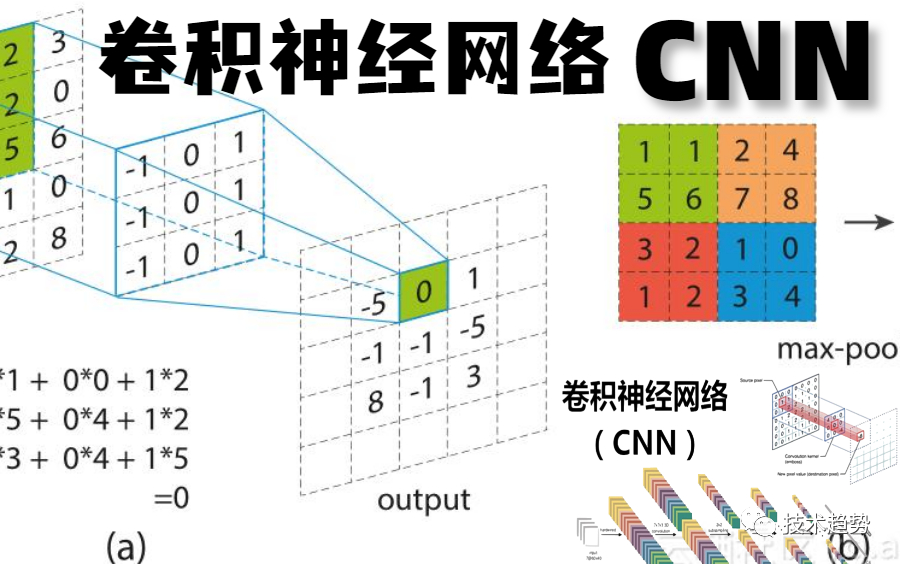
什么是卷积神经网络?解决了什么问题?
什么是卷积神经网络? 卷积神经网络(Convolutional Neural Network,CNN)是一种深度神经网络模型,主要用于图像识别、语音识别和自然语言处理等任务。它通过卷积层、池化层和全连接层来实现特征提取和分类。 解决了什么问…...

Golang数组:全面指南与实际示例
揭示Golang数组的威力:从基础到高级技巧 Golang数组是数据存储的基本构建块,为开发人员提供了多种可能性。在这篇正式的博客文章中,我们将探讨Golang数组,从基础知识到高级技巧。通过实际示例和正式的语气,我们将揭示…...

程序连接oracle查询数据的环境配置
连接oracle 数据库真麻烦,还是MySQL方便 Oracle Instant Client 这个东西的版本跟oracle的版本是有讲究的,引用文档的说明 Oracle 标准的客户端-服务器网络互操作性允许不同版本的 Oracle 客户端和 Oracle 数据库之间的连接。有关经过认证的配置&#…...

【BIGRU预测】基于双向门控循环单元的多变量时间序列预测(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
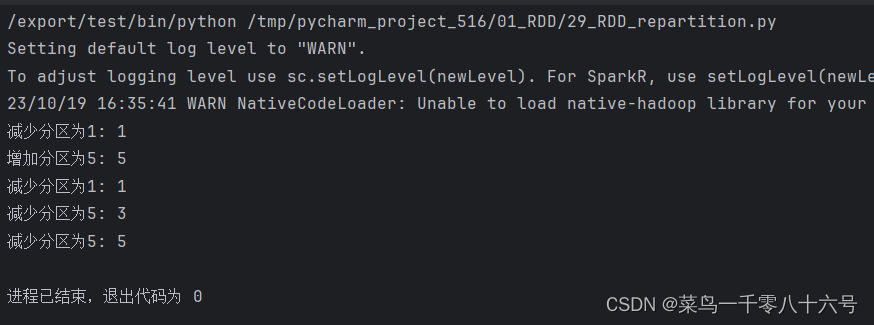
RDD算子操作(基本算子和常见算子)
目录 一、基本算子 1.map算子 2.flatMap算子 3.filter算子 4.foreach算子 5.saveAsTextFile算子 6.redueceByKey算子 二、常用Transformation算子 1.mapValues算子 2.groupBy算子 3.distinct算子 4.union算子 5.join算子 6.intersection算子 7.glom算子 8.groupByKey算…...

互联网Java工程师面试题·Java 面试篇·第五弹
目录 79、适配器模式和装饰器模式有什么区别? 80、适配器模式和代理模式之前有什么不同? 81、什么是模板方法模式? 82、什么时候使用访问者模式? 83、什么时候使用组合模式? 84、继承和组合之间有什么不同&#…...

常见的测试理论面试问题
请解释软件生存周期是什么? 软件生存周期是指从软件开发到维护的过程,包括可行性研究、需求分析、软件设计、编码、测试、发布和维护等活动。这个过程也被称为“生命周期模型”。 软件测试的目的是什么? 软件测试的目的是发现软件中的错误…...

把JS中的map方法玩出花来
一 map是什么 map(callbackFn) map(callbackFn, thisArg)map() 方法是一个迭代方法。它为数组中的每个元素调用一次提供的 callbackFn 函数,并用结果构建一个新数组。 参数 callbackFn 数组中的每个元素执行的函数。它的返回值作为一个元素被添加为新数组中。该…...
)
液晶显示计算器(延时程序)
#include "delay.h" /*------------------------------------------------ uS延时函数,含有输入参数 unsigned char t,无返回值 unsigned char 是定义无符号字符变量,其值的范围是 0~255 这里使用晶振12M,精确延时请…...

线性代数2:梯队矩阵形式
图片来自 Europeana on Unsplash 一、前言 欢迎阅读的系列文章的第二篇文章,内容是线性代数的基础知识,线性代数是机器学习背后的基础数学。在我之前的文章中,我介绍了线性方程和系统、矩阵符号和行缩减运算。本文将介绍梯队矩阵形式…...
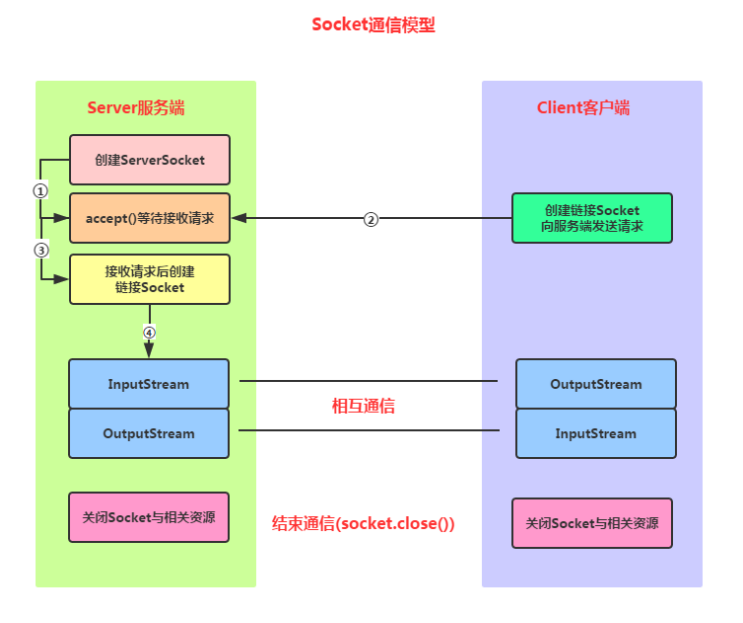
【JavaEE】网络编程(网络编程基础、Socket套接字)
一、网络编程基础 1.1、什么是网络编程? 网络编程,指网络上的主机,通过不同的进程,以编程的方式实现网络通信(或称为网络数据传输) 注意:我们只要满足进程不同就行;所以即便是同一…...

Node学习笔记之模块化
一、介绍 1.1 什么是模块化与模块 ? 将一个复杂的程序文件依据一定规则(规范)拆分成多个文件的过程称之为 模块化 其中拆分出的 每个文件就是一个模块 ,模块的内部数据是私有的,不过模块可以暴露内部数据以便其他 模块使用 1…...

用matlab求解线性规划
文章目录 1、用单纯形表求解线性规划绘制单纯形表求解: 2、用matlab求解线性规划——linprog()函数问题:补充代码:显示出完整的影子价格向量 1、用单纯形表求解线性规划 求解线性规划 m i n − 3 x 1 − 4 x 2 x 3 min -3x_1-4x_2x_3 min−…...
)
antd获取/更改form表单数据(表单域数据)
创建ref引用 formRef React.createRef();表单和ref绑定 //ref{this.formRef} 先给Form <Form ref{this.formRef} name"control-ref" onFinish{this.onFinish}><Form.Item name"name" label"Name" rules{[{ required: true }]}>…...

Go学习第三章——运算符与进制
Go学习第三章——运算符与进制 1 算术运算符2 关系运算符3 逻辑运算符4 赋值运算符5 其他运算符5.1 位运算符5.2 跟指针有关的运算符 6 运算符的优先级7 获取用户终端输入8 进制转换8.1 进制基本使用8.2 进制之间的转换8.3 原码 反码 补码8.4 位运算符详解 运算符是—种特殊的符…...
H3C IMC dynamiccontent.properties.xhtm 远程命令执行
我举手向苍穹,并非一定要摘星取月,我只是需要这个向上的、永不臣服的姿态。 构造payload: /imc/javax.faces.resource/dynamiccontent.properties.xhtml pfdrtsc&lnprimefaces&pfdriduMKljPgnOTVxmOB%2BH6%2FQEPW9ghJMGL3PRdkfmbii…...
【技能树笔记】网络篇——练习题解析(八)
目录 前言 一、LAN技术 1.1 堆叠与集群 1.2 MSTP的特点 二、WAN技术 2.1 PPP链路建立 2.2 PPPoE 2.3 组播 2.3.1 组播的IP 2.3.2 组播分发树 2.3.3 组播协议 三、IPv6基础 3.1 IPv6地址 3.2 IPv6协议 3.3 IPv6过渡技术 总结 🌈嗨!我是Filotimo__…...
)
laravel框架介绍(二)
方法1.windows 可以直接下载 Composer-Setup.exe 方法2.配置php.exe目录环境变量,下载 composer.phar和php.exe平级目录, 新建 composer.bat 文件编辑以下内容 php "%~dp0composer.phar" %* 运行composer.bat ,出现版本号为成功 执行 composer self-update 以保持 Co…...

USB学习(1):USB基础之接口类型、协议标准、引脚分布、架构、时序和数据格式
连接计算机外围设备最简单的方法是通过USB(通用串行总线)。USB是即插即用接口,可以将扫描仪、打印机、数码相机、闪存驱动器等计算机外围设备连接到计算机上。本篇文章就来介绍一下USB的一些基础知识,包括。 文章目录 1 接口类型和标准规范2 引脚分布3 …...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
