macrodata数据集在Python统计建模和计量经济学中的应用
目录
- 一、数据介绍
- 二、应用
- 三、statsmodels 统计模块
- 四、使用 statsmodels 统计模块分析 macrodata.csv 数据集
- 参考
一、数据介绍
macrodata.csv是一个示例数据集,通常用于统计分析和计量经济学中的教育和训练目的。这个数据集通常包括以下列:
year(年份):表示数据观察的年份。
quarter(季度):表示数据观察的季度(通常是1至4)。
realgdp(实际国内生产总值):表示实际国内生产总值的数值,通常以美元为单位。
realcons(实际消费支出):表示实际消费支出的数值,通常以美元为单位。
realinv(实际投资支出):表示实际投资支出的数值,通常以美元为单位。
realgovt(实际政府支出):表示实际政府支出的数值,通常以美元为单位。
realdpi(实际可支配个人收入):表示实际可支配个人收入的数值,通常以美元为单位。
cpi(消费者物价指数):表示消费者物价指数的数值。
m1(货币供应量M1):表示M1货币供应量的数值。
tbilrate(国债利率):表示国债利率的数值。
unemp(失业率):表示失业率的百分比。
pop(人口):表示总人口数。
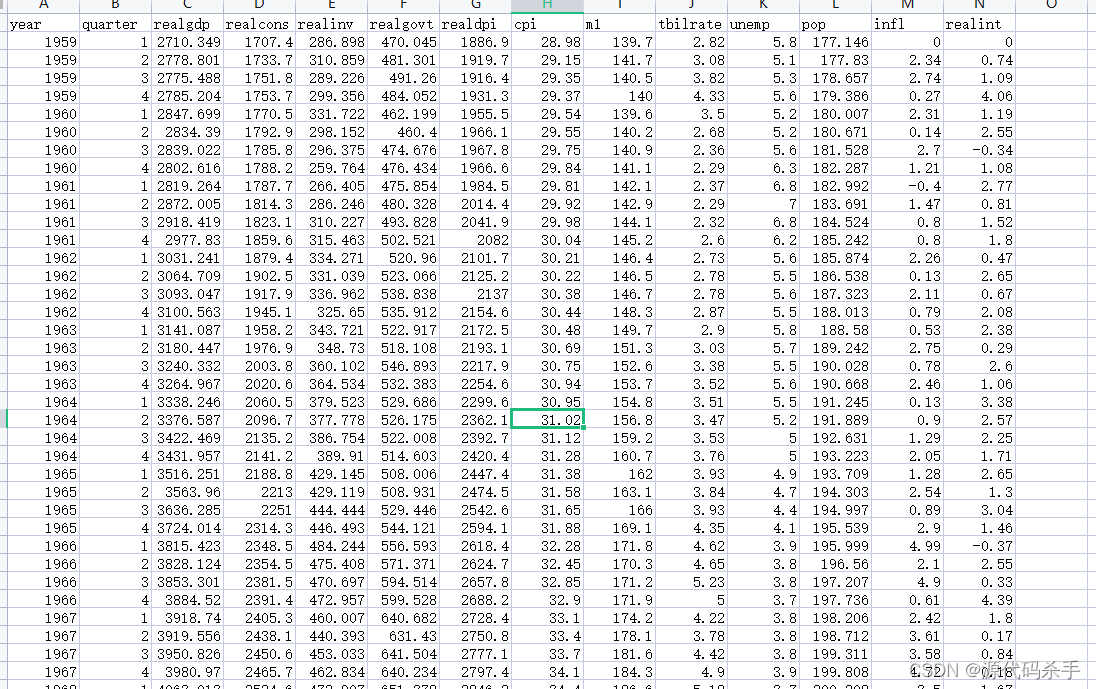
这些列通常用于经济数据分析和时间序列分析,以探讨宏观经济现象和趋势。您可以使用统计分析软件(例如Python中的Pandas和Statsmodels库)来导入和分析这些数据,以获取有关经济变量之间关系的见解。
二、应用
macrodata.csv 数据集在Python中的统计建模和计量经济学中应用广泛,特别是在使用Statsmodels等统计分析库进行经济数据分析时。以下是一些使用该数据集的典型应用场景:
时间序列分析:macrodata 数据集通常包含了多年的经济指标数据,可以用于时间序列分析。研究者可以使用这些数据来探索不同经济变量的趋势、季节性和周期性变化。
计量经济学模型:研究者可以使用这个数据集来估计和测试各种计量经济学模型,如线性回归、多元回归、时间序列模型和面板数据模型。这些模型可以用于研究不同经济变量之间的关系,例如 GDP 与消费支出之间的关系。
政策分析:政府和政策制定者可以使用 macrodata 数据集来评估不同政策措施对经济的影响。例如,他们可以分析政府支出与失业率之间的关系,以确定政府支出对就业的潜在影响。
预测和预测建模:研究者可以使用这个数据集来构建经济预测模型。这些模型可以用来预测未来的经济变量,帮助企业、投资者和政府做出决策。
教育和培训:macrodata 数据集也用于教育和培训,帮助学生和专业人士学习如何使用Python进行计量经济学分析。这个数据集通常用作教育材料的一部分。
在Python中,您可以使用众多的库和工具进行 macrodata 数据集的分析,包括:
Pandas:用于数据导入、清洗和转换。
NumPy:用于数值计算和数据操作。
Matplotlib 和 Seaborn:用于数据可视化和绘图。
Statsmodels:用于估计统计模型,如线性回归、时间序列模型和面板数据模型。
Scikit-learn:用于机器学习模型的建模和预测。
Jupyter Notebook:用于交互式分析和报告编写。
三、statsmodels 统计模块
statsmodels 是一个 Python 包,它为 scipy 提供了统计计算的补充,包括描述性统计以及统计模型的估计和推理。
最新版本的文档位于
https://www.statsmodels.org/stable/
开发版本的文档位于
https://www.statsmodels.org/dev/
发行说明中强调了最近的改进
https://www.statsmodels.org/stable/release/
文档备份可在https://statsmodels.github.io/stable/ 和https://statsmodels.github.io/dev/获取。
主要特点
- 线性回归模型:
普通最小二乘
广义最小二乘法
加权最小二乘法
具有自回归误差的最小二乘法
分位数回归
递归最小二乘法 - 具有混合效应和方差分量的混合线性模型
- GLM:广义线性模型,支持所有单参数指数族分布
- 二项式和泊松的贝叶斯混合 GLM
- GEE:单向聚类或纵向数据的广义估计方程
- 离散模型:
Logit 和 Probit
多项式 Logit (MNLogit)
泊松和广义泊松回归
负二项式回归
零膨胀计数模型
RLM:稳健的线性模型,支持多个 M 估计器。 - 时间序列分析:时间序列分析模型
完整的 StateSpace 建模框架
季节性 ARIMA 和 ARIMAX 模型
VARMA 和 VARMAX 模型
动态因子模型
未观察到的组件模型
马尔可夫切换模型 (MSAR),也称为隐马尔可夫模型 (HMM)
单变量时间序列分析:AR、ARIMA
向量自回归模型、VAR 和结构 VAR
矢量纠错模型,VECM
指数平滑、Holt-Winters
时间序列的假设检验:单位根、协整等
用于时间序列分析的描述性统计和过程模型 - 生存分析:
比例风险回归(Cox 模型)
幸存者函数估计 (Kaplan-Meier)
累积关联函数估计 - 多变量:
缺失数据的主成分分析
旋转因子分析
多元方差分析
典型相关性
四、使用 statsmodels 统计模块分析 macrodata.csv 数据集
要使用 statsmodels 统计模块分析 macrodata.csv 数据集,您需要执行以下一般步骤:
导入必要的库:首先,导入 Python 库,包括 pandas 用于数据操作和 statsmodels 用于统计分析。确保您已经安装了这些库,可以使用 pip 安装它们。
import pandas as pd
import statsmodels.api as sm
加载数据:使用 Pandas 加载 macrodata.csv 数据集,并查看数据的前几行,以确保数据正确加载。
data = pd.read_csv('macrodata.csv')
print(data.head())
数据准备:根据您的分析目标,选择感兴趣的自变量(解释变量)和因变量(响应变量)。将数据划分为 X(自变量)和 y(因变量)。
X = data[['realgdp', 'realcons', 'realinv', 'realgovt']]
y = data['realdpi']
添加截距项:通常,您会为模型添加一个截距项,除非您明确不希望添加。
X = sm.add_constant(X) # 添加常数(截距项)
拟合模型:使用 statsmodels 来拟合您感兴趣的模型。以下是一个线性回归模型的示例:
model = sm.OLS(y, X).fit() # 拟合线性回归模型
查看模型摘要:使用模型摘要方法来查看回归结果的详细信息,包括系数、标准误差、P-值等。
print(model.summary())
进行统计测试:您可以使用模型进行统计测试,如假设检验,来评估模型的有效性。例如,检验系数是否显著不同于零。
print(model.t_test([0, 1, 0, 0, 0])) # 检验第一个系数是否等于零
做出预测:使用拟合的模型进行预测。您可以预测因变量的值或进行其他类型的分析。
predictions = model.predict(X)
以上是一个基本的分析框架,您可以根据具体的问题和分析目标进行进一步的自定义。statsmodels 还支持其他类型的模型,包括时间序列模型、逻辑回归模型等,具体操作方式可能会有所不同。根据您的需要,您可以选择适当的模型和方法进行分析。
参考
详细参考:https://github.com/statsmodels/statsmodels/tree/main
数据下载:https://github.com/statsmodels/statsmodels/tree/main
相关文章:

macrodata数据集在Python统计建模和计量经济学中的应用
目录 一、数据介绍二、应用三、statsmodels 统计模块四、使用 statsmodels 统计模块分析 macrodata.csv 数据集参考 一、数据介绍 macrodata.csv是一个示例数据集,通常用于统计分析和计量经济学中的教育和训练目的。这个数据集通常包括以下列: year&am…...

【C++进阶(九)】C++多态深度剖析
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:C从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 多态 1. 前言2. 多态的概念以及定义3. 多态的实…...

第二节——Vue 基本介绍
一、MV*的理解 1、概念 在计算机编程领域,MV*(也称为MVC、MVP、MVVM等)是一种用于组织和设计应用程序结构的模式。这些模式旨在实现应用程序的解耦、可维护性和可扩展性。MV代表着Model-View-(表示控制器或视图模型等其他组件&a…...
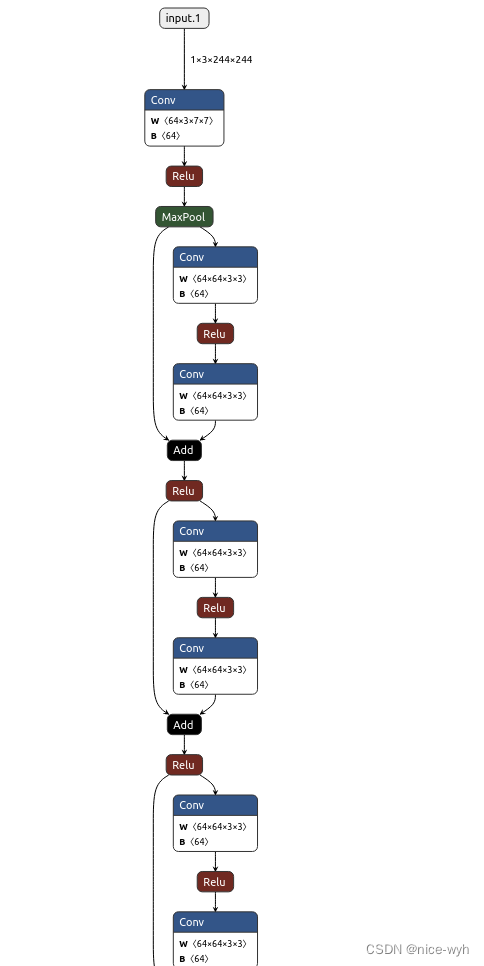
基于ResNet34的花朵分类
一.数据集准备 新建一个项目文件夹ResNet,并在里面建立data_set文件夹用来保存数据集,在data_set文件夹下创建新文件夹"flower_data",点击链接下载花分类数据集https://storage.googleapis.com/download.tensorflow.org/example_i…...

[计算机提升] 数据及相关概念
1.9 数据及相关概念 1.9.1 数据、信息 在Windows系统中,数据是指事实或信息的集合,可以是数字、文本、图像、声音等形式的内容。数据是计算机系统中处理和操作的基本元素,是信息的表现形式和载体。 与信息相比,数据的范围更广泛…...
)
第18章 SpringCloud生态(二)
18.11 说说你了解的负载均衡算法 难度:★★ 重点:★★★★ 白话解析 常用的负载均衡算法有: 1、轮询(Round Robin):说白了就是让服务器排好队,一个个轮着来调用;Ribbon默认采用该算法。 优点:实现起来简单; 缺点:服务器性能不一样的情况下,导致能力强的会经常空闲…...

【Android】BRVAH多布局实现
前言 基于3.0.4版本的BRVAH框架实现的 实现方法 1.创建多个不同类型的布局(步骤忽略) 2.创建数据实体类 数据类要实现【MultiItemEntity】接口 class MyMultiItemEntity(//获取布局类型override var itemType: Int,var tractorRes: Int? null,va…...

AWS SAP-C02教程9-节省成本
SAP-C01变成SAP-C02的时候,最大的变化就是没有把成本单独列出一个模块,但是成本依然包含在各个其它模块之中,所以成本还是很重要的。本章将列举一些成本优化方案以及一些成本辅助功能。 目录 1 Cost Allocation Tags2 Trusted Advisor2.1 AWS Support Plans2.2 基本特性2.3…...
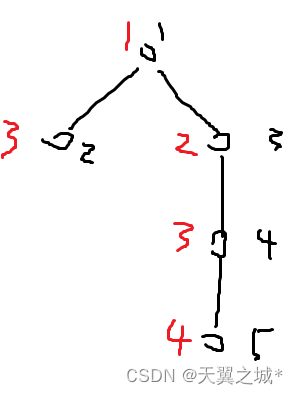
[CSP-S 2023] 种树 —— 二分+前缀和
This way 题意: 一开始以为是水题,敲了一个二分贪心检查的代码,20分。发现从根往某个节点x走的时候,一路走来的子树上的节点到已栽树的节点的距离会变短,那么并不能按照初始情况贪心。 于是就想着检查时候用线段树…...

【LeetCode周赛】LeetCode第368场周赛
目录 元素和最小的山形三元组 I元素和最小的山形三元组 II合法分组的最少组数 元素和最小的山形三元组 I 给你一个下标从 0 开始的整数数组 nums 。 如果下标三元组 (i, j, k) 满足下述全部条件,则认为它是一个山形三元组 : i < j < k nums[i] &l…...
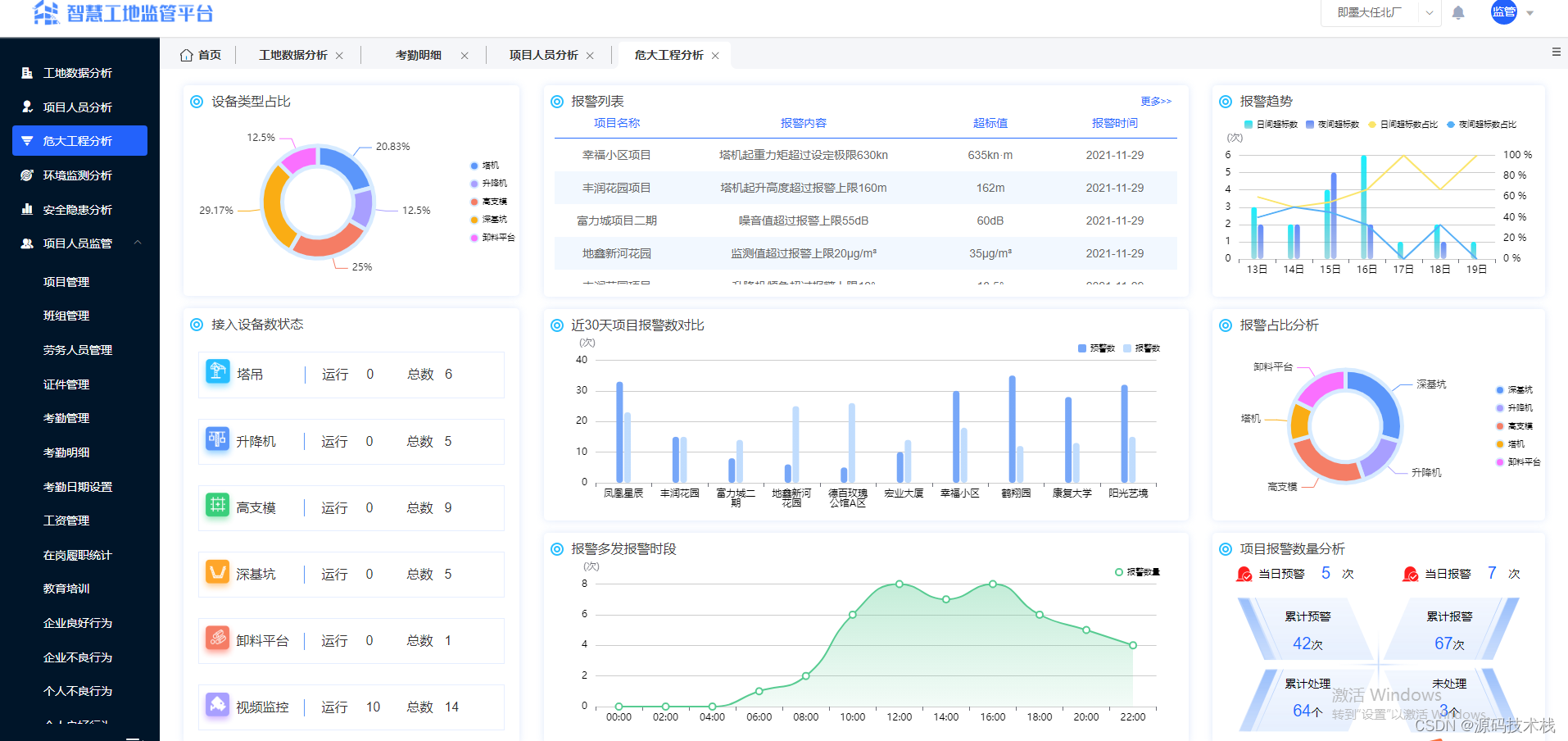
【智慧工地源码】基于AI视觉技术赋能智慧工地
伴随着技术的不断发展,信息化手段、移动技术、智能穿戴及工具在工程施工阶段的应用不断提升,智慧工地概念应运而生,庞大的建设规模催生着智慧工地的探索和研发。 建筑施工具有周期长、环境复杂、工序繁杂、人员流动性大等特点,所以…...

云服务器搭建Hadoop分布式
文章目录 1.服务器配置2.Java环境3. 安装Hadoop4. 集群配置5. 编写集群的启动脚本 1.服务器配置 服务器主机名配置115.157.197.82s110核115.157.197.84s210核115.157.197.109s310核115.157.197.31s410核115.157.197.60gracal10核 所有的软件安装在/opt/module下,软…...

2678. 老人的数目
给你一个下标从 0 开始的字符串 details 。details 中每个元素都是一位乘客的信息,信息用长度为 15 的字符串表示,表示方式如下: 前十个字符是乘客的手机号码。 接下来的一个字符是乘客的性别。 接下来两个字符是乘客的年龄。 最后两个字符是…...
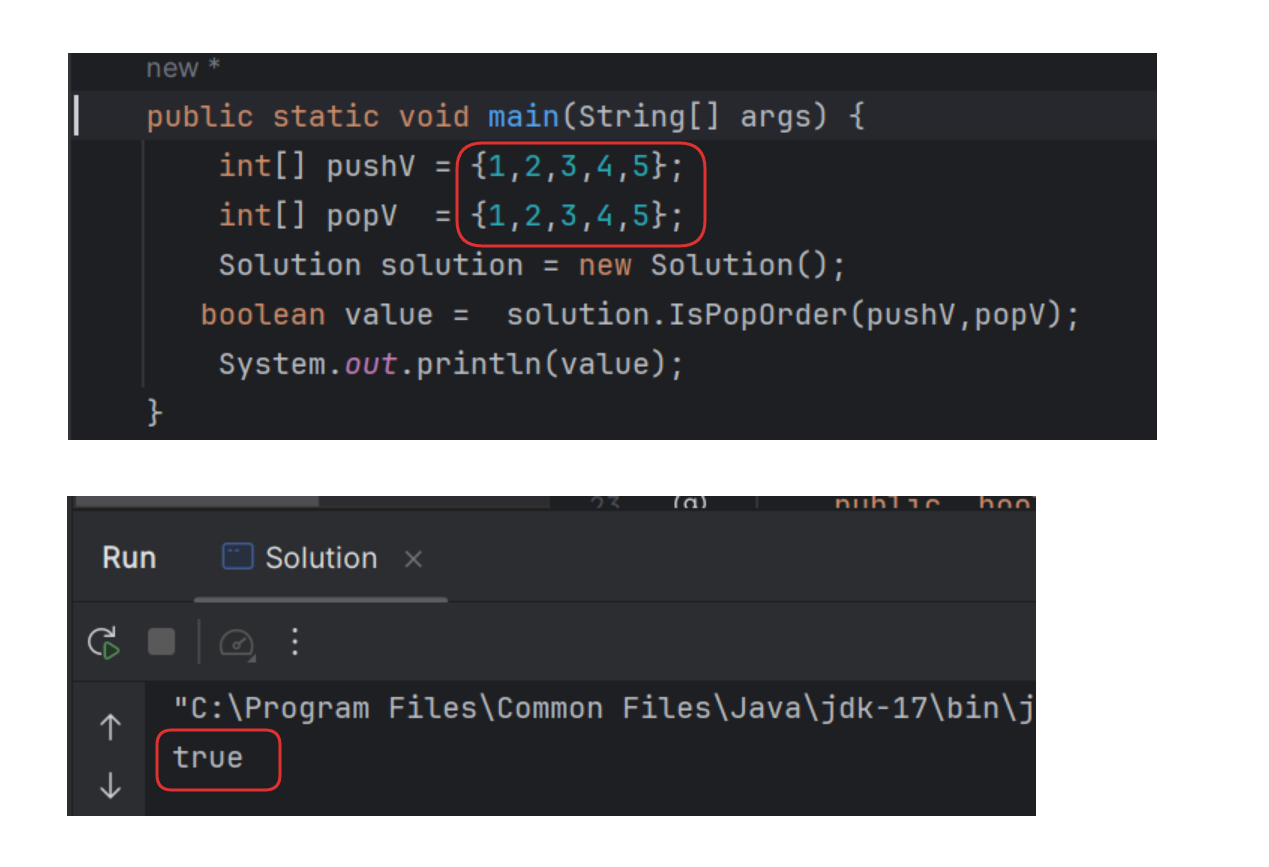
【刷题-牛客】出栈、入栈的顺序匹配 (代码+动态演示)
【刷题-牛客】出栈、入栈的顺序匹配 (代码动态演示) 文章目录 【刷题-牛客】出栈、入栈的顺序匹配 (代码动态演示) 解题思路 动图演示完整代码多组测试 💗题目描述 💗: 输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个…...
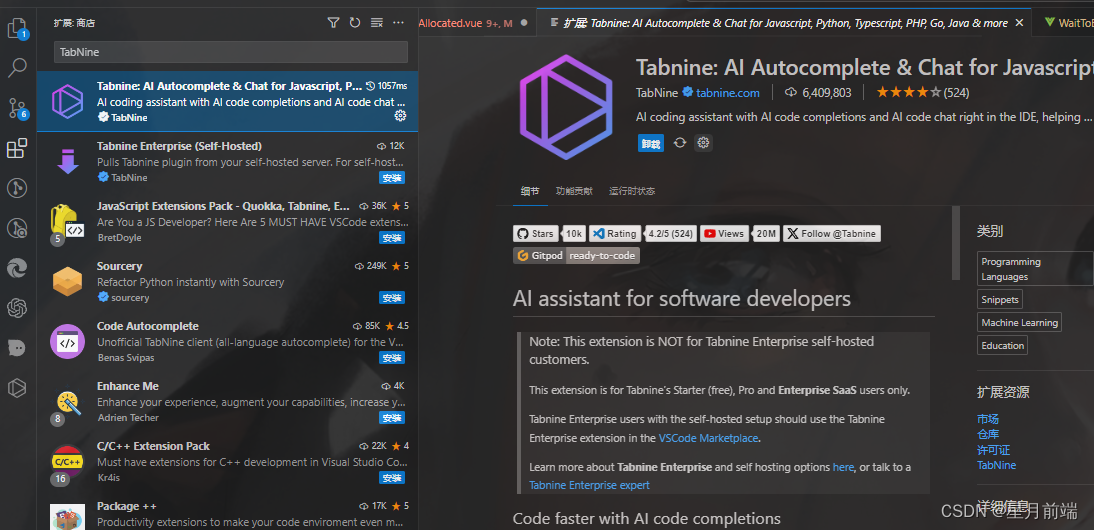
vscode类似GitHub Copilot的插件推荐
由于GitHub Copilot前段时间学生认证的账号掉了很多,某宝激活也是价格翻了几倍,而却,拿来用一天就掉线,可以试试同类免费的插件哦。 例如:TabNine,下载插件后,他会提示你登录,直接登…...

Html -- 文字时钟
Html – 文字时钟 文字时钟,之前在Android上实现了相关效果,闲来无事,弄个网页版的玩玩。。。直接上代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><titl…...

快问快答:关于线上流量卡“归属地随机”几个问题!
在网上办过流量卡的朋友应该都知道,资费虽然便宜,但是归属地却是异地,今天小编就给大家聊一聊关于流量卡归属地的问题。 网上的流量卡都是归属地随机的卡,今天小编以问答的方式给大家普及一下,如果对于归属地有疑问…...

Linux常用命令——clock命令
在线Linux命令查询工具 clock 用于调整 RTC 时间。 补充说明 clock命令用于调整 RTC 时间。 RTC 是电脑内建的硬件时间,执行这项指令可以显示现在时刻,调整硬件时钟的时间,将系统时间设成与硬件时钟之时间一致,或是把系统时间…...
澎湃OS上线:小米告别MIUI,跟小米汽车Say Hi
作者 | Amy 编辑 | 德新 10月17日,雷军发博官宣,「小米将启用全新操作系统,小米澎湃OS(Xiaomi HyperOS)」。 短短几百字的微博,数次提到了「小米汽车」: 小米向人车家全生态迈进,…...

域名不部署SSL证书有什么影响?
SSL证书是保护网站数据传输安全的重要工具,通过加密用户和服务器之间的通信来确保数据的保密性和完整性。然而,如果一个域名没有部署SSL证书,会对网站和用户产生一系列的负面影响。下文中将介绍域名不部署SSL证书的影响,并提供相应…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

表单设计器拖拽对象时添加属性
背景:因为项目需要。自写设计器。遇到的坑在此记录 使用的拖拽组件时vuedraggable。下面放上局部示例截图。 坑1。draggable标签在拖拽时可以获取到被拖拽的对象属性定义 要使用 :clone, 而不是clone。我想应该是因为draggable标签比较特。另外在使用**:clone时要将…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...
