Leetcode1971. 寻找图中是否存在路径
Every day a Leetcode
题目来源:1971. 寻找图中是否存在路径
解法1:并查集
并查集介绍:并查集详解
代码:
/** @lc app=leetcode.cn id=1971 lang=cpp** [1971] 寻找图中是否存在路径*/// @lc code=start
class UnionFind
{vector<int> father, size;public:UnionFind(int n) : father(n), size(n, 1){// iota函数可以把数组初始化为 0 到 n-1iota(father.begin(), father.end(), 0);}int find(int x){if (x == father[x])return x;elsereturn find(father[x]);}void connect(int p, int q){int fa_p = find(p), fa_q = find(q);if (fa_p != fa_q)father[fa_p] = fa_q;}bool isConnected(int p, int q){return find(p) == find(q);}
};class Solution
{
public:bool validPath(int n, vector<vector<int>> &edges, int source, int destination){UnionFind uf(n);for (vector<int> &edge : edges)uf.connect(edge[0], edge[1]);return uf.isConnected(source, destination);}
};
// @lc code=end
结果:
复杂度分析:
时间复杂度:O(n+m×α(m)),其中 n 是图中的顶点数,m 是图中边的数目,α 是反阿克曼函数。并查集的初始化需要 O(n) 的时间,然后遍历 m 条边并执行 m 次合并操作,最后对 source 和 destination 执行一次查询操作,查询与合并的单次操作时间复杂度是 O(α(m)),因此合并与查询的时间复杂度是 O(m×α(m)),总时间复杂度是 O(n+m×α(m))。
空间复杂度:O(n),其中 n 是图中的顶点数。并查集需要 O(n) 的空间。
解法2:深度优先搜索
首先从顶点 source 开始遍历并进行递归搜索。搜索时每次访问一个顶点 vertex 时,如果 vertex 等于 destination 则直接返回,否则将该顶点设为已访问,并递归访问与 vertex 相邻且未访问的顶点 next。如果通过 next 的路径可以访问到 destination,此时直接返回 true,当访问完所有的邻接节点仍然没有访问到 destination,此时返回 false。
代码:
class Solution
{
public:bool dfs(int source, int destination, vector<vector<int>> &adj, vector<bool> &visited){if (source == destination){return true;}visited[source] = true;for (int next : adj[source]){if (!visited[next] && dfs(next, destination, adj, visited)){return true;}}return false;}bool validPath(int n, vector<vector<int>> &edges, int source, int destination){vector<vector<int>> adj(n);for (auto &edge : edges){int x = edge[0], y = edge[1];adj[x].emplace_back(y);adj[y].emplace_back(x);}vector<bool> visited(n, false);return dfs(source, destination, adj, visited);}
};
结果:
复杂度分析:
时间复杂度:O(n+m),其中 n 表示图中顶点的数目,m 表示图中边的数目。
空间复杂度:O(n+m),其中 n 表示图中顶点的数目,m 表示图中边的数目。空间复杂度主要取决于邻接顶点列表、记录每个顶点访问状态的数组和递归调用栈,邻接顶点列表需要 O(m+n) 的存储空间,记录每个顶点访问状态的数组和递归调用栈分别需要 O(n) 的空间。
相关文章:

Leetcode1971. 寻找图中是否存在路径
Every day a Leetcode 题目来源:1971. 寻找图中是否存在路径 解法1:并查集 并查集介绍:并查集详解 代码: /** lc appleetcode.cn id1971 langcpp** [1971] 寻找图中是否存在路径*/// lc codestart class UnionFind {vector&…...

程序可以创建多少个用户界面对象?
有人提到这样一个问题:”一个程序最多可以注册多少个窗口类?” 问题的答案不是一个具体的数字。因为大多数用户界面对象都来自一个共享的内存池,我们称之为”桌面堆内存”。尽管我们可以计算一个最大的理论值,但是在实际的场景中࿰…...

业绩不俗,毛利率下滑,股价接连下跌,片仔癀将向何处去?
撰稿|行星 来源|贝多财经 10月16日,中药龙头企业漳州片仔癀药业股份有限公司(600436.SH,下称“片仔癀”)发布截至9月30日的2023年前三季度业绩报告。发布财报后,片仔癀的股价多日下跌。 10月17日、18日、19日和20日…...

云安全—docker容器镜像检测
0x00 前言 docker镜像是属于整个云原生的重要基石之一,如果从镜像开始就没有安全性的话,那么整个云原生也就没有任何的安全性可言。所以镜像检测技术就成为了一个比较重要的点,本篇将通过研究docker镜像工具来整体分析风险以及应对方案。 市…...
JDBC相关记录
JDBC:Java DadaBase Connectivity 即Java语言连接数据库。 本质:JDBC是SUN公司制定的一套接口(interface)。 作用:不同的数据库有自己独特设计原理,JDBC的可以让Java程序员关注业务本身,而不需要…...
Nginx的基本介绍 安装 配置文件 日志
一、Nginx介绍二、nginx的优点三、多路复用1、I/O multiplexing 多并发 四、nginx内部技术架构五、安装NginxNginx部署-yum安装获取Nginx的yum源yum安装Nginx浏览器访问 编译安装Nginx安装编译环境安装依赖环境创建nginx用户安装nginx启动nginx实现nginx开机自启(脚…...

docker部署nginx并设置挂载
前言: 最近在学习docker和nginx,因为容器在运行过程中,相关的配置文件及日志都会存在容器内。对容器以来较高,当容器不存在的时候。所有的文件也就都没有了。并且当需要查看日志,修改配置文件的时候必须进入到容器内部…...
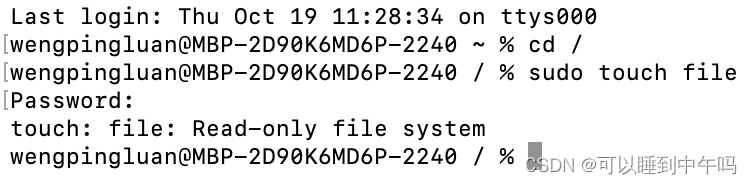
MAC如何在根目录创建文件
在这之前先明确一下啥是根目录。 打开终端,输入cd /,然后输入 ls 查看根目录下有哪些文件 可以看到 usr、etc、opt 这些文件的地方才叫根目录,而不是以用户命名,可以看到音乐、应用程序、影片、桌面的地方哈 介绍一种叫做软连接…...
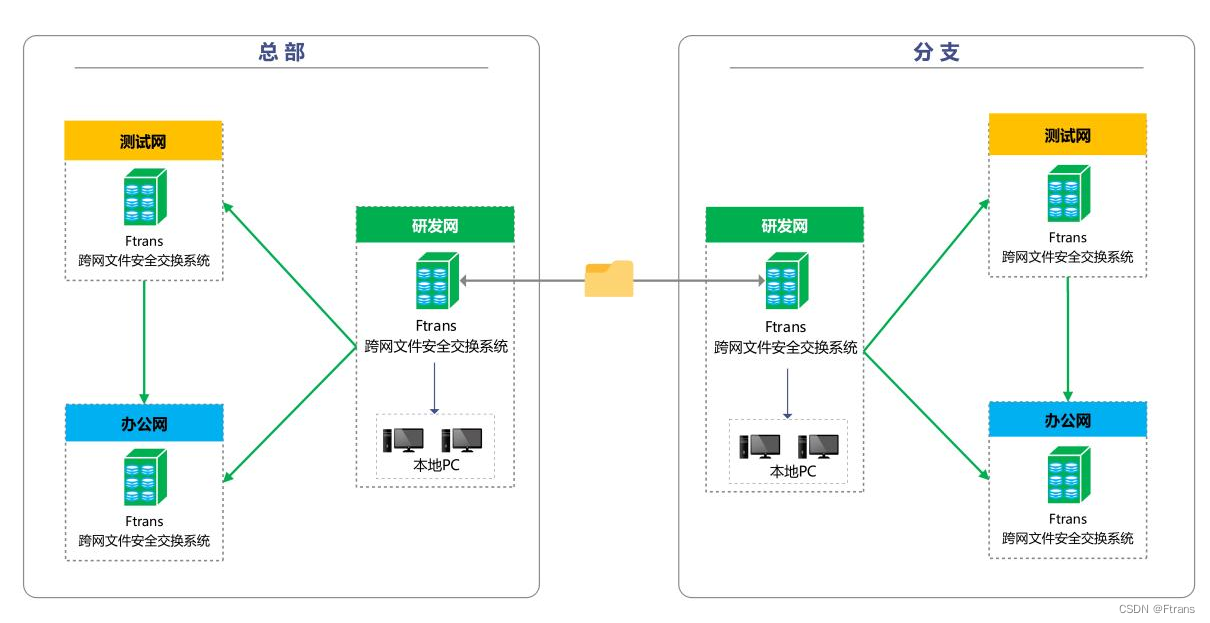
某全球领先的芯片供应商:优化数据跨网交换流程,提高安全管控能力
1、客户介绍 某全球领先的芯片供应商,成立于2005年,总部设于北京,在国内上海、深圳、合肥等地及国外多个国家和地区均设有分支机构和办事处,致力于为客户提供更优质、便捷的服务。 2、建设背景 该公司基于网络安全管理的需求&am…...

自然语言处理---文本预处理概述
自然语言处理(Natural Language Processing,简称NLP)是计算机科学与语言学中关注于计算机与人类语言间转换的领域。其主要应用于:语音助手、机器翻译、搜索引擎、智能问答等。 文本预处理概述 文本语料在输送给模型前一般需要一…...

GCC编译器 什么是宏? 标识符和关键字
一.GCC是什么? GCC是用于编译C语言和其它语言的开源软件。 全称是 GNU Compiler Collection,意思是GNU编译器集和。 支持多种操作系统和硬件平台。二.GCC的作用 GCC的作用是将源码转换为可执行的文件,使之可以在计算机上运行。三.GCC编译c文…...
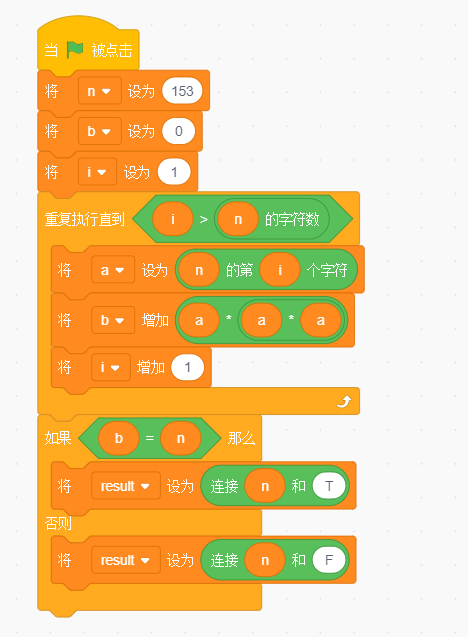
【GESP】2023年06月图形化三级 -- 自幂数判断
文章目录 自幂数判断【题目描述】【输入描述】【输出描述】【参考答案】其他测试用例 自幂数判断 【题目描述】 自幂数是指N位数各位数字N次方之和是本身,如153是3位数,其每位数的3次方之和是153本身,因此153是自幂数,1634是4位数…...

MySQL常见面试题
一、存储引擎相关 (1)MySQL 支持哪些存储引擎? MySQL支持多种存储引擎,比如InnoDB,MyISAM, MySQL大于等于5.5之后,默认存储引擎是InnoDB (2)InnoDB 和 MyISAM 有什么区别? InnoD…...

前端HTML CSS JS风格规范
本文代码规范来自HTML/CSS代码开发规范文档 文件命名规范 使用小写字母、数字和下划线组成文件名。 避免使用特殊字符和空格。 使用语义化的命名,能够清晰地表达出文件的功能或内容。 目录结构规范 使用约定俗成的目录结构,如:src/compon…...
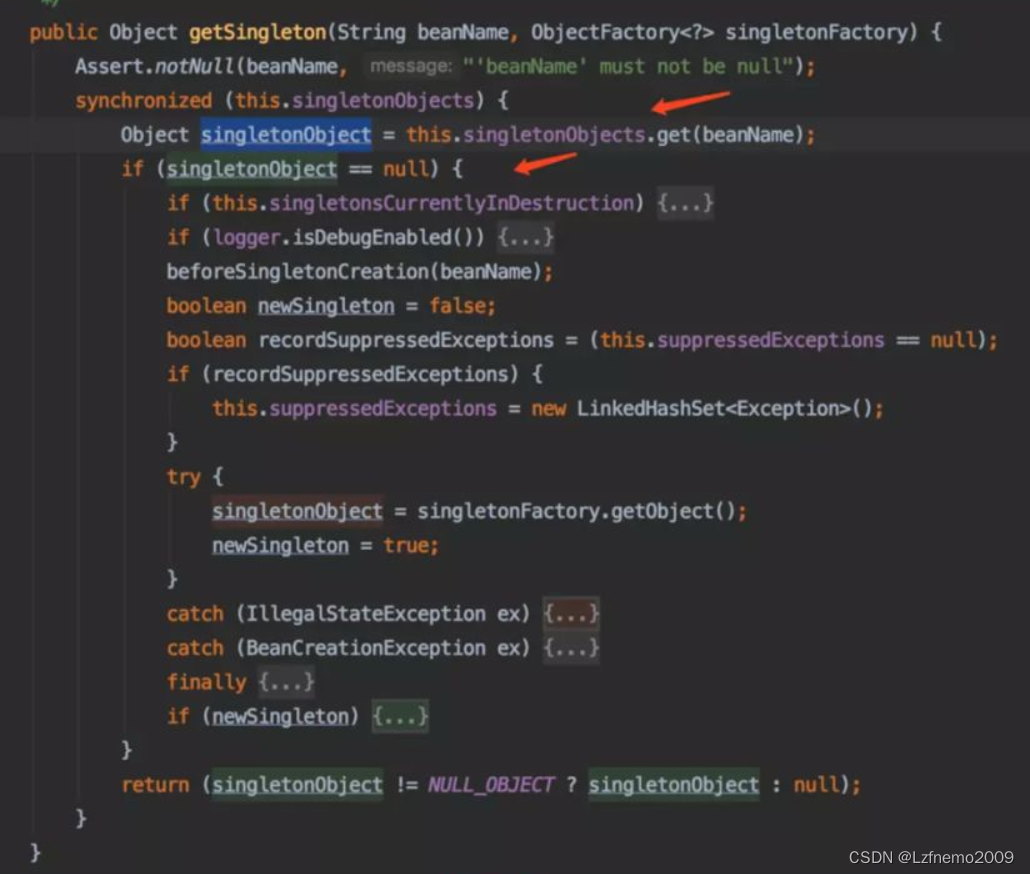
为什么spring默认采用单例bean
概 述 熟悉 Spring开发的朋友都知道 Spring 提供了 5种 scope,分别是: singleton: 单例模式,当spring创建applicationContext容器的时候,spring会欲初始化所有的该作用域实例,加上lazy-init就可以避免预处理…...

Redisson分布式锁学习
之前工作中一直使用redis来实现分布式锁,但是最近项目使用了云弹性,机器会涉及到扩缩容,涉及到优雅停机的问题,普通的redis分布锁,一般使用时会设置锁的时间,但是如果在加锁期间 JVM异常重启等发生会导致分…...
Metabase:简单快捷的商业智能与数据分析工具 | 开源日报 No.61
moby/moby Stars: 66.8k License: Apache-2.0 Moby 是一个由 Docker 创建的开源项目,旨在实现和加速软件容器化。它提供了工具包组件的“乐高集”,可以将它们组装成基于容器的自定义系统的框架。组件包括容器生成工具、容器注册表、业务流程工具、运行时…...

【无标题】高流量大并发Linux TCP性能调优
最近在使用jmeter做压测,当jmeter的并发量高的时候发现jmeter服务器一直报错Cannot assign requested address, 查看了一下发现系统中存在大量处于TIME_WAIT状态的tcp端口 netstat -n | awk ‘/^tcp/ {S[$NF]} END {for(a in S) print a, S[a]}’ TIME_W…...

优雅的用户体验:微信小程序中的多步骤表单引导
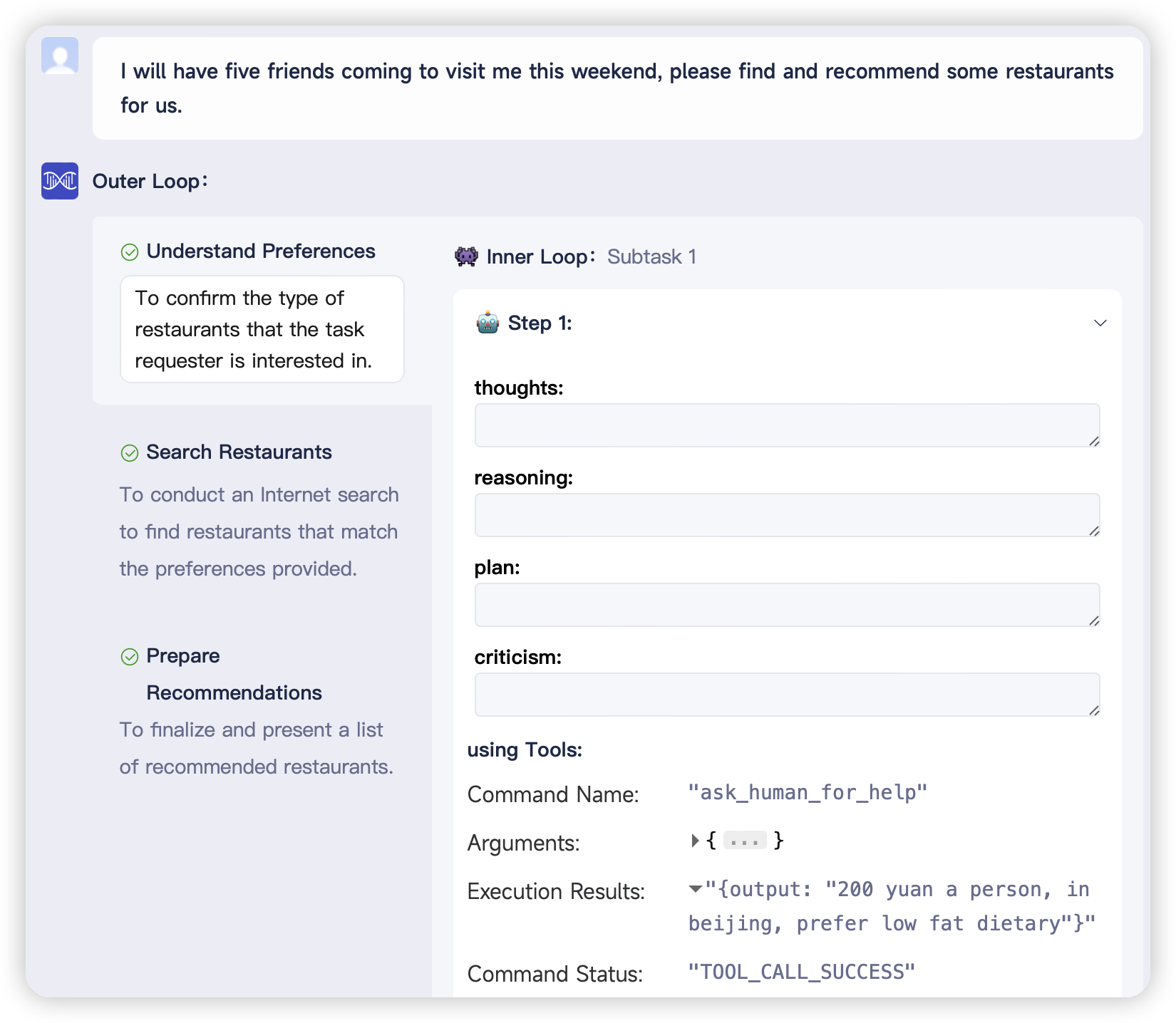
前言 在微信小程序中,实现一个多步骤表单引导界面既可以提供清晰的任务指引,又可以增加用户体验的互动性。本文将探讨如何使用微信小程序的特性,构建一个流程引导界面,帮助用户一步步完成复杂任务。我们将从设计布局和样式开始&am…...

Kotlin中的委托、属性委托和延迟加载
委托模式是一种常用的设计模式,用于将某个对象的责任委托给另一个对象来处理。在Kotlin中,委托可以通过关键字by来实现,主要分为类委托和属性委托两种形式。此外,Kotlin还提供了延迟加载的功能,可以在需要时才进行初始…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...

使用VMware克隆功能快速搭建集群
自己搭建的虚拟机,后续不管是学习java还是大数据,都需要集群,java需要分布式的微服务,大数据Hadoop的计算集群,如果从头开始搭建虚拟机会比较费时费力,这里分享一下如何使用克隆功能快速搭建一个集群 先把…...
