线性代数相关笔记
线性基
导入
线性基,顾名思义,就是一个包含数字最少的集合,使得原集合中的任何数都能用线性基中的元素表示。
集合中的元素满足一些性质:
- 原集合中的任意元素都可以用线性基中的若干元素的异或和表示
- 线性基中任意数异或和不为 0 0 0,否则不满足集合大小最小
- 以任意顺序枚举原集合中元素,所得集合大小相同
- 大小为 n n n 的线性基可以表示 2 n 2^n 2n 个数;若线性基中存在二进制第 i i i 位为 1 1 1 的数,则可以表示 2 n − 1 2^{n-1} 2n−1 个二进制下第 i i i 位为 1 1 1 的数。
操作
插入
我们用数组 p 表示线性基,假设要插入 x x x,从高到低枚举 x x x 的二进制的每一位数字,如果 x x x 的第 i i i 位为 1 1 1 且 p i = 0 p_i=0 pi=0,那么令 p i = x p_i=x pi=x 并结束插入;否则,令 x^=p[i],继续枚举下一位。
void insert(int x)
{for(int i=50;i>=0;--i)if(x>>i&1){if(!p[i]) {p[i]=x;break;}else x^=p[i];}
}
求异或最大值
求原集合的子集的异或最大值,利用贪心思想。若 ans^p[i]>ans,则 ans^=p[i]。
int pmax()
{int ans=0;for(int i=50;i>=0;--i)if((ans^p[i])>ans) ans^=p[i];return ans;
}
求异或最小值
分两种情况考虑:
- 线性基大小 < < < 原集合大小:原集合中一定存在异或和为 0 0 0 的一些数,所以异或最小值为 0 0 0。
- 线性基大小 = = = 原集合大小:在线性基内求异或最小值,线性基内的最小元素与其他元素异或得到的值一定更大,所以异或最小值为线性基中最小元素。
剩的异或 k k k 小值先咕了 QwQ
本来学线性基是想过 YbtOJ 的最大异或对的,结果发现线性基是任意数的最大异或和,这一道题是一对,只能用 trie 树
练手板子题
代码如下:
#include <bits/stdc++.h>
using namespace std;
#define int long longint p[55];void insert(int x)
{for(int i=50;i>=0;--i)if(x>>i&1){if(!p[i]) {p[i]=x;break;}else x^=p[i];}
}int pmax()
{int ans=0;for(int i=50;i>=0;--i)if((ans^p[i])>ans) ans^=p[i];return ans;
}signed main()
{int n,x;cin>>n;for(int i=1;i<=n;i++) cin>>x,insert(x);cout<<pmax();return 0;
}
行列式
行列式,是一种对于矩阵的特殊形式——方阵的表示形式。所谓方阵,就是 n × n n\times n n×n的矩阵。
一个 n × n n\times n n×n 的方阵 A A A 的行列式记为 det ( A ) \det(A) det(A) 或者 ∣ A ∣ |A| ∣A∣,一个 2 × 2 2\times2 2×2 矩阵的行列式可表示如下:
det ( a b c d ) = a d − b c \det \begin{pmatrix} a&b\\ c&d \end{pmatrix}=ad-bc det(acbd)=ad−bc
把一个 n n n 阶行列式中的元素 a i j a_{ij} aij 所在的第 i i i行和第 j j j列划去后,留下来的 n − 1 n-1 n−1 阶行列式叫做元素 a i j a_{ij} aij 的余子式,记作 M i j M_{ij} Mij。记 A i j = ( − 1 ) i + j M i j A_{ij}=(-1)^{i+j}M_{ij} Aij=(−1)i+jMij,叫做元素 a i j a_{ij} aij 的代数余子式。
一个 n × n n\times n n×n 矩阵的行列式等于其任意行(或列)的元素与对应的代数余子式乘积之和,即:
det ( A ) = a i 1 A i 1 + ⋯ + a i n + A i n = ∑ j = 1 n a i j ( − 1 ) i + j det ( A i j ) \det(A)=a_{i1}A_{i1}+\cdots+a_{in}+A_{in}=\sum_{j=1}^na_{ij}(-1)^{i+j}\det(A_{ij}) det(A)=ai1Ai1+⋯+ain+Ain=j=1∑naij(−1)i+jdet(Aij)
代码实现:
int dett(int a[maxn][maxn],int n)//n为阶数
{int dett=0,k=0,h=0;if(n==1) return a[0][0];else if(n==2) return a[0][0]*a[1][1]-a[0][1]*a[1][0];else{for(int p=0;p<n;p++){for(int i=0;i<n;i++)for(int j=0;j<n;j++){if(j==p) continue;tmp[h][k]=a[i][j],k++;if(k==n-1) h++,k=0;}dett=dett+a[0][p]*pow(-1,p)*det(tmp,n-1)}return dett;}
}
高斯消元
前置芝士
三角矩阵
上三角矩阵的对角线左下方的系数全部为 0 0 0,下三角矩阵的对角线右上方的系数全部为 0 0 0。三角矩阵可以看作是一般方阵的一种简化情形。由于带三角矩阵的矩阵方程容易求解,在解多元线性方程组时,总是将其系数矩阵通过初等变换化为三角矩阵来求解。
举个栗子,下面的矩阵 U U U 就是一个上三角矩阵。
U = [ u 1 , 1 u 1 , 2 u 1 , 3 ⋯ u 1 , n 0 u 2 , 2 u 2 , 3 ⋯ u 2 , n 0 0 ⋱ ⋱ ⋮ ⋮ ⋮ 0 ⋱ u n − 1 , n 0 0 ⋯ 0 u n , n ] U= \begin{bmatrix} u_{1,1}&u_{1,2}&u_{1,3}&\cdots&u_{1,n}\\ 0&u_{2,2}&u_{2,3}&\cdots&u_{2,n}\\ 0&0&\ddots&\ddots&\vdots\\ \vdots&\vdots&0&\ddots&u_{n-1,n}\\ 0&0&\cdots&0&u_{n,n} \end{bmatrix} U= u1,100⋮0u1,2u2,20⋮0u1,3u2,3⋱0⋯⋯⋯⋱⋱0u1,nu2,n⋮un−1,nun,n
增广矩阵
又称扩增矩阵,就是在系数矩阵的右边添上一列,这一列是线性方程组的等号右边的值。
高斯消元
基本思想
通过一系列的加减消元运算,将方程组化为上三角矩阵。然后再逐一回代求出 x x x。
实现过程
解方程:
{ 3 x 1 + 2 x 2 + x 3 = 6 2 x 1 + 2 x 2 + 2 x 3 = 4 4 x 1 − 2 x 2 − 2 x 3 = 2 \begin{cases} 3x_1+2x_2+x_3=6\\ 2x_1+2x_2+2x_3=4\\ 4x_1-2x_2-2x_3=2 \end{cases} ⎩ ⎨ ⎧3x1+2x2+x3=62x1+2x2+2x3=44x1−2x2−2x3=2
我们把这个方程组写成增广矩阵的形式:
相关文章:

线性代数相关笔记
线性基 导入 线性基,顾名思义,就是一个包含数字最少的集合,使得原集合中的任何数都能用线性基中的元素表示。 集合中的元素满足一些性质: 原集合中的任意元素都可以用线性基中的若干元素的异或和表示线性基中任意数异或和不为…...
】69 - Android 侧添加支持 busybox telnetd 服务)
【SA8295P 源码分析 (四)】69 - Android 侧添加支持 busybox telnetd 服务
【SA8295P 源码分析】69 - Android 侧添加支持 busybox telnetd 服务 一、下载 busybox-1.36.1.tar.bz2 源码包二、编译 busybox 源码三、将编译后的 busybox 打包编入Android 镜像中系列文章汇总见:《【SA8295P 源码分析 (四)】网络模块 文章链接汇总 - 持续更新中》 本文链接…...
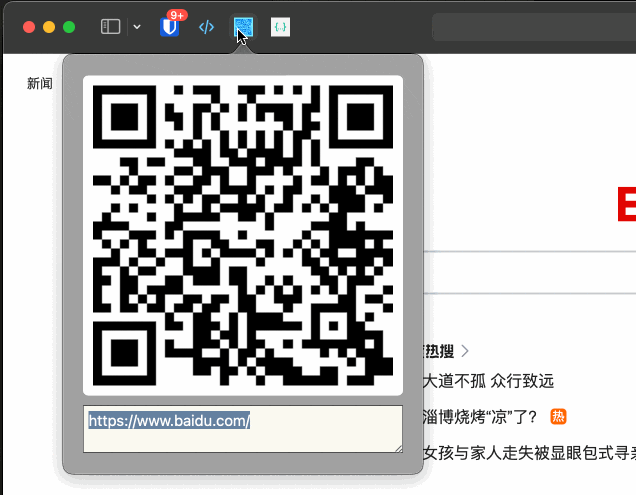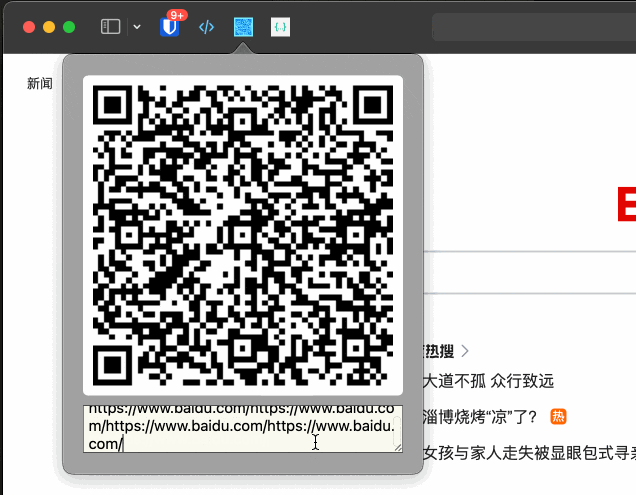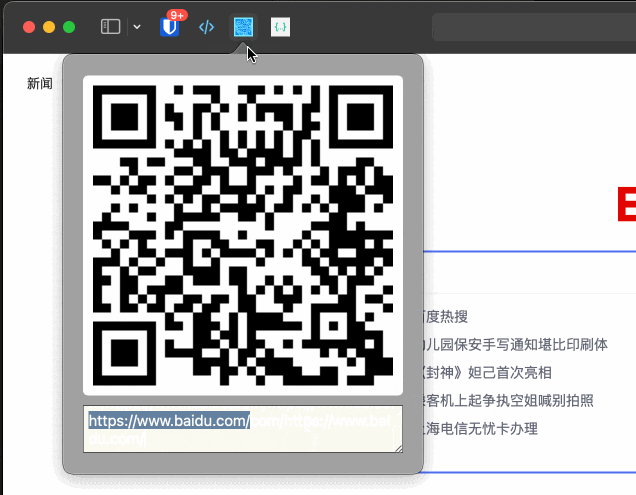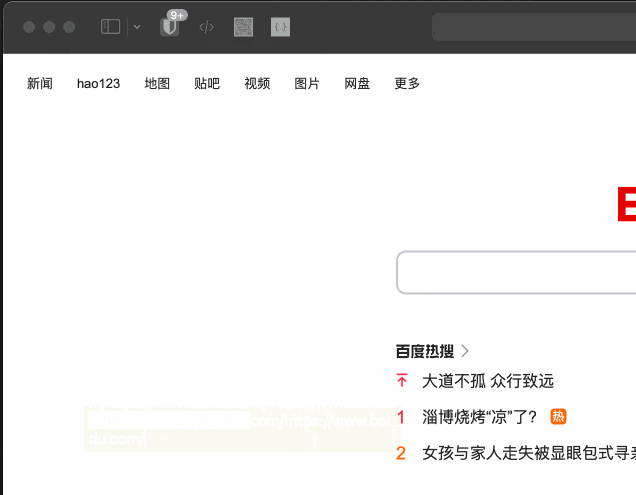
如何开发一个 Safari 插件
本文字数:2493字 预计阅读时间:15分钟 由于常用浏览器是Safari,而Safari浏览器的插件比不上Chrome,所以就有了自己开发常用的Safari插件的想法。 打算开发当前页面生成二维码的Extension,因为网络原因,AirD…...

n皇后问题,不用递归
注释如下: class Solution:def totalNQueens(self, n: int) -> int:if n < 1: # 如果 n 小于 1,直接返回 0return 0count 0 # 初始化解的个数为 0stack [(0, set(), set(), set())] # 初始化一个栈,元素为当前处理的行数、已经放…...
Verilog基础:$fopen和$fclose系统函数、任务的使用
相关阅读 Verilog基础https://blog.csdn.net/weixin_45791458/category_12263729.html?spm1001.2014.3001.5482 $fopen和$fclose是两个用于打开和关闭文件的系统函数、任务。最初,在Verilog-1995标准中,最多只能同时打开32个文件,其所使用的…...

python之字典的用法
python之字典的用法 Python中的字典是一种无序、可变、可迭代的数据类型,它由键值对组成,每个键都映射到一个值。字典在Python中被视为可变对象,这意味着我们可以随时更新、添加或删除字典中的键值对。 以下是一些关于Python字典的基本用法&a…...
Leetcode1971. 寻找图中是否存在路径
Every day a Leetcode 题目来源:1971. 寻找图中是否存在路径 解法1:并查集 并查集介绍:并查集详解 代码: /** lc appleetcode.cn id1971 langcpp** [1971] 寻找图中是否存在路径*/// lc codestart class UnionFind {vector&…...

程序可以创建多少个用户界面对象?
有人提到这样一个问题:”一个程序最多可以注册多少个窗口类?” 问题的答案不是一个具体的数字。因为大多数用户界面对象都来自一个共享的内存池,我们称之为”桌面堆内存”。尽管我们可以计算一个最大的理论值,但是在实际的场景中࿰…...

业绩不俗,毛利率下滑,股价接连下跌,片仔癀将向何处去?
撰稿|行星 来源|贝多财经 10月16日,中药龙头企业漳州片仔癀药业股份有限公司(600436.SH,下称“片仔癀”)发布截至9月30日的2023年前三季度业绩报告。发布财报后,片仔癀的股价多日下跌。 10月17日、18日、19日和20日…...

云安全—docker容器镜像检测
0x00 前言 docker镜像是属于整个云原生的重要基石之一,如果从镜像开始就没有安全性的话,那么整个云原生也就没有任何的安全性可言。所以镜像检测技术就成为了一个比较重要的点,本篇将通过研究docker镜像工具来整体分析风险以及应对方案。 市…...
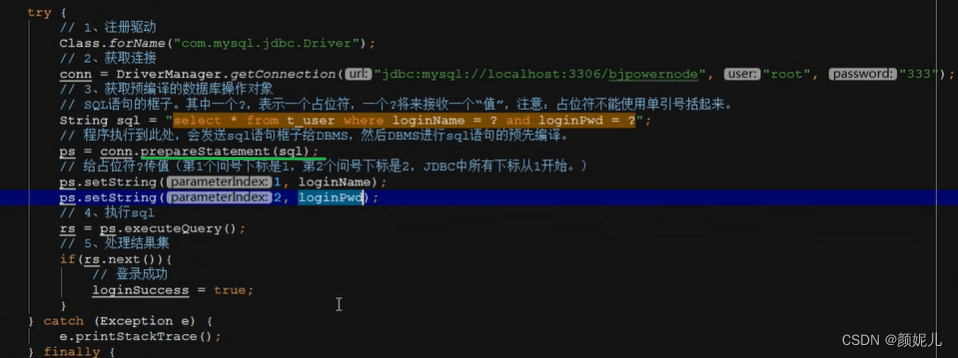
JDBC相关记录
JDBC:Java DadaBase Connectivity 即Java语言连接数据库。 本质:JDBC是SUN公司制定的一套接口(interface)。 作用:不同的数据库有自己独特设计原理,JDBC的可以让Java程序员关注业务本身,而不需要…...
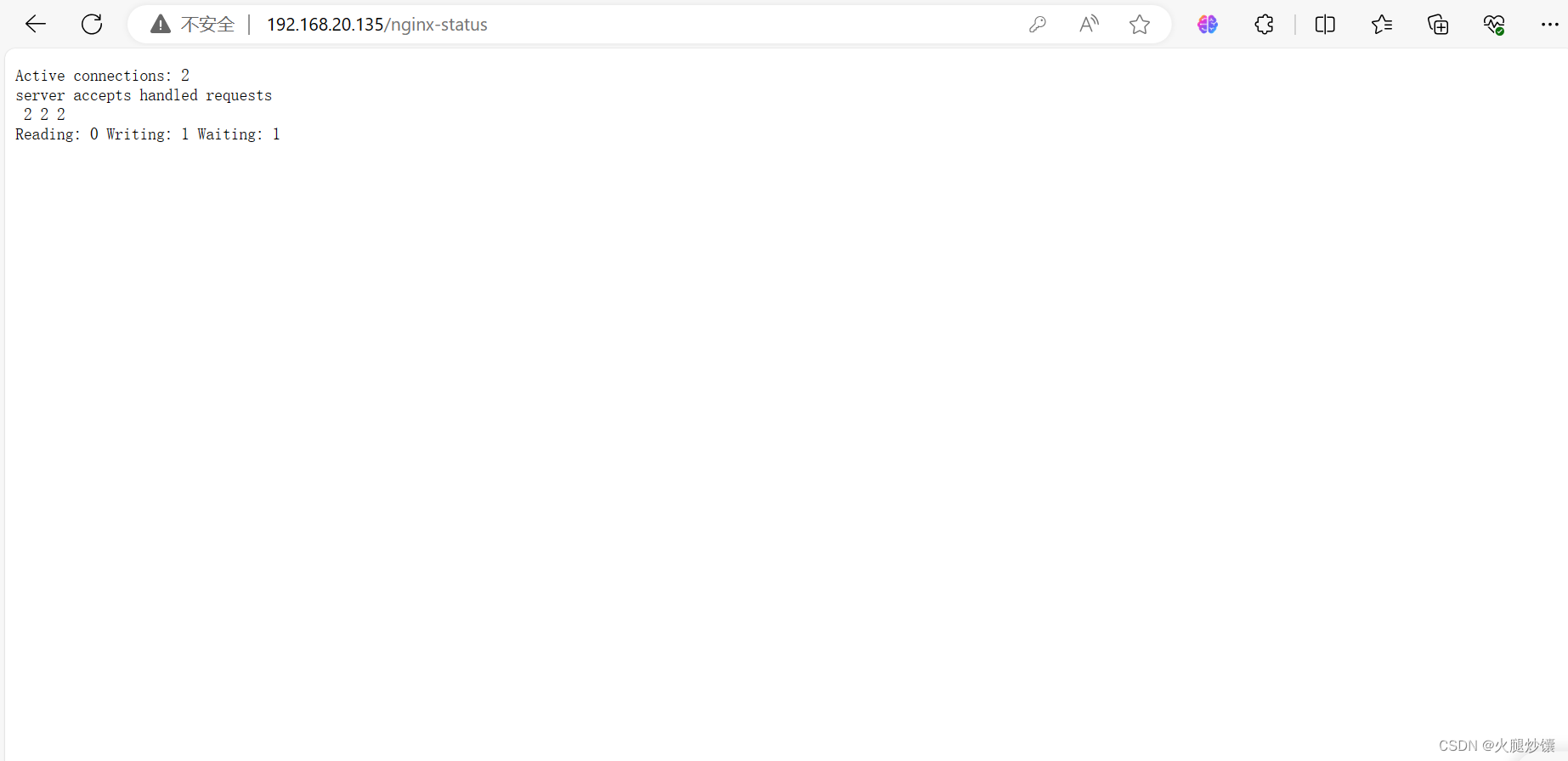
Nginx的基本介绍 安装 配置文件 日志
一、Nginx介绍二、nginx的优点三、多路复用1、I/O multiplexing 多并发 四、nginx内部技术架构五、安装NginxNginx部署-yum安装获取Nginx的yum源yum安装Nginx浏览器访问 编译安装Nginx安装编译环境安装依赖环境创建nginx用户安装nginx启动nginx实现nginx开机自启(脚…...

docker部署nginx并设置挂载
前言: 最近在学习docker和nginx,因为容器在运行过程中,相关的配置文件及日志都会存在容器内。对容器以来较高,当容器不存在的时候。所有的文件也就都没有了。并且当需要查看日志,修改配置文件的时候必须进入到容器内部…...
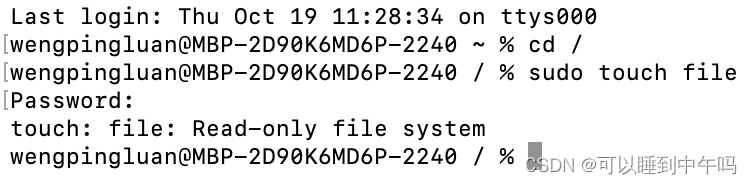
MAC如何在根目录创建文件
在这之前先明确一下啥是根目录。 打开终端,输入cd /,然后输入 ls 查看根目录下有哪些文件 可以看到 usr、etc、opt 这些文件的地方才叫根目录,而不是以用户命名,可以看到音乐、应用程序、影片、桌面的地方哈 介绍一种叫做软连接…...
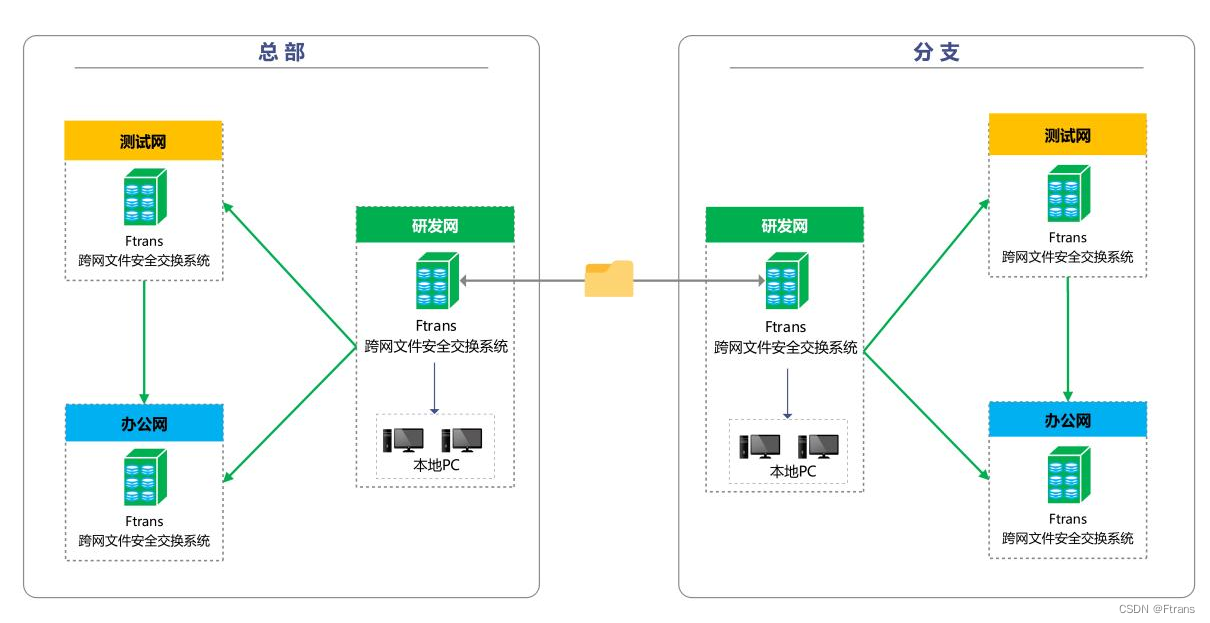
某全球领先的芯片供应商:优化数据跨网交换流程,提高安全管控能力
1、客户介绍 某全球领先的芯片供应商,成立于2005年,总部设于北京,在国内上海、深圳、合肥等地及国外多个国家和地区均设有分支机构和办事处,致力于为客户提供更优质、便捷的服务。 2、建设背景 该公司基于网络安全管理的需求&am…...

自然语言处理---文本预处理概述
自然语言处理(Natural Language Processing,简称NLP)是计算机科学与语言学中关注于计算机与人类语言间转换的领域。其主要应用于:语音助手、机器翻译、搜索引擎、智能问答等。 文本预处理概述 文本语料在输送给模型前一般需要一…...

GCC编译器 什么是宏? 标识符和关键字
一.GCC是什么? GCC是用于编译C语言和其它语言的开源软件。 全称是 GNU Compiler Collection,意思是GNU编译器集和。 支持多种操作系统和硬件平台。二.GCC的作用 GCC的作用是将源码转换为可执行的文件,使之可以在计算机上运行。三.GCC编译c文…...
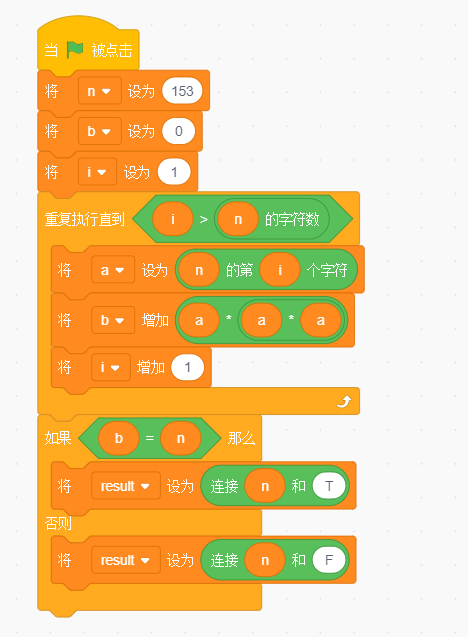
【GESP】2023年06月图形化三级 -- 自幂数判断
文章目录 自幂数判断【题目描述】【输入描述】【输出描述】【参考答案】其他测试用例 自幂数判断 【题目描述】 自幂数是指N位数各位数字N次方之和是本身,如153是3位数,其每位数的3次方之和是153本身,因此153是自幂数,1634是4位数…...

MySQL常见面试题
一、存储引擎相关 (1)MySQL 支持哪些存储引擎? MySQL支持多种存储引擎,比如InnoDB,MyISAM, MySQL大于等于5.5之后,默认存储引擎是InnoDB (2)InnoDB 和 MyISAM 有什么区别? InnoD…...

前端HTML CSS JS风格规范
本文代码规范来自HTML/CSS代码开发规范文档 文件命名规范 使用小写字母、数字和下划线组成文件名。 避免使用特殊字符和空格。 使用语义化的命名,能够清晰地表达出文件的功能或内容。 目录结构规范 使用约定俗成的目录结构,如:src/compon…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...
OPENCV图形计算面积、弧长API讲解(1)
一.OPENCV图形面积、弧长计算的API介绍 之前我们已经把图形轮廓的检测、画框等功能讲解了一遍。那今天我们主要结合轮廓检测的API去计算图形的面积,这些面积可以是矩形、圆形等等。图形面积计算和弧长计算常用于车辆识别、桥梁识别等重要功能,常用的API…...
