[C++随想录] 二叉搜索树
搜素二叉树
- 二叉搜索树的使用
- 二叉搜索树的模拟实现(K)
- 整体结构
- 循环版本
- 递归版本
- 二叉搜索树的应用
- 源码(kv)
二叉搜索树的使用
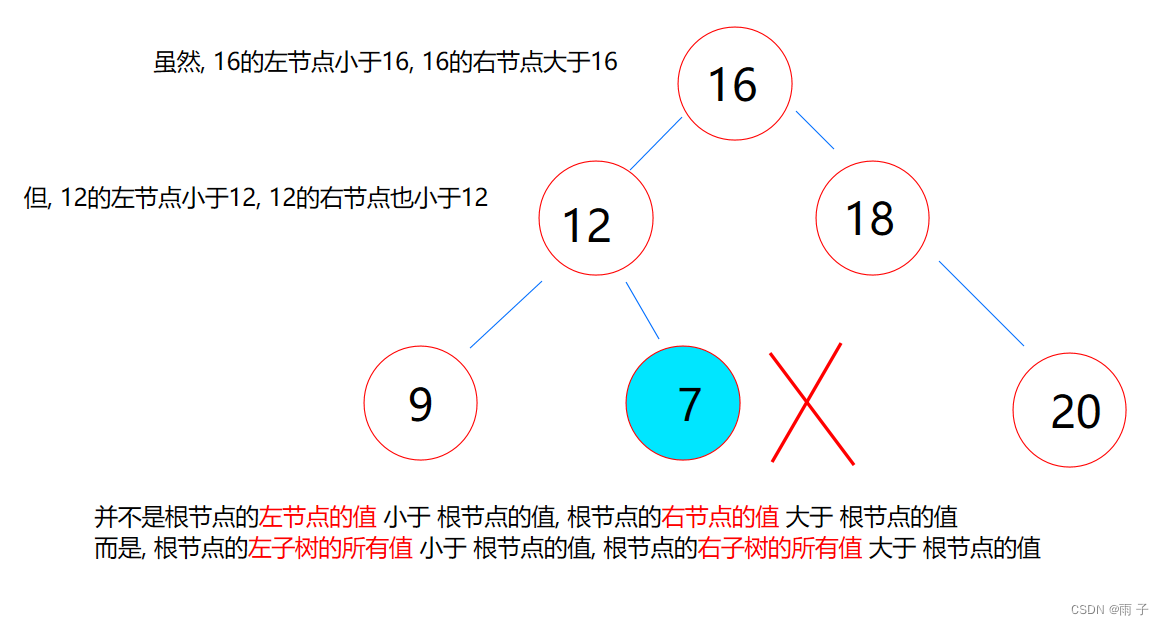
二叉搜索树 相较于 普通的二叉树来说:
- 根节点的左子树的所有键值都
小于根节点, 根节点的右子树的所有键值大于根节点 - 根节点的
左右子树 都是 二叉搜索树 中序遍历是升序的⇒ 二叉搜素树 又叫作二叉排序树
- 子树 && 节点
- 查找
假如查找 key, 有如下四种情况:- 如果 key
>根节点的值, 那么就去根节点的右子树去查找 - 如果 key
<根节点的值, 那么就去根节点的左子树去查找 - 如果 key
=根节点的值, 那么就找到了 - 如果找到
空, 那就不存在
- 如果 key
- 查找的时间复杂度是
O(高度次), 而不是O(logN)
如果是完全二叉树, 那么就是O(logN);如果退化到极限情况, 类似于链表, 那么就是O(N)

所以, 总结下来, 时间复杂度就是O(高度次)
那么如何解决这种退化问题呢? ⇒AVL树 和 红黑树 就是针对这种情况做了特殊处理 --> 旋转
-
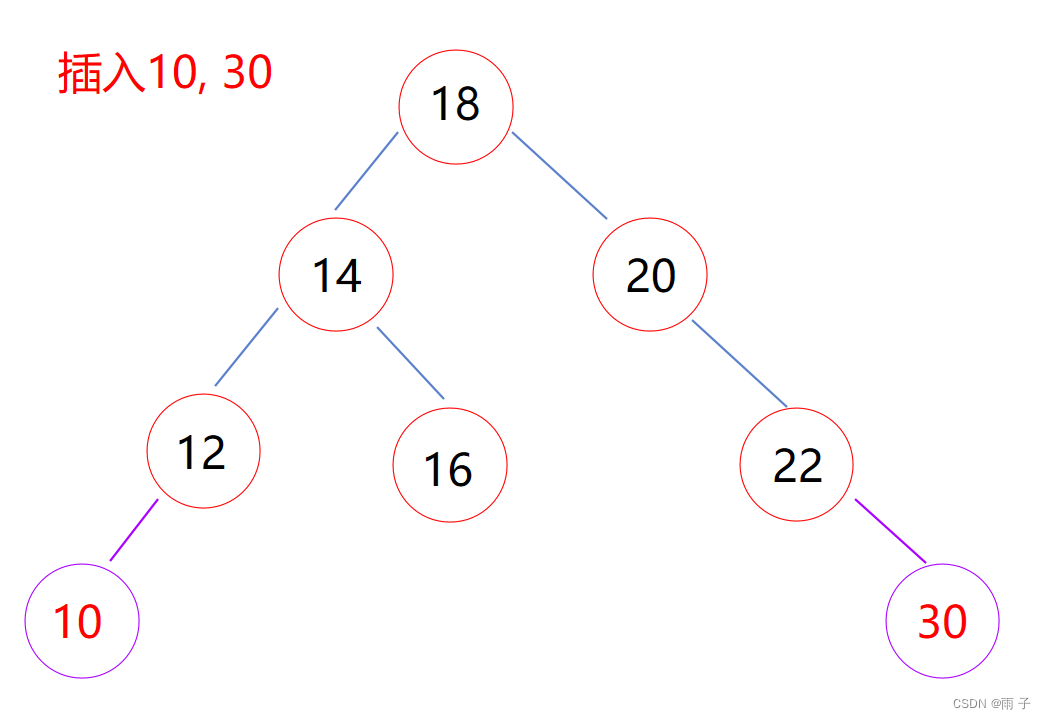
插入
总体思想:找到非空节点去插入
-
删除key
- 先找到key的位置, 有两种情况:
- 没找到, 那就直接返回
- 找到了key的位置, 记作cur. 找到了也有三种情况:
- cur的左子树为空
- cur的右子树为空
- cur的左右子树都不为空
- 先找到key的位置, 有两种情况:
由于 cur要进行删除, 要把cur后面的内容链接到parent的后面. && cur也有两种可能 parent的左子树 or 右子树 ⇒ 我们要cur后面的内容链接到 cur处于parent的位置
删除具体如下👇👇👇
- cur的右子树为空
(1) cur是parent的左子树
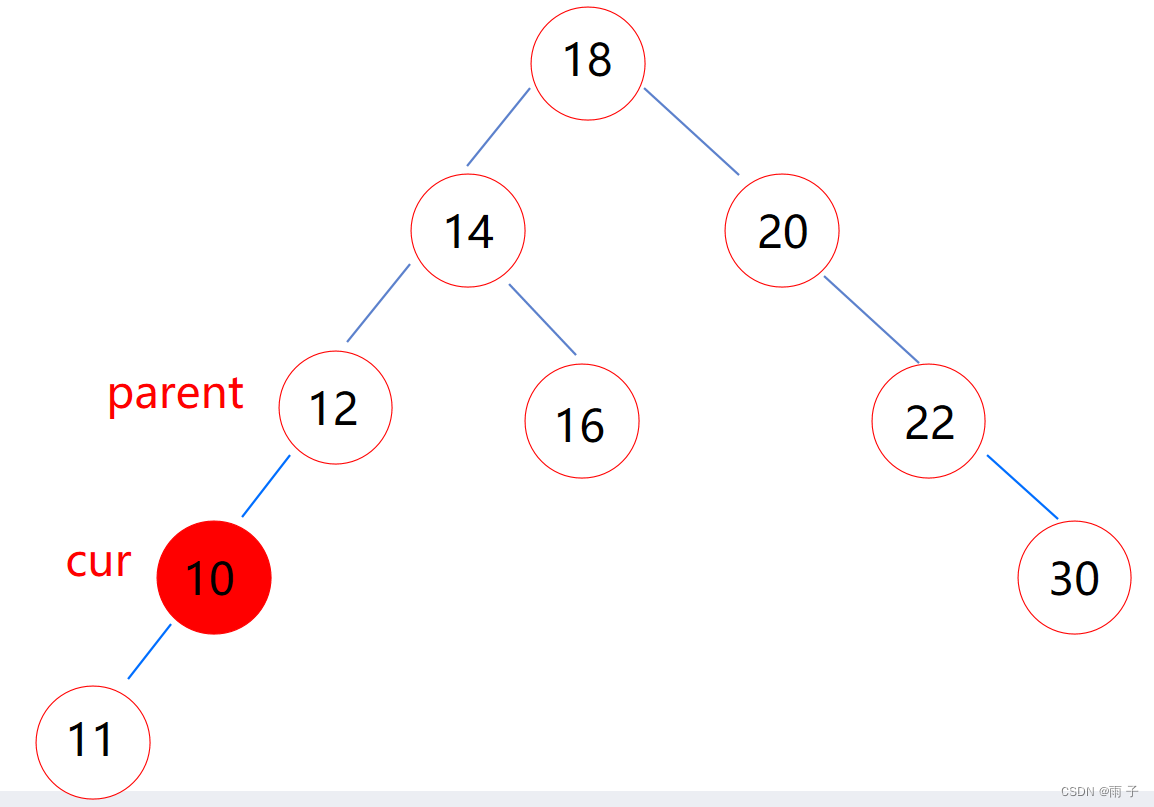
(2) cur是parent的右子树
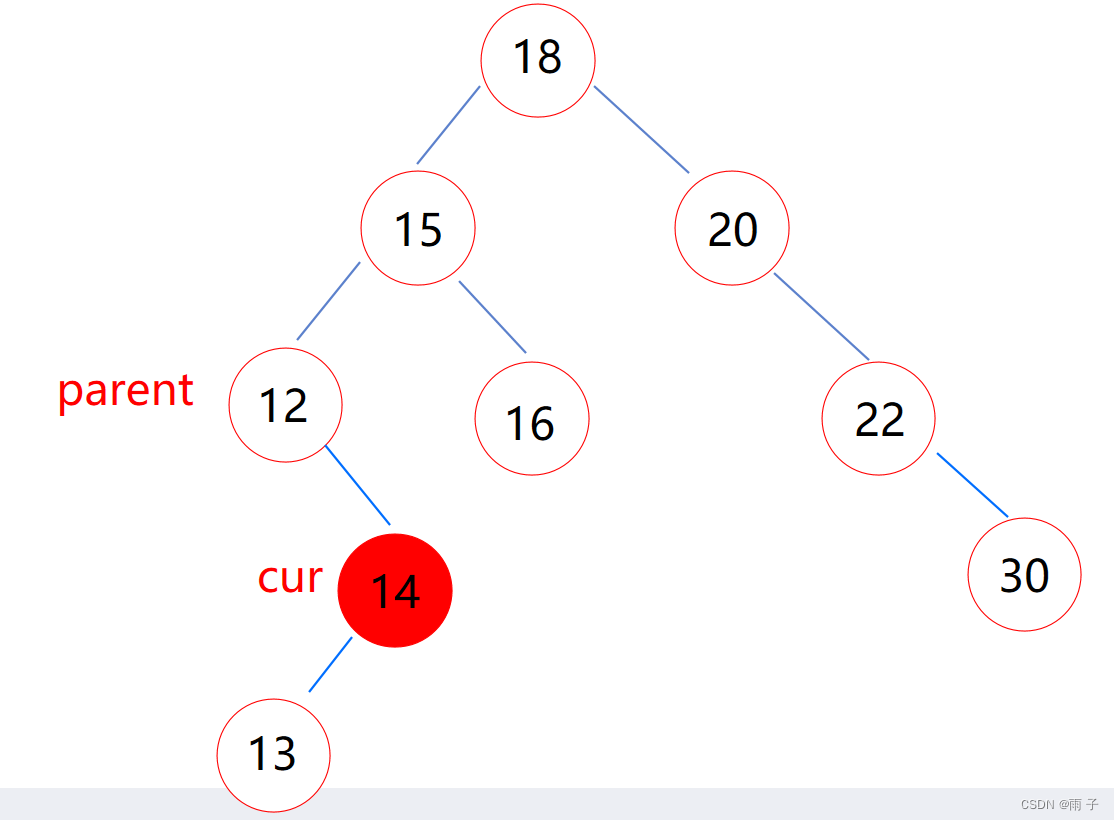
- cur的左子树为空
(1) cur是parent的左子树
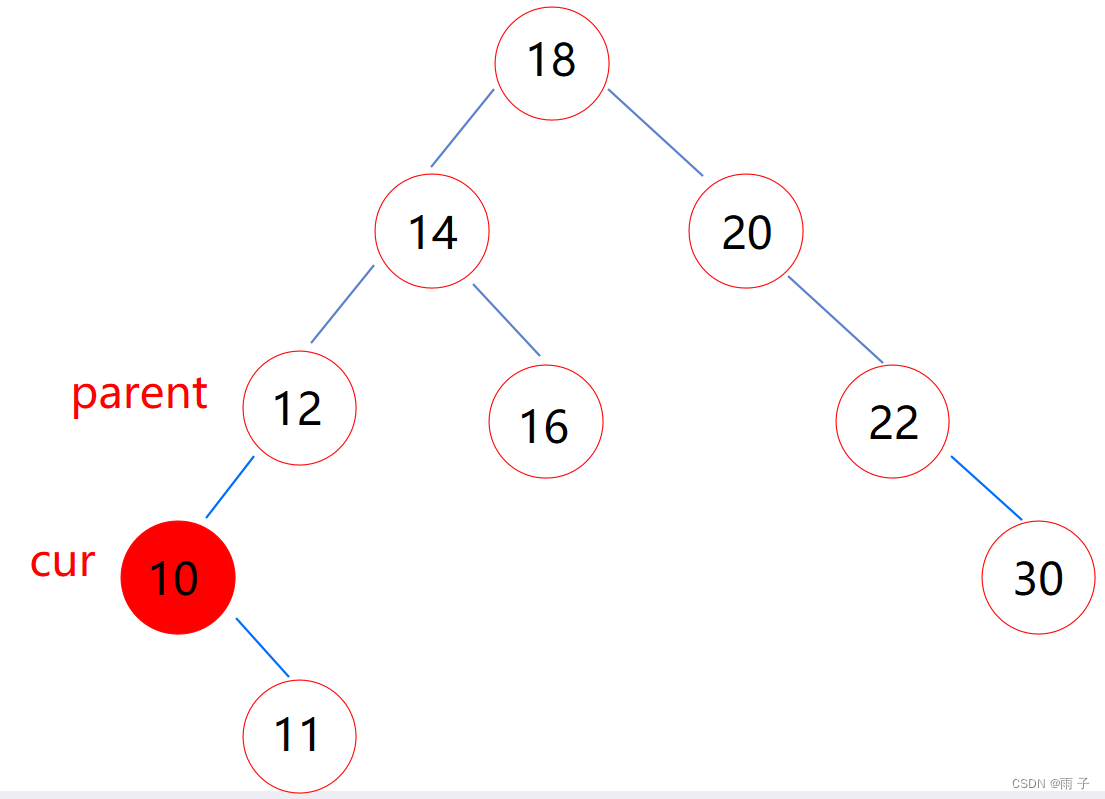
(2) cur是parent的右子树

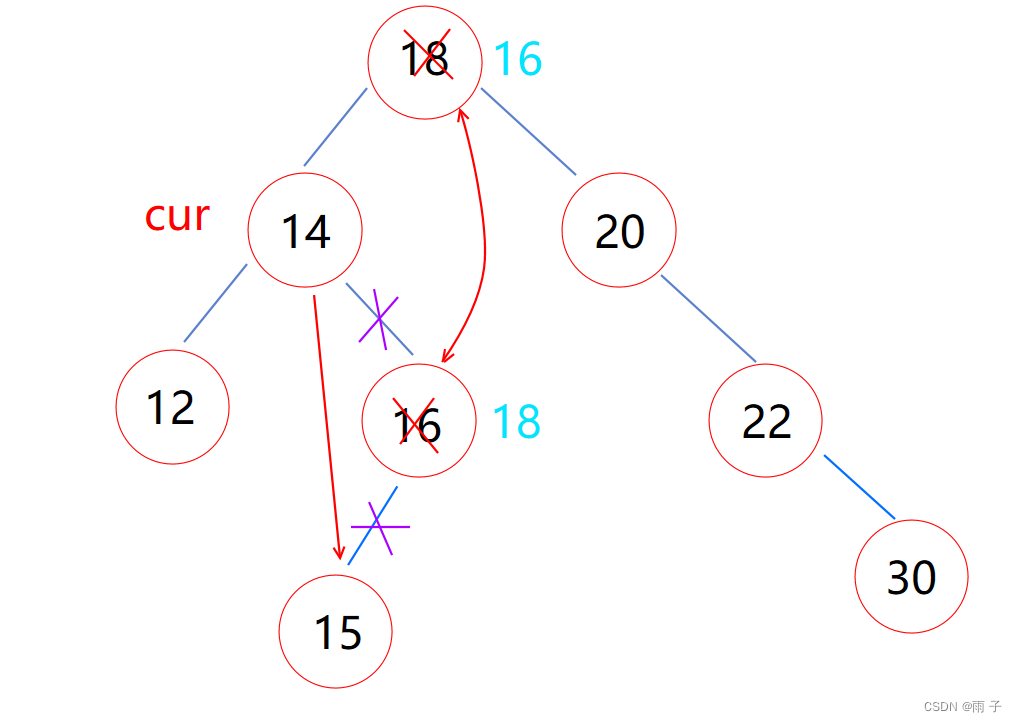
- cur的左右子树都不为空
🗨️删除掉cur, 那么我们如何链接cur的左右子树呢?-
可以找一个节点来替换掉cur, 然后我们来处理这个节点的链接关系就好了
🗨️替换过去, 也不改变二叉搜索树的结构, 那么节点是什么好呢? 后面集中处理这个节点, 那么这个节点应该容易处理才对, 那么这个节点是叶子节点吗? - 替换过去, 不改变二叉树的结构 — —
替换节点应该为 cur的左子树的最大节点 或者 cur的右子树的最小节点⇐中序遍历, cur旁边的两个数; 中序是 左跟右, ⇒ 那么就应该是左子树的最大节点, 或者右子树的最小节点
左子树的最大节点, 或者右子树的最小节点; 正好是叶子节点⇒ 那么我们处理这个替换节点也比较容易⇒ 思想同上替换节点的左子树为空, 或 替换节点的右子树为空
-
二叉搜索树的模拟实现(K)
整体结构
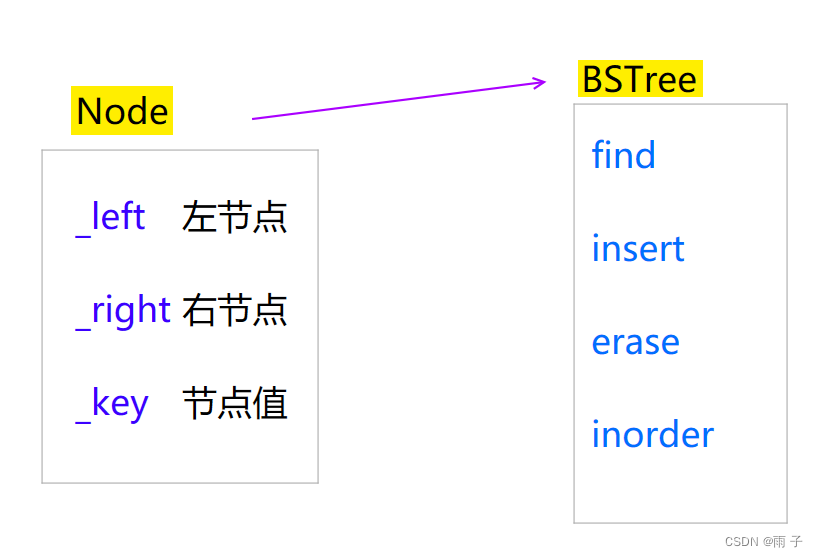
Node类
template<class T>struct BSTreeNode{public:BSTreeNode(const T& key):_left(nullptr),_right(nullptr),_key(key){}public:BSTreeNode<T>* _left;BSTreeNode<T>* _right;T _key;};
BSTree类
template<class T>
class BSTree
{typedef BSTreeNode<T> Node;
public:BSTree():_root(nullptr){}// 析构函数~BSTree(){_BSTree(_root);}private:// 析构函数void _BSTree(Node* root){if (root == nullptr)return;// 后序遍历进行删除_BSTree(root->_left);_BSTree(root->_right);delete root;}// 成员函数Node* _root;
}
循环版本
- find
Node* find(const K& key)
{return _find(_root, key);
}private:
Node* _find(Node* root, const T& key)
{Node* cur = root;while (cur){if (key > cur->_key){cur = cur->_right;}else if (key < cur->_key){cur = cur->_left;}else{return cur;}}return nullptr;
}
- insert
bool insert(const T& key)
{Node* newnode = new Node(key);if (_root == nullptr){_root = newnode;return true;}Node* parent = nullptr;Node* cur = _root;// 寻找插入的位置while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else{break;}}// 链接if (key > parent->_key){parent->_right = newnode;}else if (key < parent->_key){parent->_left = newnode;}else{return false;}return true;
}
- inorder
void Inorder()
{_Inorder(_root);
}private:
void _Inorder(Node* root)
{if (root == nullptr)return;_Inorder(root->_left);std::cout << root->_key << " ";_Inorder(root->_right);}
- erase

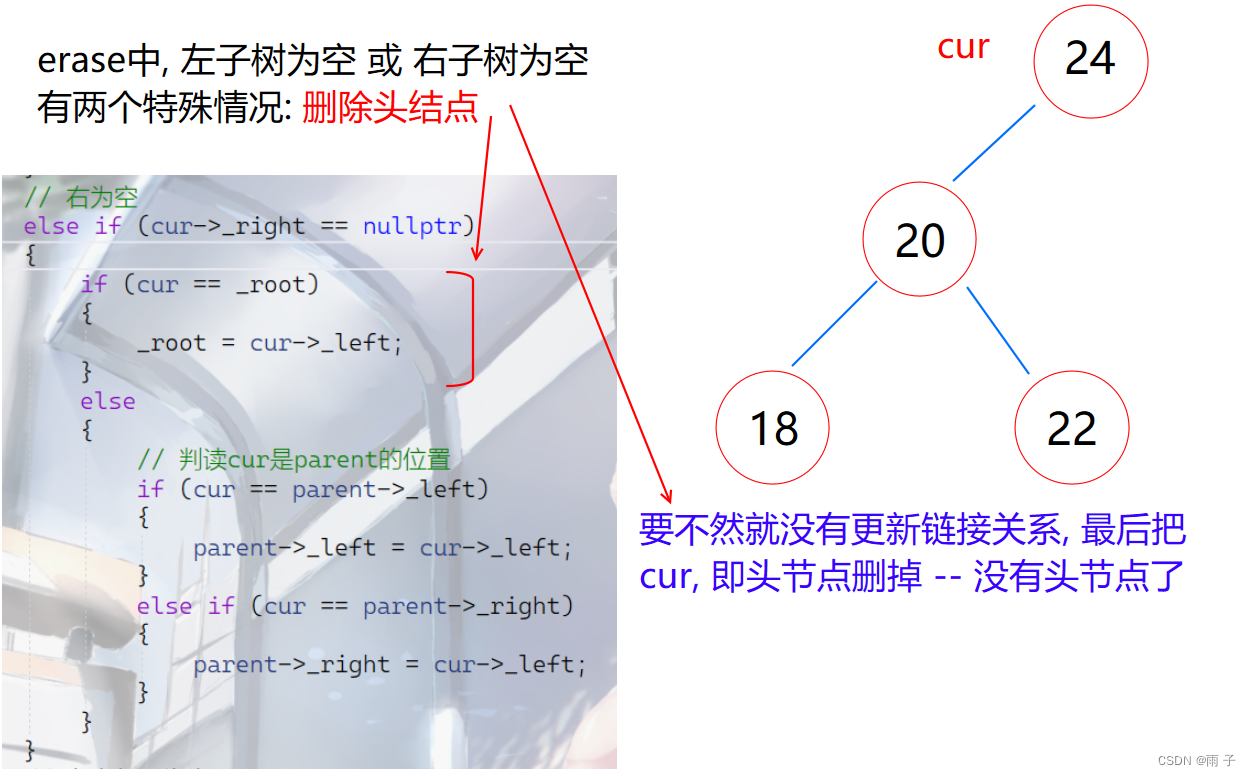
bool erase(const T& key)
{return _erase(_root, key);
}private:
bool _erase(Node* root, const T& key)
{// 先找到位置Node* parent = root;Node* cur = root;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;} else if (key < cur->_key){parent = cur;cur = cur->_left;}// 找到了else{// 左为空if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{// 判读cur是parent的位置if (cur == parent->_left){parent->_left = cur->_right;}else if (cur == parent->_right){parent->_right = cur->_right;}}}// 右为空else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{// 判读cur是parent的位置if (cur == parent->_left){parent->_left = cur->_left;}else if (cur == parent->_right){parent->_right = cur->_left;}}}// 左右都不为空else{// 先找到cur的左子树的最大值 或 右子树的最小值// parent必须初始化为cur -- 以防删除的就是头节点Node* parent = cur;Node* LeftMax = cur->_left;while (LeftMax->_right){parent = LeftMax;LeftMax = LeftMax->_right;}// 交换cur 和 LeftMax的值std::swap(cur->_key, LeftMax->_key);// 改变链接关系if (parent->_left == LeftMax){parent->_left = LeftMax->_left;}else if (parent->_right == LeftMax){parent->_right = LeftMax->_left;}cur = LeftMax;}// 集中释放 curdelete cur;return true;}}return false;
}
递归版本
- findr
无需链接关系— —不用引用即可- 递归退出条件
root == nullptr, 那就返回nullptr - 根据二叉搜索数的特性: 大了往右边走, 小了往左边走, 相等就返回当前节点的指针;
- 递归退出条件
Node* findr(const T& key)
{return _findr(_root, key);
}private:
Node*_findr(Node* root, const T& key)
{if (root == nullptr)return nullptr;if (key < root->_key){_findr(root->_left, key);}else if (key > root->_key){_findr(root->_right, key);}else{return root;}
}
- insertr
需要重新链接 -- -- 引用的妙用
总体思想 :遇到空就插入- 递归返回条件 :
遇到空, 插入后, 返回true - 二叉树的特性: 大了往右边走, 小了往左边走, 相等返回false
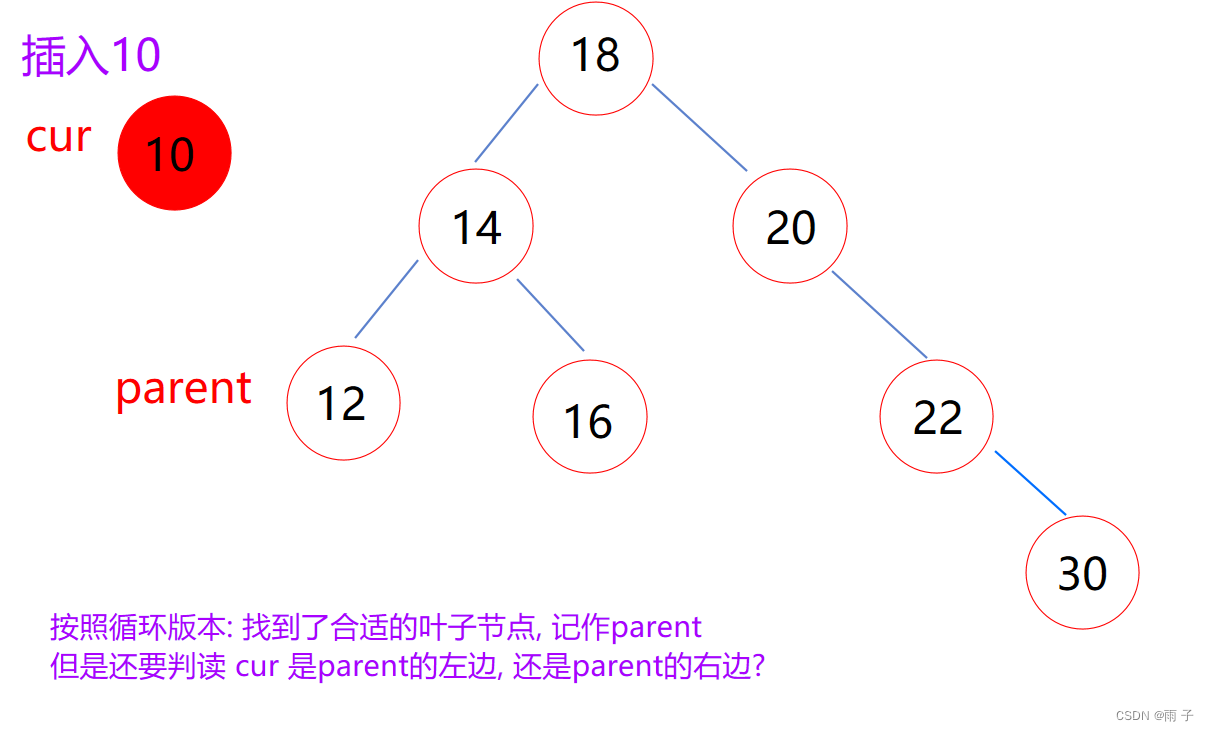
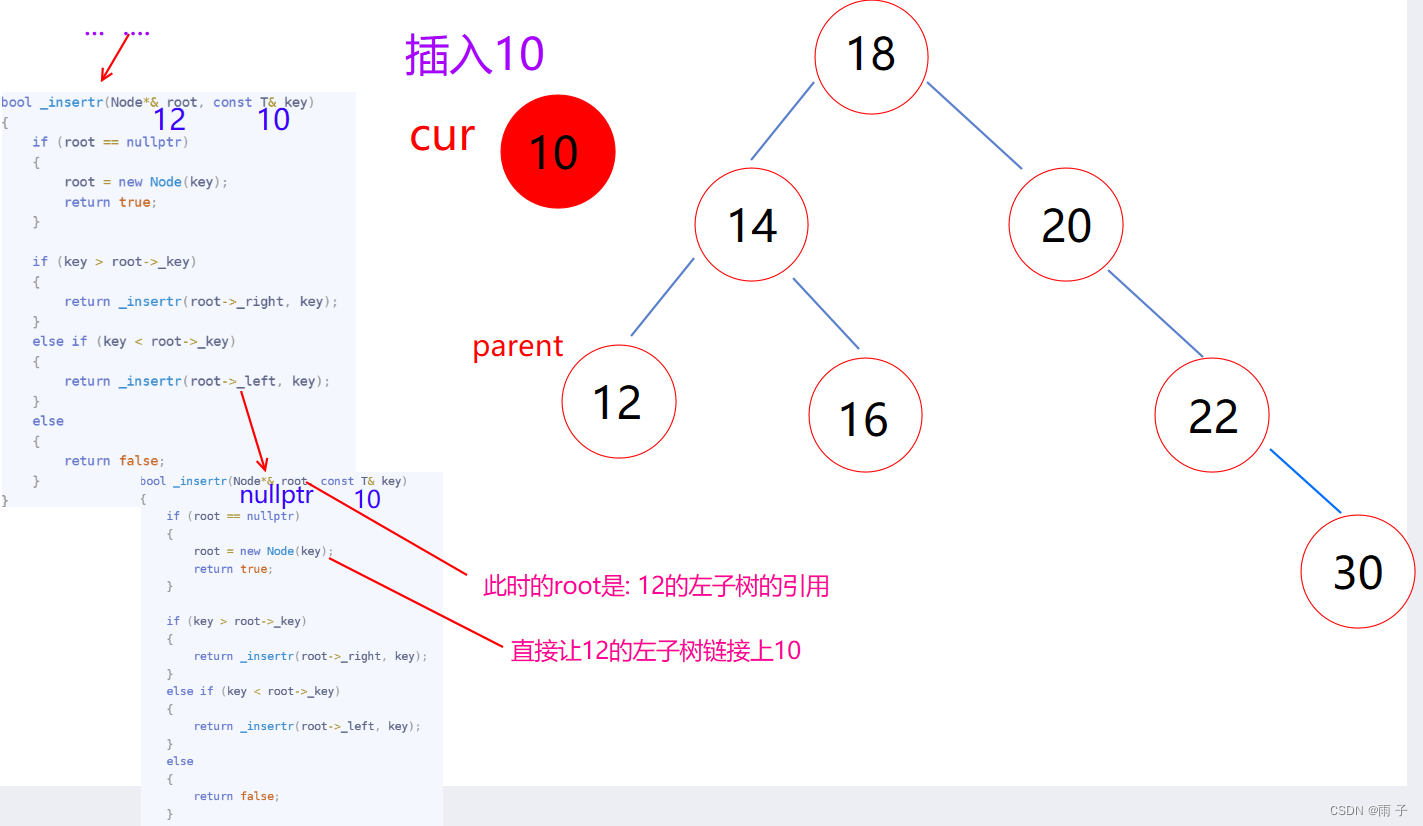
- 递归返回条件 :
bool insertr(const T& key)
{return _insertr(_root, key);
}private:
bool _insertr(Node*& root, const T& key)
{if (root == nullptr){root = new Node(key);return true;}if (key > root->_key){return _insertr(root->_right, key);}else if (key < root->_key){return _insertr(root->_left, key);}else{return false;}
}
- eraser
需要重新链接 -- -- 引用的妙用- 递归结束条件: 遇到空就返回 false
- 先找到位置, 记作 cur
- cur有三种情况 :
cur的左子树为空, cur的右子树为空, cur的左右子树都不为空; 三种情况分类讨论
这个和上面的 引用的妙用是一样的道理, 那么我就不在这里画 递归展开图
bool eraser(const T& key)
{return _eraser(_root, key);
}private:
bool _eraser(Node*& root, const T& key)
{if (root == nullptr){return false;}if (key > root->_key){_eraser(root->_right, key);}else if (key < root->_key){_eraser(root->_left, key);}else{// 由于是上面节点的引用 && 要删掉root节点// ⇒ 找一个背锅侠来代替root节点去删除Node* tem = root;// 左子树为空if (root->_left == nullptr){root = root->_right;}//右子树为空else if (root->_right == nullptr){root = root->_left;}// 左右子树都不为空else{// 找到左树的最大节点Node* maxleft = root->_left;while (maxleft->_right){maxleft = maxleft->_right;}// 交换root 和 maxleft的值std::swap(maxleft->_key, root->_key);// 重新链接root = maxleft->_left;// 背锅侠就位tem = maxleft;}// 统一删除delete tem;return true;}return false;
}
二叉搜索树的应用
二叉搜索树主要有两个版本 K版本 和 KV版本
KV版本 相较于 K版本 就多了个 value
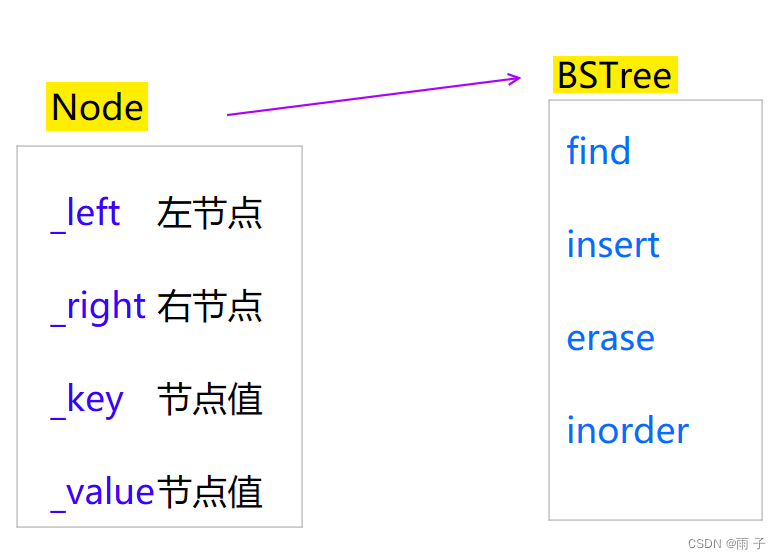
template<class K, class V>struct BSTreeNode{public:BSTreeNode(const K& key, const V& value):_left(nullptr),_right(nullptr),_key(key),_value(value){}public:BSTreeNode<K,V>* _left;BSTreeNode<K,V>* _right;K _key;V _value;};
template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:BSTree():_root(nullptr){}
private:Node* _root;
}
由于 还是对 K 进行操作 ⇒ 我们这里就不写 KV的代码了. 后面源码会附上 KV的完整代码
二叉搜索树主要应用于两种模型: K模型 和 KV模型
- K模型 — — 根据关键码Key去解决
在不在的问题
比如 : 判断单词是否拼写错误 (将词库导入二叉搜索树, 然后判断在不在)
void test1()
{// 模拟导入词库muyu::BSTree<string, string> World;World.insert("insert", "插入");World.insert("input", "输入");World.insert("output", "输出");World.insert("love", "爱情");string str;while (cin >> str){// 查找是否在词库中出现auto ret = World.find(str);if (ret){cout << "输入正确" << endl;}else{cout << "查无单词, 请重新输入" << endl;}}
}int main()
{test1();return 0;
}
运行结果:

- KV模型 — — 每一个关键码Key, 都有一个与之对应的 Value, 存在
<Key, Value>键值对
比如: 统计水果出现的次数
void test2()
{muyu::BSTree<string, int> cnt;string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜","苹果", "香蕉", "苹果", "香蕉" };for (const auto& e : arr){auto res = cnt.find(e);// 第一次插入, 次数就给个1if (!res){cnt.insert(e, 1);}// 不是第一次插入, 就在key对应的value进行++else{res->_value++;}}cnt.Inorder();
}int main()
{test2();return 0;
}
运行结果:
苹果 6
西瓜 3
香蕉 2
源码(kv)
#pragma oncenamespace muyu
{template<class K, class V>struct BSTreeNode{public:BSTreeNode(const K& key = K(), const V& value = V()):_left(nullptr),_right(nullptr),_key(key),_value(value){}public:BSTreeNode<K,V>* _left;BSTreeNode<K,V>* _right;K _key;V _value;};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:BSTree():_root(nullptr){}~BSTree(){_BSTree(_root);}bool insert(const K& key, const V& value){Node* newnode = new Node(key, value);if (_root == nullptr){_root = newnode;return true;}Node* parent = nullptr;Node* cur = _root;// 寻找插入的位置while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else{break;}}// 链接if (key > parent->_key){parent->_right = newnode;}else if (key < parent->_key){parent->_left = newnode;}else{return false;}return true;}bool insertr(const K& key){return _insertr(_root, key);}void Inorder(){_Inorder(_root);}Node* find(const K& key){return _find(_root, key);}Node* findr(const K& key){return _findr(_root, key);}bool erase(const K& key){return _erase(_root, key);}bool eraser(const K& key){return _eraser(_root, key);}private:void _BSTree(Node* root){if (root == nullptr)return;// 后序遍历进行删除_BSTree(root->_left);_BSTree(root->_right);delete root;}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);std::cout << root->_key << " " << root->_value << std::endl;_Inorder(root->_right);}Node* _insertr(Node*& root, const K& key, const V& value){if (root == nullptr){root = new Node(key, value);return root;}if (key > root->_key){return _insertr(root->_right, key);}else if (key < root->_key){return _insertr(root->_left, key);}else{return nullptr;}}Node* _find(Node* root, const K& key){Node* cur = root;while (cur){if (key > cur->_key){cur = cur->_right;}else if (key < cur->_key){cur = cur->_left;}else{return cur;}}return nullptr;}Node* _findr(Node* root, const K& key){if (root == nullptr)return nullptr;if (key < root->_key){_findr(root->_left, key);}else if (key > root->_key){_findr(root->_right, key);}else{return root;}}bool _erase(Node* root, const K& key){// 先找到位置Node* parent = root;Node* cur = root;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;} else if (key < cur->_key){parent = cur;cur = cur->_left;}// 找到了else{// 左为空if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{// 判读cur是parent的位置if (cur == parent->_left){parent->_left = cur->_right;}else if (cur == parent->_right){parent->_right = cur->_right;}}}// 右为空else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{// 判读cur是parent的位置if (cur == parent->_left){parent->_left = cur->_left;}else if (cur == parent->_right){parent->_right = cur->_left;}}}// 左右都不为空else{// 先找到cur的左子树的最大值 或 右子树的最小值Node* parent = cur;Node* LeftMax = cur->_left;while (LeftMax->_right){parent = LeftMax;LeftMax = LeftMax->_right;}// 交换cur 和 LeftMax的值std::swap(cur->_key, LeftMax->_key);// 改变链接关系if (parent->_left == LeftMax){parent->_left = LeftMax->_left;}else if (parent->_right == LeftMax){parent->_right = LeftMax->_left;}cur = LeftMax;}delete cur;return true;}}return false;}bool _eraser(Node*& root, const K& key){if (root == nullptr){return false;}if (key > root->_key){_eraser(root->_right, key);}else if (key < root->_key){_eraser(root->_left, key);}else{Node* tem = root;if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{Node* maxleft = root->_left;while (maxleft->_right){maxleft = maxleft->_right;}std::swap(maxleft->_key, root->_key);root = maxleft->_left;tem = maxleft;}delete tem;return true;}return false;}Node* _root;};
}
晚日寒鸦一片愁。柳塘新绿却温柔。若教眼底无离恨,不信人间有白头。
肠已断,泪难收。相思重上小红楼。情知已被山遮断,频倚阑干不自由。
— — 辛弃疾· 《鹧鸪天》
相关文章:

[C++随想录] 二叉搜索树
搜素二叉树 二叉搜索树的使用二叉搜索树的模拟实现(K)整体结构循环版本递归版本 二叉搜索树的应用源码(kv) 二叉搜索树的使用 二叉搜索树 相较于 普通的二叉树来说: 根节点的左子树的所有键值都 小于 根节点, 根节点的右子树的所有键值 大于 根节点根节点的 左右子树 都是 二…...
Windows Server 2019 搭建FTP站点
目录 1.添加IIS及FTP服务角色 2.创建FTP账户(用户名和密码)和组 3.设置共享文件夹的权限 4.添加及设置FTP站点 5.配置FTP防火墙支持 6.配置安全组策略 7.客户端测试 踩过的坑说明: 1.添加IIS及FTP服务角色 a.选择【开始】→【服务器…...
Ubuntu 22.04 中安装 fcitx5
Ubuntu 22.04 中安装 fcitx5 可以按照以下步骤进行: 添加 fcitx5 的 PPA 首先,添加 fcitx5 的官方 PPA: sudo add-apt-repository ppa:fcitx-team/fcitx5更新软件包列表 sudo apt update安装 fcitx5 sudo apt install fcitx5 fcitx5-conf…...
CleanMyMac X免费macOS清理系统管家
近些年伴随着苹果生态的蓬勃发展,越来越多的用户开始尝试接触Mac电脑。然而很多人上手Mac后会发现,它的使用逻辑与Windows存在很多不同,而且随着使用时间的增加,一些奇奇怪怪的文件也会占据有限的磁盘空间,进而影响使用…...

CVer从0入门NLP(一)———词向量与RNN模型
🍊作者简介:秃头小苏,致力于用最通俗的语言描述问题 🍊专栏推荐:深度学习网络原理与实战 🍊近期目标:写好专栏的每一篇文章 🍊支持小苏:点赞👍🏼、…...
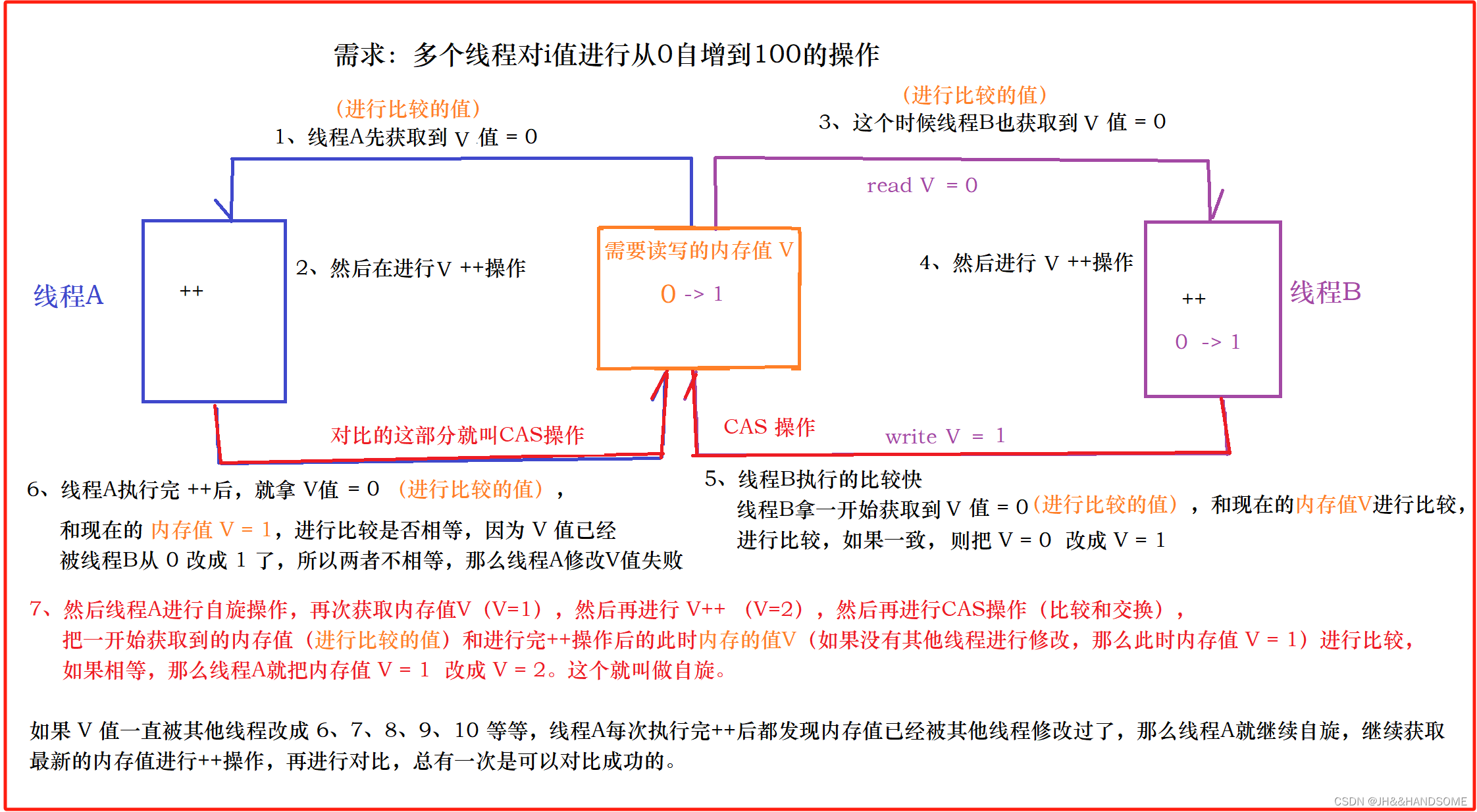
乐观锁和悲观锁
目录 悲观锁:乐观锁:CAS算法:版本号机制:write_condition 机制:时间戳:ReentrantLock 类: 独占锁:synchronized 关键字: 悲观锁: 1、理解:总是假设最坏的情况…...

用 pytorch 训练端对端验证码识别神经网络并进行 C++ 移植
文章目录 前言安装安装 pytorch安装 libtorch安装 opencv(C) 准备数据集获取训练数据下载标定 编码预分析 数据集封装格式 神经网络搭建神经网络训练神经网络测试神经网络预测C 移植模型转换通过跟踪转换为 Torch Script通过注解转换为 Torch Script 编写…...

leetcode 739. 每日温度、496. 下一个更大元素 I
739. 每日温度 给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。 示例 1: …...

Photon——Fusion服务器(Failed to find entry-points:System.Exception: )
文章目录 前言解决方案:1.报警信息如下2.选择3d urp3.引入Fusion之后选择包管理,点击Burst中的Advanced Project Settings4.勾选两个预设选项5.引入官网unity.burst6.更新后报警消失总结前言 制作局域网游戏,出现未找到进入点报警 Failed to find entry-points 解决方案: …...

双十一必买好物,这四款好物你值得拥有
随着科技的不断发展,智能家电已经成为我们生活中不可或缺的一部分。在双十一期间,各大品牌都会推出各种优惠活动,以更优惠的价格购买到心仪的智能家电。比如智能超声波清洗机,智能门锁,它们不仅提高了我们的生活质量&a…...

视频号视频如何下载(WeChatVideoDownloader)
背景介绍 最近需要一个视频号里面的视频进行宣传用,网上找了很多方法都不行,特别是下载抓包工具Fiddler,然后监控HTTPS请求的,截取URL把URL中20302改成20304,再用IDM工具下载对应的资源,最后修改后缀名.mp…...

【Java-框架-SpringMVC】(01) SpringMVC框架的简单创建与使用,快速上手 - 简易版
前言 【描述】 "SpringMVC"框架的简单创建与使用,快速上手; 【环境】 系统"Windows",软件"IntelliJ IDEA 2021.1.3(Ultimate Edition)";“Java版本"1.8.0_202”,“Spring"版…...
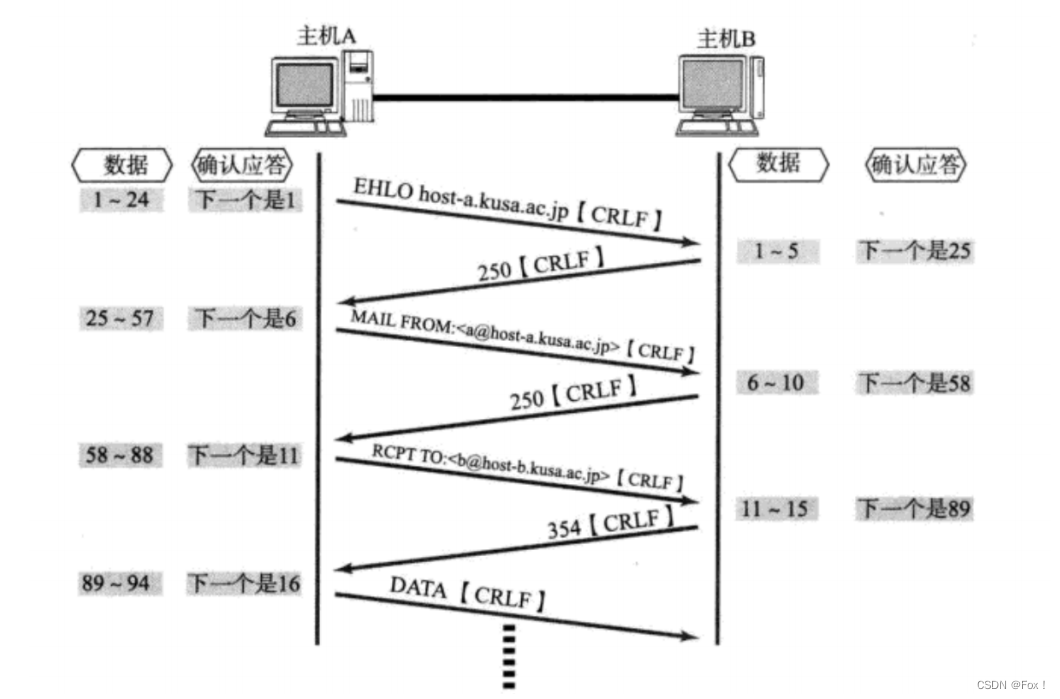
【计算机网络】UDP/TCP协议
文章目录 :peach:1 UDP协议:peach:1.1 :apple:UDP协议端格式:apple:1.2 :apple:UDP的特点:apple:1.3 :apple:UDP的缓冲区:apple:1.4 :apple:UDP使用注意事项:apple:1.5 :apple:基于UDP的应用层协议:apple: 2 :peach:TCP协议:peach:2.1 :apple:TCP协议端格式:apple:2.2 :apple:确…...

【前端设计模式】之享元模式
享元模式是一种结构型设计模式,它通过共享对象来减少内存使用和提高性能。在前端开发中,享元模式可以用于优化大量相似对象的创建和管理,从而提高页面的加载速度和用户体验。 享元模式特性 共享对象:享元模式通过共享相似对象来…...

C++前缀和算法:合并石头的最低成本原理、源码及测试用例
本文涉及的基础知识点 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 动态规划,日后完成。 题目 有 n 堆石头排成一排,第 i 堆中有 stones[i] 块石头。 每次 移动 需要将 连续的 k 堆石头合并为一堆,而…...

maven 安装本地jar失败 错误指南
Maven 安装本地 jar 失败 安装命令: mvn install:install-file -Dfile文件路径地址 -DgroupIdcom.allinpay.sdk -DartifactIdtop-sdk-java -Dversion1.0.5 -Dpackagingjar 错误描述 : Unknown lifecycle phase “.allinpay.sdk”. You must specify a valid lifecycle phase o…...
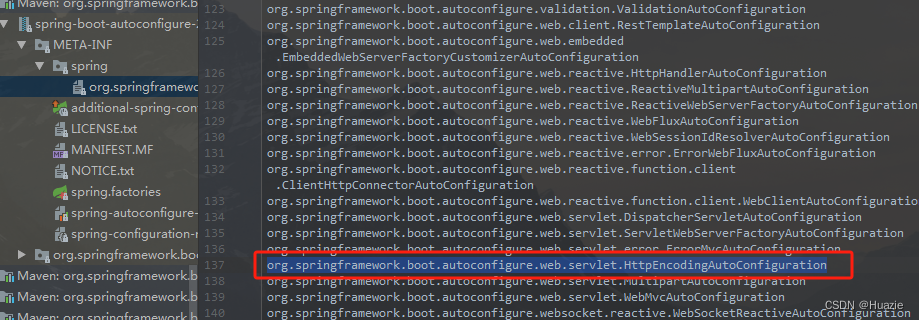
【Spring Boot 源码学习】HttpEncodingAutoConfiguration 详解
Spring Boot 源码学习系列 HttpEncodingAutoConfiguration 详解 引言往期内容主要内容1. CharacterEncodingFilter2. HttpEncodingAutoConfiguration2.1 加载自动配置组件2.2 过滤自动配置组件2.2.1 涉及注解2.2.2 characterEncodingFilter 方法2.2.3 localeCharsetMappingsCus…...
uni-app--》基于小程序开发的电商平台项目实战(七)完结篇
🏍️作者简介:大家好,我是亦世凡华、渴望知识储备自己的一名在校大学生 🛵个人主页:亦世凡华、 🛺系列专栏:uni-app 🚲座右铭:人生亦可燃烧,亦可腐败…...

手写banner切换方式
<template><!-- banner轮播切换 --><div class"banner-wrapper"><div class"banner-info"><ul class"box" ref"box"><li v-for"(item, index) in bannerList" :key"index">&…...
技术文档工具『Writerside』抢鲜体验
前言 2023 年 10 月 16 日,JetBrains 宣布以早期访问状态推出 Writerside,基于 IntelliJ 平台的 JetBrains IDE,开发人员可使用它编写、构建、测试和发布技术文档,可以作为 JetBrains IDE 中的插件使用,也可以作为独立…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
