当前位置： 首页 > news >正文

2023年9月青少年软件编程（C 语言） 等级考试试卷（七级）

news 2026/2/10 17:14:04

青少年软件编程（C/C++）7级等级考试真题试卷（2023年9月）
编程题
第 1 题    红与黑（2023.9）

有一间长方形的房子，地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上，只能向相邻的黑色瓷砖移动。请写一个程序，计算你总共能够到达多少块黑色的瓷砖。

输入

包括多个数据集合。每个数据集合的第一行是两个整数W和H，分别表示x方向和y方向瓷砖的数量。W和H都不超过20。在接下来的H行中，每行包括W个字符。每个字符表示一块瓷砖的颜色，规则如下 1）‘.’：黑色的瓷砖； 2）‘#’：白色的瓷砖； 3）‘@’：黑色的瓷砖，并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。 当在一行中读入的是两个零时，表示输入结束。

输出

对每个数据集合，分别输出一行，显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。

样例输入

6 9 
....#. 
.....# 
...... 
...... 
...... 
...... 
...... 
#@...# 
.#..#. 
0 0
样例输出

45



第 2 题   重建二叉树

给定一棵二叉树的前序遍历和中序遍历的结果，求其后序遍历。

输入

输入可能有多组，以EOF结束。 每组输入包含两个字符串，分别为树的前序遍历和中序遍历。每个字符串中只包含大写字母且互不重复。

输出

对于每组输入，用一行来输出它后序遍历结果。

样例输入

DBACEGF ABCDEFG
BCAD CBAD
样例输出

ACBFGED
CDAB

答案和更多内容请查看网站：【试卷中心 -- C/C++ 五级/六级/其它】

网站链接 

青少年软件编程历年真题模拟题实时更新

相关文章：

2023年9月青少年软件编程（C 语言） 等级考试试卷（七级）

青少年软件编程（C/C）7级等级考试真题试卷（2023年9月） 编程题第 1 题 红与黑（2023.9） 有一间长方形的房子，地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上&#xff0c…...

编程日记 2023/10/23 12:35:52

鸿鹄工程项目管理系统 Spring Cloud+Spring Boot+Mybatis+Vue+ElementUI+前后端分离构建工程项目管理系统项目背景

鸿鹄工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离构建工程项目管理系统 1. 项目背景 一、随着公司的快速发展，企业人员和经营规模不断壮大。为了提高工程管理效率、减轻劳动强度、提高信息处理速度和准确性，公司对内部工程管…...

编程日记 2023/10/23 12:34:50

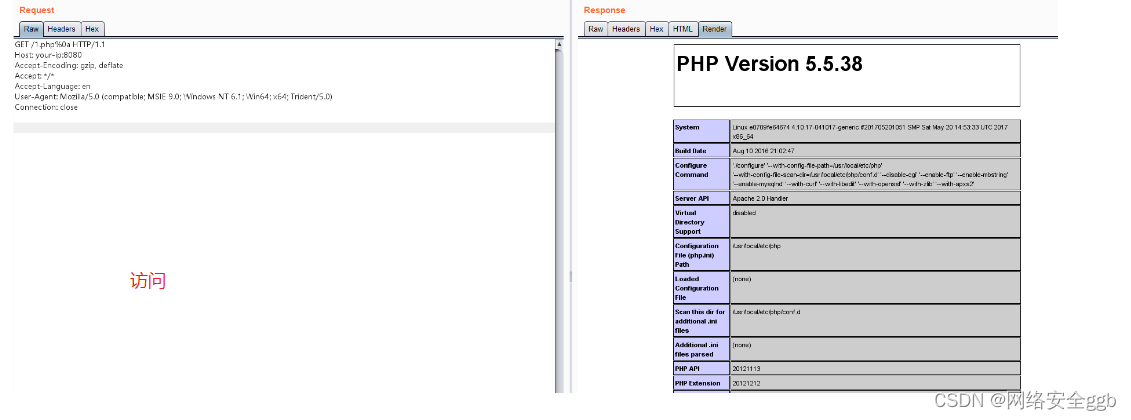
apache httpd 换行解析漏洞

原理 Apache HTTPD是一款HTTP服务器，它可以通过mod_php来运行PHP网页。其2.4.0~2.4.29版本中存在一个解析漏洞，在解析PHP时，1.php\x0A将被按照PHP后缀进行解析，导致绕过一些服务器的安全策略。 漏洞编号 cve-2017-15715 环境…...

编程日记 2023/10/23 12:33:49

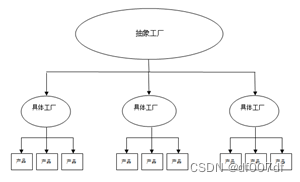
【设计模式】工厂模式

工厂模式 1.什么是工厂模式 它提供了一种创建对象的最佳方式。在工厂模式中，我们在创建对象时不会对客户端暴露创建逻辑，并且是通过使用一个共同的接口来指向新创建的对象。实现了创建者和调用者分离，工厂模式分为简单工厂、工厂方法、抽象…...

编程日记 2023/10/23 12:32:48

C++二分算法的应用：寻找峰值原理、源码及测试用例

说明 此文是课程https://edu.csdn.net/course/detail/38771 的讲义。 源码下载：https://download.csdn.net/download/he_zhidan/88458478 题目 长度为n的数组nums，请返回任意一峰值的索引。符合以下条件之一i便是峰值的索引。 n等于1 i等于0 n>…...

编程日记 2023/10/23 12:31:47

外汇天眼：本周无牌裸奔平台名单出炉，你踩“坑”了么？！！

监管信息早知道！外汇天眼将每周定期公布监管牌照状态发生变化的交易商，以供投资者参考，规避投资风险。如果平台天眼评分过高，建议投资者谨慎选择，因为在外汇天眼评分高不代表平台没问题！ 以下是监管牌照发生…...

编程日记 2023/10/23 12:29:45

10 读写锁ReentrantReadWriteLock

1 介绍 为什么要使用读写锁？ 需要高并发读取和较低并发写入的应用程序，降低锁的粒度，提高系统性能 使用场景： 读多写少的共享资源 缓存管理：读 >> 写，控制多个线程同时读缓存，需要刷新o…...

编程日记 2023/10/23 12:28:44

laravel队列

laravel redis队列 1、创建job队列任务 php artisan make:job StoreUser执行上述命令后&#xff0c;会生成app/Jobs/StoreUser.php文件&#xff0c;编辑文件内容如下&#xff1a; <?phpnamespace App\Jobs;use Illuminate\Bus\Queueable; use Illuminate\Contracts\Queu…...

编程日记 2023/10/23 12:27:43

【计算机网络】TCP 协议的相关特性

TCP&#xff08;传输控制协议&#xff09;是一种面向连接的、可靠的、基于字节流的协议。以下是TCP协议的相关特性&#xff1a; 可靠性&#xff1a;TCP通过确认和重传机制保证数据的可靠传输。 面向连接&#xff1a;TCP在传输数据前需要先建立连接。连接的建立过程包括三次握手…...

编程日记 2023/10/23 12:26:42

[软件安装] tmux安装及相关事项

tmux安装及相关事项 tmux是一个终端复用工具&#xff0c;可以在单个终端窗口中同时运行多个终端会话。安装tmux可以提高工作效率&#xff0c;使命令行操作更加方便。 1. 安装tmux&#xff1a; 在Linux系统下&#xff0c;可以使用包管理器来安装tmux&#xff0c;比如在Ubuntu…...

编程日记 2023/10/23 12:25:39

leetcode 887 ——扔鸡蛋

题目大意&#xff1a; 你有k个鸡蛋&#xff0c;对n层楼的建筑&#xff0c;请确认在f层扔鸡蛋鸡蛋恰好不会破碎的最少次数&#xff08;f满足 0 < f < n&#xff09;。 方法一&#xff1a; 状态&#xff1a;即会发生变化的量&#xff0c;很明显有两个&#xff0c;当前拥有…...

编程日记 2023/10/23 12:21:30

自动化运维ansible(role)

一、role的介绍 1、Roles称为角色&#xff0c;本质上是为简化playbook配置文件而产生的一种特殊的方法。 2、简单来说&#xff0c;roles就是将原本在一个yaml中的文件进行规则化分散&#xff0c;封装到不同的目录下&#xff0c;从而简化playbook的yaml配置文件大小。从其实现方…...

编程日记 2023/10/23 12:20:29

linux命令笔记

创建文件夹 sudo mkdir 文件夹名vim笔记 vim的查找和退出查找 进入vim 按/ 输入内容即可查找 按enter结束查找vim创建文件并在里面写东西 比如创建文件为 hello.cpp vim hello.cpp查看所有文件 # 查看所有文件&#xff0c;并以列表的形式查看&#xff0c;显示出文件大小 …...

编程日记 2023/10/23 12:19:28

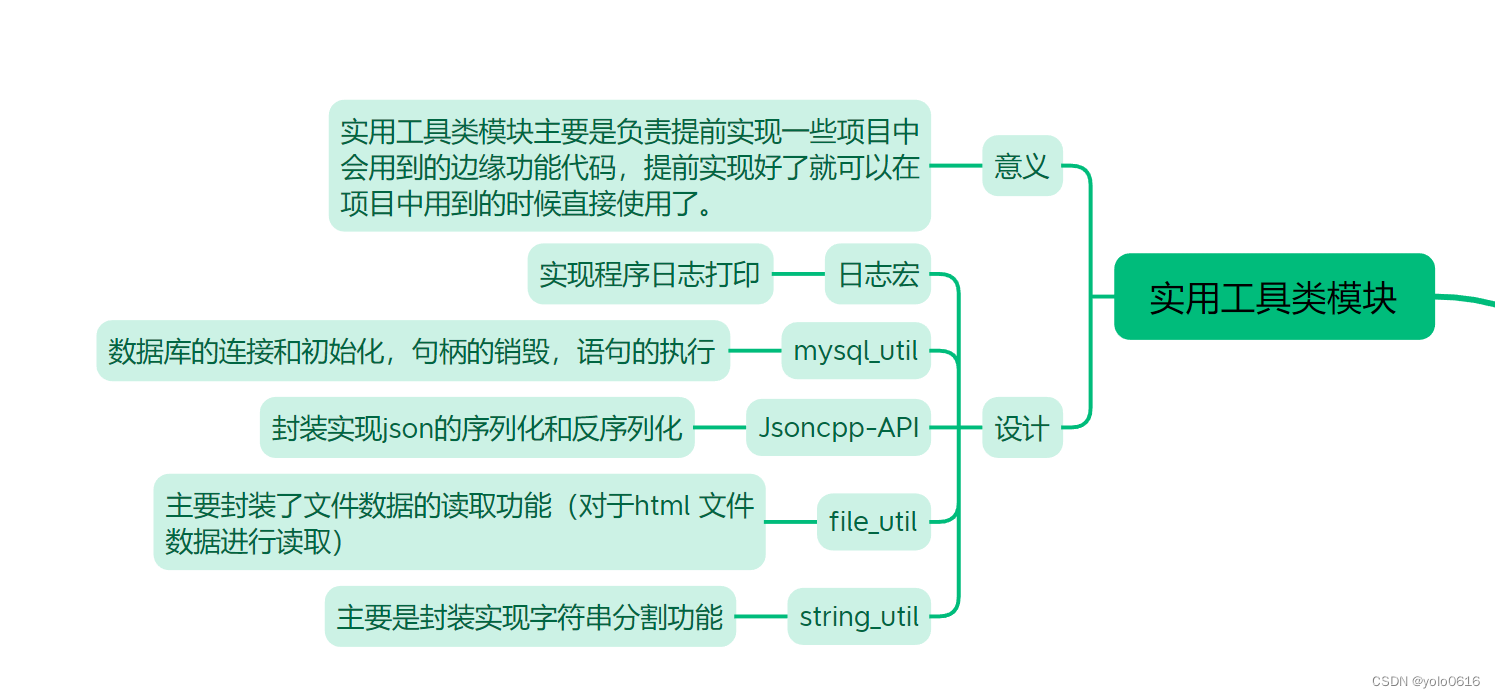
2.3.C++项目：网络版五子棋对战之实用工具类模块的设计

文章目录 一、实用工具类模块&#xff08;一&#xff09;功能 二、设计和封装&#xff08;一&#xff09;日志宏封装&#xff08;二&#xff09;mysql_util封装&#xff08;三&#xff09;Jsoncpp-API封装&#xff08;四&#xff09;file_util封装&#xff08;五&#xff09;st…...

编程日记 2023/10/23 12:17:25

跳跃游戏----题解报告

题目&#xff1a;力扣&#xff08;LeetCode&#xff09;官网 - 全球极客挚爱的技术成长平台 题解&#xff1a; 其实就直接挨着跳就行了&#xff0c;循环中不断更新k&#xff0c;不停比较k和当前位置跳跃的最大值即可 代码&#xff1a; public boolean canJump(int[] nums) …...

编程日记 2023/10/23 12:16:23

SpringBoot下的代理注解

EnableAspectJAutoProxy Target(ElementType.TYPE) Retention(RetentionPolicy.RUNTIME) Documented Import(AspectJAutoProxyRegistrar.class) public interface EnableAspectJAutoProxy {// 是否代理目标对象&#xff0c;ture:使用CGLIB代理 fasle:使用JDK代理boolean proxy…...

编程日记 2023/10/23 12:15:22

[C++随想录] 二叉搜索树

搜素二叉树 二叉搜索树的使用二叉搜索树的模拟实现(K)整体结构循环版本递归版本 二叉搜索树的应用源码(kv) 二叉搜索树的使用 二叉搜索树 相较于 普通的二叉树来说: 根节点的左子树的所有键值都 小于 根节点, 根节点的右子树的所有键值 大于 根节点根节点的 左右子树 都是 二…...

编程日记 2023/10/23 12:14:20

Windows Server 2019 搭建FTP站点

目录 1.添加IIS及FTP服务角色 2.创建FTP账户&#xff08;用户名和密码&#xff09;和组 3.设置共享文件夹的权限 4.添加及设置FTP站点 5.配置FTP防火墙支持 6.配置安全组策略 7.客户端测试 踩过的坑说明&#xff1a; 1.添加IIS及FTP服务角色 a.选择【开始】→【服务器…...

编程日记 2023/10/23 12:13:18

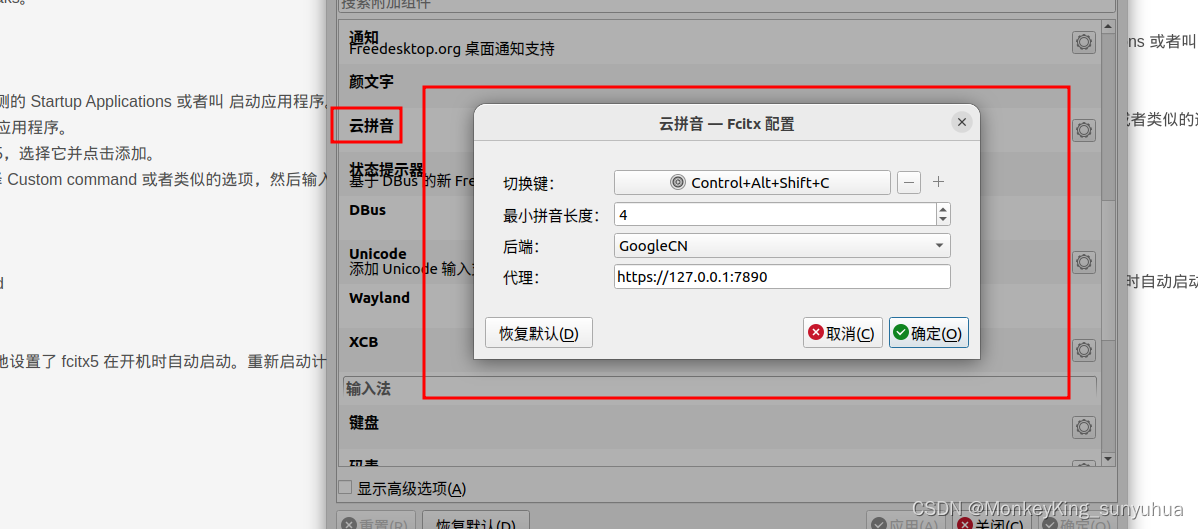
Ubuntu 22.04 中安装 fcitx5

Ubuntu 22.04 中安装 fcitx5 可以按照以下步骤进行&#xff1a; 添加 fcitx5 的 PPA 首先&#xff0c;添加 fcitx5 的官方 PPA&#xff1a; sudo add-apt-repository ppa:fcitx-team/fcitx5更新软件包列表 sudo apt update安装 fcitx5 sudo apt install fcitx5 fcitx5-conf…...

编程日记 2023/10/23 12:12:17

CleanMyMac X免费macOS清理系统管家

近些年伴随着苹果生态的蓬勃发展&#xff0c;越来越多的用户开始尝试接触Mac电脑。然而很多人上手Mac后会发现&#xff0c;它的使用逻辑与Windows存在很多不同&#xff0c;而且随着使用时间的增加&#xff0c;一些奇奇怪怪的文件也会占据有限的磁盘空间&#xff0c;进而影响使用…...

编程日记 2023/10/23 12:11:14

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析

一、变量声明设计&#xff1a;let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性&#xff0c;这种设计体现了语言的核心哲学。以下是深度解析&#xff1a; 1.1 设计理念剖析 安全优先原则&#xff1a;默认不可变强制开发者明确声明意图 let x 5; …...

编程新知 2025/9/28 20:12:12

论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（二）

HoST框架核心实现方法详解 - 论文深度解读（第二部分） 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章： 论文深度解读 + 算法与代码分析（二） 作者机构： 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题： 人形机器人…...

编程新知 2026/2/9 0:12:12

HTML 列表、表格、表单

1 列表标签 作用&#xff1a;布局内容排列整齐的区域 列表分类&#xff1a;无序列表、有序列表、定义列表。 例如&#xff1a; 1.1 无序列表 标签&#xff1a;ul 嵌套 li&#xff0c;ul是无序列表&#xff0c;li是列表条目。 注意事项&#xff1a; ul 标签里面只能包裹 li…...

编程新知 2026/1/24 22:33:33

Spring AI 入门：Java 开发者的生成式 AI 实践之路

一、Spring AI 简介 在人工智能技术快速迭代的今天&#xff0c;Spring AI 作为 Spring 生态系统的新生力量&#xff0c;正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务&#xff08;如 OpenAI、Anthropic&#xff09;的无缝对接&…...

编程新知 2025/12/25 18:03:56

今日科技热点速览

&#x1f525; 今日科技热点速览 &#x1f3ae; 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售&#xff0c;主打更强图形性能与沉浸式体验&#xff0c;支持多模态交互&#xff0c;受到全球玩家热捧 。 &#x1f916; 人工智能持续突破 DeepSeek-R1&…...

编程新知 2025/11/20 14:26:29

Rapidio门铃消息FIFO溢出机制

关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系&#xff0c;以下是深入解析&#xff1a; 门铃FIFO溢出的本质 在RapidIO系统中&#xff0c;门铃消息FIFO是硬件控制器内部的缓冲区&#xff0c;用于临时存储接收到的门铃消息&#xff08;Doorbell Message&#xff09;。…...

编程新知 2026/1/7 1:29:19

dify打造数据可视化图表

一、概述 在日常工作和学习中&#xff0c;我们经常需要和数据打交道。无论是分析报告、项目展示&#xff0c;还是简单的数据洞察&#xff0c;一个清晰直观的图表&#xff0c;往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server&#xff0c;由蚂蚁集团 AntV 团队…...

编程新知 2026/1/20 20:10:03

AI，如何重构理解、匹配与决策？

AI 时代&#xff0c;我们如何理解消费&#xff1f; 作者&#xff5c;王彬 封面&#xff5c;Unplash 人们通过信息理解世界。 曾几何时&#xff0c;PC 与移动互联网重塑了人们的购物路径&#xff1a;信息变得唾手可得&#xff0c;商品决策变得高度依赖内容。 但 AI 时代的来…...

编程新知 2026/1/30 2:33:11

Python 包管理器 uv 介绍

Python 包管理器 uv 全面介绍 uv 是由 Astral&#xff08;热门工具 Ruff 的开发者&#xff09;推出的下一代高性能 Python 包管理器和构建工具&#xff0c;用 Rust 编写。它旨在解决传统工具&#xff08;如 pip、virtualenv、pip-tools&#xff09;的性能瓶颈&#xff0c;同时…...

编程新知 2026/2/7 10:47:09

Redis的发布订阅模式与专业的 MQ（如 Kafka, RabbitMQ）相比，优缺点是什么？适用于哪些场景？

Redis 的发布订阅&#xff08;Pub/Sub&#xff09;模式与专业的 MQ&#xff08;Message Queue&#xff09;如 Kafka、RabbitMQ 进行比较&#xff0c;核心的权衡点在于&#xff1a;简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

编程新知 2025/12/4 2:32:37