计算组合数Cnk即从n个不同数中选出k个不同数共有多少种方法math.comb(n,k)
【小白从小学Python、C、Java】
【计算机等级考试+500强双证书】
【Python-数据分析】
计算组合数Cnk
即从n个不同数中选出k个不同数共有多少种方法
math.comb(n,k)
以下python代码输出结果是?
import math
print("【执行】print(math.comb(3,1))")
print(math.comb(3,1))
print("【执行】print(math.comb(3,2))")
print(math.comb(3,2))
print("【执行】print(math.comb(3,3))")
print(math.comb(3,3))
A选项:3 6 9
B选项:2 3 5
C选项:1 2 3
D选项:3 3 1
答案
正确答案是:D
温馨期待
期待大家提出宝贵建议,互相交流,收获更大
欢迎大家转发,一起传播知识和正能量,帮助到更多人。期待大家提出宝贵改进建议,互相交流,收获更大。辛苦大家转发时注明出处(也是咱们公益编程交流群的入口网址),刘经纬老师共享知识相关文件下载地址为:https://liujingwei.cn
图1 问题解析

图2 题目运行代码

相关文章:

计算组合数Cnk即从n个不同数中选出k个不同数共有多少种方法math.comb(n,k)
【小白从小学Python、C、Java】 【计算机等级考试500强双证书】 【Python-数据分析】 计算组合数Cnk 即从n个不同数中选出k个不同数共有多少种方法 math.comb(n,k) 以下python代码输出结果是? import math print("【执行】print(math.comb(3,1))") print(math.comb(…...

工厂设计模式
基本概念:为创建对象提供过渡接口,以便将创建对象的具体过程屏蔽隔离起来,达到提高灵活性的目的。分为三类:简单工厂模式Simple Factory:不利于产生系列产品;工厂方法模式Factory Method:又称为…...
IO多路转接 —— poll和epoll
文章目录1. poll1.1 poll的函数接口1.2 poll的简单测试程序1.3 poll的优缺点分析2. epoll2.1 epoll的函数接口2.2 epoll的工作原理2.3 epoll的工作模式(LT,ET)2.4 epoll的简易服务器实现(默认是LT工作模式)前言: 接上文讲述的select,它有缺点,…...

计算机网络整理-问答
1. 程序工作的时候网络各层的状态 如下图所示: 1. TCP 在进行三次握手的时候,IP 层和 MAC 层对应都有什么操作呢? TCP 三次握手是通过在传输层建立连接的一个过程,在这个过程中,TCP 和 IP 层、MAC 层都起到了重要的…...
JS 实现抛物线动画案例
相信大家都有浏览过,很多购物网站购物车的添加商品动画,今天,我们就手写一个简单的抛物线动画,先上案例: 一、绘制页面 我们这里简单实现,一个按钮,一个购物车图标,样式这里直接跳过…...
CSGO搬砖项目,23年最适合小白的项目!
大家好,我是阿阳 不懂的小伙伴,咱继续听我娓娓道来 steam搬砖主要涉及的是csgo游戏平台装备的一个搬运,比较很好理解,主要就是道具的搬运工,简单来讲就是,从国外steam游戏平台购买装备,再挂到…...
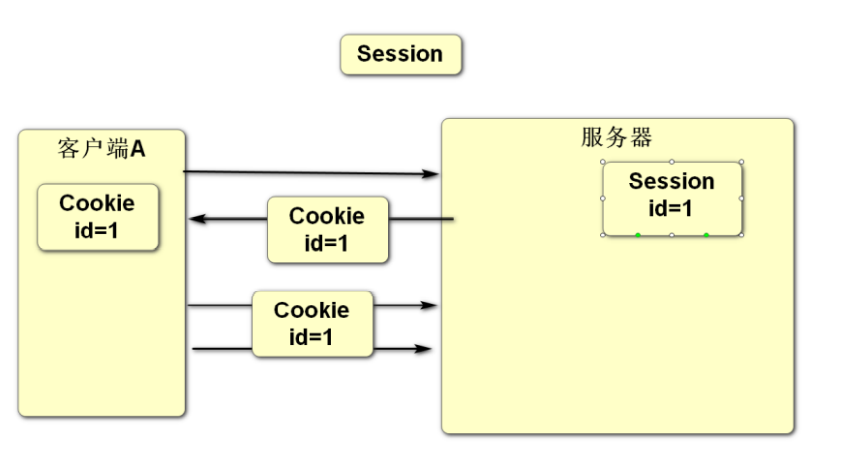
谈谈会话管理
客户端和服务器之间进行数据传输遵循的是HTTP协议, 此协议属于无状态协议(一次请求对应一次响应, 响应完之后断开连接), 服务器是无法跟踪客户端的请求, 通过cookie技术可以给客户端添加一个标识, 客户端之后发出的每次请求都会带着这个标识从而让服务器识别此客户端, 但由于co…...
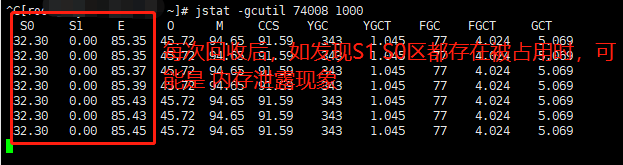
Linux查看JVM FULL GC频率
查看系统的full gc频率,可以使用jstack命令一、采用top命令定位进程登录服务器,执行top命令,查看CPU占用情况,找到进程的pid二、使用jstack命令统计垃圾回收jstat -gc pid 5000即会每5秒一次显示进程号为pid的java进程的GC情况以上…...

java世界String的那些事
String的创建机理: 由于String在Java世界中使用过于频繁,Java为了避免在一个系统中产生大量的String对象,引入了字符串常量池。其运行机制是:创建一个字符串时,首先检查池中是否有值相同的字符串对象,如果…...

【图像配准】多图配准/不同特征提取算法/匹配器比较测试
前言 本文首先完成之前专栏前置博文未完成的多图配准拼接任务,其次对不同特征提取器/匹配器效率进行进一步实验探究。 各类算法原理简述 看到有博文[1]指出,在速度方面SIFT<SURF<BRISK<FREAK<ORB,在对有较大模糊的图像配准时&…...
2023金三银四季跳槽季,啃完这软件测试面试题,跳槽不就稳稳的了
前言 2023年也到来了,接近我们所说的“金三银四”也正在执行了,时间晃眼就过去了,有的人为了2023跳槽早早做足了准备,有的人在临阵磨刀,想必屏幕前的你也想在2023年涨薪吧,那么问题来了,怎么才…...
【C++详解】——vector类
📖 前言:本期介绍vector类。 目录🕒 1. vector的介绍🕒 2. vector的使用🕘 2.1 定义🕘 2.2 iterator🕘 2.3 空间增长🕘 2.4 增删查改🕒 2. vector的模拟实现🕘…...
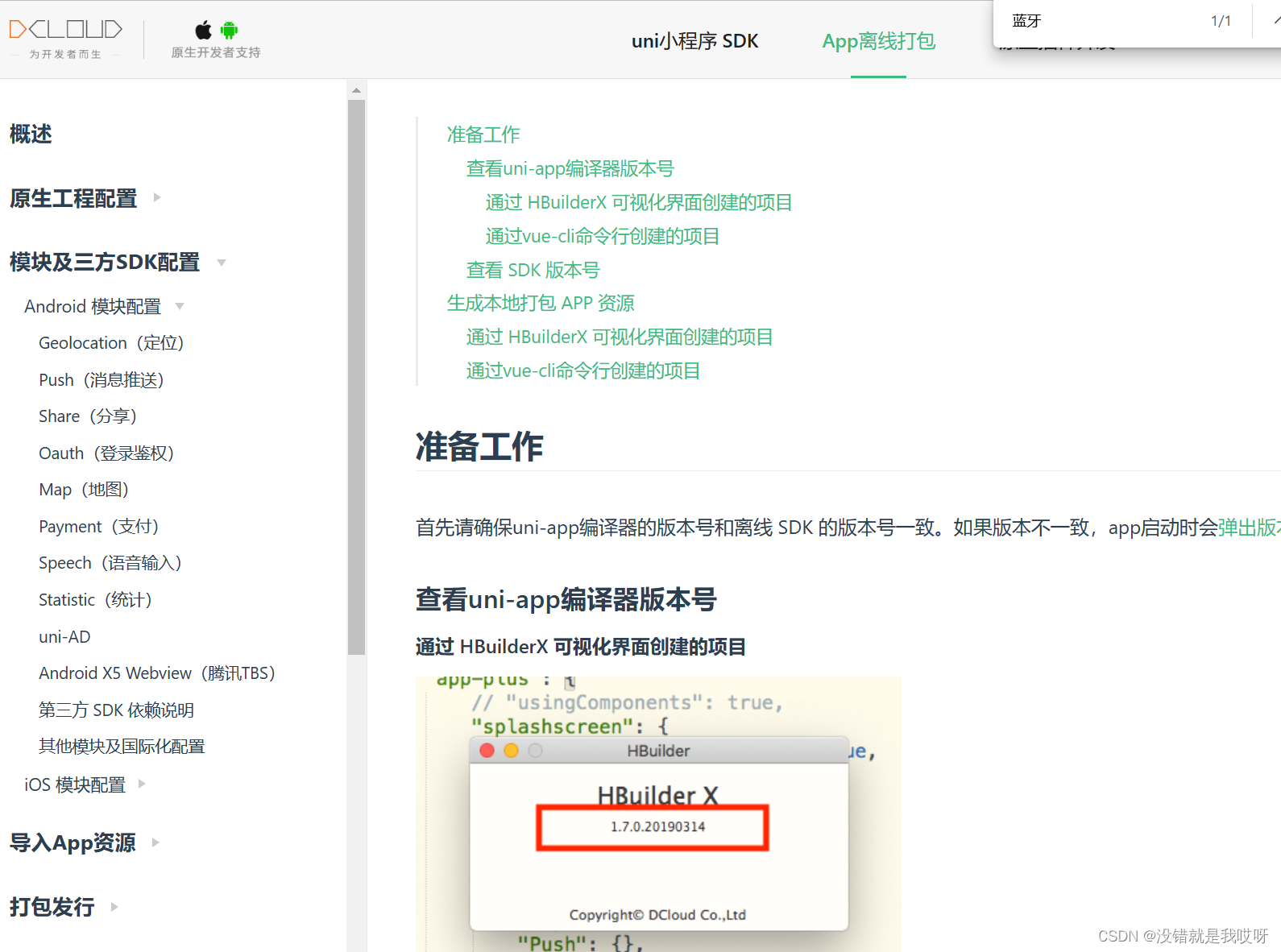
uniapp 离线本地打包
uniapp打包教程地址 https://nativesupport.dcloud.net.cn/AppDocs/usesdk/android.html点击查看 需要的环境: java (1.8)离线SDK(上面的连接下载即可)Android Studio(同上) 配置环境变量 依次点击“计算机”-“属性”&#…...
)
初识马尔科夫模型(Markov Model)
初识马尔科夫模型(Markov Model)一、概念二、性质三、学习步骤一、概念 马尔科夫模型(Markov Model)是一种概率模型,用于描述随机系统中随时间变化的概率分布。马尔科夫模型基于马尔科夫假设,即当前状态只…...
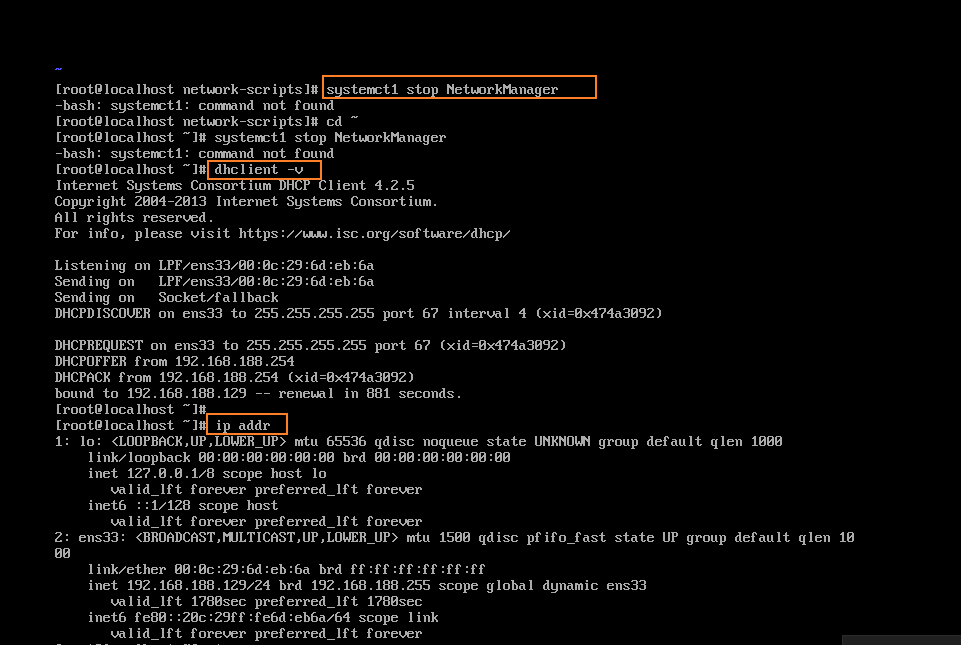
CentOS7 ifconfig(或 ip addr)命令不显示IP地址
问题(因为当时没有存图 所以这个图上是网上找的 )解决办法第一:可能是本地服务没有开启,检查本地服务。如图所示,检查这两个服务是否开启。注:如何快速找到服务 可以把光标放在其中一个上面 然后按下VM就可…...

2023/2/10总结
拓扑排序 拓扑排序是在一个有向无环图(DAG)所有顶点的线性排序。 拓扑排序核心思想非常简单,就是先找一个入度为0的顶点输出,再从图中删除该顶点和以它为起点的有向边。继续上面的操作知道所有的顶点访问完为止。 入度…...

2023最新版!宝塔面板Docker自建Bitwarden密码管理
Powered by:NEFU AB-IN 请一定要结合B站视频食用!!!!,下面的博客总体来说只是起到提纲作用 B站视频链接!!! 文章目录2023最新版!宝塔面板Docker自建Bitwarden密码管理前…...

【Hello Linux】 Linux基础命令
作者:小萌新 专栏:Linux 作者简介:大二学生 希望能和大家一起进步! 本篇博客简介:介绍Linux的基础命令 Linux基础命令ls指令lsls -als -dls -ils -sls -lls -nls -Fls -rls -tls -Rls -1总结思维导图pwd指令whoami指令…...
151、【动态规划】leetcode ——2. 01背包问题:二维数组+一维数组(C++版本)
题目描述 原题链接:2. 01背包问题 解题思路 (1)二维dp数组 动态规划五步曲: (1)dp[i][j]的含义: 容量为j时,从物品1-物品i中取物品,可达到的最大价值 (2…...

2023-02-09 - 3 Elasticsearch基础操作
本章主要介绍ES的基础操作,具体包括索引、映射和文档的相关操作。其中,在文档操作中将分别介绍单条操作和批量操作。在生产实践中经常会通过程序对文档进行操作,因此在介绍文档操作时会分别介绍DSL请求形式和Java的高级REST编码形式。 1 索引…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
EasyRTC音视频实时通话功能在WebRTC与智能硬件整合中的应用与优势
一、WebRTC与智能硬件整合趋势 随着物联网和实时通信需求的爆发式增长,WebRTC作为开源实时通信技术,为浏览器与移动应用提供免插件的音视频通信能力,在智能硬件领域的融合应用已成必然趋势。智能硬件不再局限于单一功能,对实时…...

JavaScript 标签加载
目录 JavaScript 标签加载script 标签的 async 和 defer 属性,分别代表什么,有什么区别1. 普通 script 标签2. async 属性3. defer 属性4. type"module"5. 各种加载方式的对比6. 使用建议 JavaScript 标签加载 script 标签的 async 和 defer …...
