【数据库】第二章 关系数据库
第二章 关系数据库
2.1关系数据结构及形式化定义
关系
域(domain) :域是一组具有相同数据类型的值的集合,可以取值的个数叫基数
笛卡尔积 :一个记录叫做一个元组(tuple),元组中每一个属性值,叫一个分量
基数: 域的元素个数
笛卡尔乘积是指在数学中,两个集合X和Y的笛卡尔积,表示为X×Y,所有有序对
假设集合A={a, b},集合B={0, 1, 2},则两个集合的笛卡尔积为{(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}。
基数为2 x 3=6

关系: 关系是笛卡尔积的子集,每一行对应一个元组,每一列对应一个域,列名叫做属性(attribute)
R是表的名字,n是属性个数,叫做关系的目或度(degree)
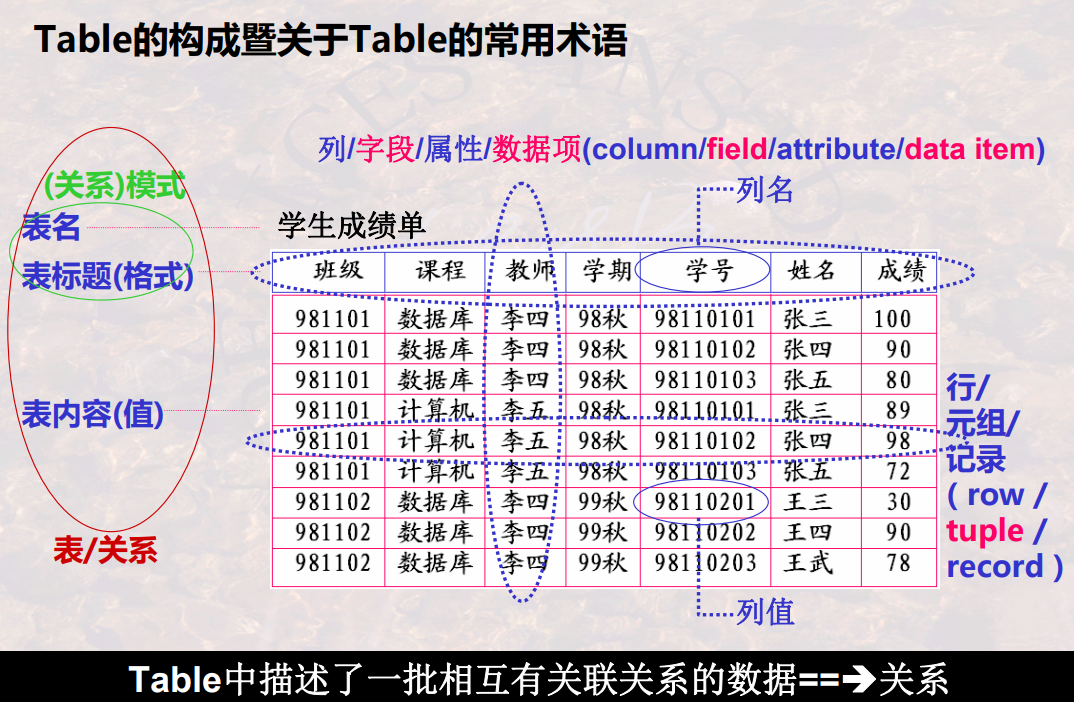
候选码(candidate key): 某一属性组的值能唯一标识一个元组,而他的子集不能,则称该属性组为候选码。
主码(primary key): 若一个关系有多个候选码,则选定其中一个为主码。
主属性: 属于候选码的属性叫主属性。其他属性叫非主属性或非码属性
全码: 若关系模式的所有属性都是这个关系模式的候选码,称为全码。
外码:依赖于另一个关系的主码
关系的三种类型
- 基本关系(基本表/基表):实际存在的表
- 查询表:查询结果对应的表
- 视图表:是由基本表或其他视图表导出的表,是虚表,不对应实际存储的数据
基本关系的6条性质:
- 列是同质的。(同一数据类型)
- 不同的列可以出自同一个域,不同的属性要有不同的属性名
- 列的顺序无所谓。
- 任意两个元组的候选码不能取相同的值。
- 行的顺序无所谓。
- 分量必须取原子值,每一个分量都不可分。
关系模式

或者表示为R(U,D,DOM,F)
R:关系名。
U:组成该关系的属性名的集合。
D: U中的属性所来自的域。
DOM:属性向域的映像集合。
F:属性见数据的依赖关系集合。
关系是关系模式在某一时刻的状态或内容
关系模式是静态的、稳定的,而关系是动态的,随时间不断变化的。
关系数据库
关系数据库的型就是关系数据库模式
关系数据库的值就是关系数据库模式在某一时刻对应的关系的集合
2.2关系操作
特点:集合操作方式,操作对象和结果都是集合
也称为一次一集合的方式,非关系数据库模型的操作方式则成为一次记录的方式
关系数据语言的分类
- 代数方式:关系代数,用关系的运算来表达查询要求
- 逻辑方式:关系演算,用谓词来表达查询要求
- 元组关系演算
- 域关系演算
以上三种方式在表达能力上是等价的,都具有完备的表达能力;它们是抽象的查询语言。与实际的查询语言并不完全一样,但它们能用作评估实际系统中查询语言能力的标准或基础
- 具有关系代数和关系演算双重特点的语言:SQL(Structured Query Language)
SQL是集查询(DQL),数据定义语言(DDL),数据操纵语言(DML)和数据控制语言(DCL)于一体的关系 数据语言
2.3关系的完整性
关系模型中有三类完整性约束:实体完整性,参照完整性和用户定义完整性。
前两个是关系模型必须满足的
实体完整性
若属性A是基本关系R的主属性,那么A不能取空值。
参照完整性
若属性或属性组F是关系R的外码, 它与基本关系S的主码K相对应,则对于R中的每个元组在F上的值必须:
- 或者等于空值(F的每个属性均为空)。
- 或者等于S中某个元组的主码值。
用户定义完整性
用户自定义完整性是针对某一具体关系数据库的约束条件,它反映某一具体应用所涉及的数据必须满足的语义要求。 主要包括非空约束、唯一约束、检查约束、主键约束、外键约束。
2.4 关系代数
关系代数是一种抽象的查询语言,他用对关系的运算来表达查询
三要素: 运算对象(一种关系),运算符,运算结果(一种关系)
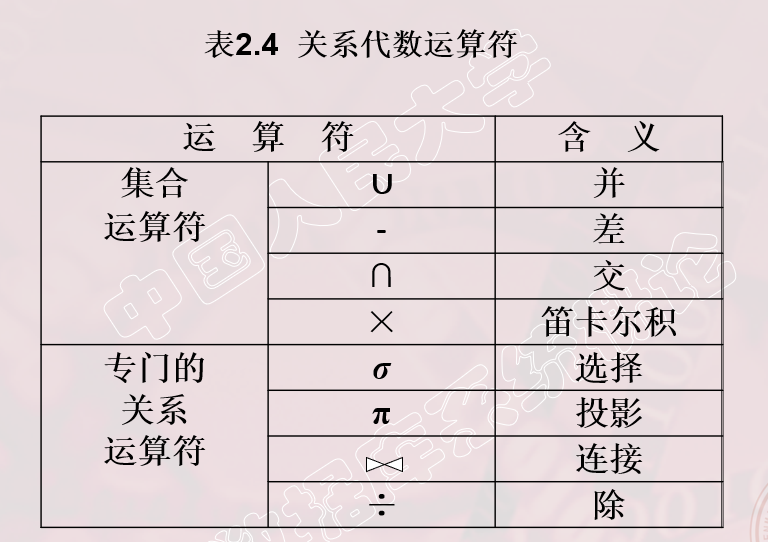
传统的集合运算
并(Union)
R和S
具有相同的目n(即两个关系都有n个属性)
相应的属性取自同一个域
R∪S
仍为n目关系,由属于R或属于S的元组组成
R∪S={t∣t∈R∨t∈S}R∪S = \{ t|t \in R∨t \in S \} R∪S={t∣t∈R∨t∈S}
差(difference)
R和S
具有相同的目n
相应的属性取自同一个域
R - S
仍为n目关系,由属于R而不属于S的所有元组组成
R−S={t∣t∈R∧t∉S}R -S = \{ t|t\in R∧t \notin S \} R−S={t∣t∈R∧t∈/S}
交(intersection)
R和S
具有相同的目n
相应的属性取自同一个域
R∩S
仍为n目关系,由既属于R又属于S的元组组成
R∩S={t∣t∈R∧t∈S}R∩S=R–(R−S)R∩S = \{ t|t \in R∧t \in S \} \\ R∩S = R –(R-S) R∩S={t∣t∈R∧t∈S}R∩S=R–(R−S)
笛卡尔积
严格地讲应该是广义的笛卡尔积(Extended Cartesian Product)
R: n目关系,k 1 个元组
S: m目关系,k2 个元组
R×S
列:(n+m)列元组的集合
元组的前n列是关系R的一个元组
后m列是关系S的一个元组
行:k1 × k2 个元组
R×S={trts^∣tr∈R∧ts∈S}R×S = \{\widehat{tr \ ts} |tr \in R ∧ ts \in S \} R×S={tr ts∣tr∈R∧ts∈S}
专门的关系符运算
选择(selection)

关系代数中<> 表示不等于
投影(project)

如果有重复的,要去掉
连接(join)
也称为θ-连接

DBMS在进行连接操作的时候,不会先生成笛卡尔积,因此效率更高
对自身的连接,要用到更名

等值连接
当θ为“=” 时,称为等值连接
自然连接
自然连接是一种特殊的等值连接

在自然连接中被舍弃的元组被称为悬浮元组
外连接
如果把悬浮元组保留在结果关系中,而在其他属性上填空值null,那么这种链接就叫做外连接

除(divide)

S 可以有R没有的属性
R ÷ S 和 S 的笛卡尔积 是 R 和S 自然连接 的子集
2.5关系演算
关系元组演算

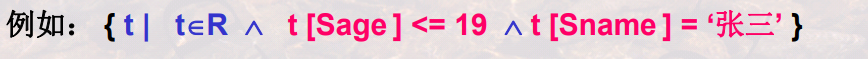
关系域演算


相关文章:

【数据库】第二章 关系数据库
第二章 关系数据库 2.1关系数据结构及形式化定义 关系 域(domain) :域是一组具有相同数据类型的值的集合,可以取值的个数叫基数 笛卡尔积 :一个记录叫做一个元组(tuple),元组中每一个属性值,叫一个分量 基数&…...

oracle和mysql的分页
oracle的分页:rownum 注意:: 对 ROWNUM 只能使用 < 或 <, 用 、 >、 > 都不能返回任何数据。 rownum是对结果集的编序排列,始终是从1开始,所以rownum直接使用时不允许使用>、> 所以当查询中间部分的信息时&…...

深拷贝与浅拷贝的理解
浅拷贝的理解浅拷贝的话只会拷贝基本数据类型,例如像string、Number等这些,类似:Object、Array 这类的话拷贝的就是对象的一个指针(通俗来讲就是拷贝一个引用地址,指向的是一个内存同一份数据),也就是说当拷贝的对象数…...

Shell变量
一、变量分类 根据作用域分三种 (一)只在函数内有效,叫局部变量 (二)只在当前shell进程中有效,叫做全局变量 (三)在当前shell进程与子进程中都有效,叫做环境变量 shell进…...
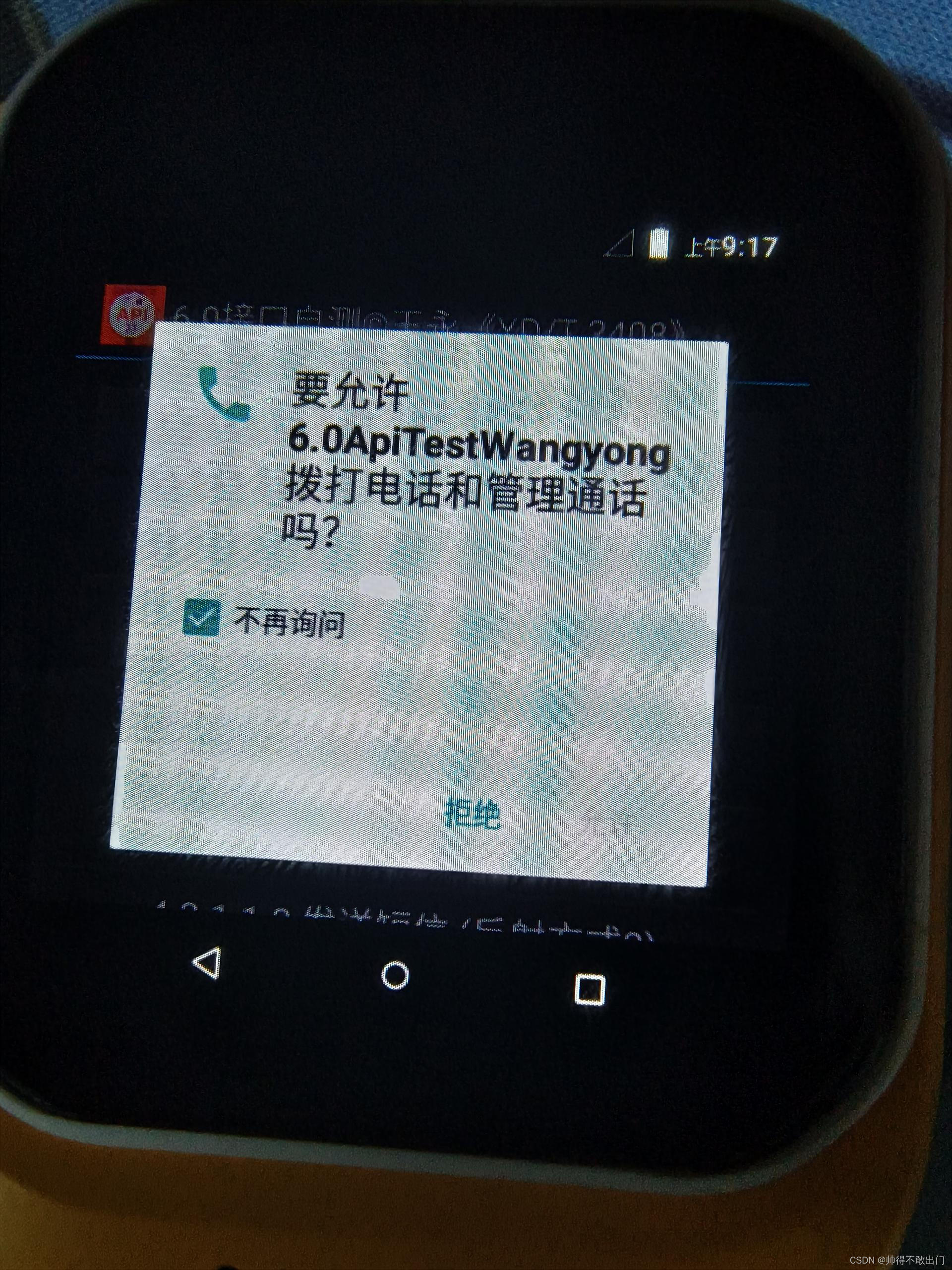
Android 8请求权限时弹窗BUG
弹窗BUG 应用使用requestPermissions申请权限时,系统会弹出一个选择窗口,可进行允许或拒绝, 此窗口中有一个”不再询问“的选择框, ”拒绝”及“允许”的按钮。 遇到一个Bug,单点击“不再询问”,“允许”这个按钮会变…...

路漫漫:网络空间的监管趋势
网络空间是“以相互依存的网络基础设施为基本架构,以代码、信息与数据的流动为环境,人类利用信息通讯技术与应用开展活动,并与其他空间高度融合与互动的空间”。随着信息化技术的发展,网络空间日益演绎成为与现实人类生存空间并存…...

洛谷 P1208 [USACO1.3]混合牛奶 Mixing Milk
最后水一篇水题题解(实在太水了) # [USACO1.3]混合牛奶 Mixing Milk ## 题目描述 由于乳制品产业利润很低,所以降低原材料(牛奶)价格就变得十分重要。帮助 Marry 乳业找到最优的牛奶采购方案。 Marry 乳业从一些奶农手…...

数据库的基本查询
注意:LIMIT的两个参数,第一个是起始位置,第二个是一次查询到多少页。注意:什么类型的数字都是可以排序的。日期的降序是从现在到以前,MySQL ENUM值如何排序?在MYSQL中,我们知道每个ENUM值都与一…...
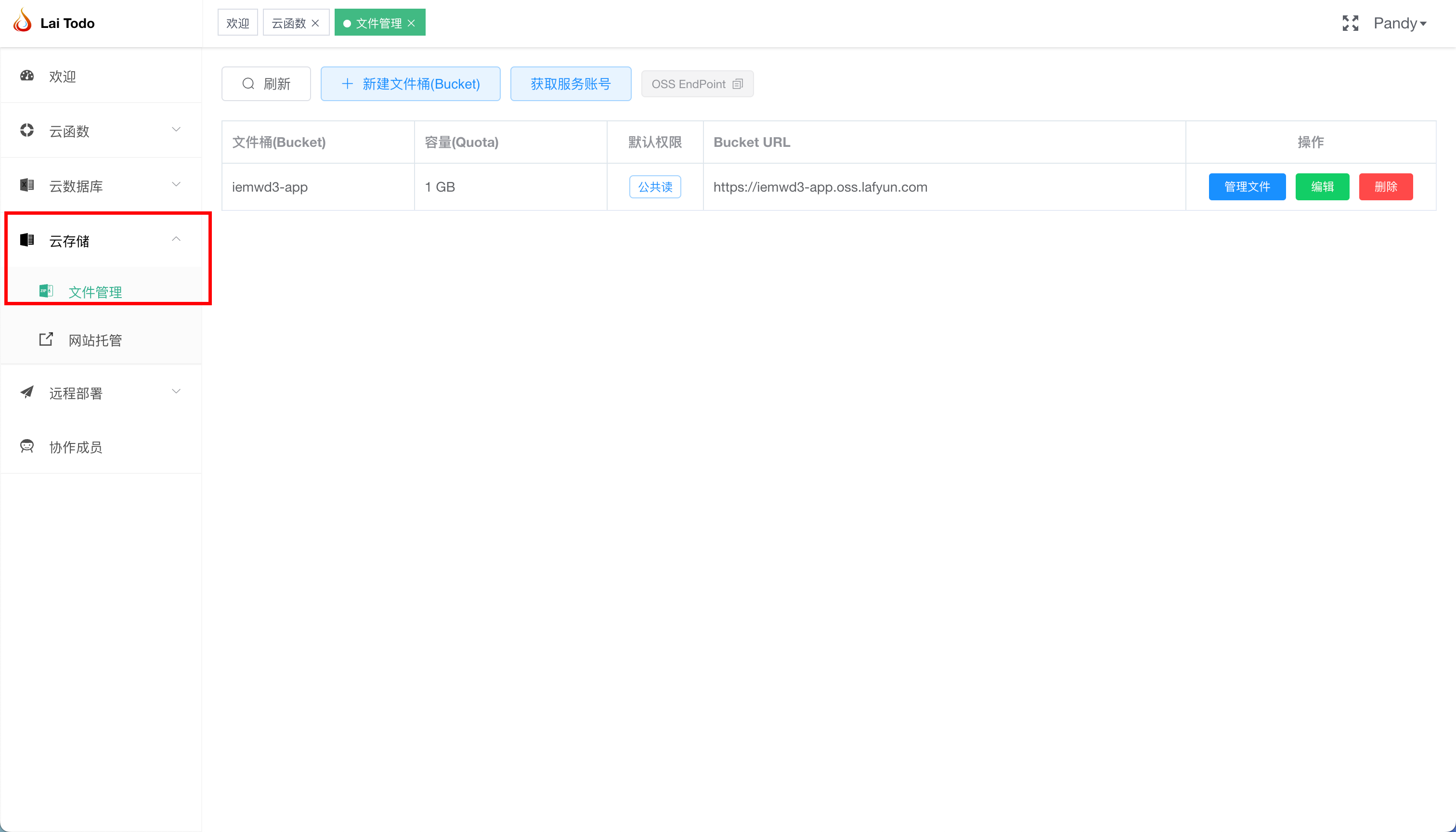
10 分钟把你的 Web 应用转为桌面端应用
在桌面端应用上,Electron 也早已做大做强,GitHub桌面端、VSCode、Figma、Notion、飞书、剪映、得物都基于此。但最近后起之秀的 Tauri 也引人注目,它解决了 Electron 一个大的痛点——打包产物特别大。 我们知道 Electron 基于谷歌内核 Chro…...
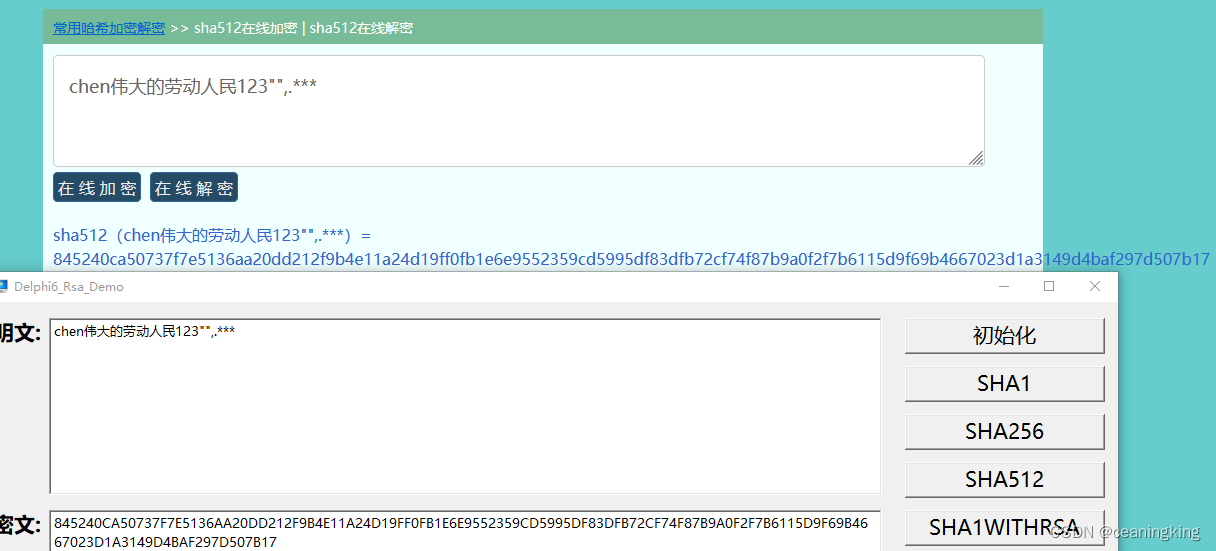
Delphi RSA加解密(二)
dll开发环境: Delphi XE 10.1 Berlin exe开发环境: Delphi 6 前提文章: Delphi RSA加解密(一) 目录 1. 概述 2. 准备工作 2.1 下载DEMO程序 2.2 字符编码说明 3. Cryption.dll封装 3.1 接口概况 3.2 uPub.pas单元代码 3.3 uInterface.pas单元代码 3.4 特别注意 4. 主程序…...

pytorch 深度学习早停设置
当你设置早停的时候你需要注意的是你可能得在几个epoch后才开始判断早停。 早停参数设置 早停(Early Stopping)是一种常用的防止深度学习模型过拟合的方法。早停的设置需要根据具体情况进行调整,常见的做法是在模型训练过程中使用验证集&am…...
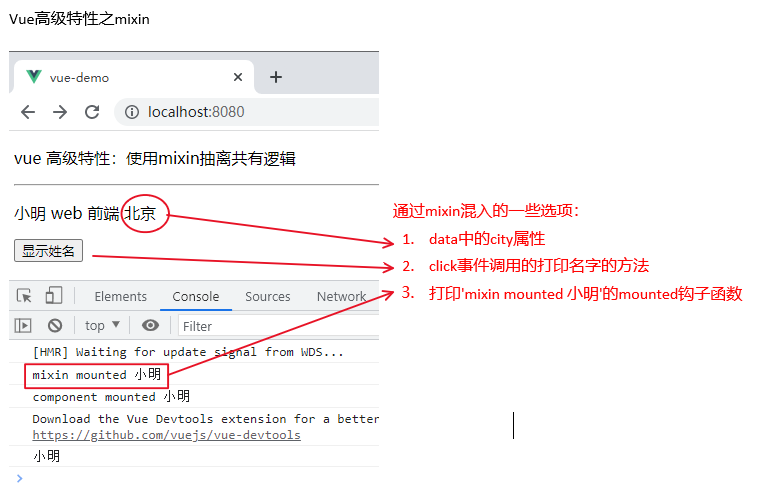
【Vue学习】Vue高级特性
1. 自定义v-model Vue中的自定义v-model指的是在自定义组件中使用v-model语法糖来实现双向绑定。在Vue中,通过v-model指令可以将表单元素的值与组件实例的数据进行双向绑定。但是对于自定义组件,如果要实现v-model的双向绑定,就需要自定义v-…...

Android 12.0 系统Settings去掉开发者模式功能
1.概述 在12.0的系统rom产品定制化开发中,在系统Settings中的关于手机的选项中,系统默认点击版本号5次会自动打开开发者模式,但是在某些产品开发过程中,禁止打开开发者模式,需要去掉开发者模式的功能,所以需要在系统Settings中查看开发者模式的相关流程代码,然后禁用掉开…...
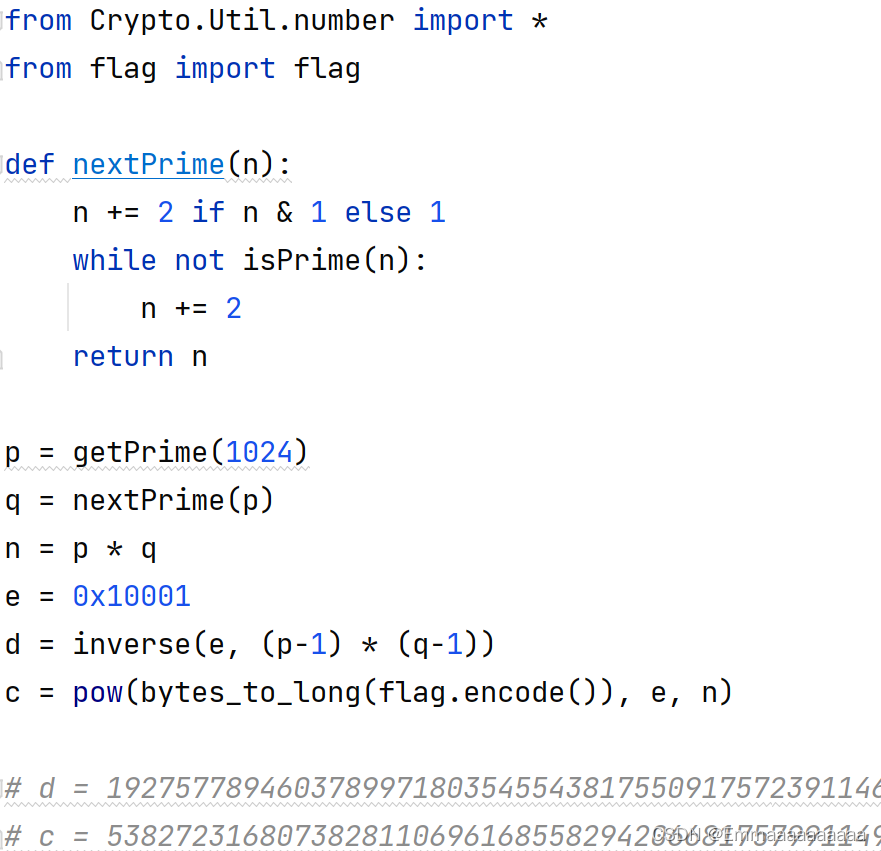
buu [NCTF2019]babyRSA 1
题目描述: 题目分析: 首先明确两个公式: e*d 1 mod (p-1)(q-1) ed1 e*d - 1 k(p-1)(q-1)想要解出此题,我们必须知道n,而要知道n,我们要知道p和q的值通过 e*d 的计算,我们知道其长度为2066位,而生成p的…...

Java:如何选择一个Java API框架
Java编程语言是一种高级的、面向对象的语言,它使开发人员能够创建健壮的、可重用的代码。Java以其可移植性和平台独立性而闻名,这意味着Java代码可以在任何支持Java运行时环境(JRE)的系统上运行。Java和Node js一样,是一种功能强大的通用编程…...

mt6735 MIC 音量的调整及原理介绍
[DESCRIPTION] MIC 音量的调整及原理介绍[SOLUTION] audio_ver1_volume_custom_default.h#define VER1_AUD_VOLUME_MIC \ 64,112,192,144,192,192,184,184,184,184,184,0,0,0,0,\ 255,192,192,180,192,192,196,184,184,184,184,0,0,0,0,\ 255,208,208,180,255,208,196,0,0,0,0,…...
【深度学习】什么是线性回归逻辑回归单层神经元的缺陷
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录逻辑回归&线性回归单层神经元的缺陷单层神经元的缺陷逻辑回归&线性回归 线性回归预测的是一个连续值, 逻辑回归给出的”是”和“否”的回答. 等…...
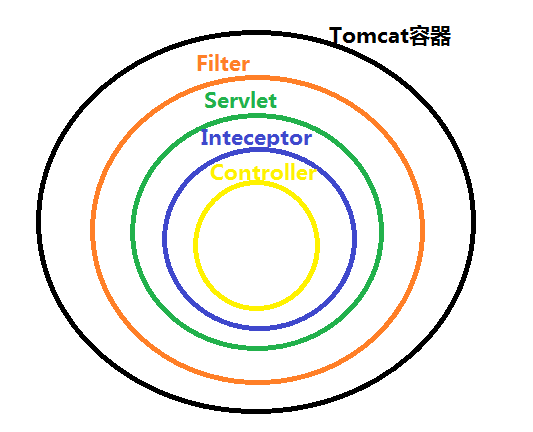
Spring拦截器
SpringMVC提供了拦截器机制,允许运行目标方法之前进行一些拦截工作或者目标方法运行之后进行一下其他相关的处理。自定义的拦截器必须实现HandlerInterceptor接口。preHandle():这个方法在业务处理器处理请求之前被调用,在该方法中对用户请求…...

8个可能降低网站搜索引擎信任度的错误
如果觉得文章对你有用请点赞与关注,每一份支持都是我坚持更新更优质内容的动力!!!例如,发布一段质量差的网站内容不会完全破坏您的排名机会,只要您的内容策略的其余部分井井有条。但是本地SEO中存在一些错误…...

弱监督论文阅读:P2BNet算法笔记
标题:Point-to-Box Network for Accurate Object Detection via Single Point Supervision 会议:ECCV2022 论文地址:https://link.springer.com/10.1007/978-3-031-20077-9_4 官方代码:http://www.github.com/ucas-vg/P2BNet 作者…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...