32二叉树——DFS深度优先遍历
目录
深度优先算法(Depth-First Search,DFS)
LeetCode之路——102. 二叉树的层序遍历
分析

深度优先算法(Depth-First Search,DFS)
DFS是一种用于遍历或搜索树状数据结构的算法,其中它首先探索树的深度,然后回溯并继续探索其他分支。在二叉树中,深度优先算法可以通过递归或使用栈来实现。有三种常见的深度优先遍历方式:前序遍历、中序遍历和后序遍历,每种方式都对节点的访问顺序略有不同。
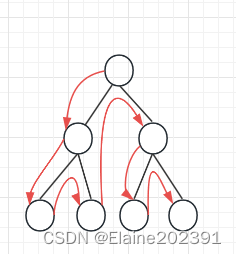
以下是深度优先遍历的Java代码示例,包括前序遍历、中序遍历和后序遍历:
class TreeNode {int data;TreeNode left;TreeNode right;
public TreeNode(int data) {this.data = data;}
}
// 前序遍历(Preorder DFS)
void preorderDFS(TreeNode node) {if (node == null) return;System.out.print(node.data + " "); // 先访问根节点preorderDFS(node.left); // 遍历左子树preorderDFS(node.right); // 遍历右子树
}
// 中序遍历(Inorder DFS)
void inorderDFS(TreeNode node) {if (node == null) return;inorderDFS(node.left); // 遍历左子树System.out.print(node.data + " "); // 访问根节点inorderDFS(node.right); // 遍历右子树
}
// 后序遍历(Postorder DFS)
void postorderDFS(TreeNode node) {if (node == null) return;postorderDFS(node.left); // 遍历左子树postorderDFS(node.right); // 遍历右子树System.out.print(node.data + " "); // 最后访问根节点
}
LeetCode之路——102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
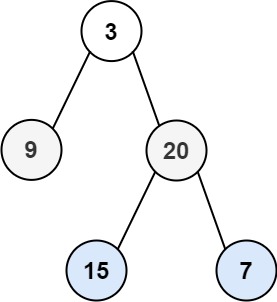
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1] 输出:[[1]]
示例 3:
输入:root = [] 输出:[]
提示:
-
树中节点数目在范围
[0, 2000]内 -
-1000 <= Node.val <= 1000
分析
逐层地,从左到右访问所有节点,这种情景叫做树的层序遍历。匹配的算法是DFS(Depth-first search)和BFS(Breadth-first search)。
// DFS算法-前序遍历
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> resList = new ArrayList<List<Integer>>();dfsPreorder(root, 0, resList);return resList;}/*** 前序遍历的DFS* @param node* @param deep*/public static void dfsPreorder(TreeNode node, int deep, List<List<Integer>> resList) {if (node == null) return;deep++;
if (resList.size() < deep) {// 用resList的索引标记层数List<Integer> list = new ArrayList<>();resList.add(list);}resList.get(deep - 1).add(node.val);
//左侧子节点遍历dfsPreorder(node.left, deep, resList);//右侧子节点遍历dfsPreorder(node.right, deep, resList);}}
-
时间复杂度:O(n)
-
空间复杂度:O(n)
相关文章:

32二叉树——DFS深度优先遍历
目录 深度优先算法(Depth-First Search,DFS) LeetCode之路——102. 二叉树的层序遍历 分析 深度优先算法(Depth-First Search,DFS) DFS是一种用于遍历或搜索树状数据结构的算法,其中它首先探…...
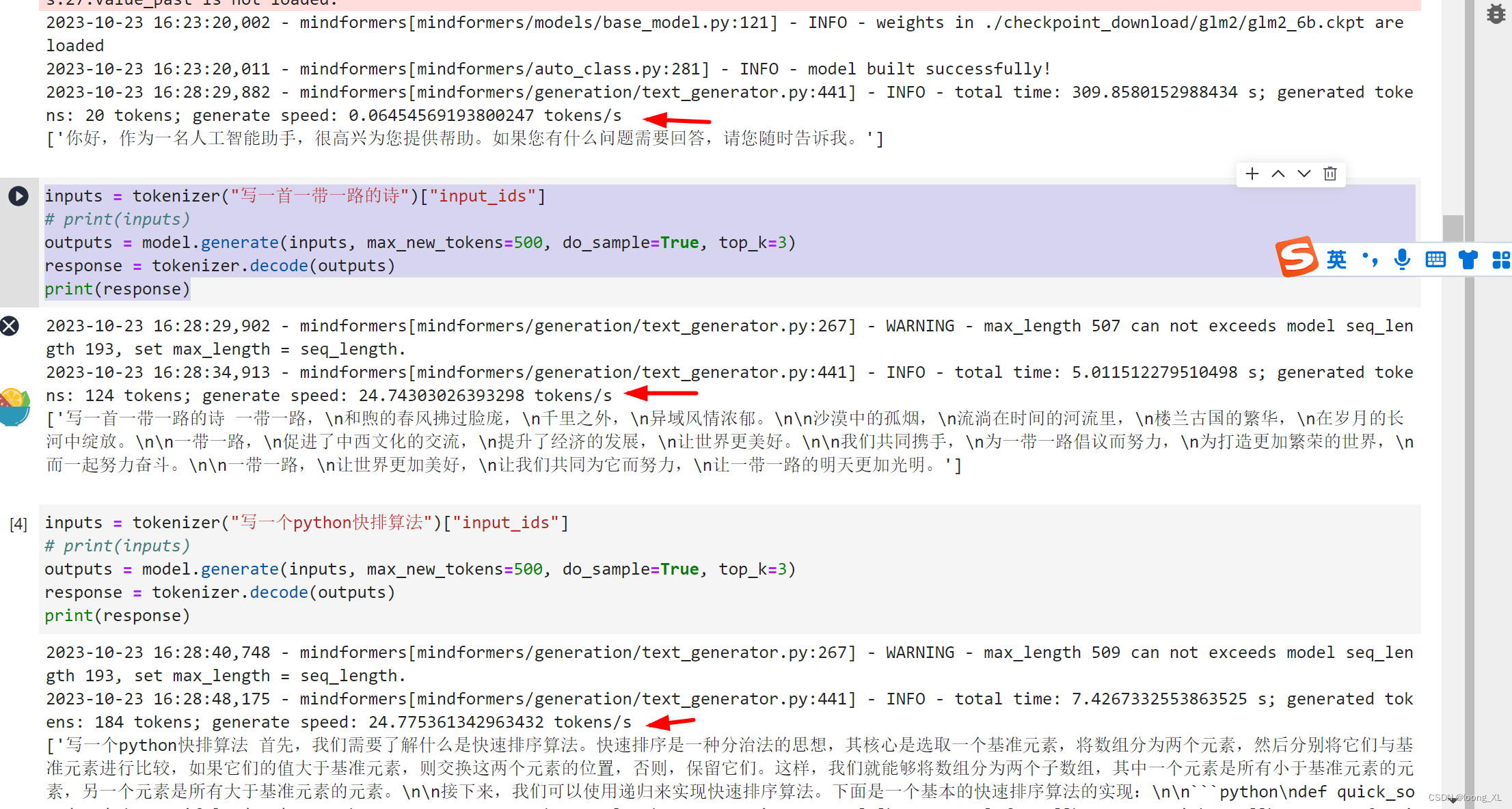
华为昇腾NPU卡 ChatGLM2模型使用
参考:https://gitee.com/mindspore/mindformers/blob/dev/docs/model_cards/glm2.md#chatglm2-6b 1、安装环境: 昇腾NPU卡对应英伟达GPU卡,CANN对应CUDA底层; mindspore对应pytorch;mindformers对应transformers 本…...
【机器学习】集成模型/集成学习:多个模型相结合实现更好的预测
1. 概述 1.1 什么是集成模型/集成学习 "模型集成"和"集成学习"是相同的概念。它们都指的是将多个机器学习模型组合在一起,以提高预测的准确性和稳定性的技术。通过结合多个模型的预测结果,集成学习可以减少单个模型的偏差和方差&am…...

如何提高广告投放转化率?Share Creators 资产库与Appsflyer营销数据的全面结合
如何提高广告投放转化率?Share Creators 资产库与Appsflyer营销数据的全面结合 全球经济进入了低迷期。 营销成本越来越高, 营销需要更务实,注重投入产出比。众所周知,除了渠道、客群画像以外, 优秀的广告设计图&#…...
《软件方法》2023版第1章(11)1.4.3 具体工作步骤
DDD领域驱动设计批评文集 做强化自测题获得“软件方法建模师”称号 《软件方法》各章合集 1.4 应用UML的建模工作流 1.4.3 使用UML建模的工作流步骤 图1-17中“工件形式”一列所列出的图就是本书推荐的在建模工作流ABCD中的UML用法,我用活动图进一步表示建模的步…...

git将当前分支A强制推送远程分支pro上
前言 开发中基于线上分支pro创建了A分支,开发完成之后。又基于线上分支pro创建了B分支,都以此合并到测试分支,两个分支更改中都动用部分共同的文件,这就导致后续开发合并代码越来越乱,这时你想把本地开发的分支强推到…...

【计算机基础】存储器
目录 一.概念二.分类1.按存储介质分类2.按存储方式分类3.按存储器的读写功能分类4.按信息的可保存性分类5.按在计算机系统中的作用分类 三.主存区分SRAM、DRAM、Flash、DDR1.SRAM(静态随机存储器࿰…...

【LCR 159. 库存管理 III】
目录 一、题目描述二、算法原理三、代码实现 一、题目描述 二、算法原理 三、代码实现 class Solution { public:int getrandom(int left,int right,vector<int>& stock){return stock[rand()%(right-left1)left];}void qsort(int l,int r,vector<int>& s…...

Android ADB 常见问题和注意事项
Android ADB 常见问题和注意事项 在使用 ADB 过程中,可能会遇到一些常见问题和需要注意的事项: 1. USB 调试 要使用 ADB,你需要在设备上启用 USB 调试模式。这通常在设备的开发者选项中设置。如果你不能看到开发者选项,可以在设…...
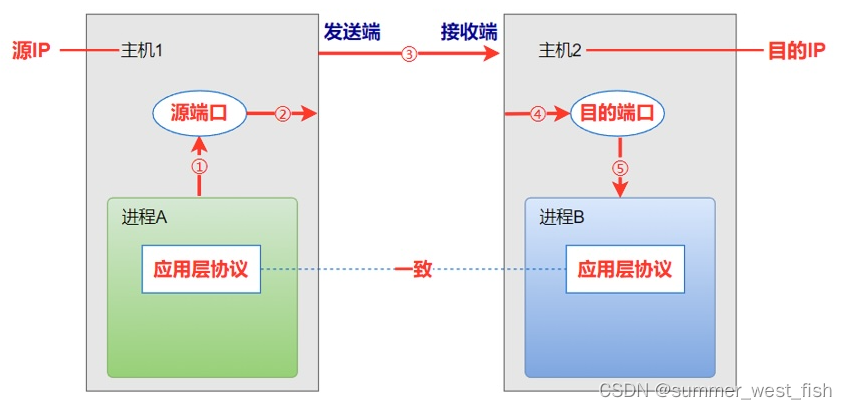
TCP/IP五元组
什么是五元组规则? 五元组是通信术语,英文名称为five-tuple,或5-tuple,五元组包括源IP地址(source IP)、源端口(source port)、目的IP地址(destination IP)、目的端口(destination port) 和 传输层协议(the layer 4 protocol)的五个量集合。…...

aiohttp ssl.SSLError: [SSL: SSLV3_ALERT_HANDSHAKE_FAILURE] 错误处理
这个问题原因吧其实就是3.10 开始官网更新了TLS 堆栈默认安全设置 感兴趣的可以看下链接 python官网叙述: Python 3.10 增加了 TLS 堆栈的默认安全设置 解决也很简单,将ssl安全等级降下来就行,例如: import ssl import aiohttp ctx ssl.cr…...
分析RPA流程自动化的挑战和解决方案
随着数字化工具和自动化解决方案的日益成熟,各行各业发掘到RPA机器人流程自动化技术的先进性,逐渐规模化部署RPA。 为了更好地推进RPA的实施,金智维在这里分享一些运用这项技术时面临的共同挑战,并给出针对性的解决方案。 组织架构…...
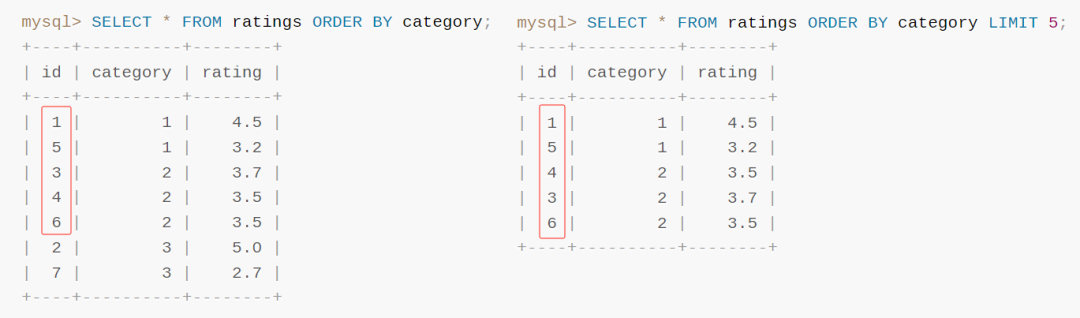
我试图扯掉这条 SQL 的底裤。只能扯一点点,不能扯多了
之前不是写分页嘛,分页肯定就要说到 limit 关键字嘛。 然后我啪的一下扔了一个链接出来: https://dev.mysql.com/doc/refman/8.0/en/limit-optimization.html 这个链接就是 MySQL 官方文档,这一章节叫做“对 Limit 查询的优化”,针对 limit 和 order by 组合的场景进行了较…...

LeNet(pytorch实现
LeNet 本文编写了一个简单易懂的LeNet网络,并在F-MNIST数据集上进行测试,允许使用GPU计算 在这里插入代码片 import torch from torch import nn, optim import d2lzh_pytorch as d2ldevice torch.device(cuda if torch.cuda.is_available() else cp…...

Selenium获取百度百科旅游景点的InfoBox消息盒
前面我讲述过如何通过BeautifulSoup获取维基百科的消息盒,同样可以通过Spider获取网站内容,最近学习了SeleniumPhantomjs后,准备利用它们获取百度百科的旅游景点消息盒(InfoBox),这也是毕业设计实体对齐和属…...
springcloud笔记 (8) -网关 Gateway
网关 出国需要过海关 网关:网络的关卡 网关的作用 1:路由转发 2:安全控制 保护每个服务,不需要将每个暴露出去 3:负载均衡 1.没有网关:客户端直接访问我们的微服务,会需要在客户端配置很多…...

【C++编程语言】STL常用算法 算术生成和集合算法
1.算术生成算法概念 算法简介: accumlate 计算容器元素累计总和fill 向容器中添加元素 注意:算术生成算法属于小型算法 使用时包含头文件为#include<numeric> 2.accumulate /*函数原型:int accumulate(iterator beg ,iterator end…...

解放双手:VMLogin自动化工具的高效便捷
在现代工作环境中,时间和效率是我们追求的关键。幸运的是,随着技术的发展,自动化工具为我们提供了解放双手的机会。其中,防关联浏览器的自动化就是一种强大的工具,能够简化我们的工作流程并提升效率。本文将探讨浏览器…...

深度解析网络代理技术及其在网络安全和爬虫应用中的关键作用
在当今数字化时代,网络代理技术在维护网络安全、保护隐私以及实现高效数据获取方面发挥着不可或缺的作用。本文将全面解析Socks5代理、IP代理等关键技术,并探讨其在网络安全和爬虫开发中的重要作用。 1. Socks5代理与SK5代理:多功能代理协议…...
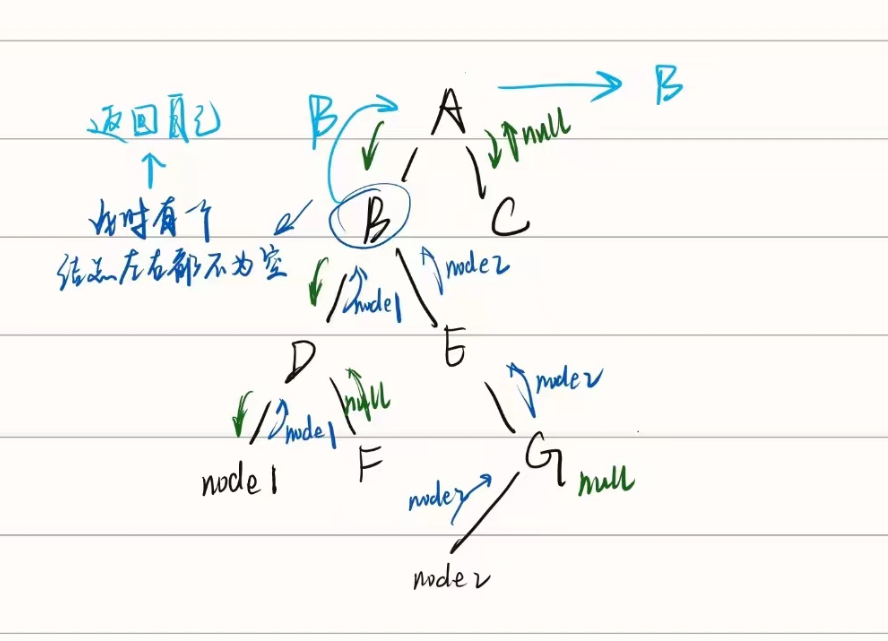
寻找二叉树的最低公共祖先节点
两个节点沿二叉树向上找,找到的第一个公共的节点 例:D和F之间的最低公共节点:B D → B; F → E → B; E和G最低公共节点:A E → B → A; G → C → A; B和F最低公共节点ÿ…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...
